基于统计方法的语言模型
基于统计方法的语言模型
基于统计方法的语言模型主要是指利用统计学原理和方法来构建的语言模型,这类模型通过分析和学习大量语料库中的语言数据,来预测词、短语或句子出现的概率。
-
N-gram模型:这是最基础的统计语言模型之一,它基于统计语言模型的文本分析算法,用于预测文本中下一个词出现的概率,基于前面出现的n-1个词的序列。N-gram模型的“n”代表序列中元素的数量,常见的有Unigram(N=1)、Bigram(N=2)和Trigram(N=3)模型。
-
隐马尔可夫模型(HMM):这是一种统计模型,基于一个隐藏的马尔可夫链生成不可观测的状态序列,并根据这些隐藏状态产生可观测的序列。HMM通过描述隐藏状态之间的转移概率以及隐藏状态到观测值的发射概率来模拟并预测观测序列的生成过程。
-
最大熵模型:这是一种基于概率分布的模型,用于描述任意语句(字符串)s属于某种语言集合的可能性。
-
条件随机场(CRF):这是一种用于建模序列数据的统计模型,常用于自然语言处理任务,如词性标注和命名实体识别。
N-gram模型
N-gram语言模型是一种基于统计的自然语言处理技术,用于预测文本中连续出现的项目(如字母、音节或单词)的概率。
"N-gram"中的"N"指的是序列中连续项目的数目。
N-gram模型基于一个假设:一个项目的出现只依赖于前面N-1个项目。以下是N-gram模型的一些关键点:
-
Unigram Model(1-gram模型):
- 只考虑单个项目(通常是单词)的概率。
- 忽略了单词之间的上下文关系。
-
Bigram Model(2-gram模型):
- 考虑两个连续项目(通常是单词)的概率。
- 例如,"the"后面跟着"cat"的概率。
-
Trigram Model(3-gram模型):
- 考虑三个连续项目的概率。
- 例如,“the"后面跟着"cat”,然后是"sat"的概率。
-
更高阶的N-gram模型:
- 可以扩展到4-gram、5-gram等,但随着N的增加,模型的复杂度和所需的数据量也会增加。
-
平滑技术:
- 由于N-gram模型依赖于实际观察到的数据,对于未出现过的N-gram序列,模型无法给出概率。为了解决这个问题,需要使用平滑技术,如拉普拉斯平滑(Laplace smoothing)或Good-Turing折扣。
-
交叉熵损失:
- 在训练N-gram模型时,通常使用交叉熵损失函数来衡量模型预测的概率分布与实际观测到的数据之间的差异。
-
局限性:
- 随着N的增加,模型需要更多的数据来覆盖所有可能的N-gram组合,这可能导致数据稀疏问题。
- N-gram模型通常无法捕捉长距离的依赖关系,因为它们只考虑局部的上下文。
N-gram模型计算公式
公式基于条件概率,即给定前N-1个词的情况下,下一个词出现的概率。
P n − grams ( w 1 : N ) = C ( w i − n + 1 : i ) C ( w i − n + 1 : i − 1 ) P_{n-\text{grams}}(w_1:N)=\frac{C(w_{i-n+1}:i)}{C(w_{i-n+1}:i-1)} Pn−grams(w1:N)=C(wi−n+1:i−1)C(wi−n+1:i)
这里:
- C ( w i − n + 1 : i ) C(w_{i-n+1}:i) C(wi−n+1:i)是词序列 w i − n + 1 , w i − n + 2 , … , w i w_{i-n+1},w_{i-n+2},\ldots,w_i wi−n+1,wi−n+2,…,wi在语料库中出现的次数。
- C ( w i − n + 1 : i − 1 ) C(w_{i-n+1}:i-1) C(wi−n+1:i−1)是词序列 w i − n + 1 , w i − n + 2 , … , w i − 1 w_{i-n+1},w_{i-n+2},\ldots,w_{i-1} wi−n+1,wi−n+2,…,wi−1在语料库中出现的次数。
对于Unigram(n=1):
- 分子 C ( w i − 1 + 1 : i ) = C ( w i ) C(w_{i-1+1}:i)=C(w_i) C(wi−1+1:i)=C(wi),即词 w i w_i wi在语料库中出现的次数。
- 分母 C ( w i − 1 + 1 : i − 1 ) = C total C(w_{i-1+1}:i-1)=C_{\text{total}} C(wi−1+1:i−1)=Ctotal,即语料库中词的总数。
对于Bigram(n=2):
- 分子 C ( w i − 2 + 1 : i ) = C ( w i − 1 , w i ) C(w_{i-2+1}:i)=C(w_{i-1},w_i) C(wi−2+1:i)=C(wi−1,wi),即词对 w i − 1 , w i w_{i-1},w_i wi−1,wi在语料库中出现的次数。
- 分母 C ( w i − 2 + 1 : i − 1 ) = C ( w i − 1 ) C(w_{i-2+1}:i-1)=C(w_{i-1}) C(wi−2+1:i−1)=C(wi−1),即词 w i − 1 w_{i-1} wi−1在语料库中出现的次数。
n-grams 的统计学原理
n-grams 语言模型基于马尔可夫假设和离散变量的极大似然估计给出语言符号的
概率。
n 阶马尔可夫假设
N阶马尔可夫假设,也称为N阶马尔可夫链(Markov chain of order N),是马尔可夫过程的一个特例,它描述了一个系统在下一个状态的概率分布仅依赖于当前状态以及之前的N-1个状态。
在自然语言处理中,这个假设被用来构建N-gram模型,其中每个“状态”可以是一个词或者一个字母。
具体来说,N阶马尔可夫假设包含以下几个关键点:
-
状态的依赖性:
- 在一个N阶马尔可夫链中,系统在时间t的状态 X t X_t Xt 仅依赖于时间 t − 1 , t − 2 , . . . , t − N t-1, t-2, ..., t-N t−1,t−2,...,t−N的状态,即 X t − 1 , X t − 2 , … , X t − N X_{t-1}, X_{t-2}, \ldots, X_{t-N} Xt−1,Xt−2,…,Xt−N。
-
条件概率:
- 给定前N个状态,下一个状态的概率是确定的。数学上,这可以表示为:
P ( X t + 1 = x t + 1 ∣ X t = x t , X t − 1 = x t − 1 , … , X t − N = x t − N ) = P ( X t + 1 = x t + 1 ∣ X t = x t ) P(X_{t+1} = x_{t+1} | X_t = x_t, X_{t-1} = x_{t-1}, \ldots, X_{t-N} = x_{t-N}) = P(X_{t+1} = x_{t+1} | X_t = x_t) P(Xt+1=xt+1∣Xt=xt,Xt−1=xt−1,…,Xt−N=xt−N)=P(Xt+1=xt+1∣Xt=xt) - 这意味着,给定当前状态 X t X_t Xt,下一个状态 X t + 1 X_{t+1} Xt+1 的概率分布与之前的状态 X t − 1 , X t − 2 , … , X t − N X_{t-1}, X_{t-2}, \ldots, X_{t-N} Xt−1,Xt−2,…,Xt−N 无关。
- 给定前N个状态,下一个状态的概率是确定的。数学上,这可以表示为:
-
简化的模型:
- 马尔可夫假设通过限制状态之间的依赖关系,简化了模型的复杂度。在语言模型中,这意味着每个词的出现仅依赖于前N-1个词,而不是整个句子的历史。
-
N的选择:
- N的选择取决于具体应用和数据的特性。较小的N值(如1或2)可以减少计算复杂度,但可能无法捕捉足够的上下文信息。较大的N值可以提供更多的上下文信息,但会增加模型的复杂度,并可能导致数据稀疏问题。
-
数据稀疏问题:
- 在高阶马尔可夫模型中,由于可能的状态组合数量急剧增加,很多N-gram组合可能在训练数据中从未出现,导致概率估计为零。这就需要使用平滑技术来估计这些未观察到的状态的概率。
离散型随机变量的极大似然估计(MLE)
离散型随机变量的极大似然估计(MLE)是一种统计学方法,用于估计离散型随机变量的概率分布参数。
核心思想是选择参数值,使得观测到的样本数据出现的概率(似然性)最大。
-
似然函数(Likelihood Function):
- 对于离散型随机变量,似然函数是基于观测样本的联合概率分布,作为参数的函数。如果样本是独立同分布的(i.i.d.),似然函数可以表示为每个观测值概率质量函数(PMF)的乘积。
- 即对于观测值 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn,
似然函数 L ( θ ) L(\theta) L(θ) 为: L ( θ ) = ∏ i = 1 n p ( x i ; θ ) L(\theta) = \prod_{i=1}^{n} p(x_i; \theta) L(θ)=∏i=1np(xi;θ)
其中, p ( x i ; θ ) p(x_i; \theta) p(xi;θ) 是随机变量 X X X 取值为 x i x_i xi 的概率, θ \theta θ 是待估计的参数。
-
对数似然函数(Log-Likelihood Function):
- 由于似然函数的乘积形式可能涉及大量的项,计算不便,通常取似然函数的自然对数,得到对数似然函数:
ℓ ( θ ) = ln L ( θ ) = ∑ i = 1 n ln p ( x i ; θ ) \ell(\theta) = \ln L(\theta) = \sum_{i=1}^{n} \ln p(x_i; \theta) ℓ(θ)=lnL(θ)=∑i=1nlnp(xi;θ)
对数似然函数简化了计算,并且在最大化似然函数时,最大化对数似然函数可以得到相同的结果。
- 由于似然函数的乘积形式可能涉及大量的项,计算不便,通常取似然函数的自然对数,得到对数似然函数:
-
求导和求解:
- 为了找到最大化似然函数的参数值,通常对对数似然函数求导,并令导数等于零求解参数:
d d θ ℓ ( θ ) = 0 \frac{d}{d\theta} \ell(\theta) = 0 dθdℓ(θ)=0
解这个方程可以得到参数的极大似然估计值。
- 为了找到最大化似然函数的参数值,通常对对数似然函数求导,并令导数等于零求解参数:
-
极大似然估计值(MLE):
- 使似然函数或对数似然函数达到最大值的参数 θ \theta θ 称为极大似然估计值,记作 θ ^ \hat{\theta} θ^。这个值代表了在给定样本下,使得观测数据出现概率最大的参数值。
-
性质:
- 极大似然估计具有一些良好的性质,例如一致性(随着样本量的增加,MLE趋于真实参数值)和渐近正态性(对于大样本,MLE的分布趋于正态分布)。
推导
在 n-grams 语言模型中,n 阶马尔可夫假被用来简化真实条件概率的计算。具体来说,对于一个词序列 w 1 , w 2 , . . . , w N {w1, w2, ..., wN} w1,w2,...,wN,第 i 个词 wi 出现的概率只依赖于它前面的 n-1 个词 w i − n + 1 , . . . , w i − 1 {wi-n+1, ..., wi-1} wi−n+1,...,wi−1,即:
P ( w i ∣ w 1 : w i − 1 ) ≈ P ( w i ∣ w i − n + 1 : i − 1 ) P(w_i | w_1:w_{i-1}) \approx P(w_i | w_{i-n+1}:i-1) P(wi∣w1:wi−1)≈P(wi∣wi−n+1:i−1)
这个假设将复杂的条件概率简化为只依赖于最近 n-1 个词的概率,使得计算变得更加可行。
我们使用极大似然估计来近似词序列的条件概率。
给定一个词序列 w 1 , w 2 , . . . , w N {w1, w2, ..., wN} w1,w2,...,wN,其出现的概率可以表示为:
P ( w 1 : N ) = ∏ i = 1 N P ( w i ∣ w 1 : i − 1 ) P(w_1:N) = \prod_{i=1}^{N} P(w_i | w_1:i-1) P(w1:N)=∏i=1NP(wi∣w1:i−1)
根据 n 阶马尔可夫假设,这可以简化为:
P ( w i ∣ w 1 : i − 1 ) ≈ P ( w i ∣ w i − n + 1 : i − 1 ) P(w_i | w_1:i-1) \approx P(w_i | w_{i-n+1}:i-1) P(wi∣w1:i−1)≈P(wi∣wi−n+1:i−1)
然后,我们使用极大似然估计来近似这个条件概率。具体来说,我们用词序列 w i − n + 1 , . . . , w i {w_{i-n+1}, ..., w_i} wi−n+1,...,wi 在语料库中出现的次数 C ( w i − n + 1 : i ) C(w_{i-n+1}:i) C(wi−n+1:i) 除以词序列 w i − n + 1 , . . . , w i − 1 {w_{i-n+1}, ..., w_{i-1}} wi−n+1,...,wi−1 在语料库中出现的次数 C ( w i − n + 1 : i − 1 ) C(w_{i-n+1}:i-1) C(wi−n+1:i−1) 来近似 P ( w i ∣ w i − n + 1 : i − 1 ) P(w_i | w_{i-n+1}:i-1) P(wi∣wi−n+1:i−1):
P ( w i ∣ w i − n + 1 : i − 1 ) ≈ C ( w i − n + 1 : i ) C ( w i − n + 1 : i − 1 ) P(w_i | w_{i-n+1}:i-1) \approx \frac{C(w_{i-n+1}:i)}{C(w_{i-n+1}:i-1)} P(wi∣wi−n+1:i−1)≈C(wi−n+1:i−1)C(wi−n+1:i)
因此,n-grams 语言模型的输出是对真实概率 P(w1:N) 的近似:
P n − g r a m s ( w 1 : N ) ≈ P ( w 1 : N ) P_{n-grams}(w_1:N) \approx P(w_1:N) Pn−grams(w1:N)≈P(w1:N)
这个近似是基于对每个条件概率的极大似然估计,它允许我们根据语料库中词序列的出现频率来估计整个文本序列的概率。
相关文章:

基于统计方法的语言模型
基于统计方法的语言模型 基于统计方法的语言模型主要是指利用统计学原理和方法来构建的语言模型,这类模型通过分析和学习大量语料库中的语言数据,来预测词、短语或句子出现的概率。 N-gram模型:这是最基础的统计语言模型之一,它基…...

Flux comfyui 部署笔记,整合包下载
目录 comfyui启动: 1、下载 Flux 模型 2、Flux 库位置 工作流示例: Flux学习资料免费分享 comfyui启动: # 配置下载模型走镜像站 export HF_ENDPOINT="https://hf-mirror.com" python3 main.py --listen 0.0.0.0 --port 8188 vscode 点击 port 映射到本地,…...

高性能分布式缓存Redis-数据管理与性能提升之道
一、持久化原理 Redis是内存数据库,数据都是存储在内存中,为了避免进程退出导致数据的永久丢失,需要定期将Redis中的数据以某种形式(数据或命令)从内存保存到硬盘;当下次Redis重启时,利用持久化文件实现数据恢复。除此…...

BO-CNN-LSTM回归预测 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多输入单输出回归预测
BO-CNN-LSTM回归预测 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多输入单输出回归预测 目录 BO-CNN-LSTM回归预测 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多输入单输出回归预测效果一览基本介绍模型搭建程序设计参考资料 效果一览 …...

DataWind将字符串数组拆出多行的方法
摘要: 可视化建模中先将字符串split为array再用explode(array)即可 可视化建模 进入“可视化建模”页面 1.1 新建任务 如果团队内没有可视化建模任务。请点击“新建任务”,输入名称并确定。 1.2 建立数据连接 在左边栏中选择“数据连接”,…...

try...catch 和then...catch的异同点分析
try…catch 和 then…catch 的异同点分析 在现代 JavaScript 编程中,异常处理和 Promise 的处理是非常常见的两种方式。try...catch 语句主要用于同步代码的异常处理,而 .then().catch() 是 Promise 中的异步处理方法。 1. 基础概念 1.1 try…catch …...
Mit6.S081-实验环境搭建
Mit6.S081-实验环境搭建 注:大家每次做一些操作的时候觉得不太保险就先把虚拟机克隆一份 前言 qemu(quick emulator):这是一个模拟硬件环境的软件,利用它可以运行我们编译好的操作系统。 准备一个Linux系统…...

以太网交换安全:MAC地址漂移
一、什么是MAC地址漂移? MAC地址漂移是指设备上一个VLAN内有两个端口学习到同一个MAC地址,后学习到的MAC地址表项覆盖原MAC地址表项的现象。 MAC地址漂移的定义与现象 基本定义:MAC地址漂移发生在一个VLAN内的两个不同端口学习到相同的MAC地…...

STM32实现串口接收不定长数据
原理 STM32实现串口接收不定长数据,主要靠的就是串口空闲(idle)中断,此中断的触发条件与接收的字节数无关,只有当Rx引脚无后续数据进入时(串口空闲时),认为这时候代表一个数据包接收完成了&…...

AAA 数据库事务隔离级别及死锁
目录 一、事务的四大特性(ACID) 1. 原子性(atomicity): 2. 一致性(consistency): 3. 隔离性(isolation): 4. 持久性(durability): 二、死锁的产生及解决方法 三、事务的四种隔离级别 0 .封锁协议 …...

外接数据库给streamlit等web APP带来的变化
之前我采用sreamlit制作了一个调查问卷的APP, 又使用MongoDB作为外部数据存储,隐约觉得外部数据库对于web APP具有多方面的意义,代表了web APP发展的趋势之一,似乎是作为对这种趋势的响应,streamlit官方近期开发了st.c…...

Gitpod: 我们正在离开 Kubernetes
原文:Christian Weichel - 2024.10.31 Kubernetes 似乎是构建远程、标准化和自动化开发环境的显而易见选择。我们也曾这样认为,并且花费了六年时间,致力于打造最受欢迎的云开发环境平台,并达到了互联网级的规模。我们的用户数量达…...

1.每日SQL----2024/11/7
题目: 计算用户次日留存率,即用户第二天继续登录的概率 表: iddevice_iddate121382024-05-03232142024-05-09332142024-06-15465432024-08-13523152024-08-13623152024-08-14723152024-08-15832142024-05-09932142024-08-151065432024-08-131123152024-…...
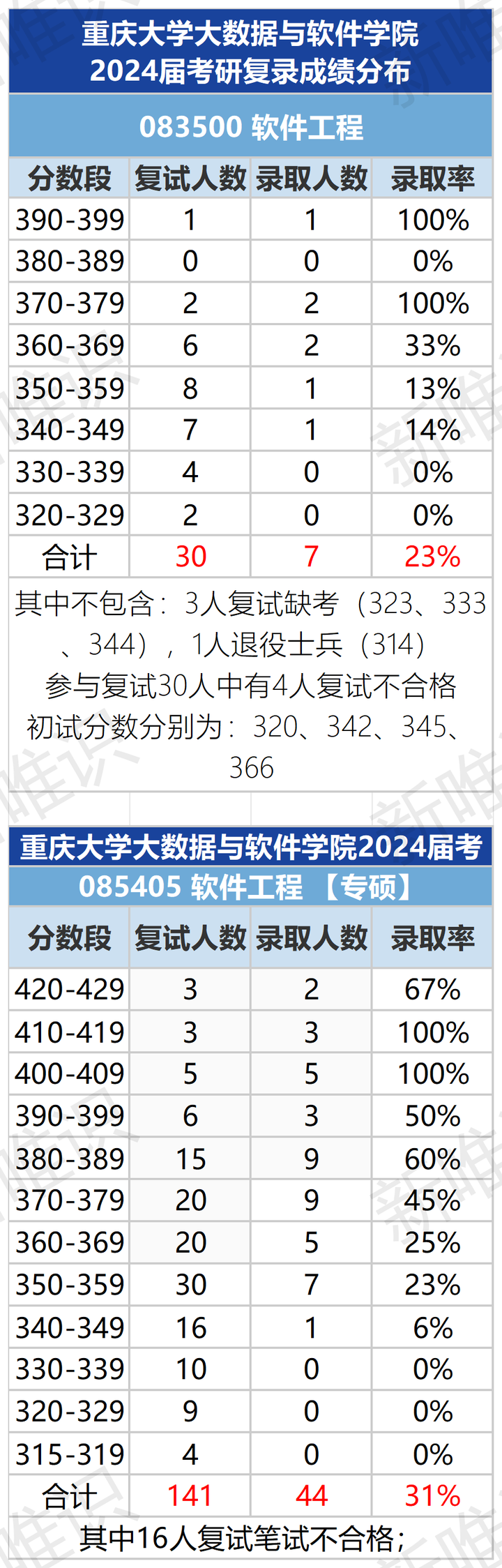
普通一本大二学生,软件工程,想考研985,想知道哪个大学的软件工程好,又不至于完全考不起的?
竞争难度适中:相较于顶尖985院校,重庆大学作为实力派985高校,其竞争烈度较为温和,考研难度适中偏易,为追求高性价比深造路径的考生提供了理想之选。 考试难度友好:重庆地区考研评分标准相对宽松࿰…...

「QT」几何数据类 之 QMatrix4x4 4x4矩阵类
✨博客主页何曾参静谧的博客📌文章专栏「QT」QT5程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasolid…...

让Apache正确处理不同编码的文件避免中文乱码
安装了apache2.4.39以后,默认编码是UTF-8,不管你文件是什么编码,统统按这个来解析,因此 GB2312编码文件内的中文将显示为乱码。 <!doctype html> <html> <head><meta http-equiv"Content-Type" c…...

人员密集场所遇到突发火灾事故该如何应对
0引言 在繁华喧嚣的都市中,人员密集场所如购物中心、电影院、办公楼等,是人们日常生活不可或缺的一部分。然而,在这些看似繁华的背后,隐藏着不可忽视的安全隐患——火灾。火灾无情,往往在不经意间爆发,瞬间…...

使用QtWebEngine的Mac应用如何发布App Store
前言 因为QtWebEngine时第三方包,苹果并不直接支持进行App Store上签名和发布,所以构建和发布一个基于使用QtWebEngine的应用程序并不容易,这里我们对Qt 5.8稍微做一些修改,以便让我们的基于QtWeb引擎的应用程序并让签名能够得到苹果的许可。 QtWebEngine提供了C++和Qml的…...

微机原理与接口技术——中断系统与可编中断控制芯片8259A
目录 一、8259A 芯片介绍 二、8259A 的内部结构和引脚 三、8259A 的中断工作过程 四、8259A 的工作方式 五、8259A 的编程 六、外部中断服务程序 一、8259A 芯片介绍 Intel 8259A 是可编程中断控制器,可用于管理 Intel 8080/8085、8086/8088、80286/80386 的…...

【JavaEE初阶 — 多线程】Thread类的方法&线程生命周期
目录 1. start() (1) start() 的性质 (2) start() 和 Thread类 的关系 2. 终止一个线程 (1)通过共享的标记结束线程 1. 通过共享的标记结束线程 2. 关于 lamda 表达式的“变量捕获” (2) 调用interrupt()方法 1. isInterrupted() 2. currentThread() …...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
