从0开始学习机器学习--Day19--学习曲线
一般来说,如果一个算法的表现不理想,那么多半是因为出现了欠拟合或过拟合问题,这种时候我们要做的就是搞清楚出现的是偏差问题还是方差问题,亦或是二者皆有,这有助于我们精准定位问题所在。
之前,我们发现假设函数多项式的次数越高,代价函数的误差就越小,假设我们把多项式的次数作为横坐标,训练集代价函数的误差为纵坐标画图,呈现出来的应该是随着横坐标增大纵坐标不断减小的图像:

随着多项式次数增加两种代价函数的变化情况
但如果换做是验证集的假设函数,图像又有所不同。可以看到在 的时候,其误差确实小了,这反映的是其预测值和实际值之间的误差变小,但当
时,出现了过拟合的情况,此时预测值与实际值之间的差又变大,所以其曲线又往上升而不是继续下降,这进一步地说明了为什么我们采用验证集的参数而不是直接用训练集的。
也就是说,通过比较训练集和验证集代价函数的误差,可以确定到底是出现了什么问题。假如两者都很大且两者差值较小,则说明式出现了高偏差、欠拟合的情况,应该适当增大多项式的次数;如果训练集的误差远远小于验证集的误差,则说明出现了高方差、过拟合的情况,需要适当减小多项式的次数。
正则化和偏差、方差(Regularization and bias/variance)
在之前学习正则化的时候,我们知道通过正则化参数,可以挑选出不太重要的参数项,从而决定多项式的次数。但之前我们基本默认 ,那么在实际情况中我们该怎么挑选合适的
呢?
假设我们的假设函数是4次项的多项式,我们按从小到大的顺序将不同的带入代价函数算出参数,注意这里的
是按照2倍的速度增长的,当增加到12次时,大概是10.24,这里省略了小数点:

带入不同值计算参数
计算完结果后,再跟上述一样带入到验证集的代价函数中去计算验证集误差,其中误差最小对应的就是我们想要的正则化参数。当然,就算得到了结果,也还是要将在验证集得到的参数带入到测试集的代价函数进行最终验证。
同样的,我们画出训练集代价函数和验证集代价函数关 的图像:

随着增加两种代价函数的变化情况
可以看到,当很大时,此时函数处于欠拟合高偏差的问题中,训练集和验证集的代价函数误差都会很大且很接近;当
很小时,函数处于过拟合、高方差的情况,训练集由于是用自己的数据拟合,拟合的好,误差很小,而验证集的误差则远远大于训练集。一般来说,验证集代价函数的误差最小时,该点的
应该是刚好适合假设函数的正则化参数。
学习曲线(Learning curves)
在上述说法中我们通过对比两种代价函数的误差表现来判断出现什么问题,事实上,我们一般采用画出学习曲线的方式来判断算法的表现好坏,横坐标是训练样本个数,纵坐标是代价函数的误差。但与以往不同,我们对横坐标加以限制,用很少量的样本个数(10,20,30等等)来观察两种代价函数的表现。

两种代价函数误差关于样本个数的图像
假设我们采用二次幂的多项式来拟合,可以观察到,当样本个数很小(1-3)时,曲线会拟合得很好,样本个数到4的时候,能看出曲线已经开始有些偏离了,也就是说,随着样本个数的增加,训练集的代价函数的误差也会随之增大。对于验证集的代价函数来说,在样本个数很小的时候,其误差会很大,原因是其参数的基础只是几个样本,其对于新样本的效果自然很低;当样本个数逐渐增加,算法分析的特征越来也多,意味着其对于新样本的判断能力在逐渐增加,表现在图像上则是验证集代价函数的误差在逐渐减小。

高偏差时两种误差的表现
可以观察到,两种曲线跟刚刚相比也是类似的变化,当样本更加到一定程度时其误差基本保持不变,与其不同的是,由于这里是用直线来拟合,样本个数过大而参数过小,所以当样本个数增加到一定值时,两者的误差基本相等。

高方差时两种误差的表现
如果换成高次幂比如100次方,其曲线与上述相比,训练集的误差在样本数量增加到一定程度后还是基本不变,但验证集的误差则会一直下降,这是因为样本的个数的增加对验证集来说,其由于对数据更敏感相当于接触到了更多的变化来排除原本数据的一些不好的数据(俗称“噪声”),这说明增加样本数量对于高偏差的情况基本没有帮助,但在高方差时表现良好。
在之前,我们总结了一些可能可以改善算法的方法,在这里对这些方法的用途做一个概括。
对于高方差问题来说:
-
增加样本个数,使验证集代价函数感受到更多的变化,使其误差持续减小;
-
减少特征量,让函数专注在有用的特征上,加强拟合效果;
-
增大
,能够增加特征使其拟合效果更好。
对于高偏差问题来说:
-
增加特征量或多项式特征,也就是增加函数的复杂程度,使其更贴合训练样本;
-
减小
,能够减少不必要的特征和“噪声”,减弱过拟合效果。
而在使用神经网络来构建模型时,与之相对的,使用较少的隐藏层和隐藏单元,在架构中所用到的参数就不会很多,会出现欠拟合的现象,其计算量较少;假如用很多隐藏单元或者很多层隐藏层,则会出现过拟合现象,不过我们可以通过加入正则项来解决这个问题(一般为了避免我们会直接添加,而不是等到了出现过拟合再作正则化操作),所以一般越大型、越复杂的神经网络效果越好。
视频参考链接:https://www.bilibili.com/video/BV1By4y1J7A5?spm_id_from=333.788.player.switch&vd_source=867b8ecbd62561f6cb9b4a83a368f691&p=64
相关文章:
从0开始学习机器学习--Day19--学习曲线
一般来说,如果一个算法的表现不理想,那么多半是因为出现了欠拟合或过拟合问题,这种时候我们要做的就是搞清楚出现的是偏差问题还是方差问题,亦或是二者皆有,这有助于我们精准定位问题所在。 之前,我们发现…...

2.索引:深入解析 B+ 树:原理、MySQL 应用及与其他数据结构的对比
B 树是一种高效的平衡树结构,在数据库和文件系统中被广泛应用,尤其在 MySQL 中,InnoDB 存储引擎通过 B 树实现索引结构,提升了大数据量条件下的查询性能。 本文将深入介绍 B 树的原理和设计特点,分析 MySQL 中使用 B …...

[全网最细数据结构完整版]第六篇:3分钟带你吃透栈并模拟实现
目录 1->栈的概念和结构 1.1栈的概念 1.2栈的结构 2->栈的实现 2.1定义关于栈的结构体和各种函数 2.2栈的初始化 STInit 函数 2.3栈的销毁 STDestroy 函数 2.4栈的插入操作 STPush 函数 2.5栈的判断是否为空操作 STEmpty 函数 2.6栈的删除操作 STPop 函数 2.7…...

如何在 Docker 容器中启动 X11 图形界面程序
如何在 Docker 容器中启动 X11 图形界面程序 在使用 Docker 时,我们通常会发现,容器中的图形应用没法直接显示到宿主机的界面上。不过,我们可以通过共享 X11 的 Unix 套接字,让容器把显示数据传递给宿主机的 X11 服务器ÿ…...

pycharm保存是自动格式化
在PyCharm中设置保存时自动格式化代码,可以按照以下步骤进行: 1. 打开设置 在Windows和Linux系统中,可以通过File(文件)->Settings(设置)打开设置窗口;在Mac系统中,…...

.netCore WebAPI中字符串加密与解密
In today’s digital landscape, securing sensitive information is more critical than ever. If you’re using ASP.NET Core, you might store configuration settings in appsettings.json. However, hardcoding sensitive data like connection strings or API keys in p…...

Next.js + Move 石头剪刀布
rock-paper-scissors 写在前面 本地 源码:https://github.com/zcy1024/SuiStudy/tree/main/rock-paper-scissors # 或其它等价的命令来安装依赖并将项目跑起来 pnpm install pnpm run dev # http://localhost:3000/在线(如果没过期的话) …...

[面试]关于Redis 的持久化你了解吗
Redis的持久化是指Redis服务器在关闭或重启时,将内存中的数据保存到磁盘上的一种机制。Redis支持多种持久化方式。 一、RDB(Redis Database)持久化 RDB持久化是Redis默认采用的持久化方式,它将Redis在某个时间点的数据保存到磁盘上…...

Systemd:tmpfiles
Systemd提供了一个结构化的可配置方法来管理临时文件和目录,即systemd-tmpfiles,可以创建、删除和管理临时文件的服务。 $ systemctl list-units --all | grep systemd-tmpfilessystemd-tmpfiles-clean.service load…...

【Flutter 内嵌 android 原生 View以及相互跳转】
Flutter 内嵌 android 原生 View以及相互跳转 一. 内嵌android 原生View二、android 与 flutter 相互跳转 一. 内嵌android 原生View 在android 工程的包名下,也可在MainActivity创建 android 原生view ,继承PlatformView // 1.自定义textview public st…...

python externally-managed-environment 外部管理环境
https://realpython.com/python-virtual-environments-a-primer/?refyaolong.net#why-do-you-need-virtual-environments 简而言之, pip 默认会将您安装的所有外部包放置在 Python 安装路径/site-packages/ 的文件夹中一些Linux 和 macOS操作系统 预装了内部的 P…...
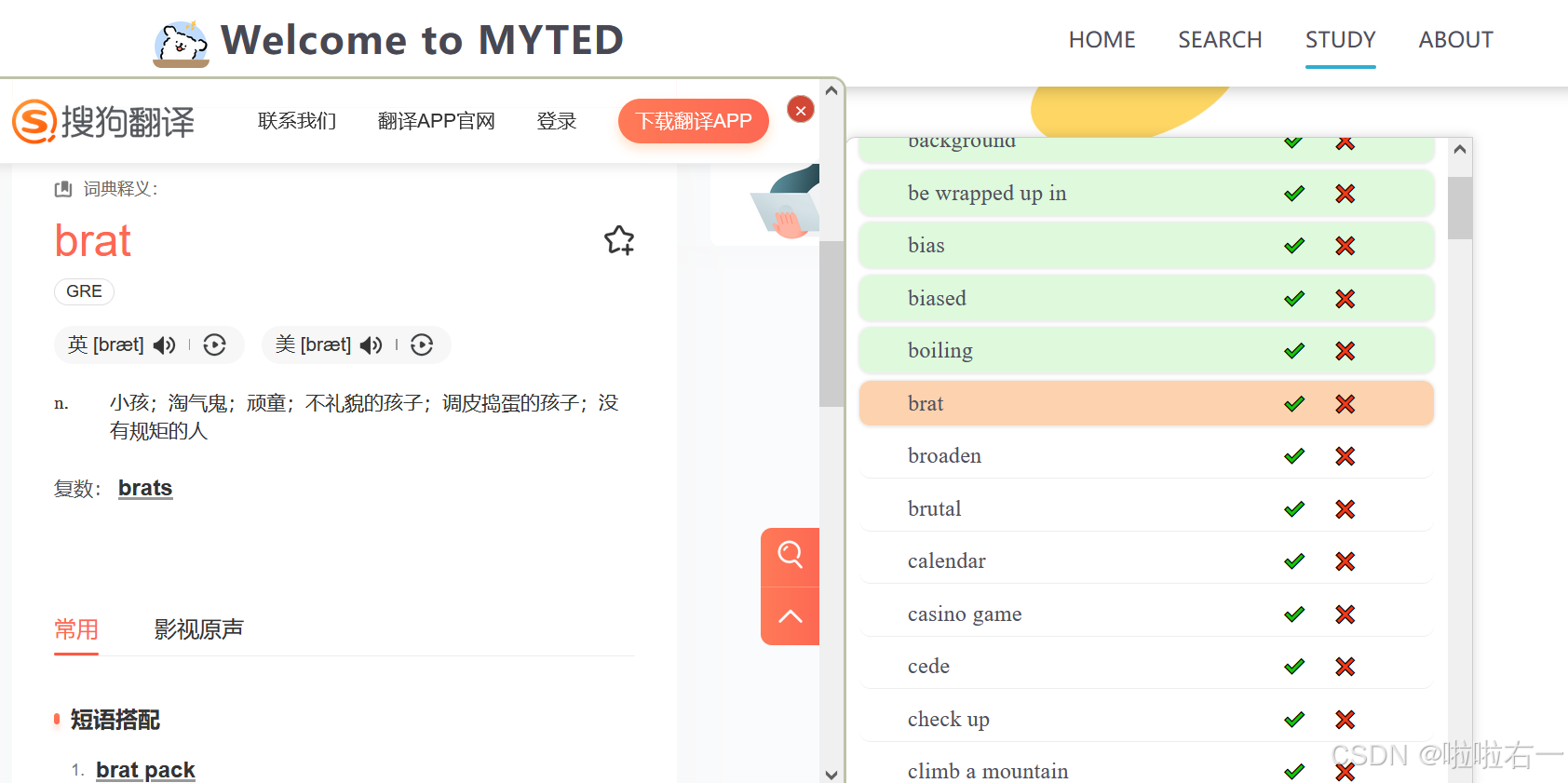
前端 | MYTED单篇TED词汇学习功能优化
文章目录 📚实现效果🐇before🐇after 📚模块实现解析🐇html🐇css🐇javascript 📚实现效果 🐇before 点击TED单篇词汇表按钮,选择对应TED打卡号,…...

64 mysql 的 表锁
前言 我们这里来说的就是 我们在 mysql 这边常见的 几种锁 行共享锁, 行排他锁, 表意向共享锁, 表意向排他锁, 表共享锁, 表排他锁 我们前面了解了行共享锁, 行排他锁, 表意向共享锁, 表意向排他锁 等等相关 我们这里 来看一下 表共享锁, 表排他锁 的获取, 以及 和 其他表级…...
)
【计网不挂科】计算机网络期末考试——【选择题&填空题&判断题&简述题】题库(1)
前言 大家好吖,欢迎来到 YY 滴计算机网络 系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 本博客主要内容,收纳了一部门基本的计算机网络题目,供yy应对期中考试复习。大家可以参考 欢迎订阅 YY滴其他专栏!…...

ajax关于axios库的运用小案例
AJAX案例 图书管理 四大功能: 展示图书删除图书编辑图书信息新增图书 步骤 1.bootstrap弹窗来实现新增和编辑图书时出现的弹窗 有两种方案: a.可以用自带的属性来进行弹窗的显示和隐藏 b.可以通过JS进行控制,此操作可以进行自定义&am…...
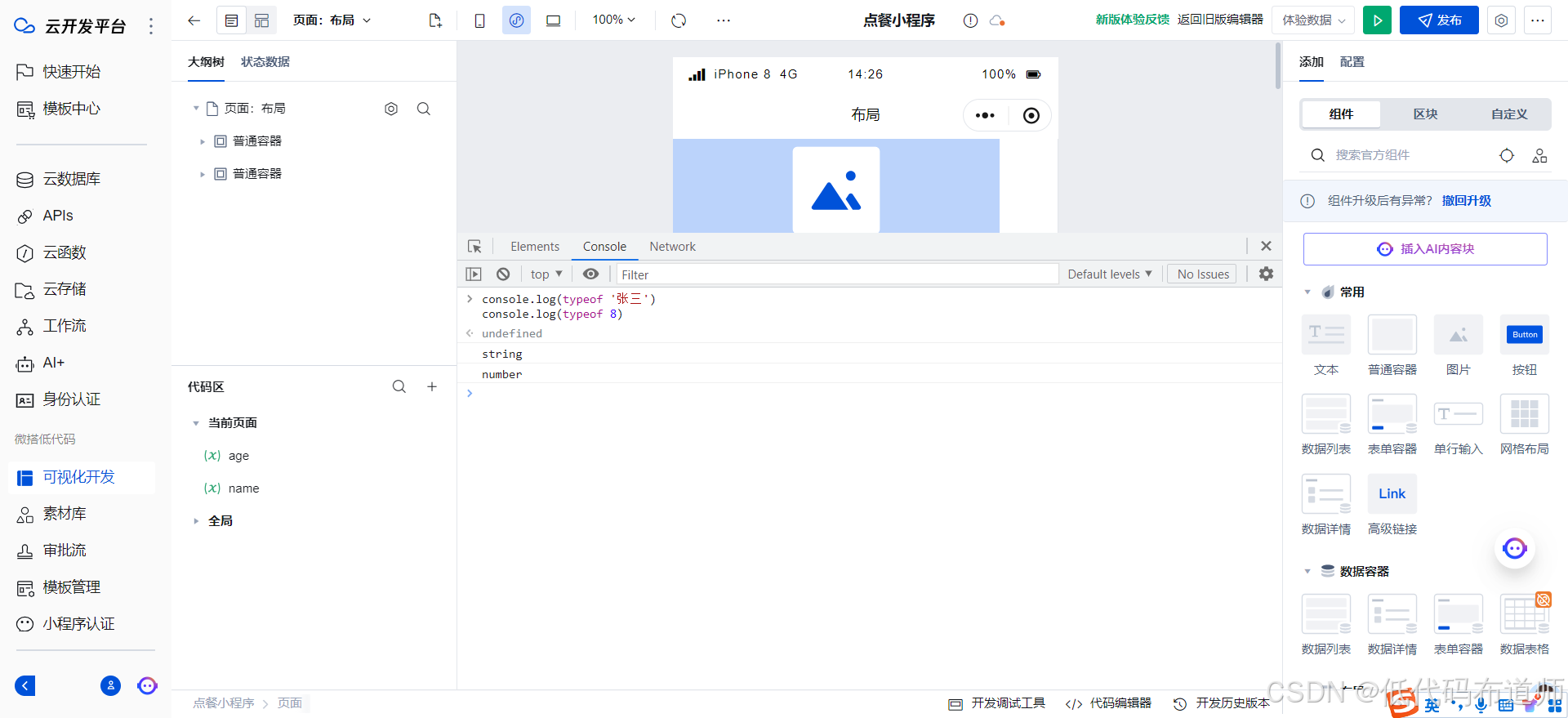
微搭低代码入门01变量
目录 1 变量的定义2 变量的赋值3 变量的类型4 算术运算符5 字符串的连接6 模板字符串7 检查变量的类型8 解构赋值8.1 数组的解构赋值8.2 对象的解构赋值 9 类型转换9.1 转换为字符串9.2 转换为数字9.3 转换为布尔值 总结 好些零基础的同学,在使用低代码的时候&#…...
盘点2024年10款视频剪辑,哪款值得pick!!
在这个短视频盛行的时代,如何让我们的故事更生动有趣呢?那就要对短视频进行修饰了。这就需要借助视频剪辑工具:而一款好的工具不仅仅是视频的“美颜”,更是创意的灵魂所在!想象一下,运用一款功能齐全的剪辑…...
苹果手机照片批量删除:一键清理,释放空间
在数字化时代,iPhone不仅是我们沟通的桥梁,也是记录生活的重要工具。然而,随着时间的积累,手机中的照片数量不断增加,不仅占用大量存储空间,也让设备变得缓慢。苹果手机照片批量删除成为了一个普遍的需求。…...

《AI 大模型:重塑软件开发新生态》
《AI 大模型:重塑软件开发新生态》 一、AI 大模型引领软件开发新潮流二、AI 大模型在软件开发中的优势(一)提高开发效率(二)减少错误与提升质量(三)激发创新与拓展功能 三、AI 大模型在软件开发…...
)
uniapp(API-Promise 化)
一、异步的方法,如果不传入 success、fail、complete 等 callback 参数,将以 Promise 返回数据异步的方法,且有返回对象,如果希望获取返回对象,必须至少传入一项 success、fail、complete 等 callback 参数,…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
