用 Python 从零开始创建神经网络(二)
用 Python 从零开始创建神经网络(二)
- 引言
- 1. Tensors, Arrays and Vectors:
- 2. Dot Product and Vector Addition
- a. Dot Product (点积)
- b. Vector Addition (向量加法)
- 3. A Single Neuron with NumPy
- 4. A Layer of Neurons with NumPy
- 5. A Batch of Data
- 6. Matrix Product
- 7. Transposition for the Matrix Product
- 8. A Layer of Neurons & Batch of Data w/ NumPy
引言
本教程专为那些对神经网络已有基础了解、但尚未动手实践过的读者而设计。尽管网上充斥着各种教程,但很多内容要么过于简略,要么直接进入高级主题,让初学者难以跟上。本指南将带领你从零开始,用 Python 构建一个简单的神经网络模型,逐步拆解每一步,帮助你真正理解神经网络的工作原理,为今后的深入学习打下坚实基础。
1. Tensors, Arrays and Vectors:
张量、数组和向量
简单的列表:
l = [1,5,6,2]
列表中的列表:
lol = [[1,5,6,2],[3,2,1,3]]
列表中的列表中的列表:
lolol = [[[1,5,6,2],[3,2,1,3]],[[5,2,1,2],[6,4,8,4]],[[2,8,5,3],[1,1,9,4]]]
另一种列表中的列表:
another_list_of_lists = [[4,2,3],[5,1]]
列表,矩阵,数组(这个数组的“形状”是3x2,或者更正式地描述为形状为(3, 2),因为它有3行和2列。):
list_matrix_array = [[4,2],[5,1],[8,2]]
对于三维数组,如下面的lolol,我们将有第三层括号:
lolol = [[[1,5,6,2],[3,2,1,3]],[[5,2,1,2],[6,4,8,4]],[[2,8,5,3],[1,1,9,4]]]
该数组的第一层包含 3 个矩阵:
[[1,5,6,2],[3,2,1,3]][[5,2,1,2],[6,4,8,4]][[2,8,5,3],[1,1,9,4]]
Shape: (3, 2, 4)
Type: 3D Array, List, Matrix
当然,如果直接复制粘贴再使用type()函数得到的肯定是<class 'list'>,我这里只是描述了数据可能的各种形式,重点在3D
2. Dot Product and Vector Addition
点积与向量加法
a. Dot Product (点积)

a = [1,2,3]
b = [2,3,4]dot_product = a[0]*b[0] + a[1]*b[1] + a[2]*b[2]print("dot_product:", dot_product)
dot_product: 20
代码的可视化:https://nnfs.io/xpo/
现在,如果我们将 a a a 称为“输入”(inputs),将 b b b 称为“权重”(weights)呢?突然间,这个点积看起来就像一种简洁的方式来执行我们需要的操作,而且已经在纯Python中执行过了。我们需要将相同索引值的权重和输入相乘,并将结果值加在一起。点积恰好执行这种类型的操作;因此,在这里使用它非常有意义。回到神经网络代码中,让我们利用这个点积。纯Python不包含执行此类操作的方法或函数,因此我们将使用NumPy包,它能够执行这个操作,以及未来我们将使用的许多更多操作。
b. Vector Addition (向量加法)
我们不久的将来也需要执行一个向量加法操作。幸运的是,NumPy允许我们以一种自然的方式进行这个操作——使用加号和包含数据向量的变量。两个向量的加法是逐元素执行的操作,这意味着两个向量必须具有相同的大小,结果也将成为这种大小的向量。结果是一个向量,作为连续向量元素的和计算得出:
a ⃗ + b ⃗ = [ a 1 + b 1 , a 2 + b 2 , … , a n + b n ] \vec{a} + \vec{b} = [a_1 + b_1, a_2 + b_2, \ldots, a_n + b_n] a+b=[a1+b1,a2+b2,…,an+bn]
3. A Single Neuron with NumPy
使用 NumPy 的单个神经元
import numpy as npinputs = [1.0, 2.0, 3.0, 2.5]
weights = [0.2, 0.8, -0.5, 1.0]
bias = 2.0outputs = np.dot(weights, inputs) + biasprint("outputs:", outputs)
outputs: 4.8

代码的可视化:https://nnfs.io/blq
4. A Layer of Neurons with NumPy
使用 NumPy 创建神经元层
import numpy as npinputs = [1.0, 2.0, 3.0, 2.5]
weights = [[0.2, 0.8, -0.5, 1],[0.5, -0.91, 0.26, -0.5],[-0.26, -0.27, 0.17, 0.87]]
biases = [2.0, 3.0, 0.5]layer_outputs = np.dot(weights, inputs) + biases # (3X4).(1X4)print("layer_outputs:", layer_outputs)
print("Type of layer_outputs:", type(layer_outputs))
layer_outputs: [4.8 1.21 2.385] # array([4.8 1.21 2.385])
Type of layer_outputs: <class 'numpy.ndarray'>

代码的可视化:https://nnfs.io/cyx
5. A Batch of Data
一批数据
为了训练,神经网络往往会成批接收数据。到目前为止,示例输入数据只是各种特征的一个样本(或观测值),称为特征集:
inputs = [1, 2, 3, 2.5]
在这里,[1, 2, 3, 2.5] 数据对我们想要的输出具有一定的意义和描述性。想象一下,每个数字都是同时来自不同传感器的值。每个值都是一个特征观测数据,它们共同构成一个特征集实例,也称为观测值,或最常见的样本。
通常,神经网络期望一次处理多个样本,原因有两个。一个原因是在并行处理中分批训练速度更快,另一个原因是分批可以在训练过程中帮助泛化。如果你一次只对一个样本进行拟合(执行训练过程的一个步骤),你很可能会一直只针对那个单一样本进行拟合,而不是逐渐对权重和偏差进行普遍的微调,以适应整个数据集。分批训练或拟合使你有更高的机会对权重和偏差进行更有意义的改变。关于分批拟合而不是一次一个样本的概念,以下动画可以帮助理解:https://nnfs.io/vyu
一批数据的示例如下:
Input data:batch = [[1,5,6,2],[3,2,1,3],[5,2,1,2],[6,4,8,4],[2,8,5,3],[1,1,9,4],[6,6,0,4],[8,7,6,4]]
Shape: (8, 4)
Type: 2D Array, Matrix
回想一下,在 Python 中,以及在我们的案例中,列表是非常有用的容器,用于存放单个样本以及组成一批观测数据的多个样本。这样一个观测批次的例子,每个样本都有自己的数据,看起来像这样:
inputs = [[1, 2, 3, 2.5], [2, 5, -1, 2], [-1.5, 2.7, 3.3, -0.8]]
这个列表中的列表可以转换成一个数组,因为它们是同构的。注意,这个更大列表中的每个“列表”都是一个样本,代表一组特征。[1, 2, 3, 2.5], [2, 5, -1, 2], [-1.5, 2.7, 3.3, -0.8] 都是样本,也被称为特征集实例或观测值。
现在我们有了一个输入矩阵和一个权重矩阵,我们需要以某种方式对它们进行点积运算,但是如何进行,结果又会是什么呢?类似于我们之前对矩阵和向量进行的点积运算,我们将矩阵视为向量列表,结果得到了一个点积列表。在这个例子中,我们需要将两个矩阵都管理为向量列表,并对所有的组合进行点积运算,结果是一个输出列表的列表,或者说是一个矩阵;这个操作称为矩阵乘积。
6. Matrix Product
矩阵乘积
矩阵乘积是一种操作,在这个操作中我们有两个矩阵,并且我们正在执行第一个矩阵的行与第二个矩阵的列的所有组合的点积,结果是这些原子点积组成的一个矩阵:

代码的可视化:https://nnfs.io/jei/
要执行矩阵乘积,左侧矩阵的第二维度的大小必须与右侧矩阵的第一维度的大小相匹配。例如,如果左侧矩阵的形状为 ( 5 , 4 ) (5, 4) (5,4),那么右侧矩阵的第一个形状值必须匹配这个 4(如 ( 4 , 7 ) (4, 7) (4,7))。结果数组的形状始终是左侧数组的第一维度和右侧数组的第二维度,即 ( 5 , 7 ) (5, 7) (5,7)。在上述示例中,左侧矩阵的形状为 ( 5 , 4 ) (5, 4) (5,4),右上方矩阵的形状为 ( 4 , 5 ) (4, 5) (4,5)。左侧数组的第二维度和第二个数组的第一维度都是 4,它们匹配,结果数组的形状为 ( 5 , 5 ) (5, 5) (5,5)。
进一步阐述,我们也可以展示我们可以对向量执行矩阵乘积。在数学中,我们可以有所谓的列向量和行向量,这些将很快更好地解释。它们是向量,但表示为矩阵,其中一个维度的大小为 1:

a a a 是一个行向量。它看起来与我们之前描述的向量 a ⃗ \vec{a} a 非常相似,后者是与向量积一起描述的。行向量和向量的符号之间的区别在于数值之间有逗号,而行向量上的符号 a a a 上没有箭头。它被称为行向量,因为它是矩阵的一行。另一方面, b b b 被称为列向量,因为它是矩阵的一列。由于行向量和列向量从技术上讲是矩阵,我们不再用向量箭头来表示它们。
当我们对它们进行矩阵乘积时,结果也变成了一个矩阵,就像前面的例子一样,但只包含一个值,这个值与我们之前讨论过的点积示例中的值相同:

代码的可视化:https://nnfs.io/bkw/
换句话说,行向量和列向量是其中一个维度大小为 1 的矩阵;并且,我们对它们执行矩阵乘积,而不是点积,这会得到一个只包含单个值的矩阵。在这个例子中,我们进行了形状为 ( 1 , 3 ) (1, 3) (1,3) 和 ( 3 , 1 ) (3, 1) (3,1) 的矩阵的矩阵乘法,然后得到的数组形状为 ( 1 , 1 ) (1, 1) (1,1) 或大小为 1 × 1 1 \times 1 1×1。
7. Transposition for the Matrix Product
矩阵积的移位
我们是如何突然从两个向量转变到行向量和列向量的?我们使用了点积和矩阵乘积之间的关系,表明两个向量的点积等于一个行向量和一个列向量的矩阵乘积(字母上方的箭头表示它们是向量):

我们还临时使用了一些简化,没有显示列向量 b b b 实际上是向量 b b b 的转置。正确的方程,将向量 a a a 和 b b b 的点积写作矩阵乘积的形式,应该看起来像:

这里我们介绍了另一种新操作——转置。转置简单地修改矩阵,使其行变成列,列变成行:

代码的可视化:https://nnfs.io/qut,https://nnfs.io/pnq
行向量是一个矩阵,其第一维的大小(行数)等于 1,第二维的大小(列数)等于 n n n —— 向量的大小。换句话说,它是一个 1 × n 1 \times n 1×n 的数组或形状为 ( 1 , n ) (1, n) (1,n) 的数组:

如果使用 NumPy 并使用 3 个值,我们可以将其定义为:
np.array([[1, 2, 3]])
请注意这里使用了双括号。为了将一个列表转换为包含单行的矩阵(执行将向量转换为行向量的等效操作),我们可以将其放入一个列表中,并创建 numpy 数组:
import numpy as npa = [1, 2, 3]
b = np.array([a])print("B:", b)
print("Type of B:", type(b))
B: [[1 2 3]] # array([[1, 2, 3]])
Type of B: <class 'numpy.ndarray'>
再次注意,在这种情况下,在转换为数组之前,我们将 a a a 放在括号内封装起来。或者我们可以将其转换为一维数组,并利用 NumPy 的功能之一扩展维度:
a = [1, 2, 3]
b = np.expand_dims(np.array(a), axis=0)print("B:", b)
print("Type of B:", type(b))
B: [[1 2 3]] # array([[1, 2, 3]])
Type of B: <class 'numpy.ndarray'>
其中 np.expand_dims() 在轴的索引处添加一个新的维度。
列向量是一个矩阵,其中第二维的大小等于 1,换句话说,它是一个形状为 ( n , 1 ) (n, 1) (n,1) 的数组:

使用 NumPy 创建列向量的方式与创建行向量相同,但需要额外进行转置——转置会将行变成列,列变成行:

为了将向量 b b b 转换为行向量 b b b,我们将使用与将向量 a a a 转换为行向量 a a a 相同的方法,然后我们可以对其进行转置,使其成为列向量 b b b:

使用 NumPy 代码:
import numpy as npa = [1, 2, 3]
b = [2, 3, 4]a = np.array([a])
b_T = np.array([b]).Tc = np.dot(a, b_T)print("a:", a)
print("Transpose of b:", b_T)
print("c:", c)
a: [[1 2 3]]
Transpose of b: [[2][3][4]]
c: [[20]] # array([[20]])
我们已经达到了与两个向量的点积相同的结果,但是这次操作是在矩阵上进行的,并返回了一个矩阵——这正是我们所期望和想要的。值得一提的是,NumPy 没有一个专门用于执行矩阵乘积的方法——点积和矩阵乘积都是在一个方法中实现的:np.dot()。
正如我们所见,要在两个向量上执行矩阵乘积,我们将其中一个按原样转换成行向量,而将另一个通过转置转换成列向量。这使我们能够执行一个返回包含单个值的矩阵的矩阵乘积。我们还在两个示例数组上执行了矩阵乘积,以了解矩阵乘积的工作原理——它创建了一个由所有行向量和列向量组合的点积构成的矩阵。
8. A Layer of Neurons & Batch of Data w/ NumPy
使用 NumPy 生成一层神经元和一批数据
让我们回到我们的输入和权重——在讨论它们时,我们提到需要对由输入和权重矩阵组成的所有向量进行点积运算。正如我们刚刚学到的,这正是矩阵乘积执行的操作。我们只需要对其第二个参数进行转置,即在我们的情况下是权重矩阵,以将其当前包含的行向量转换为列向量。
最初,我们能够在输入和权重上执行点积,而不需要转置,因为权重是一个矩阵,但输入只是一个向量。在这种情况下,点积的结果是一个向量,这个向量是在矩阵的每一行和这一个单独的向量上执行的原子点积。当输入变成一批输入(一个矩阵)时,我们需要执行矩阵乘积。它取来自左矩阵的所有行和右矩阵的所有列的组合,对它们进行点积运算,并将结果放置在一个输出数组中。两个数组具有相同的形状,但为了执行矩阵乘积,第一个矩阵的索引1的形状值和第二个矩阵的索引0的形状值必须匹配——现在它们不匹配。

如果我们对第二个数组进行转置,其形状的值就会交换位置。

代码的可视化:https://nnfs.io/crq
如果我们从输入和权重的角度来看这个问题,我们需要对每个输入和每组权重的所有组合执行点积运算。点积从第一个数组中取一行,从第二个数组中取一列,但目前两个数组中的数据都是按行对齐的。转置第二个数组使数据按列对齐。输入和转置权重的矩阵乘积将产生一个包含我们需要计算的所有原子点积的矩阵。结果矩阵包含了在每个输入样本上执行操作后所有神经元的输出:

代码的可视化:https://nnfs.io/gjw
我们提到,np.dot()的第二个参数将是我们的转置权重,所以第一个参数是输入,但之前权重是第一个参数。我们在这里改变了这一点。之前,我们使用单个数据样本(一个向量)来模拟神经元输出,但现在我们在对一批数据模拟层行为时向前迈进了一步。我们可以保留当前的参数顺序,但是,正如我们很快会了解到的,拥有一个由每个样本的层输出组成的结果列表比一个由神经元及其输出按样本组成的列表更有用。我们希望结果数组与样本相关,而不是与神经元相关,因为我们将把这些样本进一步传递给网络,而下一层将期待一批输入。
我们现在可以使用 NumPy 编码这个解决方案。我们可以对一个纯 Python 列表的列表执行 np.dot(),因为 NumPy 会在内部将它们转换为矩阵。不过,我们自己正在转换权重,以便首先执行转置操作(在代码中为 T),因为纯 Python 列表的列表不支持这种操作。至于偏置,我们不需要将其制作成 NumPy 数组,原因相同——NumPy 将在内部完成这个操作。
偏置是一个列表,所以它们作为 NumPy 数组是一维数组。这个偏置向量加到矩阵上(在这种情况下是点积的矩阵)的方式与我们之前描述的矩阵和向量的点积类似;偏置向量将被添加到矩阵的每个行向量上。由于矩阵乘积结果的每一列是一个神经元的输出,并且向量将被添加到每个行向量上,第一个偏置将被添加到这些向量的每个第一个元素上,第二个添加到第二个,依此类推。这正是我们需要的——每个神经元的偏置需要被添加到此神经元在所有输入向量(样本)上执行的所有结果上。

代码的可视化:https://nnfs.io/qty
现在,我们可以将所学知识转化为代码:
import numpy as npinputs = [[1.0, 2.0, 3.0, 2.5],[2.0, 5.0, -1.0, 2.0],[-1.5, 2.7, 3.3, -0.8]]weights = [[0.2, 0.8, -0.5, 1.0],[0.5, -0.91, 0.26, -0.5],[-0.26, -0.27, 0.17, 0.87]]biases = [2.0, 3.0, 0.5]layer_outputs = np.dot(inputs, np.array(weights).T) + biasesprint("layer_outputs:", layer_outputs)
print("Type of layer_outputs:", type(layer_outputs))
layer_outputs: [[ 4.8 1.21 2.385] # array([[ 4.8 1.21 2.385],[ 8.9 -1.81 0.2 ] # [ 8.9 -1.81 0.2 ],[ 1.41 1.051 0.026]] # [ 1.41 1.051 0.026]])
Type of layer_outputs: <class 'numpy.ndarray'>
代码的可视化:https://nnfs.io/ch2
如您所见,我们的神经网络接收一组样本(输入)并输出一组预测。如果您使用过任何深度学习库,这就是为什么您会传入一系列输入(即使只是一个特征集)并返回一系列预测的原因,即使只有一次预测。
相关文章:

用 Python 从零开始创建神经网络(二)
用 Python 从零开始创建神经网络(二) 引言1. Tensors, Arrays and Vectors:2. Dot Product and Vector Additiona. Dot Product (点积)b. Vector Addition (向量加法) 3. A Single Neuron with …...

嘉吉连续第七年亮相进博会
以“新质绿动,共赢未来”为主题,嘉吉连续第七年亮相进博会舞台。嘉吉带来了超过120款产品与解决方案,展示嘉吉在农业、食品、金融和工业等领域以客户为中心的创新成果。这些产品融合了嘉吉在相关领域的前瞻性思考,以及对本土市场的…...

设计模式之单列模式(7种单例模式案例,Effective Java 作者推荐枚举单例模式)
前言 在设计模式中按照不同的处理方式共包含三大类;创建型模式、结构型模式和行为模式,其中创建型模式目前已经介绍了其中的四个;工厂方法模式、抽象工厂模式、生成器模式和原型模式,除此之外还有最后一个单例模式。 单列模式介绍…...

多个服务器共享同一个Redis Cluster集群,并且可以使用Redisson分布式锁
Redisson 是一个高级的 Redis 客户端,它支持多种分布式 Java 对象和服务。其中之一就是分布式锁(RLock),它可以跨多个应用实例在多个服务器上使用同一个 Redis 集群,为这些实例提供锁服务。 当你在不同服务器上运行的…...

100种算法【Python版】第59篇——滤波算法之扩展卡尔曼滤波
本文目录 1 算法步骤2 算法示例2.1 示例描述2.2 python代码3 算法应用:机器人位姿估计扩展卡尔曼滤波(EKF)是一种处理非线性系统的状态估计算法。它通过线性化非线性系统来实现类似于线性卡尔曼滤波的效果。 1 算法步骤 (1)初始化 初始状态: x ^ 0 ∣ 0 \hat{x}_{0|0}...

制造业数字化转型的强大赋能平台:盘古信息IMS OS工软技术底座
在制造业数字化转型的浪潮中,技术底座的选择与实施至关重要。它不仅决定了企业数字化转型的深度与广度,还影响着企业的生产效率、成本控制和市场竞争力。盘古信息IMS OS作为一款强大的工软技术底座,凭借其高度模块化、可配置的设计理念&#…...

域名+服务器+Nginx+宝塔使用SSL证书配置HTTPS
前言 在我的前面文章里,有写过一篇文章 linux服务器宝塔从头部署别人可访问的网站 在这篇文章,有教学怎么使用宝塔和买的服务器的公网IP,以及教怎么打包vue和springboot去部署不用域名的网站让别人访问 那么,这篇文章将在这个…...
UnityAssetsBundle字体优化解决方案
Unity开发某个项目,打包后的apk包体已经高达1.25G了,这是非常离谱的。为了不影响用户体验,需要将apk包体缩小。因为项目本身不包含很多模型以及其他大型资源,排除法将AB包删除,发现app本身就100多M。 由此可以锁定是AB…...
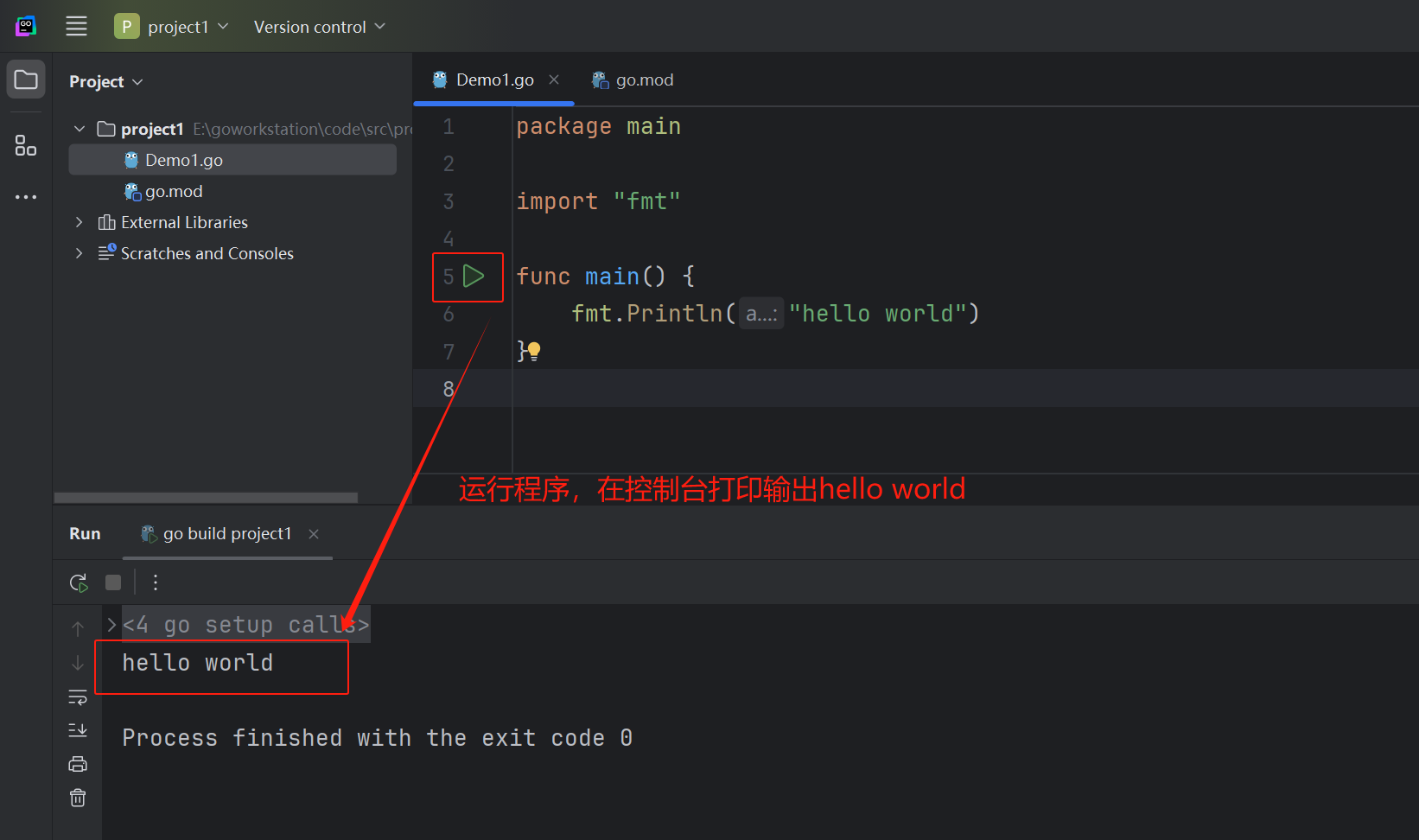
Go的环境搭建以及GoLand安装教程
目录 一、开发环境Golang安装 二、配置环境变量 三、GoLand安装 四、Go 语言的 Hello World 一、开发环境Golang安装 官方网址: The Go Programming Language 1. 首先进入官网,点击Download,选择版本并进行下载: 2. …...

git clone,用https还是ssh
前言 在使用Git去克隆项目时,会遇到https和ssh等形式,这两种又有何种区别呢,本文将重点讨论在具体使用中的问题。 注:第一次使用Git 时,需要先设置全局用户名和邮箱,否则后续使用命令时会报错,也是提醒先添…...

量化交易系统开发-实时行情自动化交易-Okex行情交易数据
19年创业做过一年的量化交易但没有成功,作为交易系统的开发人员积累了一些经验,最近想重新研究交易系统,一边整理一边写出来一些思考供大家参考,也希望跟做量化的朋友有更多的交流和合作。 接下来聊聊基于Okex交易所API获取行情数…...

【重装系统后重新配置2】pycharm 终端无法激活conda环境
pycharm 终端无法激活 conda 环境,但是 Windows本地终端是可以激活的 原因是pycharm 默认的终端是 Windows PowerShell 解决方法有两个: 一、在设置里,修改为cmd 二、下面直接选择...

【LeetCode每日一题】——802.找到最终的安全状态
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时空频度】九【代码实现】十【提交结果】 一【题目类别】 图 二【题目难度】 中等 三【题目编号】 802.找到最终的安全状态 四【题目描述】 有一个有…...

kafka安装部署--详细教程
2.1 安装部署 每次进入 linux 都会自动进入 base 环境,如何关闭 base conda deactivate 手动关闭 conda config --set auto_activate_base false 关闭自动进入 2.1.1 集群规划 bigdata01 bigdata02 bigdata03 zk zk zk kafka kafka kafka 2.1.2 集群部…...

CMD 查询python 出现 No pyvenv.cfg file 很奇怪 2024/11/9
CMD 查询python 出现 No pyvenv.cfg file 很奇怪 查询得到我有很多个...........版本 删除这个变量就不会 因为 没有安装软件 跳转到 Windows 商店 再把主要使用的python路径置顶 现在运行cmd查询 对比之前的图片 可以发现 这一条商店的没有了! 完整测试效果,问题解决了!...

learnopencv系列二:U2-Net/IS-Net图像分割(背景减除)算法、使用背景减除实现视频转ppt应用
文章目录 一、视频转幻灯片应用1.1 什么是背景减除?1.1.1 背景减除简介1.1.2 bgslibrary 1.2 OpenCV背景减除技术1.3 差异哈希1.3.1 图像哈希技术1.3.2 dHash算法1.3.3 图像哈希的速度和准确性测试 1.4 视频转幻灯片应用的工作流程1.5 项目代码1.5.1 环境准备1.5.2 …...
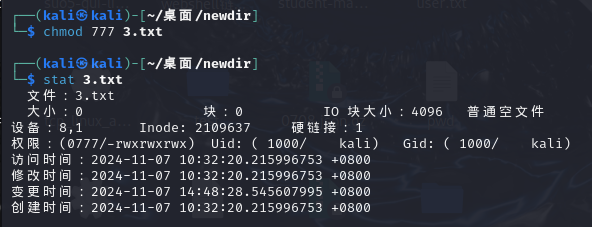
linux命令详解,文件系统权限相关
文件系统权限相关 linux系统中一切都是文件 查看权限 Is -la /etc/passwd更改文件所有者 chown root file修改文件权限 sudo chmod urwx,grw,o-r file sudo chmod ux,gtw,o-r file chmod 400 <file>一、Linux系统中一切都是文件 在linux系统中,几乎所有的…...
)
2024-11-5 学习人工智能的Day22 openCV(4)
face_recognition 介绍 face_recognition 是一个非常流行的 Python 库,专门用于人脸识别任务。它基于 dlib 库和 HOG(Histogram of Oriented Gradients)特征以及深度学习模型,提供了简单易用的接口来进行人脸检测、面部特征点定位…...

JavaScript 网页设计详解教程
JavaScript 网页设计详解教程 引言 JavaScript 是一种广泛使用的编程语言,主要用于网页开发。它使得网页具有动态交互性,能够响应用户的操作。随着前端开发的不断发展,JavaScript 已成为现代网页设计中不可或缺的一部分。本文将详细介绍 Ja…...
技术复杂性导致估算不准确?5大对策
技术复杂性引发的估算不准确可能导致成本超出预算,不当的资源分配则可能造成人力浪费或关键任务缺乏必要支持,进而影响客户满意度和市场竞争力,增加项目失败的风险。而有效避免因技术复杂性导致的估算不准确问题,可以显著提升项目…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
