【王木头】最大似然估计、最大后验估计
目录
一、最大似然估计(MLE)
二、最大后验估计(MAP)
三、MLE 和 MAP 的本质区别
四、当先验是均匀分布时,MLE 和 MAP 等价
五、总结
本文理论参考王木头的视频:
贝叶斯解释“L1和L2正则化”,本质上是最大后验估计。如何深入理解贝叶斯公式?_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1fR4y177jP/?spm_id_from=333.999.0.0&vd_source=ecbdfcacb078d0e3626e61248866cdc7
https://www.bilibili.com/video/BV1fR4y177jP/?spm_id_from=333.999.0.0&vd_source=ecbdfcacb078d0e3626e61248866cdc7
一、最大似然估计(MLE)
先读文章,里面有最大似然估计的例子和分析。
【王木头·从感知机到神经网络】-CSDN博客![]() https://blog.csdn.net/m0_56997192/article/details/142876334?spm=1001.2014.3001.5502在最大似然估计中,有两个不严谨的地方:
https://blog.csdn.net/m0_56997192/article/details/142876334?spm=1001.2014.3001.5502在最大似然估计中,有两个不严谨的地方:
1、在上文抛硬币的例子中,已有结果,求某先验
的概率
,在计算时我们把
假设为了
,实际上
,但我们最大似然确认为他们相等了,我们想要求的是已确定某个结果,哪个先验的情况下概率最大;但我们实际求的是某个先验时发生事件的概率的最大值,
即目的是求 ,
但实际求的是 ,
被称为似然值或似然函数,记为
,
似然函数为:
最大似然估计为:
想到这,我似乎想到了”似然“两个字的起名原因,我们要解决问题,就要求出,但
无法直接求出,所以我们选用了一个与
“ 相似 ” 的
,所以
叫做似然值,“ 相似 ”的对象是
。
2、另一个王木头提到的是:
最大似然估计为:中的
是永远无法确定的,但我们把概率最大的
跳出来人为规定他就是系统本来就有的属性,这个点我不理解,不过我感觉没什么用。
二、最大后验估计(MAP)
在最大似然估计中,有一个不严谨的地方是让 ,实际上他们是不相等的,我们要求的是
但最大似然估计中求的是最大的
,最大后验估计解决了这个不严谨的问题。即由贝叶斯公式:
将不能计算的 转化为
其中:
是似然函数;
是先验分布;
- p
是边际似然(可以视为常数,与优化无关)。
因此,MAP估计的目标可以等价于最大化 :
在对数形式下,MAP可以写成:
最大后验估计MAP的特点:
- 考虑先验信息:MAP结合了观测数据和参数的先验知识。先验信息通过
反映了我们对参数可能取值的先验信念。
- 贝叶斯统计:MAP是贝叶斯估计方法的一种,将参数视为随机变量,通过观测数据更新我们对参数的信念。
- 适用于小样本数据:MAP可以在样本较少的情况下引入先验信息,提供稳定的估计。
三、MLE 和 MAP 的本质区别
从本质上来说,MLE 和 MAP 的主要区别在于:
-
先验的使用:
- MLE 只基于数据的似然函数进行参数估计,不考虑任何先验信息。
- MAP 则通过先验分布
将先验信息纳入估计中,因此 MAP 是贝叶斯估计的一种。
-
适用场景的差异:
- MLE 在大样本情况下表现很好,因为在大样本极限下,观测数据对估计的影响远大于先验。
- MAP 更适合小样本或需要引入先验信息的情况,因为先验可以在样本较少时提供稳定性,避免估计过于依赖有限的观测数据。
-
计算的差异:
- MLE 的目标是最大化似然函数
。
- MAP 的目标是最大化后验概率
,相当于最大化
。
- MLE 的目标是最大化似然函数
四、当先验是均匀分布时,MLE 和 MAP 等价
值得注意的是,如果先验分布 是均匀的(即假设所有参数值的先验概率相同),则
是一个常数,这样 MAP 的目标函数就变为:
常数
在这种情况下,最大化 ( 常数) 等价于最大化
,因此 MAP 和 MLE 会得到相同的结果。
这意味着,在没有先验或先验均匀的情况下,MAP 退化为 MLE。因此,MAP 可以被视为 MLE 的一种推广,它允许我们在估计中融入先验信息。
五、总结
本质区别在于:
- 最大似然估计MLE 只依赖数据的似然,不使用先验,是一种频率派的估计方法。
- 最大后验估计MAP 同时考虑数据的似然和参数的先验信息,是一种贝叶斯派的估计方法。
总结公式:
- 最大似然估计MLE:
- 最大后验估计MAP:
在有先验信息的情况下,MAP 能够更好地利用先验信息对估计进行约束,而 MLE 则完全依赖观测数据。
相关文章:
【王木头】最大似然估计、最大后验估计
目录 一、最大似然估计(MLE) 二、最大后验估计(MAP) 三、MLE 和 MAP 的本质区别 四、当先验是均匀分布时,MLE 和 MAP 等价 五、总结 本文理论参考王木头的视频: 贝叶斯解释“L1和L2正则化”ÿ…...

智谱AI视频生成模型CogVideoX v1.5开源 支持5/10秒视频生成
今日,智谱技术团队发布了其最新的视频生成模型 CogVideoX v1.5,并将其开源。这一版本是自8月以来,智谱技术团队推出的 CogVideoX 系列中的又一重要进展。 据了解,此次更新大幅提升了视频生成能力,包括支持5秒和10秒的视…...

算法(第一周)
一周周五,总结一下本周的算法学习,从本周开始重新学习许久未见的算法,当然不同于大一时使用的 C 语言以及做过的简单题,现在是每天一题 C 和 JavaScript(还在学,目前只写了一题) 题单是代码随想…...

Linux服务器进程的控制与进程之间的关系
在 Linux 服务器中,进程控制和进程之间的关系是系统管理的一个重要方面。理解进程的生命周期、控制以及它们之间的父子关系对于系统管理员来说至关重要。以下是关于进程控制、进程之间的关系以及如何管理进程的详细介绍: 1. 进程的概念 进程࿰…...

机器学习Housing数据集
import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.datasets import fetch_openml 设置Seaborn的美观风格 sns.set(style“whitegrid”) Step 1: 下载 Housing 数据集,并读入计算机 def load_housing_data(): housing …...

随着最新的补丁更新,Windows 再次变得容易受到攻击
SafeBreach专家Alon Leviev发布了一款名为 Windows Downdate的工具,可用于对Windows 10、Windows 11 和 Windows Server 版本进行降级攻击。 这种攻击允许利用已经修补的漏洞,因为操作系统再次容易受到旧错误的影响。 Windows Downdate 是一个开源Pyth…...

【Python】爬虫通过验证码
1、将验证码下载至本地 # 获取验证码界面html url http://www.example.com/a.html resp requests.get(url) soup BeautifulSoup(resp.content.decode(UTF-8), html.parser)#找到验证码图片标签,获取其地址 src soup.select_one(div.captcha-row img)[src]# 验证…...
dc-aichat(一款支持ChatGPT+智谱AI+讯飞星火+书生浦语大模型+Kimi.ai+MoonshotAI+豆包AI等大模型的AIGC源码)
dc-aichat 一款支持ChatGPT智谱AI讯飞星火书生浦语大模型Kimi.aiMoonshotAI豆包AI等大模型的AIGC源码。全网最易部署,响应速度最快的AIGC环境。PHP版调用各种模型接口进行问答和对话,采用Stream流模式通信,一边生成一边输出。前端采用EventS…...

检索增强生成
检索增强生成 检索增强生成简介 检索增强生成(RAG)旨在通过检索和整合外部知识来增强大语言模型生成文本的准确性和丰富性,其是一个集成了外部知识库、信息检索器、大语言模型等多个功能模块的系统。 RAG 利用信息检索、深度学习等多种技术…...

操作系统--进程
2.1.1 进程的概念、组成、特征 进程的概念 进程的组成 进程的特征 总结 2.1.2 进程的状态与转换,进程的组织 创建态、就绪态 运行态 阻塞态 终止态 进程状态的转换 进程的组织 链式方式 索引方式 2.1.3 进程控制 如何实现进程控制? 在下面的例子,将PCB2的是state设为1和和把…...

abap 可配置通用报表字段级日志监控
文章目录 1.功能需求描述1.1 功能1.2 效果展示2.数据库表解释2.1 表介绍3.数据库表及字段3.1.应用日志数据库抬头表:ZLOG_TAB_H3.2.应用日志数据库明细表:ZLOG_TAB_P3.3.应用日志维护字段配置表:ZLOG_TAB_F4.日志封装类5.代码6.调用方式代码7.调用案例程序demo1.功能需求描述 …...

OpenCV视觉分析之目标跟踪(11)计算两个图像之间的最佳变换矩阵函数findTransformECC的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 根据 ECC 标准 78找到两幅图像之间的几何变换(warp)。 该函数根据 ECC 标准 ([78]) 估计最优变换(warpMatri…...

PGMP-串串0203 项目集管理绩效域战略一致性
1.项目集管理绩效域 2.战略一致性 战略一致性包含内容商业论证BC项目集章程项目集路线图环境评估项目集风险管理策略 前期formulation sub-phaseplanning sub-phase组织的战略计划项目集风险管理策略项目集管理计划商业论证BC项目集章程项目集路线图环境评估...

HiveMetastore 的架构简析
HiveMetastore 的架构简析 Hive Metastore 是 Hive 元数据管理的服务。可以把元数据存储在数据库中。对外通过 api 访问。 hive_metastore.thrift 对外提供的 Thrift 接口定义在文件 standalone-metastore/src/main/thrift/hive_metastore.thrift 中。 内容包括用到的结构体…...

【WRF模拟】全过程总结:WPS预处理及WRF运行
【WRF模拟】全过程总结:WPS预处理及WRF运行 1 数据准备1.1 嵌套域设置(Customize domain)-基于QGis中gis4wrf插件1.2 静态地理数据1.2.1 叶面积指数LAI和植被覆盖度Fpar(月尺度)1.2.2 地面反照率(月尺度)1.2.3 土地利用类型+不透水面积1.2.4 数据处理:geotiff→tiff(W…...
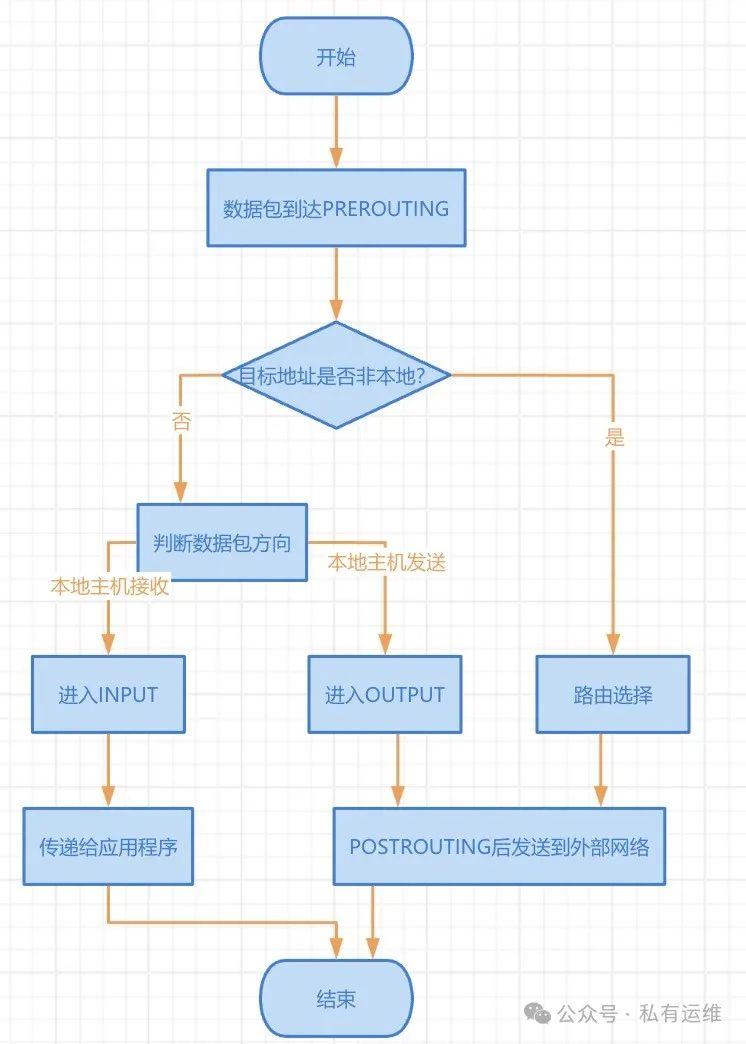
linux基础理解和使用 iptables 防火墙
本文档旨在编写一份详尽的 iptables基础 使用指南,涵盖其核心概念、使用方法以及高级技巧。将结合图表和示例,更好地理解和应用 iptables。 1. 什么是 iptables? iptables 是 Linux 系统自带的包过滤防火墙,它与内核空间的 netf…...
)
【系统架构设计师】2024年下半年真题论文: 论软件维护及其应用(包括参考素材)
更多内容请见: 备考系统架构设计师-专栏介绍和目录 文章目录 真题题目(2024年下半年 试题2)论文素材参考软件维护的类型软件维护的方法软件维护应用案例分析软件维护面临的挑战与应对策略真题题目(2024年下半年 试题2) 请围绕 “论软件维护及其应用” 论题,依次从以下三…...

【数学二】线性代数-矩阵-初等变换、初等矩阵
考试要求 1、理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质. 2、掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质. 3、理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可…...
MinerU容器构建教程
一、介绍 MinerU作为一款智能数据提取工具,其核心功能之一是处理PDF文档和网页内容,将其中的文本、图像、表格、公式等信息提取出来,并转换为易于阅读和编辑的格式(如Markdown)。在这个过程中,MinerU需要利…...

BFS 解决拓扑排序
BFS 解决拓扑排序 1.课程表1.1. 题⽬链接:1.2 题⽬描述:1.3. 解法:1.4 代码 2. 课程表2.1题⽬链接:2.2 题⽬描述:2.3解法:2.4代码 3. ⽕星词典(hard)3.1题⽬链接:3.2 题⽬…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
