大数据机器学习算法与计算机视觉应用03:数据流
Data Stream
- Streaming Model
- Example Streaming Questions
- Heavy Hitters
- Algorithm 1: For Majority element
- Misra Gries Algorithm
- Applications
- Approximation of count
Streaming Model 数据流模型
数据流就是所有的数据先后到达,而不是同时存储在内存之中。在现实中,数据流或者本身占用空间很大,或者数量很多,保存所有的数据流数据是不可能的。
因此,在数据流相关问题中,我们一般比较关注空间复杂度,也就是节省内存的做法。
本节课提到的数据流模型简单地用数字流来代表数据流,也就是说数据流中地每一个元素都是一个数。
Example Streaming Questions 经典数据流问题
我们假设每个数据需要 b b b 位来存储,总共预计接收到 t t t 个数据
1.维护接收到的所有数据的总和需要的位数
答案是 O ( b + log t ) O(b + \log t) O(b+logt)。
为什么是这个答案呢?
一个数是 b b b 位, t t t 个数就是 b + log t b+\log t b+logt位。这个和十进制里面,十个一位数相加的结果一定是一个 1 + log 10 = 2 1 + \log 10 =2 1+log10=2位数来表达一样。这就是这里为什么是元素个数取对数。
2. 维护收到的所有数据的最大值需要的位数
很明显答案是 O ( b ) O(b) O(b)。
3.维护收到的所有数据的中位数需要的位数
这个问题似乎有点困难。因为中位数涉及到对于所有数据进行排序。但是也不是完全没办法,请参见下文算法。
Heavy Hitters 频繁项
给定项数 n n n 和权重 ϵ \epsilon ϵ ,请你找到数据流中所有出现次数大于 ϵ n \epsilon n ϵn 的项。这就是数据流中的频繁项问题。我们如何在使用内存尽可能小的情况下解决这个问题呢?
Algorithm 1: For Majority element 主元算法
如果一个数据流中有一个数据的出现频率超过了0.5,那么这个数据就被叫做主元。我们可以先看看如何确定主元的算法,以便我们推广到频繁项。
可行的一个算法如下:
在内存中声明一个数k和一个计数器c.
初始化时,让k为空,让c为0.
每当数据 a i a_i ai 到达时,循环执行如下操作:
如果 c = 0 c=0 c=0 ,那么 a i → k a_i \rarr k ai→k, 1 → c 1 \rarr c 1→c;
如果 c ≠ 0 c\neq 0 c=0 且 a i ≠ k a_i \neq k ai=k,那么 c − − c-- c−−;
如果 c ≠ 0 c\neq0 c=0 且 a i = k a_i = k ai=k ,那么 c + + c++ c++;
循环执行该操作,执行完毕时的数k就可能是主元。
写成代码的形式如下:
datatype a,k;int c=0;cin >> a;while(a){if(c==0){k=a;c=1;}else if (c>0 && a!=k){c--;}else {c++;}}
注意,这个算法得到的结果不一定是主元,但是这个数是最可能是主元的那一个。
下面我们证明:如果数据流有主元 a m a i n a_{main} amain,那么主元一定是 k k k 。
每次读入 a m a i n a_{main} amain时,要么 k ≠ a m a i n , c − − k \neq a_{main}, c-- k=amain,c−− ,要么 k = a m a i n , c + + k = a_{main}, c++ k=amain,c++ ;因为是主元,所以必定存在某个时刻使得 k = a m a i n k = a_{main} k=amain,且因为 c++ 的次数大于 c-- 的次数,因此读入所有数据之后一定满足 k = a m a i n k = a_{main} k=amain。
这个算法的主要思路是,由于我们寻找主元,而一个数据流中主元最多就一个,因此我们只需要记录那个可能出现次数过半的就可以了。如果有主元,那么这个数据
一定会被记录下来。但是我们不知道记录下来的是否一定是主元。即这是一个充分不必要条件:
有主元 ⇒ k 是主元 有主元 \rArr k是主元 有主元⇒k是主元
Misra Gries Algorithm MG算法
MG算法是上面算法的一个拓展,用于计算 ϵ \epsilon ϵ 频繁项。如果主元使用一个数来记录,那么最多可以有几个 ϵ \epsilon ϵ 频繁项开一个对应大小的数组就可以了。答案是 ⌈ ( 1 ϵ ) ⌉ − 1 \lceil(\frac{1}{\epsilon})\rceil -1 ⌈(ϵ1)⌉−1.为什么是这个数呢? ϵ \epsilon ϵ 带入一下 2 5 \frac{2}{5} 52 和 1 2 \frac{1}{2} 21 就知道了。
我们声明一个数组 T [ k ] T[k] T[k] 负责存储数据,数组 C [ k ] C[k] C[k]负责存储计数器,算法大同小异。其伪代码形式如下:
datatype a,T[k];int C[k]={0};while(cin >> a){if(C[j]==0){T[j]=a;C[j]=1;}else if (C[j]!=0 && a!=T[j]){all C[j]--;}else if(a==T[j]){C[j]++;}}
Heavy Hitters Guarantee
为什么MG算法可以保证找出所有的频繁项呢?证明方法也是和上面的算法一样。
我们在此证明:
0 ≤ c o u n t t ( e ) − e s t t ( e ) ≤ n k + 1 ≤ ϵ ⋅ n 0 \leq count_t(e) - est_t(e) \leq \frac{n}{k} +1 \leq \epsilon\cdot n 0≤countt(e)−estt(e)≤kn+1≤ϵ⋅n
其中 c o u n t t ( e ) count_t(e) countt(e)是某个元素 e e e实际出现的次数, e s t t ( e ) est_t(e) estt(e)是指该元素的计数器次数。
等式的左边不难证明,因为我们要在实际接收到一个相同元素之后才会把计数器+1,因此实际次数-计数器次数一定大于0
等式的右边是因为每次所有计数器-1的操作都至少需要k次单个计数器+1的操作,因此减少所有计数器的操作最多只有 n k + 1 \frac{n}{k+1} k+1n 次。
那么对于频繁项, c o u n t t ( e ) > ϵ ⋅ n count_t(e) > \epsilon \cdot n countt(e)>ϵ⋅n,而又有 c o u n t t ( e ) − e s t t ( e ) ≤ ϵ ⋅ n count_t(e) - est_t(e) \leq \epsilon\cdot n countt(e)−estt(e)≤ϵ⋅n,因此 e s t t ( e ) > 0 est_t(e) >0 estt(e)>0,也就是所有的频繁项一定会在列表之中。注意,所有的频繁项一定在列表之中不代表列表中的所有项都是频繁项。
Space Complexity 空间复杂度
MG算法的空间复杂度就是两个数组的空间复杂度:
O ( k ( log ∣ Σ ∣ + log n ) ) b i t s O(k(\log |\Sigma| +\log n))bits O(k(log∣Σ∣+logn))bits
两个数组的长度都是 k k k,数据数组每个元素需要 log ∣ Σ ∣ \log |\Sigma| log∣Σ∣位来存储(表示数据的范围),计数器数组每隔元素需要 log n \log n logn位来存储(表示从0到n)。
Applications
-
Internet router may want to figure out which IP connections are heavy hitters, e.g., the ones that use more than 0.01% of your bandwidth.(寻找网络中哪些IP地址是常被访问的)
-
Or the median of the file sizes being transferred.(文件大小的中位数)
相关文章:

大数据机器学习算法与计算机视觉应用03:数据流
Data Stream Streaming ModelExample Streaming QuestionsHeavy HittersAlgorithm 1: For Majority elementMisra Gries AlgorithmApplicationsApproximation of count Streaming Model 数据流模型 数据流就是所有的数据先后到达,而不是同时存储在内存之中。在现…...

【代码随想录day25】【C++复健】491.递增子序列;46.全排列;47.全排列 II;51. N皇后;37. 解数独
491.递增子序列 本题做的时候除了去重逻辑之外,其他的也勉强算是写出来了,不过还是有问题的,总结如下: 1 本题的关键:去重 与其说是不知道用什么去重,更应该说是完全没想到本题需要去重,说明…...

AI智能识物(微信小程序)
AI智能识物,是一款实用的小程序。可以拍照智能识物,可识别地标、车型、花卉、植物、动物、果蔬、货币、红酒、食材等等,AI智能技术识别准确度高。 更新说明: 此源码为1.2.0版本。 主要更新内容:新增security.imgSec…...

游戏引擎学习第三天
视频参考:https://www.bilibili.com/video/BV1XTmqYSEtm/ 之前的程序不能退出,下面写关闭窗体的操作 PostQuitMessage 是 Windows API 中的一个函数,用于向当前线程的消息队列发送一个退出消息。其作用是请求应用程序退出消息循环,通常用于处…...
帝国CMS7.5仿模板堂柒喜模板建站网 素材资源下载站源码
环境要求:phpmysql、支付伪静态 本套模板采用帝国cms7.5版UTF-8开发,一款非常不错的高端建站源码模板, 适用于中小型网络建站工作室源码模板下载站,支持自定义设置会员组。 源码下载:https://download.csdn.net/down…...
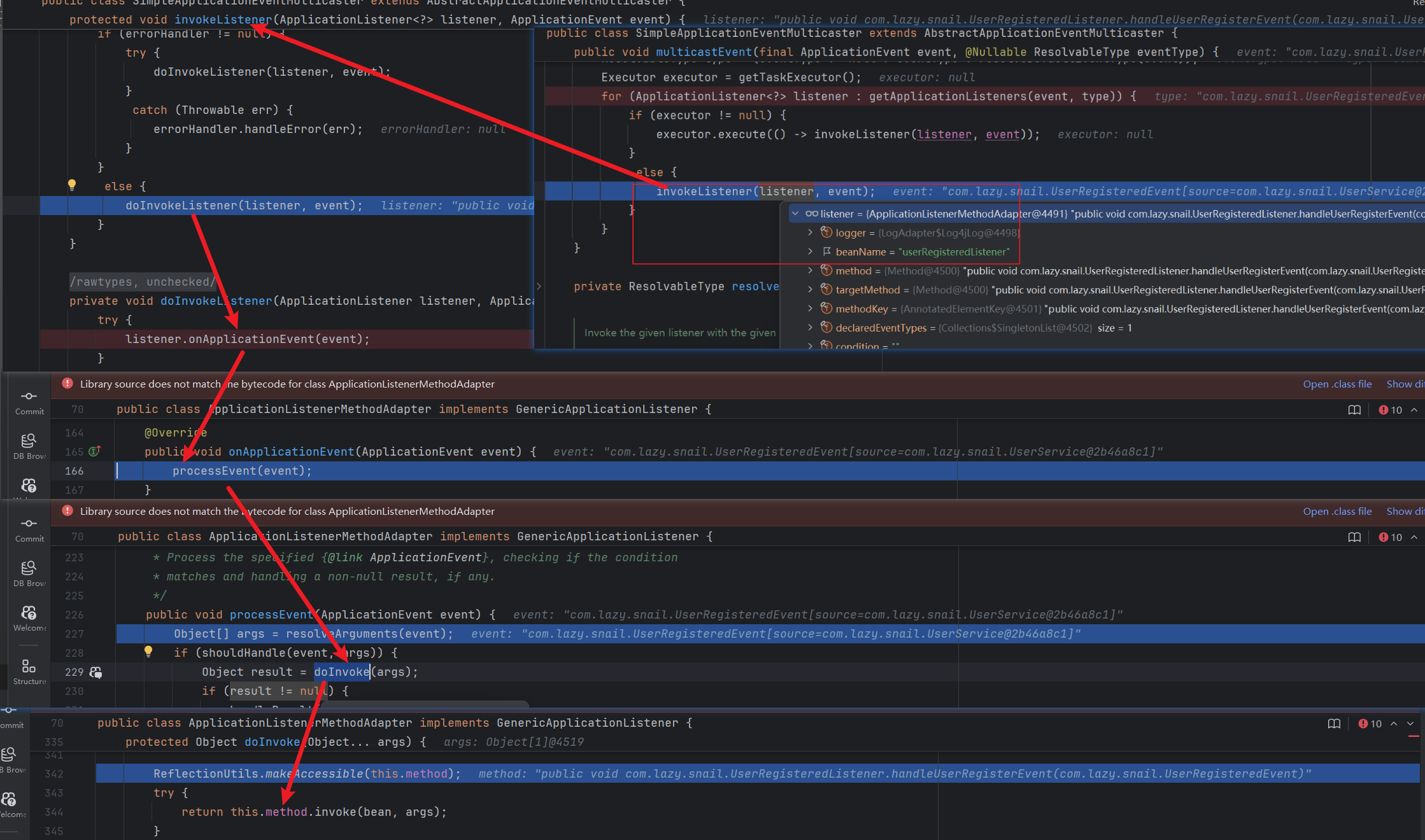
聊一聊Spring中的自定义监听器
前言 通过一个简单的自定义的监听器,从源码的角度分一下Spring中监听的整个过程,分析监听的作用。 一、自定义监听案例 1.1定义事件 package com.lazy.snail;import lombok.Getter; import org.springframework.context.ApplicationEvent;/*** Class…...
【王木头】最大似然估计、最大后验估计
目录 一、最大似然估计(MLE) 二、最大后验估计(MAP) 三、MLE 和 MAP 的本质区别 四、当先验是均匀分布时,MLE 和 MAP 等价 五、总结 本文理论参考王木头的视频: 贝叶斯解释“L1和L2正则化”ÿ…...

智谱AI视频生成模型CogVideoX v1.5开源 支持5/10秒视频生成
今日,智谱技术团队发布了其最新的视频生成模型 CogVideoX v1.5,并将其开源。这一版本是自8月以来,智谱技术团队推出的 CogVideoX 系列中的又一重要进展。 据了解,此次更新大幅提升了视频生成能力,包括支持5秒和10秒的视…...

算法(第一周)
一周周五,总结一下本周的算法学习,从本周开始重新学习许久未见的算法,当然不同于大一时使用的 C 语言以及做过的简单题,现在是每天一题 C 和 JavaScript(还在学,目前只写了一题) 题单是代码随想…...

Linux服务器进程的控制与进程之间的关系
在 Linux 服务器中,进程控制和进程之间的关系是系统管理的一个重要方面。理解进程的生命周期、控制以及它们之间的父子关系对于系统管理员来说至关重要。以下是关于进程控制、进程之间的关系以及如何管理进程的详细介绍: 1. 进程的概念 进程࿰…...

机器学习Housing数据集
import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.datasets import fetch_openml 设置Seaborn的美观风格 sns.set(style“whitegrid”) Step 1: 下载 Housing 数据集,并读入计算机 def load_housing_data(): housing …...

随着最新的补丁更新,Windows 再次变得容易受到攻击
SafeBreach专家Alon Leviev发布了一款名为 Windows Downdate的工具,可用于对Windows 10、Windows 11 和 Windows Server 版本进行降级攻击。 这种攻击允许利用已经修补的漏洞,因为操作系统再次容易受到旧错误的影响。 Windows Downdate 是一个开源Pyth…...

【Python】爬虫通过验证码
1、将验证码下载至本地 # 获取验证码界面html url http://www.example.com/a.html resp requests.get(url) soup BeautifulSoup(resp.content.decode(UTF-8), html.parser)#找到验证码图片标签,获取其地址 src soup.select_one(div.captcha-row img)[src]# 验证…...
dc-aichat(一款支持ChatGPT+智谱AI+讯飞星火+书生浦语大模型+Kimi.ai+MoonshotAI+豆包AI等大模型的AIGC源码)
dc-aichat 一款支持ChatGPT智谱AI讯飞星火书生浦语大模型Kimi.aiMoonshotAI豆包AI等大模型的AIGC源码。全网最易部署,响应速度最快的AIGC环境。PHP版调用各种模型接口进行问答和对话,采用Stream流模式通信,一边生成一边输出。前端采用EventS…...

检索增强生成
检索增强生成 检索增强生成简介 检索增强生成(RAG)旨在通过检索和整合外部知识来增强大语言模型生成文本的准确性和丰富性,其是一个集成了外部知识库、信息检索器、大语言模型等多个功能模块的系统。 RAG 利用信息检索、深度学习等多种技术…...

操作系统--进程
2.1.1 进程的概念、组成、特征 进程的概念 进程的组成 进程的特征 总结 2.1.2 进程的状态与转换,进程的组织 创建态、就绪态 运行态 阻塞态 终止态 进程状态的转换 进程的组织 链式方式 索引方式 2.1.3 进程控制 如何实现进程控制? 在下面的例子,将PCB2的是state设为1和和把…...

abap 可配置通用报表字段级日志监控
文章目录 1.功能需求描述1.1 功能1.2 效果展示2.数据库表解释2.1 表介绍3.数据库表及字段3.1.应用日志数据库抬头表:ZLOG_TAB_H3.2.应用日志数据库明细表:ZLOG_TAB_P3.3.应用日志维护字段配置表:ZLOG_TAB_F4.日志封装类5.代码6.调用方式代码7.调用案例程序demo1.功能需求描述 …...

OpenCV视觉分析之目标跟踪(11)计算两个图像之间的最佳变换矩阵函数findTransformECC的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 根据 ECC 标准 78找到两幅图像之间的几何变换(warp)。 该函数根据 ECC 标准 ([78]) 估计最优变换(warpMatri…...

PGMP-串串0203 项目集管理绩效域战略一致性
1.项目集管理绩效域 2.战略一致性 战略一致性包含内容商业论证BC项目集章程项目集路线图环境评估项目集风险管理策略 前期formulation sub-phaseplanning sub-phase组织的战略计划项目集风险管理策略项目集管理计划商业论证BC项目集章程项目集路线图环境评估...

HiveMetastore 的架构简析
HiveMetastore 的架构简析 Hive Metastore 是 Hive 元数据管理的服务。可以把元数据存储在数据库中。对外通过 api 访问。 hive_metastore.thrift 对外提供的 Thrift 接口定义在文件 standalone-metastore/src/main/thrift/hive_metastore.thrift 中。 内容包括用到的结构体…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
