期权懂|期权新手看过来:看跌期权该如何交易?
期权小懂每日分享期权知识,帮助期权新手及时有效地掌握即市趋势与新资讯!
期权新手看过来:看跌期权该如何交易?
一、可以直接购买看跌期权:
(1)选择预期下跌的标的资产。
(2)购买该资产的看跌期权,确定执行价格和到期日。
(3)若市场价格下跌至执行价格以下,期权增值,可选择行使或卖出期权获利。
二、保护性看跌期权:
(1)持有某股票,担心价格下跌,可购买对应股票的看跌期权作为保护。
(2)若股票价格下跌,看跌期权增值,可抵消持股损失。
三、组合策略:
(1)同时购买和卖出不同执行价格的看跌期权,如买入执行价格较低的看跌期权,卖出执行价格较高的看跌期权,适用于预期小幅下跌时。
四、卖出看跌期权:
(1)预期资产价格稳定或上涨时,可卖出看跌期权赚取期权费。
(2)但若资产价格大幅下跌,卖方将面临无限损失风险。
以上就是期权小懂分享的期权策略中两边开卖方实值对冲会有盈利区间吗?全部内容,希望本期文章能够帮到你!

相关文章:

期权懂|期权新手看过来:看跌期权该如何交易?
期权小懂每日分享期权知识,帮助期权新手及时有效地掌握即市趋势与新资讯! 期权新手看过来:看跌期权该如何交易? 一、可以直接购买看跌期权: (1)选择预期下跌的标的资产。 (2&#…...
:密码学Hash算法的分类)
《深入浅出HTTPS》读书笔记(8):密码学Hash算法的分类
密码学Hash算法有很多,比如MD5算法、SHA族类算法,MD5早已被证明是不安全的Hash算法了,目前使用最广泛的Hash算法是SHA族类算法。 1)MD5 MD5是一种比较常用的Hash算法,摘要值长度固定是128比特。 MD5算法目前被证明已…...

大语言模型安全,到底是什么的安全
什么是AI安全 自ChatGPT问世以来,市场上涌现出了众多大型语言模型和多样化的AI应用。这些应用和模型在为我们的生活带来便利的同时,也不可避免地面临着安全挑战。AI安全,即人工智能安全,涉及在人工智能系统的开发、部署和使用全过…...

论文2—《基于柔顺控制的智能神经导航手术机器人系统设计》文献阅读分析报告
论文报告:基于卷积神经网络的手术机器人控制系统设计 摘要 本研究针对机器人辅助微创手术中定向障碍和缺乏导航信息的问题,设计了一种智能控制导航手术机器人系统。该系统采用可靠和安全的定位技术、7自由度机械臂以及避免关节角度限制的逆运动学控制策…...
)
试编写算法将单链表就地逆置(默认是带头节 点,如果是不带头节点地逆置呢?)
编写一个算法来就地逆置一个单链表。默认情况下,链表是带头节点的,但如果链表不带头节点,逆置的过程会有所不同。 第一步:定义逆置函数 根据题目中的“试编写算法将单链表就地逆置”,我们需要: 定义一个…...

FPGA学习笔记#3 Vitis HLS编程规范、数据类型、基本运算
本笔记根据笔者目前的项目确定学习目标,目前主要集中在Vitis HLS上,使用的Vitis HLS版本为2022.2,在windows11下运行,仿真part为xcku15p_CIV-ffva1156-2LV-e,从这一篇开始是HLS的学习进度,主要根据教程&…...

爬虫 - 二手交易电商平台数据采集 (一)
背景: 近期有一个需求需要采集某电商网站平台的商品数据进行分析。因此,我计划先用Python实现一个简单的版本,以快速测试技术的实现可能性,再用PHP实现一个更完整的版本。文章中涉及的技术仅为学习和测试用途,请勿用于商业或非法用…...

“成交量分布指标“,通过筹码精准锁定价格方向+简单找市场支撑压力位 MT4免费公式!
指标名称:成交量分布指标 版本:MT4 ver. 1.32 之前发布的市场分布图不少朋友反馈不错,希望获得其它版本。 这个版本只有MT4的,MT5可以看之前版本,链接: “市场分布图”,精准把握价格动向 更直…...

简记Vue3(四)—— 路由
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...

Python批量合并多个PDF
在日常工作中,处理和合并多个 PDF 文件是一个常见需求,尤其是在需要将大量文件整理成一个完整文档时。本文将详细介绍如何使用 Python 的 PyMuPDF 库来实现批量 PDF 文件合并,并提供针对大文件优化的解决方案。 安装 PyMuPDF 要使用 PyMuPD…...

Linux:vim命令总结及环境配置
文章目录 前言一、vim的基本概念二、vim模式命令解析1. 命令模式1)命令模式到其他模式的转换:2)光标定位:3)其他命令: 2. 插入模式3. 底行模式4. 替换模式5. 视图模式6. 外部命令 三、vim环境的配置1. 环境…...

贪心算法day05(k次取反后最大数组和 田径赛马)
目录 1.k次取反后最大化的数组和 2.按身高排序 3.优势洗牌 1.k次取反后最大化的数组和 题目链接:. - 力扣(LeetCode) 思路: 代码: class Solution {public int largestSumAfterKNegations(int[] nums, int k) {//如…...
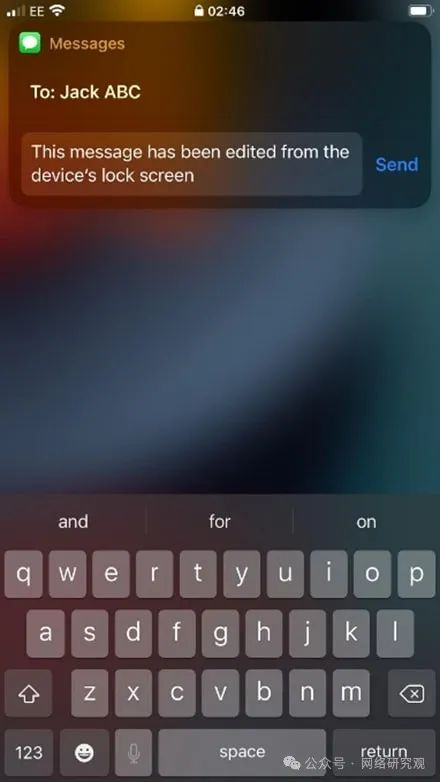
默认 iOS 设置使已锁定的 iPhone 容易受到攻击
苹果威胁研究的八个要点 苹果手机间谍软件问题日益严重 了解 Apple 苹果的设备和服务器基础模型发布 尽管人们普遍认为锁定的 iPhone 是安全的,但 iOS 中的默认设置可能会让用户面临严重的隐私和安全风险。 安全研究员 Lambros 通过Pen Test Partners透露&#…...

上海市计算机学会竞赛平台2024年11月月赛丙组
题目描述 在一个棋盘上,有两颗棋子,一颗棋子在第 aa 行第 bb 列,另一个颗棋子在第 xx 行第 yy 列。 每一步,可以选择一个棋子沿行方向移动一个单位,或沿列方向移动一个单位,或同时沿行方向及列方向各移动…...

Python批量设置图片背景为透明
我们日常生活中制作PPT等教学资源时,需要批量去除图片背景,就可以使用 Python 的 rembg 库。 这个库基于神经网络模型,去背景效果较好,可以批量处理png, jpg, jpeg等图片。采用以下代码可以批量处理当前目录下的所有图片…...

Vue CLI 脚手架
cli脚手架创建项目步骤 全局安装(一次):yarn global add vue/cli 无法识别yarn的要先安装yarn;终端执行npm install -g yarn 查看Vue版本:vue --version 这里有问题(success上方有warning) 报错:‘vue’不是内部或外部…...

Linux【基础篇】
-- 原生罪 linux的入门安装学习 什么是操作系统? 用户通过操作系统和计算机硬件联系使用。桥梁~ 什么是Linux? 他是一套开放源代码(在互联网上找到Linux系统的源代码,C语言写出的软件),可以自由 传播&…...

多线程环境下安全地使用 SimpleDateFormat的常见方法
文章目录 1. 使用局部变量(每个线程独立一个实例)2. 使用 ThreadLocal<SimpleDateFormat>3. 使用 DateTimeFormatter(Java 8 及以上)4. 使用 DateFormat 子类(如 FastDateFormat)5. 使用 synchronize…...

easyexcel实现自定义的策略类, 最后追加错误提示列, 自适应列宽,自动合并重复单元格, 美化表头
easyexcel实现自定义的策略类, 最后追加错误提示列, 自适应列宽,自动合并重复单元格, 美化表头 原版表头和表体字体美化自动拼接错误提示列自适应宽度自动合并单元格使用Easyexcel使用poi导出 在后台管理开发的工作中,离不开的就是导出excel了. 如果是简单的导出, 直接easyexce…...

ANDROIDWORLD: A Dynamic Benchmarking Environment for Autonomous Agents论文学习
这个任务是基于androidenv的。这个环境之前学过,是一个用来进行强化学习的线上环境。而这篇文章的工作就是要给一些任务加上中间的奖励信号。这种训练环境的优点就是动态,与静态的数据集(比如说我自己的工作)不同,因此…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
