AI基础知识
目录
- 1.激活函数
- :one: 激活函数的作用
- :two: sigmoid函数
- :three: tanh函数
- :four: ReLu
- :five: Leaky ReLU
- 2.Softmax函数
- 3.优化器
- :one: 优化器的作用
- :two: BGD(批梯度下降)
- :three: SGD(随机梯度下降)
- :four: MBGD(Mini Batch梯度下降)
- :five: AdaGrad(自适应学习率优化器)
- :six: RMSProp(Root Mean Square Propagation)
- :seven: Adam(Adaptive Momen Estimation,自适应动量估计)
- 4.梯度消失和爆炸
- :one: 梯度消失
- :two: 梯度爆炸
- 5.输入数据的归一化
- :one: 标准化
- :two:最小-最大归一化
- 6.神经网络层内部的归一化
- :one: 批量归一化
- :two: 层归一化
- 7.如何处理过拟合?
- :one: Dropout
- :two: 增大数据量
- :three:Early Stop。
- :four:Batch Normalization
- :five: L1正则化
- :six: L2正则化
- 8.全连接层的作用
- 9.池化
- :one: 平均池化
- :two: 最大池化
- 10.卷积的感受野
- :one:
- :two:
- :three:
- :four:
- :five:
- :six:
- :seven:
1.激活函数
1️⃣ 激活函数的作用
激活函数为神经网络引入非线性,如果没有激活函数,即使网络层数再多,也只能处理线性可分问题。
2️⃣ sigmoid函数
sigmoid函数将输入变换为(0,1)上的输出。它将范围(-inf,inf)中的任意输入压缩到区间(0,1)中,函数表示为:
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac1{1+e^{-x}} sigmoid(x)=1+e−x1

其梯度可以表示为:
d d x s i g m o i d ( x ) = e − x ( 1 + e − x ) 2 = s i g m o i d ( x ) [ 1 − s i g m o i d ( x ) ] \frac d{dx}sigmoid(x)=\frac{e^{-x}}{(1+e^{-x})^2}=sigmoid(x)[1-sigmoid(x)] dxdsigmoid(x)=(1+e−x)2e−x=sigmoid(x)[1−sigmoid(x)]

可以发现,sigmoid函数的梯度在0到0.25之间。输入很大或很小时会趋于0,当网络变得越来越深时,会出现梯度消失问题。
优点:
- 能够将自变量的值全部压缩到(0,1)之间
- 连续可导
缺点:
- 输入趋于无穷大或无穷小时会出现梯度消失问题
- 存在幂运算,计算复杂度大
3️⃣ tanh函数
tanh函数将其输入压缩转换到区间(-1,1)上,公式如下:
t a n h ( x ) = 1 − e − 2 x 1 + e − 2 x tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}} tanh(x)=1+e−2x1−e−2x

tanh函数的梯度是:
d d x t a n h ( x ) = 1 − t a n h 2 ( x ) \frac d{dx}tanh(x)=1-tanh^2(x) dxdtanh(x)=1−tanh2(x)

可以发现当输入接近0时,tanh函数的梯度接近最大值1。与sigmoid函数的梯度类似,输入在任一方向上远离0点,梯度越接近0,因此也存在梯度消失问题。
优点
- 相比于Sigmoid,tanh在输入靠近0的区域,梯度为1,有助于收敛。但输入趋于无穷大或无穷小时会出现梯度消失问题
缺点
- 和sigmoid函数一样,输入趋于无穷大或无穷小时会出现梯度消失问题
- 同样存在幂运算,计算复杂度大
4️⃣ ReLu
线性整流单元(ReLU)提供了一种非常简单的非线性变换,被定义为:
R e L u ( x ) = m a x ( x , 0 ) ReLu(x)=max(x,0) ReLu(x)=max(x,0)

其梯度可以表示为:
f ′ ( x ) = { 1 , x > 0 0 , x < 0 f^{^{\prime}}(x)=\begin{cases}1,\quad\text{x}>0\\0,\quad\text{x}<0&\end{cases} f′(x)={1,x>00,x<0

当输入为正时,ReLU函数的梯度为1;当输入值等于0时,梯度可以当成1也可以当成0,实际应用中并不影响;输入小于0时,梯度直接为0,但在神经网络训练过程中,输入小于0的神经元占比很少。因此ReLu函数可以有效缓解梯度消失问题。
优点
- 相较于sigmoid和tanh,relu在输入大于0时,梯度恒为1,不会出现梯度消失问题
- 线性函数,收敛快
缺点:
- dead relu问题:当输入小于0时,梯度为0,导致参数无法更新
5️⃣ Leaky ReLU
在小于0的部分引入一个斜率,使得小于0的取值不再是0(通常a的值为0.01左右):
f ( x ) = { a ⋅ x x <=0 x x>0 f(x)=\begin{cases}a\cdot x&\text{ x <=0}\\x&\text{ x>0}&\end{cases} f(x)={a⋅xx x <=0 x>0
其梯度可以表示为:
f ′ ( x ) = { a x <=0 1 x>0 f^{\prime}(x)=\begin{cases}a&\text{ x <=0}\\1&\text{ x>0}&\end{cases} f′(x)={a1 x <=0 x>0
优点:
- 解决了dead relu问题
缺点:
- 负斜率需要预先设定,但不同任务的斜率可能不同
2.Softmax函数
softmax函数常用于多分类任务,将输入映射成一个0到1范围的概率,且所有的输出和为1
假设输入为 z = [ z 1 , z 2 , … , z n ] z=[z_1,z_2,\ldots,z_n] z=[z1,z2,…,zn] ,Softmax 函数的输出为:
s o f t m a x ( z i ) = e z i ∑ j = 1 n e z j \mathrm{softmax}(z_i)=\frac{e^{z_i}}{\sum_{j=1}^ne^{z_j}} softmax(zi)=∑j=1nezjezi
3.优化器
1️⃣ 优化器的作用
优化器的作用是调整模型参数,以最小化损失函数
2️⃣ BGD(批梯度下降)
在更新参数时使用所有样本进行更新,假设样本总数为N:
θ ′ = θ − η ⋅ 1 N ∑ i = 1 N ∇ θ J ( θ ) \theta'=\theta-\eta\cdot\frac1N\sum_{i=1}^N\nabla_\theta J(\theta) θ′=θ−η⋅N1i=1∑N∇θJ(θ)
其中, η \eta η为学习率, ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ)是损失函数对网络参数 θ \theta θ的梯度。
优点:
- BGD得到的是一个全局最优解,
缺点:
- 每迭代一步,都要用到训练集的所有数据,如果样本数巨大,模型训练速度会很慢。
3️⃣ SGD(随机梯度下降)
SGD 是最基本的优化方法。每次更新权重时,使用一个样本或batch size个样本(多个样本则计算平均梯度)计算梯度:
参数更新公式:
θ ′ = θ − η ⋅ ∇ θ J ( θ ) \theta'=\theta-\eta\cdot\nabla_\theta J(\theta) θ′=θ−η⋅∇θJ(θ)
其中, θ \theta θ是参数, η \eta η是学习率, ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ)是损失函数对网络参数 θ \theta θ的梯度。
优点:
- 实现简单、效率高
缺点:
- 收敛速度慢,容易陷入局部最优解
4️⃣ MBGD(Mini Batch梯度下降)
介于批梯度下降和随机梯度下降之间,每次更新参数时使用b个样本。
θ ′ = θ − η ⋅ 1 b ∑ i = 1 b ∇ θ J ( θ ) \theta'=\theta-\eta\cdot\frac1b\sum_{i=1}^b\nabla_\theta J(\theta) θ′=θ−η⋅b1i=1∑b∇θJ(θ)
特点:
- 训练过程比较稳定;BGD可以找到局部最优解,不一定是全局最优解;若损失函数为凸函数,则BGD所求解一定为全局最优解。
5️⃣ AdaGrad(自适应学习率优化器)
AdaGrad优点是可以自适应学习率。该优化器在较为平缓处有比较高的学习效率,在陡峭处学习率小,在一定程度上可以避免越过极小值。
6️⃣ RMSProp(Root Mean Square Propagation)
AdaGrad算法虽然解决了学习率无法根据当前梯度自动调整的问题,但是过于依赖之前的梯度,在梯度突然变化时无法快速响应。RMSProp为了解决这一问题,在AdaGrad的基础上增加了衰减速率参数。也就是说在当前梯度与之前梯度之间添加了权重,如果当前梯度的权重较大,那么响应速度也就更快
7️⃣ Adam(Adaptive Momen Estimation,自适应动量估计)
Adam优化算法是在RMSProp的基础上增加了动量。有时候通过RMSProp优化算法得到的值不是最优解,有可能是局部最优解,引入动量的概念后,求最小值就像是一个球从高处落下,落到局部最低点时会继续向前探索,有可能得到更小的值
4.梯度消失和爆炸
1️⃣ 梯度消失
- 激活函数的特性:sigmoid和tanh在输入趋于无穷大或无穷小时会出现梯度消失问题
- 深度网络层数累计:随着层数增多,反向传播时梯度会逐层相乘,导致梯度逐渐减小
- 权重初始化不当:如果初始化权重过小,反向传播时梯度会减小,导致梯度消失
如何解决?
- 使用relu激活函数
- 使用 Batch Normalization:通过对每一层的输出进行归一化,保持输出在一个稳定的分布范围内,防止梯度逐层缩小
2️⃣ 梯度爆炸
- 深度网络层数累计:若每层的梯度稍大,梯度逐层相乘会导致梯度爆炸
- 权重初始化不当:如果初始化权重过大,反向传播时梯度会变大,导致梯度爆炸
如何解决?
- 合适的权重初始化
5.输入数据的归一化
输入数据的归一化可以使数据分布一致,加快收敛速度。
1️⃣ 标准化
将数据调整为均值为 0、标准差为1的分布:
x ′ = x − μ σ x^{\prime}=\frac{x-\mu}\sigma x′=σx−μ
其中 x x x是原始数据, μ \mu μ是数据的均值, σ \sigma σ是数据的标准差。
2️⃣最小-最大归一化
x ′ = x − min ( x ) max ( x ) − min ( x ) x^{\prime}=\frac{x-\min(x)}{\max(x)-\min(x)} x′=max(x)−min(x)x−min(x)
6.神经网络层内部的归一化
1️⃣ 批量归一化
没写
2️⃣ 层归一化
没写
7.如何处理过拟合?
1️⃣ Dropout
训练时随机丢弃部分神经元,减少神经元之间的相互依赖,迫使网络学习更加鲁邦的表示,防止过拟合。
2️⃣ 增大数据量
增大的数据量可以使模型学习到更多的特征,防止过拟合
3️⃣Early Stop。
将数据集分为训练集、验证集、测试集,每个epoch后都用验证集验证一下,如果随着训练的进行训练集Loss持续下降,而验证集Loss先下降后上升,说明出现过拟合,应该立即停止训练
4️⃣Batch Normalization
没写
5️⃣ L1正则化
没写
6️⃣ L2正则化
没写
8.全连接层的作用
- 特征融合:将前一层的所有特征融合成更高层次的特征
- 决策输出:全连接层放在网络的末端,将提取的特征映射到类别,实现分类任务
9.池化
1️⃣ 平均池化
2️⃣ 最大池化
10.卷积的感受野
1️⃣
2️⃣
3️⃣
4️⃣
5️⃣
6️⃣
7️⃣
相关文章:

AI基础知识
目录 1.激活函数:one: 激活函数的作用:two: sigmoid函数:three: tanh函数:four: ReLu:five: Leaky ReLU 2.Softmax函数3.优化器:one: 优化器的作用:two: BGD(批梯度下降):three: SGD(随机梯度下降):four: MBGD(Mini Ba…...

ubuntu 22.04 硬件配置 查看 显卡
ubuntu 22.04 硬件配置 查看 显卡 1. 参考文档 ubuntu 安装 nvidia 驱动 https://blog.51cto.com/u_13628828/7056095 input: HDA NVidia HDMI/DP,pcm3 as /devices/pci0000:00/0000:00:01.0/0000:01:00.1/sound/card1/input11 input: HDA NVidia HDMI/DP,pcm7 as /devices/…...

【计算机网络】网络框架
一、网络协议和分层 1.理解协议 什么是协议?实际上就是约定。如果用计算机语言进行表达,那就是计算机协议。 2.理解分层 分层是软件设计方面的优势(低耦合);每一层都要解决特定的问题 TCP/IP四层模型和OSI七层模型…...

linux nvidia/cuda安装
1.查看显卡型号 lspci |grep -i vga2.nvidia安装 2.1在线安装 终端输入(当显卡插上之后,系统会有推荐的安装版本) ubuntu-drivers devices可得到如下内容 vendor : NVIDIA Corporation model : TU104GL [Tesla T4] driver : nvid…...

硬件设备网络安全问题与潜在漏洞分析及渗透测试应用
以下笔记学习来自B站泷羽Sec: B站泷羽Sec 一、硬件设备的网络安全问题点 1.1 物理安全问题 设备被盗或损坏渗透测试视角 攻击者可能会物理接近硬件设备,尝试窃取设备或破坏其物理结构。例如,通过撬锁、 伪装成维修人员等方式进入设备存放…...

#渗透测试#SRC漏洞挖掘#CSRF漏洞的防御
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...

C++ | Leetcode C++题解之第542题01矩阵
题目: 题解: class Solution { public:vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {int m matrix.size(), n matrix[0].size();// 初始化动态规划的数组,所有的距离值都设置为一个很大的…...

RabbitMQ 不公平分发介绍
RabbitMQ 是一个流行的开源消息代理软件,它实现了高级消息队列协议(AMQP)。在 RabbitMQ 中,消息分发策略对于系统的性能和负载均衡至关重要。默认情况下,RabbitMQ 使用公平分发(Fair Dispatch)策…...

测试实项中的偶必现难测bug--一键登录失败
问题描述:安卓和ios有出现部分一键登录失败的场景,由于场景比较极端,衍生了很多不好评估的情况。 产生原因分析: 目前有解决过多次这种行为的问题,每次的产生原因都有所不同,这边根据我个人测试和收集复现的情况列举一些我碰到的: 1、由于我们调用的是友盟的一键登录的…...

危!这些高危端口再不知道问题就大了
号主:老杨丨11年资深网络工程师,更多网工提升干货,请关注公众号:网络工程师俱乐部 下午好,我的网工朋友。 端口作为网络通信的基本单元,用于标识网络服务和应用程序。 但某些端口由于其开放性和易受攻击的…...

Redis集群模式之Redis Sentinel vs. Redis Cluster
在分布式系统环境中,Redis以其高性能、低延迟和丰富的数据结构而广受青睐。随着数据量的增长和访问需求的增加,单一Redis实例往往难以满足高可用性和扩展性的要求。为此,Redis提供了两种主要的集群模式:Redis Sentinel和Redis Clu…...

Leetcode 罗马数字转整数
代码的算法思想可以分为以下几步: 建立映射表: 首先,代码使用 HashMap 来存储罗马数字字符与其对应的整数值关系。例如,I 对应 1,V 对应 5,以此类推。这是为了方便后续快速查找每个罗马字符对应的整数值。 …...

东方通TongWeb替换Tomcat的踩坑记录
一、背景 由于信创需要,原来项目的用到的一些中间件、软件都要逐步替换为国产品牌,决定先从web容器入手,将Tomcat替换掉。在网上搜了一些资料,结合项目当前情况,考虑在金蝶AAS和东方通TongWeb里面选择,后又…...

ceph介绍和搭建
1 为什么要使用ceph存储 什么是对象存储? 对象存储并没有向文件系统那样划分为元数据区域和数据区域,而是按照不同的对象进行存储,而且每个对象内部维护着元数据和数据区域。因此每个对象都有自己独立的管理格式。 对象存储优点:…...

树莓派安装FreeSWITCH
1、下载相关资源: # 假设所有资源都下载到/opt/目录下 cd /opt # 下载FreeSWITCH源码 git clone https://github.com/signalwire/freeswitch # 下载libks源码 git clone https://github.com/signalwire/libks # 下载sofia-sip源码 git clone https://github.com/fr…...

OpenSSL 生成根证书、中间证书和网站证书
OpenSSL 生成根证书、中间证书和网站证书 一、生成根证书(ChinaRootCA)二、生成中间 CA(GuangDongCA)三、生成网站证书(gdzwfw) 一、生成根证书(ChinaRootCA) 创建私钥: …...
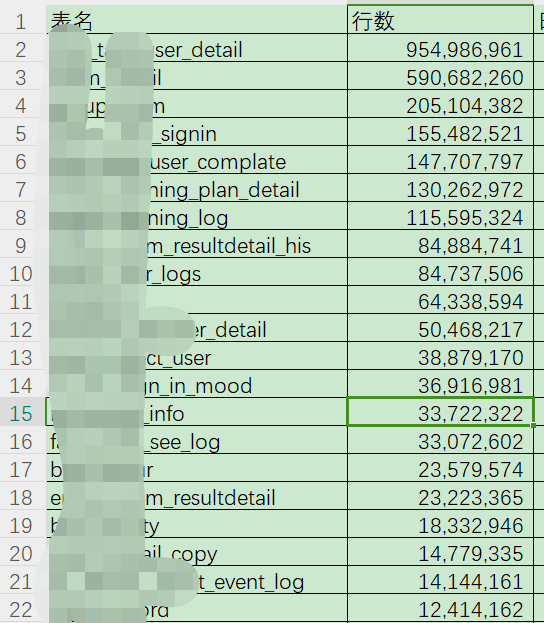
MySQL核心业务大表归档过程
记录一下2年前的MySQL大表的归档,当时刚到公司,发现MySQL的业务核心库,超过亿条的有7张表,最大的表有9亿多条,有37张表超过5百万条,部分表行数如下: 在测试的MySQL环境 : pt-archiv…...

dapp获取钱包地址,及签名
npm install ethersimport {ethers} from ethers const accounts await ethereum.request({method: eth_requestAccounts}); // 获取钱包地址 this.form.address accounts[0] console.log("accounts:" this.address)const provider new ethers.BrowserProvider(…...

探索Dijkstra算法的普遍最优性:从经典算法到最新学术突破
引言 在计算机科学中,Dijkstra算法是解决单源最短路径问题的经典算法,尤其在地图导航、网络通信和机器人路径规划等领域有着广泛应用。近期,学术界在此算法上取得了重大突破:研究人员证明了Dijkstra算法的“普遍最优性”ÿ…...

️代码的华尔兹:在 Makefile 的指尖上舞动自动化的诗篇
文章目录 😶🌫️😶🌫️😶🌫️背景——一个优秀工程师必备技能😶🌫️😶🌫️😶🌫️一、🤩🤩快速了解…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
