LeetCode --- 143周赛
题目列表
3345. 最小可整除数位乘积 I
3346. 执行操作后元素的最高频率 I
3347. 执行操作后元素的最高频率 II
3348. 最小可整除数位乘积 II
一、最小可整除数位成绩I

由于本题的数据范围比较小,我们直接暴力枚举即可,代码如下
class Solution {
public:int smallestNumber(int n, int t) {// 最多循环 10 次,一定能遇到一个带 0 的数字for(int i = n; ; i++){ int tmp = i;int res = 1;while(tmp){res *= (tmp % 10);tmp /= 10;}if(res % t == 0)return i;}return -1;}
};二、执行操作后元素的最高频率 I & II

在numOperations的操作内,求出现频率最高的数字的出现次数。我们可以先计算出对于任意一个数,在不考虑操作次数的情况下,最多有多少个数字能变成它,然后与操作次数求min,再加上该数字本身出现的个数即可,如何计算有多少个数字能变成它?这比较难算,我们可以换一个角度,对于给定的数字,它能变成哪些数字,我们是很容易求出的,而且它能变成的数字是一个区间,并且我们只要计算频率,所以只要对区间整体进行+1/-1的操作即可,很明显,用差分数组进行计算

由于本题的加强版数据范围太大,开数组会爆内存,所以用map来代替数组,map中记录出现变化的点的频率,这样那些频率不发生变化的点就不用遍历了,也大大降低了时间复杂度 ,代码如下
class Solution {
public:int maxFrequency(vector<int>& nums, int k, int numOperations) {int n = nums.size();unordered_map<int,int> cnt; // 统计数字出现次数// 由于数据范围太大,差分数组可以用 map 来代替,节省空间map<int,int> mp; // 统计有多少个数字能变成 yfor(auto x : nums){// 对于数字 x ,能变成 [x-k, x+k] 的任意一个数,但是变成本身不需要操作次数mp[x - k]++;mp[x]--; // 对于 x 本身来说,不需要进行操作mp[x + 1]++;mp[x + k + 1]--;cnt[x]++;}int ans = 0, pre = 0;for(auto [x, c] : mp){pre += c;ans = max(ans, min(pre, numOperations) + (cnt.count(x) ? cnt[x] : 0));}return ans;}
};这题还有另外的空间复杂度为O(1)的解法。整体思路依旧不变:先计算出对于任意一个数,在不考虑操作次数的情况下,最多有多少个数字能变成它,关键在于我们需要正面解决如何计算有多少个数字能变成它?如何做?
首先,由于操作性质,肯定是相邻的数字更容易变成我们需要的数字,所以先将数组排序。然后我们将频率可能最大的数字分为两类:1、在 nums 数组中的数字 2、不在 nums 数组中的数字
- 对于在 nums 中的数字 x ,我们可以通过二分计算出 [x-k,x+k] 中的数字个数 / 通过三指针计算出 [x-k,x+k] 中的数字,同时要统计 x 出现的次数 cnt[x],从而计算频率 min(right - left, numOperations + cnt[x]),其中 [left,right) 是在 [x-k,x+k] 内的数字下标区间
- 对于不在 nums 中的数字, 我们只要维护以 x = nums[i] 为右端点的区间 [x - 2k,x] 内的数字个数即可,可以用滑动窗口计算

- 注意:一旦在 nums 数组中的数字的频率>= numOperations,直接返回即可,因为不在 nums 数组中的数字的频率最多是 numOperations
代码如下
class Solution {
public:int maxFrequency(vector<int>& nums, int k, int numOperations) {int n = nums.size();ranges::sort(nums);int l = 0, r = 0, ans = 0, cnt = 0;for(int i = 0; i < n; i++){int x = nums[i];cnt++;if(i < n - 1 && x == nums[i + 1])continue;while(r < n && nums[r] - nums[i] <= k)r++;while(nums[i] - nums[l] > k)l++;// [l, r)ans = max(ans, min(r - l, cnt + numOperations));cnt = 0;}if(ans >= numOperations) return ans;// [x-2k, x]for(int left = 0, right = 0; right < n; right++){while(nums[right] - nums[left] > 2*k)left++;ans = max(ans, right - left + 1);}return min(ans, numOperations); // 操作次数最大为numOperations}
};三、最小可整除数位成绩 II

从小到大去枚举构造所有可能的结果,代码如下
class Solution {
public:string smallestNumber(string s, long long t) {long long tmp = t;for (int i = 9; i > 1; i--) { // 本质只要枚举 2 3 5 7 即可while (tmp % i == 0) {tmp /= i;}}if (tmp > 1) { // t 包含大于 7 的质因子,即有大于 10 的因子return "-1";}int n = s.length();vector<long long> left_t(n + 1); // 从左往右,记录在保持[0, i)不变的情况下,t剩余的值left_t[0] = t;int i0 = n - 1;for (int i = 0; i < n; i++) {if (s[i] == '0') { // 如果出现 0,则 [i, n) 的数字可以任意填写i0 = i;break;}left_t[i + 1] = left_t[i] / gcd(left_t[i], s[i] - '0');}if (left_t[n] == 1) { // s 的数位之积是 t 的倍数return s;}// 假设答案和 s 一样长// 思路:在保持高位不变的情况下,尽可能的将 大数字 放在低位for (int i = i0; i >= 0; i--) {while (++s[i] <= '9') {long long tt = left_t[i] / gcd(left_t[i], s[i] - '0'); // [i,n)需要让 tt 变为 1int k = 9; // 倒着枚举,尽量让大数字在低位for (int j = n - 1; j > i; j--) {while (tt % k) {k--;}tt /= k;s[j] = '0' + k;}if (tt == 1) {return s;}}}// 答案一定比 s 长,则将 t 中的因子从大到小,依次放在个位,十位...,少的位置补1string ans;for (int i = 9; i > 1; i--) {while (t % i == 0) {ans += '0' + i;t /= i;}}ans += string(max(n + 1 - (int) ans.length(), 0), '1');ranges::reverse(ans);return ans;}
};相关文章:

LeetCode --- 143周赛
题目列表 3345. 最小可整除数位乘积 I 3346. 执行操作后元素的最高频率 I 3347. 执行操作后元素的最高频率 II 3348. 最小可整除数位乘积 II 一、最小可整除数位成绩I 由于本题的数据范围比较小,我们直接暴力枚举即可,代码如下 class Solution { p…...

[AI] 【提高认知】自动翻译技术的演变:从规则系统到深度学习的崛起
机器自动翻译 (MT) 是人工智能历史上最早的应用之一,尤其是在英语和俄语之间的翻译应用。自诞生以来,自动翻译技术从符号系统逐步演化到依赖大数据和深度学习的先进模型。本文将深入探讨机器翻译的早期方法、统计方法和现代神经网络方法的演变过程,帮助大家了解自动翻译技术…...

python机器人Agent编程——多Agent框架的底层逻辑(上)
目录 一、前言二、两个核心概念2.1 Routines(1)清晰的Prompt(2)工具调用json schema自动生成(3)解析模型的toolcall指令(4)单Agent的循环决策与输出 PS.扩展阅读ps1.六自由度机器人相…...

渑池县中药材产业党委莅临河南广宇企业管理集团有限公司参观交流
11月14日,渑池县人大副主任、工商联主席杨航率县中药材产业党委代表团一行13人,莅临河南广宇集团参观交流。河南广宇集团总经理王峰、副总经理王培等领导热情接待并陪同参观、座谈。 代表团一行首先参观了集团旗下郑州美信中医院(庚贤堂中医药…...

学习日志011--模块,迭代器与生成器,正则表达式
一、python模块 在之前学习c语言时,我们学了分文件编辑,那么在python中是否存在类似的编写方式?答案是肯定的。python中同样可以实现分文件编辑。甚至还有更多的好处: 提高代码的可维护性:当代码被分成多个文件时…...

ChatGPT 搜索 vs Google 搜索
原文:Amanda Caswell - 2024.11.01 随着 OpenAI 推出的实时搜索功能,ChatGPT 正在逐步成为像 Google 这样的传统搜索引擎的竞争对手。ChatGPT 以其对话式的回答方式而闻名,它能够在没有广告干扰的情况下提供实时的上下文信息。 我迫不及待地…...

一文简单了解Android中的input流程
在 Android 中,输入事件(例如触摸、按键)从硬件传递到应用程序并最终由应用层消费。整个过程涉及多个系统层次,包括硬件层、Linux 内核、Native 层、Framework 层和应用层。我们将深入解析这一流程,并结合代码逐步了解…...

【MySQL】SQL语言
【MySQL】SQL语言 文章目录 【MySQL】SQL语言前言一、SQL的通用语法二、SQL的分类三、SQLDDLDMLDQLDCL 总结 前言 本篇文章将讲到SQL语言,包括SQL的通用语法,SQL的分类,以及SQL语言的DDL,DML,DQL,DCL。 一、SQL的通用语法 在学习具体的SQL语句之前,先来…...

5.4.2-1 编写Java程序在HDFS上创建文件
本次实战涉及使用Java操作Hadoop HDFS,包括创建文件、判断文件存在性及异常处理。通过手动添加依赖、启动HDFS服务,成功在HDFS上创建和检查文件。进一步探索了文件操作的最佳实践,如检查文件存在性以避免重复创建,以及处理HDFS安全…...
)
The 3rd Universal CupStage 15: Chengdu, November 2-3, 2024(2024ICPC 成都)
Problem L. Recover Statistics 题目意思: 给定a, b, c三个值,确保构造的数列中包含满足题目的数量 解题思路: 100 中 选择a 50个, b45个, c4个。 #include <iostream>using namespace std;using ll long …...

显示微服务间feign调用的日志
第一步 package com.niuniu.common.config;import com.niuniu.common.CommonConstant; import com.niuniu.common.utils.UserContext; import feign.Logger; import feign.RequestInterceptor; import feign.RequestTemplate; import org.springframework.context.annotation.…...

SOHO场景开局(小型,多子网):AP+管理型交换机+路由器+光猫
业务需求 1. 实现除光猫外,整网设备通过APP进行开局,开局部署完成后,能够通过APP远程运维。 2. 需要单独划分访客、办公、视频监控3个子网,其中访客子网供顾客无线上网使用,办公子网用于接入无线和有线办公终端&#x…...
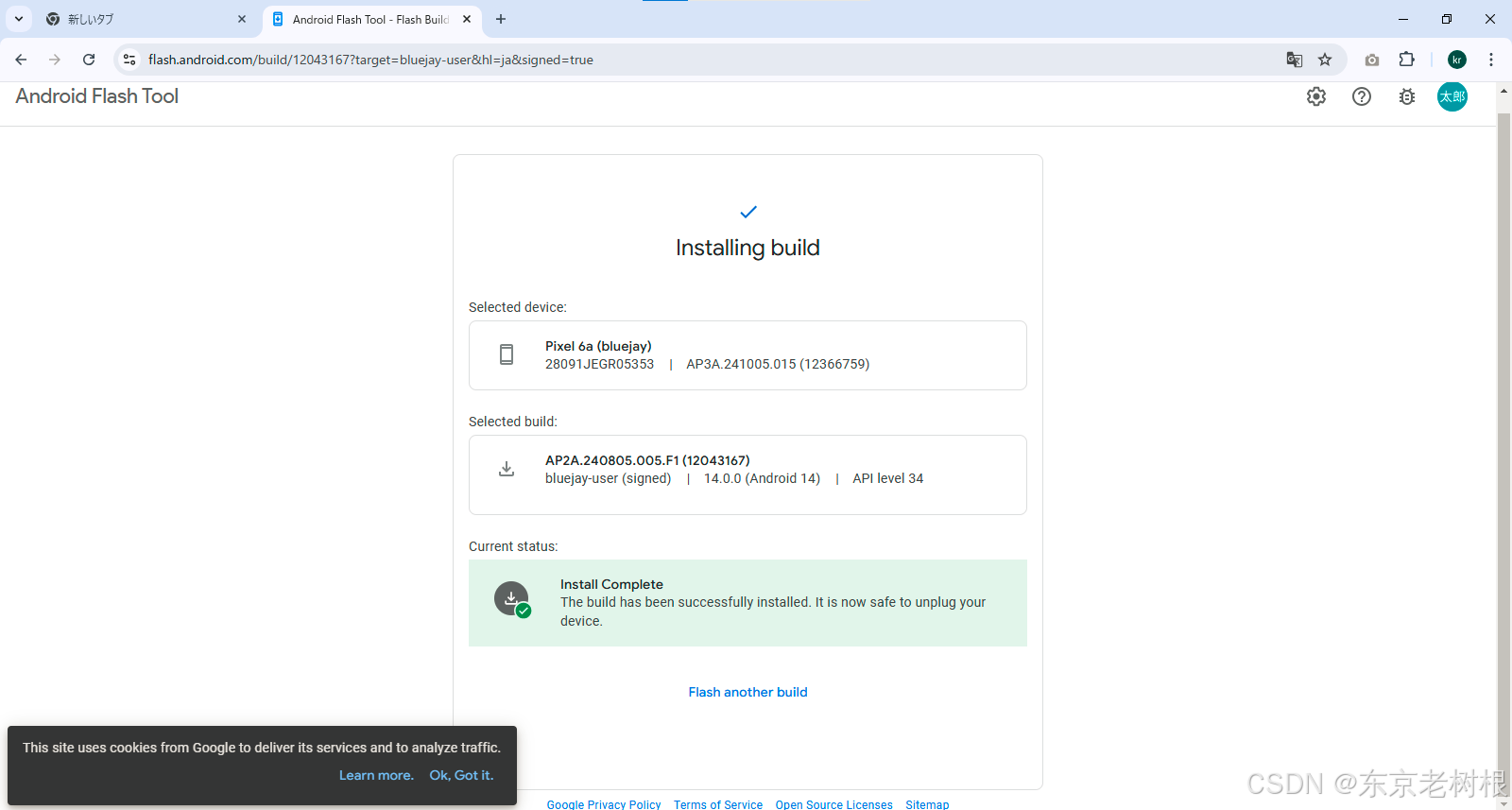
Android - Pixel 6a 手机OS 由 Android 15 降级到 Android 14 操作记录
Pixel 6a 手机由 Android 14 升级到 Android 15了,但是由于一些原因又想降级回 Android 14, 能降吗?该怎么降级呢?本篇文章来记述实际操作过程,希望能给想做相同操作的人一些帮助。 答案当然是能降,而且我…...

linux系统kkFileView 配置https预览文件
思路: 1.kkfile的 context全局路径可以修改 context-path,比如:server.servlet.context-path 2.使用nginx反向代理 /kkfile 转发到 kkfile路径上 官网教程 kkFileView - 在线文件预览 1、配置config/application.properties. server.se…...

stm32——通用定时器时钟知识点
(该图来自小破站 铁头山羊老师的stm32标准库教学)...

前端无感刷新token
摘要: Axios 无感知刷新令牌是一种在前端应用中实现自动刷新访问令牌(access token)的技术,确保用户在进行 API 请求时不会因为令牌过期而中断操作 目录概览 XMLHttpRequestAxiosFetch APIJQuni.request注意事项: 访问…...

针对股票评论的情感分类器
🏡作者主页:点击! 🤖编程探索专栏:点击! ⏰️创作时间:2024年11月16日13点39分 神秘男子影, 秘而不宣藏。 泣意深不见, 男子自持重, 子夜独自沉。 论文链接 点击开启你的论文编程之旅…...

Day18 Nim游戏
你和你的朋友,两个人一起玩 Nim 游戏: 桌子上有一堆石头。 你们轮流进行自己的回合, 你作为先手 。 每一回合,轮到的人拿掉 1 - 3 块石头。 拿掉最后一块石头的人就是获胜者。 假设你们每一步都是最优解。请编写一个函数ÿ…...
理解反射,学会反射:撬开私有性质(private)的属性与方法
看到这句话的时候证明:此刻你我都在努力 加油陌生人 个人主页:Gu Gu Study专栏:用Java学习数据结构系列喜欢的一句话: 常常会回顾努力的自己,所以要为自己的努力留下足迹喜欢的话可以点个赞谢谢了。作者:小…...
Redis在高性能缓存中的应用
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 Redis在高性能缓存中的应用 Redis在高性能缓存中的应用 Redis在高性能缓存中的应用 引言 Redis 概述 定义与原理 发展历程 Redi…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
