vue路由的钩子函数?
在 Vue 中,路由的钩子函数可以用来在导航过程中执行一些操作,比如进行权限验证、页面加载前后的处理等。常用的路由钩子函数包括全局前置守卫、全局解析守卫、全局后置钩子以及路由独享守卫。下面是这些路由守卫函数的简要说明:
- 全局前置守卫:
beforeEach(to, from, next):在路由切换开始时被调用,可以用来进行全局的导航守卫,如权限验证等。调用 next() 继续导航,调用 next(false) 中止导航,调用 next('/path') 跳转到新的路径
- 全局解析守卫:
beforeResolve(to, from, next):在导航被确认之前和所有组件内守卫和异步路由组件被解析之后调用。
- 全局后置钩子:
afterEach(to, from):在导航完成之后被调用,无法控制导航行为,通常用于页面埋点等操作。
- 路由独享守卫:
在路由配置中定义 beforeEnter(to, from, next) 函数,用于单个路由的导航守卫:
const router = new VueRouter({routes: [{path: '/profile',component: Profile,beforeEnter: (to, from, next) => {// 路由独享守卫逻辑if (isAuthenticated) {next();} else {next('/login');}}}]
});router.beforeEach((to, from, next) => {// 全局前置守卫逻辑if (to.meta.requiresAuth && !isAuthenticated) {next('/login');} else {next();}
});以上是一些常用的路由钩子函数,通过合理使用这些钩子函数可以实现更灵活的路由控制和管理。详细的用法和更多选项可以查阅 Vue Router 的官方文档。
相关文章:

vue路由的钩子函数?
在 Vue 中,路由的钩子函数可以用来在导航过程中执行一些操作,比如进行权限验证、页面加载前后的处理等。常用的路由钩子函数包括全局前置守卫、全局解析守卫、全局后置钩子以及路由独享守卫。下面是这些路由守卫函数的简要说明: 全局前置守卫…...

【Java】枚举类映射
在数据库中常用数字来代替字符串类型,编写一个枚举映射类 当数据库的介质类型要存储数字,前端可以任意传参,通过枚举转换后端都会转成数字对应类型 import lombok.Getter;/*** <p>* 存档介质类型* </p>** author Jyang* date 2…...
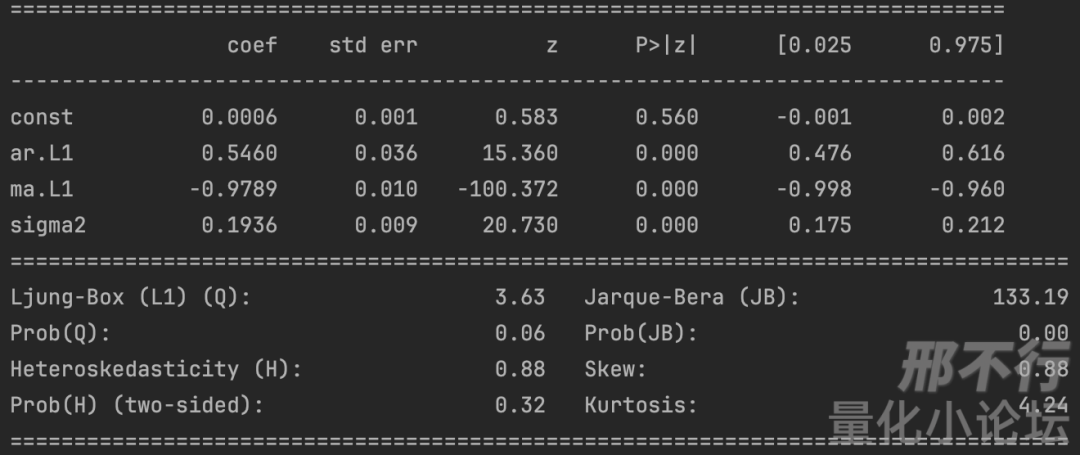
精华帖分享|浅谈金融时间序列分析与股价随机游走
本文来源于量化小论坛公共讨论区板块精华帖,作者为正扬,发布于2024年6月3日。 以下为精华帖正文: 01 引 时间序列分析是个很唬人的术语,实际上它也不是一个很容易接近的话题。我本科曾经短暂地学过一点点,又看到互联…...

任意文件下载漏洞
1.漏洞简介 任意文件下载漏洞是指攻击者能够通过操控请求参数,下载服务器上未经授权的文件。 攻击者可以利用该漏洞访问敏感文件,如配置文件、日志文件等,甚至可以下载包含恶意代码的文件。 这里再导入一个基础: 你要在网站下…...

LeetCode 445.两数相加 II
题目: 给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。 你可以假设除了数字 0 之外,这两个数字都不会以零开头。 思路:反转链表 两数相加 I 代码&…...

CentOS 7中查找已安装JDK路径的方法
使用yum安装了jdk8,但是其他中间件需要配置路径的时候,却没办法找到,如何获取jdk路径: 一、确认服务器是否存在jdk java -version 二、查找jdk的 java 命令在哪里 which java 三、找到软链指向的地址 ls -lrt /usr/bin/java l…...

springboot基于Web足球青训俱乐部管理后台系统开发(代码+数据库+LW)
摘 要 随着社会经济的快速发展,人们对足球俱乐部的需求日益增加,加快了足球健身俱乐部的发展,足球俱乐部管理工作日益繁忙,传统的管理方式已经无法满足足球俱乐部管理需求,因此,为了提高足球俱乐部管理效率…...

RHCE的学习(21)
第三章 Shell条件测试 用途 为了能够正确处理Shell程序运行过程中遇到的各种情况,Linux Shell提供了一组测试运算符。 通过这些运算符,Shell程序能够判断某种或者几个条件是否成立。 条件测试在各种流程控制语句,例如判断语句和循环语句中…...

Ubuntu 18.04 配置sources.list源文件(无法安全地用该源进行更新,所以默认禁用该源)
如果你 sudo apt update 时出现诸如 无法安全地用该源进行更新,所以默认禁用该源 的错误,那就换换源吧,链接: https://mirror.tuna.tsinghua.edu.cn/help/ubuntu/ 注意版本: 修改源文件: sudo nano /etc…...

19.UE5道具掉落
2-21 道具掉落,回血、回蓝、升级提升伤害_哔哩哔哩_bilibili 目录 1.道具的创建,道具功能的实现 2.随机掉落 1.道具的创建,道具功能的实现 新建Actor蓝图,并命名为道具总类,添加一个Niagara粒子组件和一个碰撞箱bo…...

MySQL —— MySQL逻辑架构与查询过程
文章目录 MySQL逻辑架构整体分为三层连接层服务层查询缓存解析器优化器执行器 存储引擎层系统文件层 MySQL 查询过程查询过程框图 博客1 博客2 MySQL逻辑架构整体分为三层 最上层为客户端层,并非MySQL所独有,诸如:连接管理、授权认证、权限校…...

ODOO学习笔记(12):自定义模块开发
一、Odoo模块结构基础 基本目录结构 Odoo自定义模块通常有一个特定的目录结构。一个典型的模块目录包含以下文件和文件夹: __init__.py:这是一个Python模块初始化文件。它使得该目录被视为一个Python模块。在这个文件中,你可以通过from. impo…...

Excel单元格中自适应填充多图
实例需求:在Excel插入图片时,由于图片尺寸各不相同,如果希望多个图片填充指定单元格,依靠用户手工调整,不仅费时费力,而且很难实现完全填充。如下图中的产品图册,有三个图片,如下图所…...

20.useMediaQuery
React useMediaQuery 钩子:如何优雅地实现响应式设计? 在现代 Web 开发中,响应式设计是一个关键概念,它允许应用根据不同的屏幕尺寸和设备特性调整其布局和行为。useMediaQuery 钩子提供了一种声明式的方法来在 React 组件中使用媒体查询,使得响应式逻辑的实现变得简单而…...

无人机场景 - 目标检测数据集 - 车辆检测数据集下载「包含VOC、COCO、YOLO三种格式」
数据集介绍:无人机场景车辆检测数据集,真实场景高质量图片数据,涉及场景丰富,比如无人机场景城市道路行驶车辆图片、无人机场景城市道边停车车辆图片、无人机场景停车场车辆图片、无人机场景小区车辆图片、无人机场景车辆遮挡、车…...

聚合查询(查询)
count:统计表中所有的行数 指定某一列不统计NULL sum:求和 NULL值不参与计算(省略) avg():对所有行的指定列求平均值 max() min():求所有指定行中最大值与最小值 分组查询 group by: ROUDN()小数点 havin…...

QT QLineEdit失去焦点事件问题与解决
本文介绍如何获得QLineEdit的失去焦点事件和获得焦点的输入框也会触发失去焦点事件的问题! 目录 一、QLineEdit获得失去焦点事件 1.自定义类继承自QLineEdit 2.重写 focusOutEvent 3.使用 二、失去焦点事件问题 1.问题描述 2.问题解决 三、源码分享 lineed…...

Remora
Remora Remora 模型能够独立于碱基识别过程预测甲基化/修饰碱基的状态。Remora 仓库专注于准备修饰碱基训练数据和训练修饰碱基模型。此外,还提供了一些用于运行 Remora 模型和调查原始信号的功能。对于生产环境中的修饰碱基识别,建议使用 Dorado <https://github.com/na…...

MySQL中将一个字符串字段按层级树状展开
水善利万物而不争,处众人之所恶,故几于道💦 文章目录 需求1.分析2.实现3.思路刨析表结构和数据 需求 数据库中有个字段如下 如何将其转换为如下形式: 1.分析 1.他的层级个数是不确定的,也就是说有的有2层有的有5…...

vue面试题8|[2024-11-14]
问题1:什么是渐进式框架? vue.js router vuex element ...插件 vue.js 渐0 router 渐1 vuex 渐2 vue.js只是一个核心库,比如我再添加一个router或者vuex,不断让项目壮大,就是渐进式框…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

Gitlab + Jenkins 实现 CICD
CICD 是持续集成(Continuous Integration, CI)和持续交付/部署(Continuous Delivery/Deployment, CD)的缩写,是现代软件开发中的一种自动化流程实践。下面介绍 Web 项目如何在代码提交到 Gitlab 后,自动发布…...

盲盒一番赏小程序:引领盲盒新潮流
在盲盒市场日益火爆的今天,如何才能在众多盲盒产品中脱颖而出?盲盒一番赏小程序给出了答案,它以创新的玩法和优质的服务,引领着盲盒新潮流。 一番赏小程序的最大特色在于其独特的赏品分级制度。赏品分为多个等级,从普…...
