LeetCode螺旋矩阵
快一个月没刷题了,最近工作有些忙,今天闲下来两小时,刷一道
题目描述
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:

输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
解题思路
控制上下边界、左右边界。每一次循环走一圈,走完一圈上下左右边界往内部压缩。结束条件是left>right top>bottom
- 首先初始化上边界为第0行,下边界为最后一行,左边界是第0列,右边界是最后一列。可以看出边界就是要加到res(返回数组)的一圈。
- 接下来一个循环,条件是true(无限循环),虽然终止条件是
left>right top>bottom,但是在走一圈的过程中就可能会触发终止条件,而不是一圈结束了才会触发终止条件。因此在遍历四个时,每遍历一个边就判断一次终止条件
代码
var spiralOrder = function(matrix) {let left = 0; // 初始化左边界为第0列let right = matrix[0].length-1; // 初始化右边界为最后一列let top = 0; // 初始化上边界为第0行let bottom = matrix.length-1; // 初始化下边界为最后一行let res = []; // 初始化结果数组,用于存储最终的螺旋顺序元素while(true){ // 开始一个无限循环for(let i=left;i<=right;i++){ // 从左到右遍历第一行res.push(matrix[top][i]); // 将第一行的元素添加到结果数组}top++; // 遍历完第一行后,上边界下移if(top>bottom)break; // 如果上边界超过了下边界,结束循环for(let i=top;i<=bottom;i++){ // 从上到下遍历最后一列res.push(matrix[i][right]); // 将最后一列的元素添加到结果数组}right--; // 遍历完最后一列后,右边界左移if(right<left)break; // 如果右边界小于左边界,结束循环for(let i=right;i>=left;i--){ // 从右到左遍历最后一行res.push(matrix[bottom][i]); // 将最后一行的元素添加到结果数组}bottom--; // 遍历完最后一行后,下边界上移if(bottom<top) break; // 如果下边界小于上边界,结束循环for(let i=bottom;i>=top;i--){ // 从下到上遍历第一列res.push(matrix[i][left]); // 将第一列的元素添加到结果数组}left++; // 遍历完第一列后,左边界右移if(left>right) break; // 如果左边界超过了右边界,结束循环}return res; // 返回结果数组
};
案例分析
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
逐步分析:
-
初始化边界:
left = 0right = 2top = 0bottom = 2
-
第一次循环:
- 从左到右遍历第一行(
top行):[1, 2, 3]添加到resres = [1, 2, 3]
top++(top = 1)- 检查边界:
top <= bottom(1 <= 2),继续。
- 从左到右遍历第一行(
-
第二次循环:
- 从上到下遍历最后一列(
right列):[6, 9]添加到resres = [1, 2, 3, 6, 9]
right--(right = 1)- 检查边界:
right >= left(1 >= 0),继续。
- 从上到下遍历最后一列(
-
第三次循环:
- 从右到左遍历最后一行(
bottom行):[8, 7]添加到resres = [1, 2, 3, 6, 9, 8, 7]
bottom--(bottom = 1)- 检查边界:
bottom >= top(1 >= 1),继续。
- 从右到左遍历最后一行(
-
第四次循环:
- 从下到上遍历第一列(
left列):[4]添加到resres = [1, 2, 3, 6, 9, 8, 7, 4]
left++(left = 1)- 检查边界:
left <= right(1 <= 1),继续。
- 从下到上遍历第一列(
-
第五次循环:
- 从左到右遍历第二行(
top行):[5]添加到resres = [1, 2, 3, 6, 9, 8, 7, 4, 5]
top++(top = 2)- 检查边界:
top > bottom(2 > 1),循环结束。
- 从左到右遍历第二行(
结论:
循环在第五次遍历后结束,因为此时 top > bottom 的条件满足。因此,最终结果数组 res 为 [1, 2, 3, 6, 9, 8, 7, 4, 5]。
相关文章:

LeetCode螺旋矩阵
快一个月没刷题了,最近工作有些忙,今天闲下来两小时,刷一道 题目描述 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4…...

第十五届蓝桥杯JAVA的B组题目详情解析
(第一个填空太简单,就不写了,根本不用代码,直接excel计算) 目录 蓝桥杯第二个填空,类斐波那契循环数 蓝桥杯JAVA.b组第三题 -分布式队列(模拟) 食堂(蓝桥杯D题) 编辑 星际旅行(Floyd佛洛依德) 其余的有点变态,感觉学了好像…...

在几分钟内将数据从 Oracle 迁移到 ClickHouse
ClickHouse 是一个开源的面向列的数据库管理系统。它在实时数据处理方面的出色性能显着增强了数据分析和业务洞察力。将数据从 Oracle 迁移到 ClickHouse 可以释放数据在决策中的力量,这是单独使用 Oracle 无法实现的。 本教程介绍如何使用 BladePipe 将数据从 Orac…...

ASP.NET MVC宠物商城系统
该系统采用B/S架构,使用C#编程语言进行开发,以ASP.NET MVC框架为基础,以Visual Studio 2019为开发工具,数据库采用SQL Server进行保存数据。系统主要功能包括登录注册、宠物展示、个人中心、我的订单、购物车、用户管理、宠物类别…...

完整http服务器
目录 背景目标描述技术特点开发环境WWW客户端浏览发展史服务端http发展史http分层概览 背景 http协议被广泛使用,从移动端,pc浏览器,http无疑是打开互联网应用窗口的重要协议,http在网络应用层中的地位不可撼动,是能…...
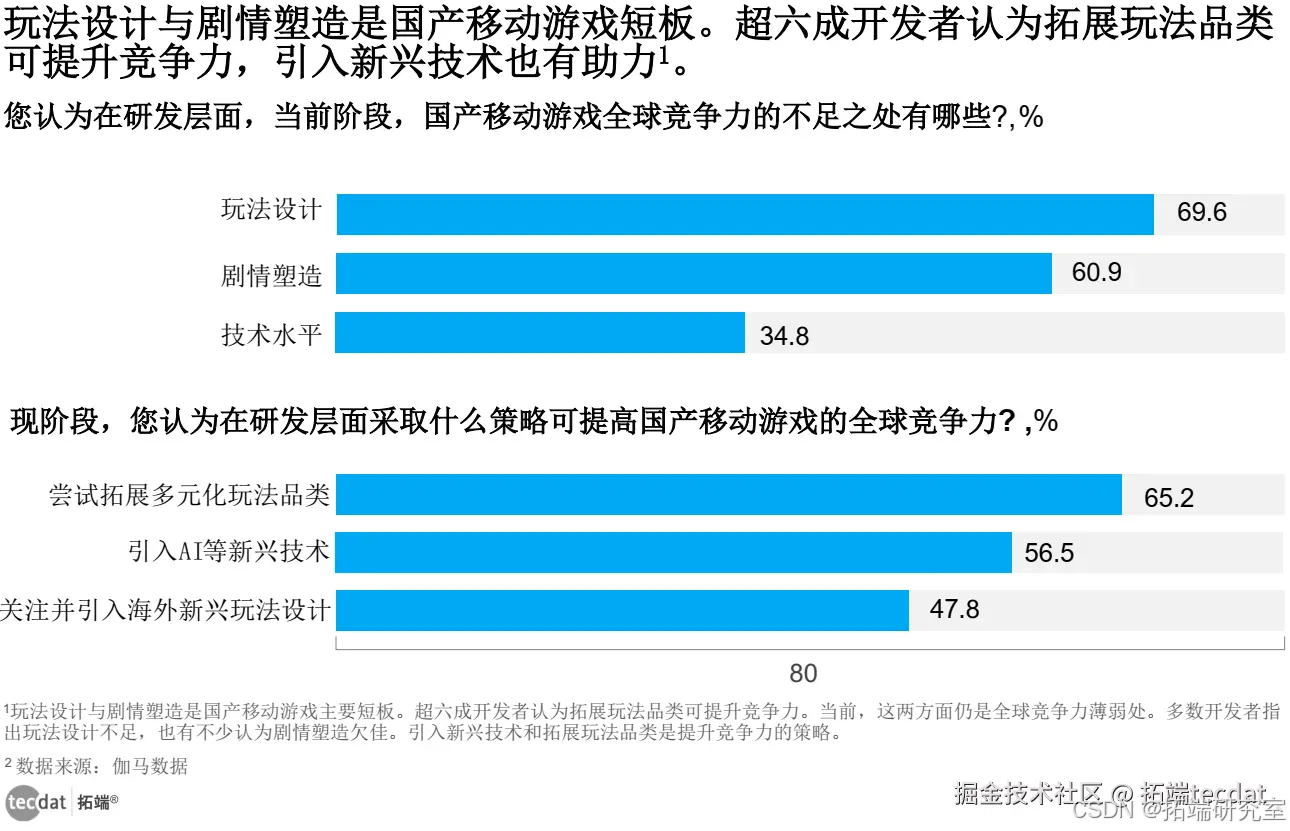
【专题】2024AIGC创新应用洞察报告汇总PDF洞察(附原数据表)
原文链接:https://tecdat.cn/?p38310 在科技日新月异的今天,人工智能领域正以前所未有的速度发展,AIGC(人工智能生成内容)成为其中最耀眼的明珠。从其应用场景的不断拓展,到对各行业的深刻变革࿰…...
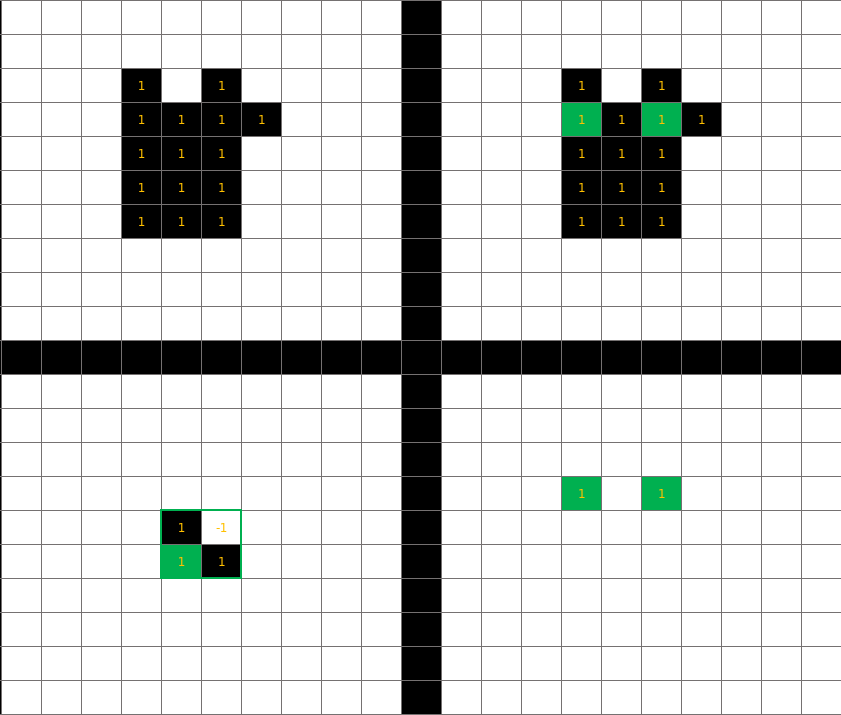
形态学图像处理(Morphological Image Processing)
形态学图像处理(Morphological Image Processing) 前言 本博客为个人总结数字图像处理一课所写,并给出适当的扩展和相应的demo。 写博客跟做 checkpoint 很像,毕竟个人还不能达到那种信手拈来的境界,忘了就是从零开始训练࿰…...

【IDER、PyCharm】免费AI编程工具完整教程:ChatGPT Free - Support Key call AI GPT-o1 Claude3.5
文章目录 CodeMoss 简介CodeMoss 的模型集成如何安装和配置 CodeMossIDER 插件安装步骤 CodeMoss 的实战使用AI 问答功能代码优化与解释优化这段代码解释这段代码 文件上传与对话联网查询与 GPT 助手联网查询GPT 助手 提升开发效率的最佳实践结语更多文献 CodeMoss 简介 CodeM…...

C++11的一些实用特性
1.统一的列表初始化 在C98中,标准允许使用花括号{}对数组或者结构体元素进行统一的列表初始值设定。 //统一的列表初始化 struct Date {int year;int month;int day; };void test1() {Date d1 { 2024,11,14 };int array1[] { 1, 2, 3, 4, 5 };int array2[5] { …...

23种设计模式-观察者(Observer)设计模式
文章目录 一.什么是观察者模式?二.观察者模式的结构三.观察者模式的应用场景四.观察者模式的优缺点五.观察者模式的实现(C示例)六.观察者模式的实现(JAVA示例)七.代码解释八.总结 类图: 观察者设计模式类图…...

【CUDA】Branch Divergence and Unrolling Loop
目录 一、避免分支发散 1.1 并行规约问题 1.2 并行规约中的发散 二、UNrolling Loops 一、避免分支发散 控制流有时依赖于 thread 索引。同一个warp中,一个条件分支可能导致性能很差。通过重新组织数据获取模式可以减少或避免 warp divergence。具体问题查看下…...

深度学习:卷积神经网络的计算复杂度,顺序操作,最大路径长度
卷积层的计算复杂度 在深度学习中,卷积层的计算复杂度主要取决于卷积核的大小、输入和输出的通道数量、以及输入序列的长度。具体来说,卷积层的计算复杂度可以通过以下几个因素来计算: 卷积核大小 k:卷积核的大小决定了每次卷积操…...

springboot 配置文件中 multipart.max-file-size 各个版本的写法
由于springboot具有几个版本,不同版本对于文件上传最大限制的配置也有所不同。 所以要注意springboot本身的版本,不然会一直报错 在springboot1.3版本中: multipart.maxFileSize在springboot1.4与springboot1.5版本中: spring…...

linux 中mysql查看慢日志
1、到mysql容器,先登录到数据库,查看是否开启 mysql -h 127.0.0.1 -uroot -p SHOW VARIABLES LIKE slow_query_log; 2、如果没有开启,需要先开启 set global slow_query_log ON; 3、查看慢日志文件 SHOW VARIABLES LIKE slow_query_log…...

单片机的基本组成与工作原理
单片机(Microcontroller Unit, MCU)是一种将计算机的主要部分集成在一个芯片上的小型计算机系统。它通常包括中央处理器(CPU)、存储器(Memory)、输入输出接口(I/O Ports)、定时器/计…...

智慧隧道和智慧交通
通过引入先进的物联网技术,将各种硬件设备如传感器、摄像头、控制系统等有效地连接并管理起来,以实现道路安全和交通流畅的目标。这些设备将能够实时监控和控制隧道内的各种设备和系统,从而提高道路安全、提升驾驶体验并降低管理成本。 在这个…...

List、Set、Map详解和区别
在 Java 中,List、Set、Map是常用的集合类型,它们各自具有不同的特点和用途,以下是对它们的详细介绍及区别分析: List(列表) 特点: 有序性:List中的元素是有序的,即元素…...
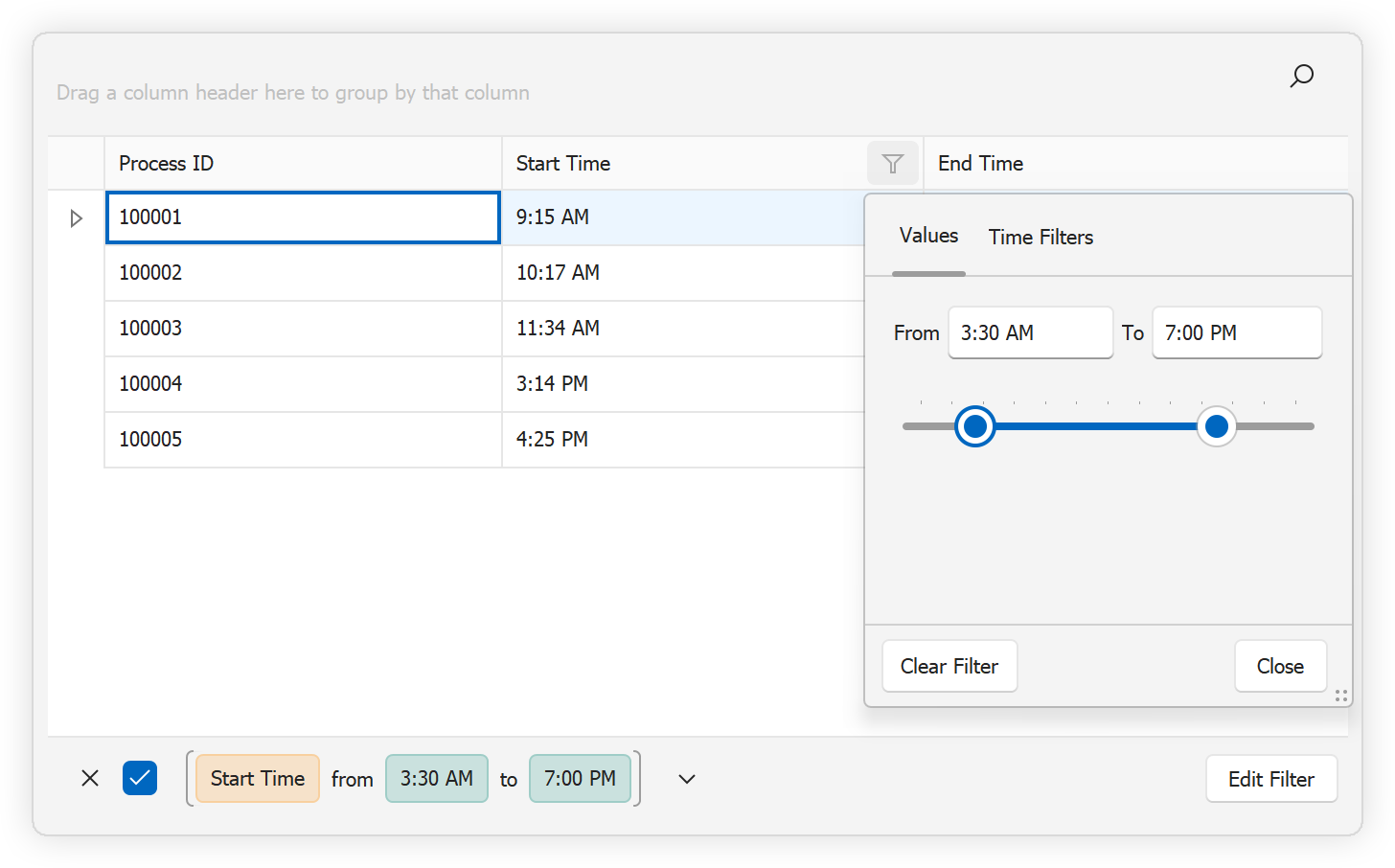
界面控件DevExpress WinForms v24.2新功能预览 - 支持.NET 9
DevExpress WinForms 拥有180组件和UI库,能为Windows Forms平台创建具有影响力的业务解决方案。DevExpress WinForms能完美构建流畅、美观且易于使用的应用程序,无论是Office风格的界面,还是分析处理大批量的业务数据,它都能轻松胜…...

Postman之pm.test断言操作
Postman之pm.test断言操作 1.断言方法2.连接符3.条件判断符 用于验证请求的响应数据是否符合预期 1.断言方法 pm.test():定义一个测试函数,接受两个参数,一个字符串参数用来描述该测试,一个返回True/False的函数 语法格式&#…...
对数几率回归
对数几率回归简介 对数几率回归(Logistic Regression)是一种用于解决分类问题的经典统计模型,其核心思想是利用逻辑函数(Sigmoid函数)将线性回归模型的输出值映射到概率范围 [0, 1],从而实现分类预测。对数…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
