SMO算法-核方法支持向量机

​ 我们现在的问题是要优化目标函数，同时求出参数向量$\alpha$
$$\begin{gathered} P=\underset{\alpha }{\underbrace{min}}\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0 \\ 0\le {\alpha }_i\le C \end{gathered}$$
​ 因为现在的问题是原来的对偶问题化简而来的所以$\alpha$还应该满足对偶互补条件${\alpha }_i(y_i(w^T{x}_i+b)-1+{\xi }_i^{\ast })=0$

​ 根据$\alpha$的取值范围和对偶互补条件我们可以分析出$\alpha$的情况：
$$\begin{gathered} {\alpha }_i=0\Rightarrow y_i(w\bullet \varphi (x_i)+b)\ge 1 \\ 0<{\alpha }_i<C\Rightarrow y_i(w\bullet \varphi (x_i)+b)=1 \\ {\alpha }_i=C\Rightarrow y_i(w\bullet \varphi (x_i)+b)\le 1 \end{gathered}$$
​ 为了方面表示我们做出一些字符替换：
$$\begin{gathered} g(x)=w\bullet \varphi (x)+b=\sum _{j=1}^m{\alpha }_j{y}_{j}K(x,x_j)+b \\ {K}_{ij}=\varphi (x_i)\bullet \varphi (x_j) \\ {E}_i=g(x_i)-y_i=\sum _{j=1}^m{\alpha }_j{y}_{j}K(x_i,x_j)+b-y_i \end{gathered}$$

2.3.2.1 思路

​ 我们的目标是求出m个${\alpha }_i$的值，如果同时去优化很难去得出结果，所以SMO选择和坐标下降算法类似的思路，选择两个参数先进行优化，将其他参数暂时看为常数，这样就能将问题简化为两变量的优化问题。我们假设除了${\alpha }_1,{\alpha }_2$外的都是常数我们可以得到约束条件：
$$\begin{gathered} {\alpha }_1{y}_1+{\alpha }_2{y}_2+\sum _{i=3}^m{\alpha }_i{y}_i=0 \\ {\alpha }_1{y}_1+{\alpha }_2{y}_2=-\sum _{i=3}^m{\alpha }_i{y}_i \\ Set\varsigma =-\sum _{i=3}^m{\alpha }_i{y}_i \\ \therefore {\alpha }_1{y}_1+{\alpha }_2{y}_2=\varsigma \end{gathered}$$
​ 同时我们从原问题P中将有${\alpha }_1,{\alpha }_2$的项提取出来：
$$\begin{gathered} P=\underset{\alpha }{\underbrace{min}}\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{K}_{ij}-\sum _{i=1}^m{\alpha }_i \\ =\underset{\alpha }{\underbrace{min}}\frac{1}{2}[{\alpha }_1^2{K}_{11}+{\alpha }_2^2{K}_{22}+2{\alpha }_1{\alpha }_2{y}_1{y}_2{K}_{12}+y_1{\alpha }_1\sum _{i=3}^m{y}_i{\alpha }_i{K}_{i1}+y_2{\alpha }_2\sum _{i=3}^m{y}_i{\alpha }_i{K}_{i2}]-{\alpha }_1-{\alpha }_2-\sum _{i=3}^m{\alpha }_i \\ =\underset{{\alpha }_1,{\alpha }_1}{\underbrace{min}}\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)+y_1{\alpha }_1\sum _{i=3}^m{y}_i{\alpha }_i{K}_{i1}+y_2{\alpha }_2\sum _{i=3}^m{y}_i{\alpha }_i{K}_{i2} \end{gathered}$$
​ 接下来我们就是要求解这个二元优化问题：

​ 首先我们要讨论${\alpha }_1,{\alpha }_2$的范围，${\alpha }_1和{\alpha }_2$是二元线性关系$ \alpha_1y_1+ \alpha_2y_2=\varsigma$，并且$\alpha$的取值范围为$0\le {\alpha }_i\le C$，同时y只取{+1和-1}，其实我们可以将线性关系分为四种情况去讨论：
$$\begin{gathered} IF:y_1==y_2 \\ {\alpha }_1+{\alpha }_2=kk>0ork<0 \\ IF:y_1!=y_2 \\ {\alpha }_1-{\alpha }_2=kk>0ork<0 \end{gathered}$$
​ 放到坐标系中如图所示：

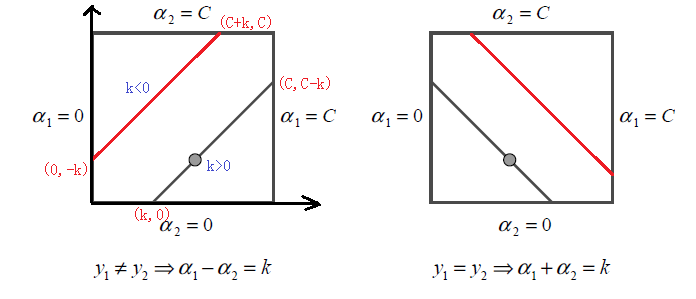
​ 由于${\alpha }_1,{\alpha }_2$的关系被限制在盒子里的一条线段上，所以两变量的优化问题实际上仅仅是一个变量的优化问题，我们可以直接视为是对变量${\alpha }_2$的优化。

​ 为了求出${\alpha }_2$的值，我们应该先求出${\alpha }_2$的定义域，我们假设${\alpha }_2$的左边界为L右边界为H。由于${\alpha }_1,{\alpha }_2$的取值其实是线上的动点问题，所以我们先研究${\alpha }_2^{new}$边界的取值。

​ 对于左图来说L和H的取值范围是：
$$L=max(0,{\alpha }_2^{old}-{\alpha }_1^{old})H=min(C,C+{\alpha }_2^{old}-{\alpha }_1^{old})$$
​ 推导：
∵ α 1 = α 2 + k 又 ∵ 0 ≤ α 1 ≤ C ∴ 0 ≤ α 2 + k ≤ C ∵ α 2 + k ≥ 0 且 α 2 ≥ 0 ∴ α 2 ≥ m a x { − k , 0 } = m a x { α 2 o l d − α 1 o l d , 0 } ∵ α 2 ≤ C − k 且 α 2 ≤ C ∴ α 2 ≤ m i n { C , C − K } ∴ L = m a x ( 0 , α 2 o l d − α 1 o l d ) H = m i n ( C , C + α 2 o l d − α 1 o l d ) \because \alpha_1 = \alpha_2 +k\\ 又\because 0\leq \alpha_1 \leq C \\\therefore 0\leq \alpha_2 +k \leq C \\ \because \alpha_2 +k \geq 0 且 \alpha_2 \geq 0 \\ \therefore \alpha_2 \geq max\{ -k,0\}=max\{ \alpha_2^{old} - \alpha_1^{old},0\} \\ \because \alpha_2 \leq C-k且 \alpha_2 \leq C \\ \therefore \alpha_2 \leq min\{C,C-K\} \\ \therefore L = max(0, \alpha_2^{old}-\alpha_1^{old}) \;\;\;H = min(C, C+\alpha_2^{old}-\alpha_1^{old}) ∵α1​=α2​+k又∵0≤α1​≤C∴0≤α2​+k≤C∵α2​+k≥0且α2​≥0∴α2​≥max{−k,0}=max{α2old​−α1old​,0}∵α2​≤C−k且α2​≤C∴α2​≤min{C,C−K}∴L=max(0,α2old​−α1old​)H=min(C,C+α2old​−α1old​)
​ 对于右图来说，推导同理：
$$L=max(0,{\alpha }_2^{old}+{\alpha }_1^{old}-C)H=min(C,{\alpha }_2^{old}+{\alpha }_1^{old})$$
​ 我们得到最终${\alpha }_2$的取值函数：
$${\alpha }_2^{new}=\{\begin{array}{ll}H& {\alpha }_2^{new,unc}>H\\ {\alpha }_2^{new,unc}& L\le {\alpha }_2^{new,unc}\le H\\ L& {\alpha }_2^{new,unc}<L\end{array}$$
​ 进一步我们优化函数为：
$$W({\alpha }_1,{\alpha }_2)=\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)+y_1{\alpha }_1{v}_1+y_2{\alpha }_2{v}_2$$
​ 代入${\alpha }_1=y_1(\varsigma -{\alpha }_2{y}_2)$，消去${\alpha }_1$

​ 最终我们得到纯${\alpha }_2$的函数：
$$W({\alpha }_2)=\frac{1}{2}{K}_{11}(\varsigma -{\alpha }_2{y}_2{)}^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_2{K}_{12}(\varsigma -{\alpha }_2{y}_2){\alpha }_2-(\varsigma -{\alpha }_2{y}_2)y_1-{\alpha }_2+(\varsigma -{\alpha }_2{y}_2)v_1+y_2{\alpha }_2{v}_2$$
​ 对${\alpha }_2$求导为0得到${\alpha }_2^{new,unc}$:
$${\alpha }_2^{new,unc}={\alpha }_2^{old}+\frac{y_2(E_1-E_2)}{K_{11}+K_{22}-2K_{12})}$$
​ 然后将${\alpha }_2^{new,unc}$代入取值函数则可得到最终的${\alpha }_2^{new}$，同时根据${\alpha }_1和{\alpha }_2$的线性关系:$${\alpha }_1{y}_1+{\alpha }_2{y}_2=\varsigma$$可以求出${\alpha }_1$

2.3.2.2 如何选择变量

一、第一个变量选择违反KKT条件最严重的点：

​ KKT条件为：
$$\begin{gathered} {\alpha }_i=0\Rightarrow y_{i}g(x_i)\ge 1 \\ 0<{\alpha }_i<C\Rightarrow y_{i}g(x_i)=1 \\ {\alpha }_i=C\Rightarrow y_{i}g(x_i)\le 1 \end{gathered}$$
​ 我们一般会选择违反$0<{\alpha }_i^{\ast }<C\Rightarrow y_{i}g(x_i)=1$这个条件的点，这是因为：对于${\alpha }_i=0$则意味着分类正确，这个点对于超平面的调整无效。对于${\alpha }_i=C$的点则代表点可能在错误间隔或者分类错误，对于这种情况其实无论怎么调整参数都无法优化超平面。

​ 对于违反$0 < \alpha_{i} < C $的点，此时意味着$\alpha_i >C \quad OR\quad \alpha_i <0$，我们很清楚$0\le {\alpha }_i\le C$，正常情况下不应该出现这种情况，进而说明KKT条件被违反，优化这些点能够更有效的让超平面向符合KKT条件的方向靠拢。

二、第二个变量选择$|E_1-E_2|$足够大的点：

​ $E_i=f(x_i)-y_i$代表预测值和真实值之间的误差，我们先选择好${\alpha }_1$计算出$E_1$，然后再在剩下的点中算出所有的$E_i$，对比这些$E_1-E_i$，较大的误差差说明模型在这两个点附近的差异更大，调整$\alpha$ 可以让模型更有效的向正确的分类移动，进而加速收敛速度

​ $E_1-E_i$ 较大时，可以使得分类超平面向调整幅度大的方向走。

三、更新$E_i$和b
$$\begin{gathered} \because y_1-\sum _{i=1}^m{\alpha }_i{y}_i{K}_{i1}-b_1=0 \\ \therefore b_1^{new}=y_1-\sum _{i=3}^m{\alpha }_i{y}_i{K}_{i1}-{\alpha }_1^{new}{y}_1{K}_{11}-{\alpha }_2^{new}{y}_2{K}_{21} \\ \therefore E_1=g(x_1)-y_1=\sum _{i=3}^m{\alpha }_i{y}_i{K}_{i1}+{\alpha }_1^{old}{y}_1{K}_{11}+{\alpha }_2^{old}{y}_2{K}_{21}+b^{old}-y_1 \\ 联立两式 \\ {b}_1^{new}=-E_1-y_1{K}_{11}({\alpha }_1^{new}-{\alpha }_1^{old})-y_2{K}_{21}({\alpha }_2^{new}-{\alpha }_2^{old})+b^{old} \\ 同理: \\ {b}_2^{new}=-E_2-y_1{K}_{12}({\alpha }_1^{new}-{\alpha }_1^{old})-y_2{K}_{22}({\alpha }_2^{new}-{\alpha }_2^{old})+b^{old} \\ \therefore b^{new}=\frac{b_1^{new}+b_2^{new}}{2} \\ 更新:E_i=\sum _S{y}_j{\alpha }_{j}K(x_i,x_j)+b^{new}-y_i \end{gathered}$$

2.3.2.2 算法

​ 输入是m个样本( $ x_ {1} $ , $ y_ {1} $ ),( $ x_ {2} $ , $ y_ {2} $ ), $ \cdots $ ,( $ x_ {m} $ , $ y_ {m} $ ),其中x为n维特征向量。y为二元输出,值为1,或者-1

​ 输出是近似解 $ \alpha $

1. 取初值 $ \alpha ^ {0} $ =0,k=0

2. 选出${\alpha }_1和{\alpha }_2$

3. 求出${\alpha }_2^{new,unc}$ $={\alpha }_2^{old}$ + $\frac{y_2(E_1-E_2)}{K_{11}+K_{22}-2K_{12}}$

4. 求出${\alpha }_2^{new}=\{\begin{array}{ll}H& {\alpha }_2^{new,unc}>H\\ {\alpha }_2^{new,unc}& L\le {\alpha }_2^{new,unc}\le H\\ L& {\alpha }_2^{new,unc}<L\end{array}$

5. 利用 ${\alpha }_2^{new}$ 和 ${\alpha }_1^{new}$ 的关系求出 ${\alpha }_1^{new}$

6. 计算 $b^{k+1}$ 和 $E_i$

7. 检查是否满足如下的终止条件KKT:
   $$\begin{gathered} \sum _{i=1}^m{\alpha }_i{y}_i=0 \\ 0\le {\alpha }_i\le C,i=1,\mathrm{2...}m \\ {\alpha }_i=0\Rightarrow y_{i}g(x_i)\ge 1 \\ 0<{\alpha }_i<C\Rightarrow y_{i}g(x_i)=1 \end{gathered}$$

8. 如果满足则结束,返回 $\alpha$ ,否则转到步骤2)。