数据结构在二叉树Oj中利用子问题思路来解决问题
二叉树Oj题
- 获取二叉树的节点数
- 获取二叉树的终端节点个数
- 获取k层节点的个数
- 获取二叉树的高度
- 检测为value的元素是否存在
- 判断两颗树是否相同
- 判断是否是另一棵的子树
- 反转二叉树
- 判断一颗二叉树是否是平衡二叉树
- 时间复杂度O(n*n)
- 复杂度O(N)
- 二叉树的遍历
- 判断是否是对称的二叉树
- 二叉树的层序遍历
获取二叉树的节点数
首先从左树开始递到最下一层,当最后一层H没有节点时,归回+1以此类推,最终返回的节点就是我们树的节点树。

public int getNodeCount(TreeNode root){if(root==null)return 0;return getNodeCount(root.left)+getNodeCount(root.right)+1;}
获取二叉树的终端节点个数
首先清楚二叉树的终端结点是什么?
终端结点说明它的度为0(没有子树),所以左树和右树的值为null,而我们就只需要判断一下,如果左树和右树值为null,则就是一个叶子结点+1.

public int getLeafCount(TreeNode root){if(root==null)return 0;if(root.left==null&&root.right==null){return 1;}return getLeafCount(root.left)+getLeafCount(root.right);}
获取k层节点的个数
第一层为我们的根节点,它的个数一定是1,而根的左树和右树则为2,以此类推

首先我们的第一个条件是k为1时一定会有一个节点数
这里当我们递出去时,我们就会减少一层当k等于1时,这里我们就在k层找到一个节点然后回归到父节点然后继续子树找下一个节点,知道将k层的节点数遍历完。

public int getLevelCount(TreeNode root,int k){if(root==null)return 0;if(k==1)return 1;return getLevelCount(root.left,k-1)+getLevelCount(root.right,k-1);}
获取二叉树的高度
这里直接求左子树的最大高度和右子树的最大高度然后进行比较,然后返回最大的高度值就可以


public int getBinaryTreeHeight(TreeNode root){if(root==null)return 0;int maxtLeftHeight=getBinaryTreeHeight(root.left);int maxRightHeight=getBinaryTreeHeight(root.right);return maxLeftHeight>maxRightHeight?maxLeftHeight+1:maxRightHeight+1;}
检测为value的元素是否存在
首先root根和递归的条件不能为空
然后判断root的值是否为value值并返回这个值
用一个ret来接收其返回值,然后判断ret不为空,则回来的值将root的value值带回
(ret如果为空,说明root根或者递归的条件就是空的,没有要找的元素)

public TreeNode find(TreeNode root,String val){if(root==null)return null;if(root.val.equals(val)) return root;TreeNode ret1 = find(root.left,val);if(ret1!=null)return ret1;TreeNode ret2 = find(root.right,val);if(ret2!=null)return ret2;return null;}
判断两颗树是否相同
判断两颗树是否相同
首先根节点到叶子结点两者的结构相同
然后是根节点到叶子结点的值要相同
如果说一棵树为空但是另一个树不为空,说明两棵树的结构一定是不同的
如果两颗树都为空,加上上述说明两棵树的结构一致
接下来判断节点的值
两颗树的节点值如果不一样,则也不是相同的
最后判断两颗树左树和右树是否一致

public boolean isSameTree(TreeNode tree1,TreeNode tree2){//两棵树如果同时走一个有节点一个没有节点一定不相同if(tree1==null&&tree2!=null||tree1!=null&&tree2==null)return false;//两棵树都为null说明都没有可以走的节点if(tree1==null&&tree2==null)return true;//判断结构//判断节点值是否相同不同为falseif(!tree1.val.equals(tree2.val)return false;return isSameTree(tree1.left,tree2.left)&&isSameTree(tree1.right,tree2.right);}
判断是否是另一棵的子树
判断是否是tree中的一颗子树,subtree一定是t在ree中头节点左子树中或者是右子树中,如果不在这里直接返回false
这里由tree的左子树和右子树递归找到subtree的根节点,找到后将tree中的subtree子树与subtree同时遍历来确认是否为一个相同的树。

public boolean isSubtree(TreeNode root, TreeNode subRoot) {//是相同的树节点返回trueif(isSameTree(root,subRoot))return true;//递归如果出现root为null时,因为没有语句拦截,root会继续往下走导致空指针异常//subRoot为null直接返回false,主树不在进行下面的递归if(root==null||subRoot==null)return false;if(isSubtree(root.left,subRoot))return true;if(isSubtree(root.right,subRoot))return true;return false;}
反转二叉树
将二叉树的每个节点的左子树和右子树互换


public TreeNode invertTree(TreeNode root) {if(root==null)return null;TreeNode tmp=root.left;root.left=root.right;root.right=tmp;invertTree(root.left);invertTree(root.right);return root;}
判断一颗二叉树是否是平衡二叉树
时间复杂度O(n*n)
该题判断二叉树是否是平衡二叉树的条件是:左子树与右子树的绝对值一定小于或者等于1,如果高度大于1则非平衡二叉树。
如果根节点只有一个节点或者他的左右子树差的绝对值为0,则为平衡二叉树

只判断了根的节点的话它的左右子树的差确实为1,但是左子树中b的左子树和右子树的差值为2,这也不是一个平衡的二叉树。

public boolean isBalanced(TreeNode root) {if(root==null)return true;//root为null直接返回为空int leftHeight = maxDepth(root.left);//求左树的高度int rightHeight = maxDepth(root.right);//求右树的高度return Math.abs(leftHeight-rightHeight)<=1//判断&&isBalanced(root.left)&&isBalanced(root.right);}public int maxDepth(TreeNode root){//求二叉树的最大深度if(root==null)return 0;int leftHeight=maxDepth(root.left);int rightHeight=maxDepth(root.right);return leftHeight>rightHeight?leftHeight+1:rightHeight+1;}
复杂度O(N)

这里如果我们在找左右子树高度的差值时如果发现了它差值大于1的情况,我们直接返回-1,当最后回归到根节点左右子树时,差值也大于1
class Solution {public boolean isBalanced(TreeNode root) {if(root==null)return true;int ret =maxDepth(root);//接收ret为-1则左右子树差值一定大于1if(ret==-1){return false;}return true;}public int maxDepth(TreeNode root){//求二叉树的最大深度if(root==null)return 0;int leftHeight=maxDepth(root.left);int rightHeight=maxDepth(root.right);//走到这里最靠下的边上的左右子树求得高度if(leftHeight>=0&&rightHeight>=0&&Math.abs(leftHeight-rightHeight)<=1){//说明左右子树的绝对值为<=1并且大于等于0//返回左右子树中最大的一个高度+1return Math.max(leftHeight,rightHeight)+1;}else{return -1;}}
}
二叉树的遍历

首先创建一个类来实现构造二叉树的前提
因为题目条件给定的是输入一串字符串然后先序遍历这个字符串来建立起二叉树,然后通过中序遍历在进行打印

class TreeNode {public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}
}
public class Main {public static int i = 0;public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextLine()) {String str=in.nextLine();TreeNode root=createTree(str);inOrder(root);}}public static TreeNode createTree(String str) {TreeNode root=null;//遍历字符串str来获取字符来给到root,因为不确定root是不是空节点。if (str.charAt(i) != '#') {root =new TreeNode(str.charAt(i));i++;//通过i++来递归左右树root.left=createTree(str);root.right=createTree(str);} else {//跳过#i++;}return root;}//中序遍历public static void inOrder(TreeNode root) {if (root == null)return ;inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}
判断是否是对称的二叉树
二叉树反转过来的镜像就是对称的二叉树
这里直接从根节点的左树和右树下手
满足条件1:二叉树的结构相同
满足条件2:二叉树的对称值相同
左子树中的左树对应右子树的右树
右子树的左树对应左子树的右树

public boolean isSymmetric(TreeNode root) {if(root==null)return true;//判断左右节点是否对称return isSymmetricChild(root.left,root.right);}public boolean isSymmetricChild(TreeNode t1,TreeNode t2){//这里t1和t2的结构不相同if(t1==null&&t2!=null||t1!=null&&t2==null)return false;//两者都为空,说明结构相同走向空节点if(t1==null&&t2==null)return true;//到这里结构相同检查对称值if(t1.val!=t2.val)return false;//满足左右子树的对称条件 return isSymmetricChild(t1.left,t2.right)&&isSymmetricChild(t1.right,t2.left);}
二叉树的层序遍历
二叉树层序遍历是地1层开始从左到右,从上到下开始遍历。
如果用二维数组来进行层序遍历怎么做呢?
这里需要用到队列,因为第一层的根节点永远是1,我们将它放入到队列中来遍历这个队列
如果a释放完且a树的值给到了一维数组后,会得到b和c两个子树并放到队列中,这时候需要一个计数器来计算当前的层数,当层数为0时,我们将一维数组所有的值放到二维数组中就好了

public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> line=new ArrayList<List<Integer>>();if(root==null)return line;Queue<TreeNode> queue=new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){int size=queue.size();List<Integer> col=new ArrayList<Integer>();while(size!=0){TreeNode cur = queue.poll();col.add(cur.val);size--;if(cur.left!=null) queue.offer(cur.left);if(cur.right!=null) queue.offer(cur.right);}line.add(col);}return line;}
相关文章:

数据结构在二叉树Oj中利用子问题思路来解决问题
二叉树Oj题 获取二叉树的节点数获取二叉树的终端节点个数获取k层节点的个数获取二叉树的高度检测为value的元素是否存在判断两颗树是否相同判断是否是另一棵的子树反转二叉树判断一颗二叉树是否是平衡二叉树时间复杂度O(n*n)复杂度O(N) 二叉树的遍历判断是否是对称的二叉树二叉…...

华为openEuler考试真题演练(附答案)
【单选题】 以下关于互联网的描述,哪个选项是正确的? A:Nginx 在万维网中可以作为 ftp 服务器的反向代理,并与ftp服务器的数量--对应 B:Nginx 在互联网中可以作为 web服务器端,成为万维网的一个节点 C:互联网上的的资源需使用 Nginx进行七层…...

生成自签名证书并配置 HTTPS 使用自签名证书
生成自签名证书 1. 运行 OpenSSL 命令生成证书和私钥 在终端中输入以下命令,生成自签名证书和私钥文件: sudo openssl req -x509 -nodes -days 365 -newkey rsa:2048 -keyout self_signed.key -out self_signed.pem-x509:生成自签名证书。…...

物联网核心安全系列——智能汽车安全防护的重要性
汽车行业引入的智能硬件技术已经越来越多,早先设计者更多考虑到的是硬件成本和软件用户体验等因素,但随着国外两位技术人员成功实现远程控制汽车的视频曝出后,智能汽车安全便成为了一个热议话题。 汽车总线架构及原理比较复杂,日…...

数据库视图
数据库视图(Database View)是数据库中的虚拟表,其内容由查询定义,通常用来简化复杂的查询或提供安全访问数据。视图并不存储实际数据,而是将查询的结果集作为一个“虚拟表”呈现。用户通过查询视图,就可以看…...
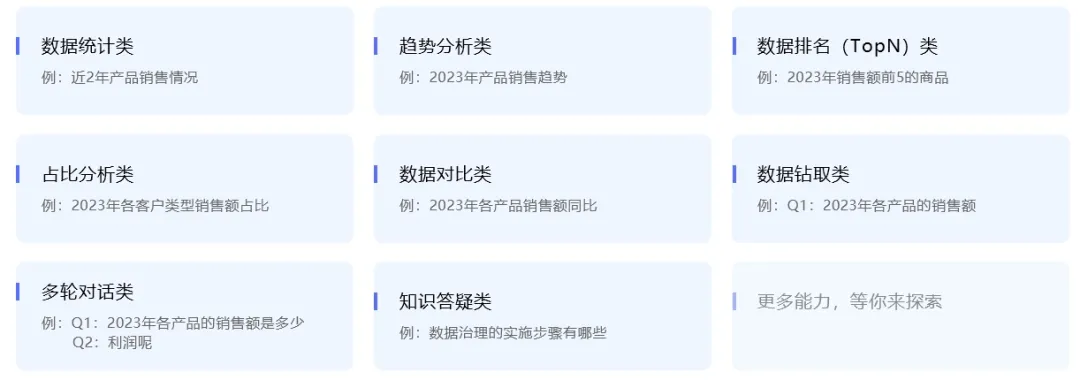
从传统分析到智能问数,打造零门槛数据分析方案
众所周知,传统报表和自助分析工具存在使用门槛,且早期智能分析不够智能。随着AI技术发展,现有数据应用模式难以满足多样化、快速变化的需求,数据驱动、敏捷决策、精细运营成为了各大企业的新课题。 01企业数据应用挑战 业务人员的…...

java 设计模式 模板方法模式
模板方法模式(Template Method Pattern)是一种行为型设计模式,它在父类中定义一个算法的框架,允许子类在不改变算法结构的情况下重写算法的某些特定步骤。这种模式非常适合于那些有一定公共流程,但某些步骤需要子类定制…...

基于UDP和TCP实现回显服务器
目录 一. UDP 回显服务器 1. UDP Echo Server 2. UDP Echo Client 二. TCP 回显服务器 1. TCP Echo Server 2. TCP Echo Client 回显服务器 (Echo Server) 就是客户端发送什么样的请求, 服务器就返回什么样的响应, 没有任何的计算和处理逻辑. 一. UDP 回显服务器 1. UD…...

在 CentOS 系统上直接安装 MongoDB 4.0.25
文章目录 步骤 1:配置 MongoDB 官方源步骤 2:安装 MongoDB步骤 3:启动 MongoDB 服务步骤 4:验证安装步骤 5:可选配置注意事项 以下是在 CentOS 系统上直接安装 MongoDB 4.0.25 的详细步骤: 步骤 1&#x…...

Android和IOS的区别
一、系统区别 1、系统和框架的区别 (1)Android系统的底层建立在Linux系统之上;而ios基于UNIX系统 Android完全开放,iOS完全封源开发 (2)编程语言:Android的编程语言是Java和KotLin;而ios的则为O…...

数据库基础(MySQL)
1. 数据库基础 1.1 什么是数据库 存储数据用文件就可以了,为什么还要弄个数据库? 文件保存数据有以下几个缺点: 文件的安全性问题文件不利于数据查询和管理文件不利于存储海量数据文件在程序中控制不方便 数据库存储介质: 磁盘内存 为…...

Vue前端开发子组件向父组件传参
在父组件中,如果需要获取子组件中的数据,有两种方式,一种是在子组件中自定义事件,父组件绑定该事件,当触发自定义事件时,向父组件传入参数;另一种是先通过ref属性给子组件命名,然后在父组件中就…...

javaScript语法基础(函数,对象,常用类Array,String,Math和Date)
# 本文详细结束了JavaScript中函数、对象、常用类Array,String,Math和Date的用法。 一、函数 1、概述 将程序中多次要用到的代码块封装起来,就是函数。函数使代码块的重复使用更方便,且功能独立,便于维护。 2、函数的…...

WebStorm 2022.3.2/IntelliJ IDEA 2024.3出现elementUI提示未知 HTML 标记、组件引用爆红等问题处理
WebStorm 2022.3.2/IntelliJ IDEA 2024.3出现elementUI提示未知 HTML 标记、组件引用爆红等问题处理 1. 标题识别elementUI组件爆红 这个原因是: 在官网说明里,才版本2024.1开始,默认启用的 Vue Language Server,但是在 Vue 2 项…...

k8s-NetworkPolicy
NetworkPolicy 是k8s中的网络策略可以限制pod以及namespace之间的访问流量 演示一下名称空间之间基于端口的访问限制 官方对networkpolicy的介绍 官方网址: 网络策略 |Kubernetes (简体中文) 一:创建NetworkPolicy vim…...

【C++】踏上C++学习之旅(九):深入“类和对象“世界,掌握编程的黄金法则(四)(包含四大默认成员函数的练习以及const对象)
文章目录 前言1. 实现Date类的构造函数2. 实现Date类的拷贝构造函数3. 实现Date类的赋值运算符重载4. 实现各Date对象之间的比较接口5. 实现Date对象的加减接口6. const成员7. 取地址及const取地址操作符重载 前言 在我们前面学习到了"类和对象"的四大默认成员函数(…...

C++——智能指针剖析
参考: 恋恋风辰官方博客 动态内存管理 - cppreference.com SRombauts/shared_ptr: 一个最小的 shared/unique_ptr 实现,用于处理 boost/std::shared/unique_ptr 不可用的情况。 C智能指针_c 智能指针-CSDN博客 当…...
241119.LeetCode——383.赎金信
题目描述 给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true ;否则返回 false 。 magazine 中的每个字符只能在 ransomNote 中使用一次。 示例 1: 输…...

基于SSM的农家乐管理系统+论文示例参考
1.项目介绍 功能模块:管理员(农家乐管理、美食信息管理、住宿信息管理、活动信息、用户管理、活动报名、论坛等),普通用户(注册登录、活动报名、客房预订、用户评价、收藏管理、模拟支付等)技术选型&#…...

用 Python 从零开始创建神经网络(九):反向传播(Backpropagation)(还在更新中。。。)
反向传播(Backpropagation) 引言1. 分类交叉熵损失导数(Categorical Cross-Entropy loss derivative)2. 分类交叉熵损失衍生代码实现3. Softmax激活导数(Softmax activation derivative)4. Softmax激活函数…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
