当前位置： 首页 > news >正文

P11290 【MX-S6-T2】「KDOI-11」飞船

news 2025/7/15 5:28:53

题目大意：有i种加油站，最开始速度为1，每次加油可以使速度*v，每次加油有一个时间代价，求到达终点所需最小时间。

思路：不妨考虑dp，贪心是错误的。

对于速度而言，y<=10^9，所以速度一定<10^9，所以速度是指数增长的，状态数不会很多。

于是只有两种状态2^j*3^k，设f[i][j][k]表示前i个加油站加到速度为2^j*3^k。

有两种转移策略：

1.f[i][j][k]=min(f[i-1][j][k]+(a[i].x-a[i-1].x)/1.0/(fac1[j]*fac2[k]),f[i][j][k]);

表示继承前一个点的值

2.f[i][j][k]=min(f[i-1][j-1][k]+a[i].t*1.0+(a[i].x-a[i-1].x)/1.0/(fac1[j-1]*fac2[k]),f[i][j][k]);

当且仅当vi=2

3.f[i][j][k]=min(f[i-1][j][k-1]+a[i].t*1.0+(a[i].x-a[i-1].x)/1.0/(fac1[j]*fac2[k-1]),f[i][j][k]);

当且仅当vi=3

4.vi=4同理

考虑计算答案，对于每一个终点而言，离它最近且不在它的位置上是最优的。因为这个点记录了前i个点的最优值

枚举每种状态即可，复杂度O(n*log_{2}^2(\alpha ))级别

相关文章：

P11290 【MX-S6-T2】「KDOI-11」飞船

题目大意&#xff1a;有i种加油站&#xff0c;最开始速度为1&#xff0c;每次加油可以使速度*v&#xff0c;每次加油有一个时间代价&#xff0c;求到达终点所需最小时间。 思路&#xff1a;不妨考虑dp&#xff0c;贪心是错误的。 对于速度而言&#xff0c;&#xff0c;所以速…...

编程日记 2024/11/22 7:02:14

WebGIS地图框架有哪些?

地理信息系统&#xff08;GIS&#xff09;已经成为现代应用开发中不可或缺的一部分&#xff0c;尤其在前端开发中。随着Web技术的快速发展&#xff0c;许多强大而灵活的GIS框架涌现出来&#xff0c;为开发人员提供了丰富的工具和功能&#xff0c;使他们能够创建交互式、高性能的…...

编程日记 2024/11/22 6:59:11

量化加速知识点（整理中。。。）

量化的基本概念 通过减少模型中计算精度&#xff0c;从而减少模型计算所需要的访存量。 参考...

编程日记 2024/11/22 6:55:07

BLIP-2模型的详解与思考

大模型学习笔记------BLIP-2模型的详解与思考 1、BLIP-2框架概述2、BLIP-2网络结构详解3、BLIP-2的几点思考 上一篇文章上文中讲解了 BLIP&#xff08;Bootstrapping Language-Image Pretraining&#xff09;模型的一些思考&#xff0c;本文将讲述一个BLIP的升级版 BLIP-2&am…...

编程日记 2024/11/22 6:54:05

2024年11月22日 十二生肖 今日运势

小运播报&#xff1a;2024年11月22日&#xff0c;星期五&#xff0c;农历十月廿二 &#xff08;甲辰年乙亥月庚寅日&#xff09;&#xff0c;法定工作日。 红榜生肖&#xff1a;马、猪、狗 需要注意&#xff1a;牛、蛇、猴 喜神方位&#xff1a;西北方 财神方位&#xff1a…...

编程日记 2024/11/22 6:50:02

小米C++ 面试题及参考答案上（120道面试题覆盖各种类型八股文）

进程和线程的联系和区别 进程是资源分配的基本单位&#xff0c;它拥有自己独立的地址空间、代码段、数据段和堆栈等。线程是进程中的一个执行单元&#xff0c;是 CPU 调度的基本单位。 联系方面&#xff0c;线程是进程的一部分&#xff0c;一个进程可以包含多个线程。它们都用于…...

编程日记 2024/11/22 6:46:59

SQL SELECT 语句：基础与进阶应用

SQL SELECT 语句&#xff1a;基础与进阶应用 SQL&#xff08;Structured Query Language&#xff09;是一种用于管理关系数据库的编程语言。在SQL中&#xff0c;SELECT语句是最常用的命令之一&#xff0c;用于从数据库表中检索数据。本文将详细介绍SELECT语句的基础用法&#…...

编程日记 2024/11/22 6:45:58

微服务即时通讯系统的实现（服务端）----（1）

目录 1. 项目介绍和服务器功能设计2. 基础工具安装3. gflags的安装与使用3.1 gflags的介绍3.2 gflags的安装3.3 gflags的认识3.4 gflags的使用 4. gtest的安装与使用4.1 gtest的介绍4.2 gtest的安装4.3 gtest的使用 5 Spdlog日志组件的安装与使用5.1 Spdlog的介绍5.2 Spdlog的安…...

编程日记 2024/11/22 6:44:57

《Spring 依赖注入方式全解析》

一、Spring 依赖注入概述 Spring 依赖注入&#xff08;Dependency Injection&#xff0c;DI&#xff09;是一种重要的设计模式&#xff0c;它在 Spring 框架中扮演着关键角色。依赖注入的核心概念是将对象所需的依赖关系由外部容器&#xff08;通常是 Spring 容器&#xff09;进…...

编程日记 2024/11/22 6:43:54

【C++动态规划】1411. 给 N x 3 网格图涂色的方案数|1844

本文涉及知识点 C动态规划 LeetCode1411. 给 N x 3 网格图涂色的方案数 提示 你有一个 n x 3 的网格图 grid &#xff0c;你需要用 红&#xff0c;黄&#xff0c;绿 三种颜色之一给每一个格子上色&#xff0c;且确保相邻格子颜色不同&#xff08;也就是有相同水平边或者垂直…...

编程日记 2024/11/22 6:41:51

外包干了3年，技术退步明显...

先说情况&#xff0c;大专毕业&#xff0c;18年通过校招进入湖南某软件公司&#xff0c;干了接近6年的功能测试&#xff0c;今年年初&#xff0c;感觉自己不能够在这样下去了&#xff0c;长时间呆在一个舒适的环境会让一个人堕落&#xff01; 而我已经在一个企业干了四年的功能…...

编程日记 2024/11/22 6:40:51

SpringBoot 2.x 整合 Redis

整合 1&#xff09;添加依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency> <!-- 如果没有使用下面给出的工具类&#xff0c;那么就不需要引入 -…...

编程日记 2024/11/22 6:39:49

React的API✅

createContext createContext要和useContext配合使用&#xff0c;可以理解为 “React自带的redux或mobx” &#xff0c;事实上redux就是用context来实现的。但是一番操作下来我还是感觉&#xff0c;简单的context对视图的更新的细粒度把控比不上mobx&#xff0c;除非配合memo等…...

编程日记 2024/11/22 6:38:47

什么是全渠道客服中心？都包括哪些电商平台？

什么是全渠道客服中心&#xff1f;都包括哪些电商平台&#xff1f; 作者&#xff1a;开源呼叫中心系统 FreeIPCC&#xff0c;Github地址&#xff1a;https://github.com/lihaiya/freeipcc 全渠道客服中心是一种能够同时接入并处理来自多个渠道客户咨询和请求的综合服务平台。以…...

编程日记 2024/11/22 6:37:45

Jtti：如何知晓服务器的压力上限?具体的步骤和方法

了解服务器的压力上限(也称为性能极限或容量)是确保系统在高负载下仍能稳定运行的重要步骤。这通常通过压力测试(也称为负载测试或性能测试)来实现。以下是详细的步骤和方法来确定服务器的压力上限&#xff1a; 1. 定义测试目标和指标 在进行压力测试前&#xff0c;明确测试目标…...

编程日记 2024/11/22 6:36:44

贪心算法（1）

目录 柠檬水找零 题解&#xff1a; 代码&#xff1a; 将数组和减半的最少操作次数&#xff08;大根堆&#xff09; 题解&#xff1a; 代码&#xff1a; 最大数&#xff08;注意 sort 中 cmp 的写法&#xff09; 题解&#xff1a; 代码&#xff1a; 摆动序列&#xff0…...

编程日记 2024/11/22 6:35:42

SpringBoot，IOC，DI，分层解耦，统一响应

目录 详细参考day05 web请求 1、BS架构流程 2、RequestParam注解 完成参数名和形参的映射 3、controller接收json对象&#xff0c;使用RequestBody注解 4、PathVariable注解传递路径参数 5、ResponseBody&#xff08;return 响应数据&#xff09; RestController源码 6、统一响…...

编程日记 2024/11/22 6:34:42

目标驱动学习python动力

文章目录 迟迟未开始的原因打破思维里的围墙抛砖引玉爬虫 结束词 迟迟未开始的原因 其实我也是很早就知道有python&#xff0c;当时听说这个用于做测试不错&#xff0c;也就一直没有提起兴趣&#xff0c;后来人工智能火了之后&#xff0c;再次接触python&#xff0c;安装好pyth…...

编程日记 2024/11/22 6:32:40

力扣-Hot100-回溯【算法学习day.39】

前言 ###我做这类文档一个重要的目的还是给正在学习的大家提供方向&#xff08;例如想要掌握基础用法&#xff0c;该刷哪些题&#xff1f;&#xff09;我的解析也不会做的非常详细&#xff0c;只会提供思路和一些关键点&#xff0c;力扣上的大佬们的题解质量是非常非常高滴&am…...

编程日记 2024/11/22 6:31:39

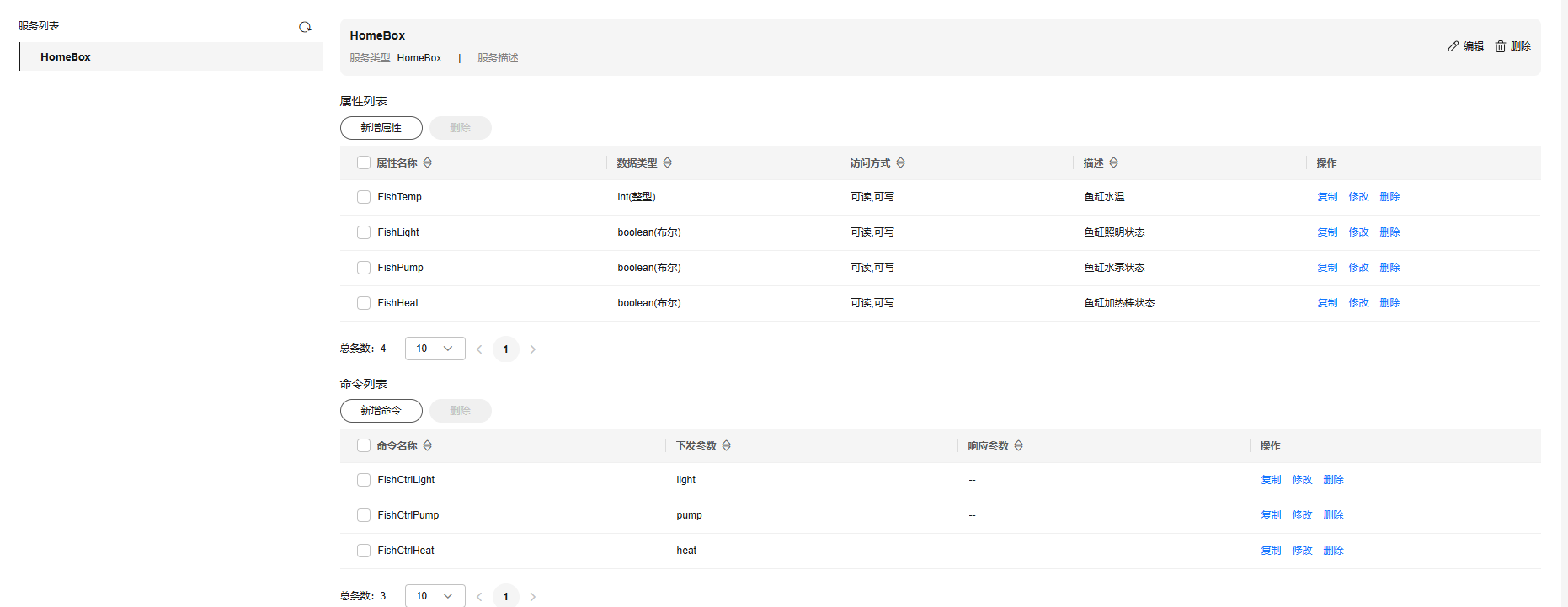
小熊派Nano接入华为云

一、华为云IoTDA创建产品 创建如下服务&#xff0c;并添加对应的属性和命令。 二、小熊派接入 根据小熊派官方示例代码D6完成了小熊派接入华为云并实现属性上传命令下发。源码&#xff1a;小熊派开源社区/BearPi-HM_Nano 1. MQTT连接代码分析 这部分代码在oc_mqtt.c和oc_mq…...

编程日记 2024/11/22 6:29:36

React hook之useRef

React useRef 详解 useRef 是 React 提供的一个 Hook&#xff0c;用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途&#xff0c;下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

编程新知 2025/6/11 15:21:26

相机Camera日志实例分析之二：相机Camx【专业模式开启直方图拍照】单帧流程日志详解

【关注我&#xff0c;后续持续新增专题博文&#xff0c;谢谢&#xff01;&#xff01;&#xff01;】 上一篇我们讲了&#xff1a; 这一篇我们开始讲&#xff1a; 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下&#xff1a; 一、场景操作步骤 操作步…...

编程新知 2025/7/10 22:40:01

令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍

文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结&#xff1a; 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析&#xff1a; 实际业务去理解体会统一注…...

编程新知 2025/7/14 23:09:38

深度学习习题2

1.如果增加神经网络的宽度&#xff0c;精确度会增加到一个特定阈值后&#xff0c;便开始降低。造成这一现象的可能原因是什么&#xff1f; A、即使增加卷积核的数量&#xff0c;只有少部分的核会被用作预测 B、当卷积核数量增加时&#xff0c;神经网络的预测能力会降低 C、当卷…...

编程新知 2025/7/13 18:18:34

面向无人机海岸带生态系统监测的语义分割基准数据集

描述&#xff1a;海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而&#xff0c;目前该领域仍面临一个挑战&#xff0c;即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

编程新知 2025/7/13 12:53:56

Linux 中如何提取压缩文件 ？

Linux 是一种流行的开源操作系统&#xff0c;它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间&#xff0c;使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的&#xff0c;要在 …...

编程新知 2025/7/14 13:30:43

基于Springboot+Vue的办公管理系统

角色&#xff1a; 管理员、员工 技术&#xff1a; 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能&#xff1a; 该办公管理系统是一个综合性的企业内部管理平台&#xff0c;旨在提升企业运营效率和员工管理水…...

编程新知 2025/7/14 2:40:52

LRU 缓存机制详解与实现（Java版） + 力扣解决

&#x1f4cc; LRU 缓存机制详解与实现&#xff08;Java版&#xff09; 一、&#x1f4d6; 问题背景 在日常开发中&#xff0c;我们经常会使用 缓存&#xff08;Cache&#xff09; 来提升性能。但由于内存有限&#xff0c;缓存不可能无限增长&#xff0c;于是需要策略决定&am…...

编程新知 2025/7/8 17:57:05

【MATLAB代码】基于最大相关熵准则（MCC）的三维鲁棒卡尔曼滤波算法（MCC-KF），附源代码|订阅专栏后可直接查看

文章所述的代码实现了基于最大相关熵准则（MCC）的三维鲁棒卡尔曼滤波算法（MCC-KF），针对传感器观测数据中存在的脉冲型异常噪声问题，通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现，验证了后者在状态估计鲁棒性方面的显著优…...

编程新知 2025/7/11 1:16:30

机器学习的数学基础：线性模型

线性模型 线性模型的基本形式为&#xff1a; f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法&#xff0c;得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

编程新知 2025/7/11 14:37:06