二分查找题目:有序数组中的单一元素
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:有序数组中的单一元素
出处:540. 有序数组中的单一元素
难度
4 级
题目描述
要求
给定一个仅由整数组成的升序数组,其中每个元素都出现两次,除了一个元素只出现一次。
返回只出现一次的元素。
要求时间复杂度是 O(log n) \texttt{O(log n)} O(log n),空间复杂度是 O(1) \texttt{O(1)} O(1)。
示例
示例 1:
输入: nums = [1,1,2,3,3,4,4,8,8] \texttt{nums = [1,1,2,3,3,4,4,8,8]} nums = [1,1,2,3,3,4,4,8,8]
输出: 2 \texttt{2} 2
示例 2:
输入: nums = [3,3,7,7,10,11,11] \texttt{nums = [3,3,7,7,10,11,11]} nums = [3,3,7,7,10,11,11]
输出: 10 \texttt{10} 10
数据范围
- 1 ≤ nums.length ≤ 10 5 \texttt{1} \le \texttt{nums.length} \le \texttt{10}^\texttt{5} 1≤nums.length≤105
- 0 ≤ nums[i] ≤ 10 5 \texttt{0} \le \texttt{nums[i]} \le \texttt{10}^\texttt{5} 0≤nums[i]≤105
解法一
思路和算法
由于给定的数组已经排序,因此相同元素在数组中一定位于相邻的位置。对于只出现一次的元素,该元素的左边和右边各有偶数个元素。假设只出现一次的元素位于下标 index \textit{index} index,考虑下标 x x x 处的元素, x ≠ index x \ne \textit{index} x=index。
-
当 x < index x < \textit{index} x<index 时,只出现一次的元素在下标 x x x 的右边。如果 x x x 是偶数,则 nums [ x ] = nums [ x + 1 ] \textit{nums}[x] = \textit{nums}[x + 1] nums[x]=nums[x+1];如果 x x x 是奇数,则 nums [ x ] = nums [ x − 1 ] \textit{nums}[x] = \textit{nums}[x - 1] nums[x]=nums[x−1]。
-
当 x > index x > \textit{index} x>index 时,只出现一次的元素在下标 x x x 的左边。如果 x x x 是偶数,则 nums [ x ] = nums [ x − 1 ] \textit{nums}[x] = \textit{nums}[x - 1] nums[x]=nums[x−1];如果 x x x 是奇数,则 nums [ x ] = nums [ x + 1 ] \textit{nums}[x] = \textit{nums}[x + 1] nums[x]=nums[x+1]。
对于下标 x x x,可以根据 x x x 的奇偶性以及与 nums [ x ] \textit{nums}[x] nums[x] 相同的元素下标判断只出现一次的元素位于下标 x x x 处、下标 x x x 的左边或下标 x x x 的右边。因此可以使用二分查找得到只出现一次的元素的下标。
用 low \textit{low} low 和 high \textit{high} high 分别表示二分查找的下标范围的下界和上界,初始时 low \textit{low} low 和 high \textit{high} high 分别为数组的最小下标和最大下标。每次查找时,取 mid \textit{mid} mid 为 low \textit{low} low 和 high \textit{high} high 的平均数向下取整,执行如下操作。
-
如果 mid \textit{mid} mid 是偶数且 nums [ mid ] = nums [ mid + 1 ] \textit{nums}[\textit{mid}] = \textit{nums}[\textit{mid} + 1] nums[mid]=nums[mid+1],或 mid \textit{mid} mid 是奇数且 nums [ mid ] = nums [ mid − 1 ] \textit{nums}[\textit{mid}] = \textit{nums}[\textit{mid} - 1] nums[mid]=nums[mid−1],则只出现一次的元素位于下标 mid \textit{mid} mid 的右边,因此在下标范围 [ mid + 1 , high ] [\textit{mid} + 1, \textit{high}] [mid+1,high] 中继续查找。
-
否则,只出现一次的元素位于下标 mid \textit{mid} mid 或其左边,因此在下标范围 [ low , mid ] [\textit{low}, \textit{mid}] [low,mid] 中继续查找。
当 low = high \textit{low} = \textit{high} low=high 时,查找结束,此时 low \textit{low} low 即为只出现一次的元素的下标, nums [ low ] \textit{nums}[\textit{low}] nums[low] 即为只出现一次的元素。
代码
class Solution {public int singleNonDuplicate(int[] nums) {int low = 0, high = nums.length - 1;while (low < high) {int mid = low + (high - low) / 2;if (mid % 2 == 0 && nums[mid] == nums[mid + 1] || mid % 2 == 1 && nums[mid] == nums[mid - 1]) {low = mid + 1;} else {high = mid;}}return nums[low];}
}
复杂度分析
-
时间复杂度: O ( log n ) O(\log n) O(logn),其中 n n n 是数组 nums \textit{nums} nums 的长度。二分查找的范围是数组的全部 n n n 个下标,二分查找的时间复杂度是 O ( log n ) O(\log n) O(logn)。
-
空间复杂度: O ( 1 ) O(1) O(1)。
解法二
思路和算法
由于只出现一次的元素的左边有偶数个元素,因此只出现一次的元素一定位于偶数下标,可以只在偶数下标中二分查找。
由于给定的数组长度是奇数,因此数组的最小下标和最大下标都是偶数,二分查找的下标范围的下界和上界的初始值分别为数组的最小下标和最大下标。每次查找时,取 mid \textit{mid} mid 为 low \textit{low} low 和 high \textit{high} high 的平均数向下取整,如果得到的 mid \textit{mid} mid 是奇数则将 mid \textit{mid} mid 减 1 1 1,确保 mid \textit{mid} mid 是偶数,执行如下操作。
-
如果 nums [ mid ] = nums [ mid + 1 ] \textit{nums}[\textit{mid}] = \textit{nums}[\textit{mid} + 1] nums[mid]=nums[mid+1],则只出现一次的元素位于下标 mid \textit{mid} mid 的右边,因此在下标范围 [ mid + 2 , high ] [\textit{mid} + 2, \textit{high}] [mid+2,high] 中继续查找。
-
否则,只出现一次的元素位于下标 mid \textit{mid} mid 或其左边,因此在下标范围 [ low , mid ] [\textit{low}, \textit{mid}] [low,mid] 中继续查找。
二分查找过程中,每次更新后的下标范围的下界和上界都是偶数,确保只在偶数下标中二分查找。
当 low = high \textit{low} = \textit{high} low=high 时,查找结束,此时 low \textit{low} low 即为只出现一次的元素的下标, nums [ low ] \textit{nums}[\textit{low}] nums[low] 即为只出现一次的元素。
代码
class Solution {public int singleNonDuplicate(int[] nums) {int low = 0, high = nums.length - 1;while (low < high) {int mid = low + (high - low) / 2;if (mid % 2 != 0) {mid--;}if (nums[mid] == nums[mid + 1]) {low = mid + 2;} else {high = mid;}}return nums[low];}
}
复杂度分析
-
时间复杂度: O ( log n ) O(\log n) O(logn),其中 n n n 是数组 nums \textit{nums} nums 的长度。二分查找的范围是数组的 n + 1 2 \dfrac{n + 1}{2} 2n+1 个偶数下标,二分查找的时间复杂度是 O ( log n ) O(\log n) O(logn)。
-
空间复杂度: O ( 1 ) O(1) O(1)。
相关文章:

二分查找题目:有序数组中的单一元素
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:有序数组中的单一元素 出处:540. 有序数组中的单一元素 难度 4 级 题目描述 要求 给定一个仅由整数…...

springboot基于Android的华蓥山旅游导航系统
摘 要 华蓥山旅游导航系统是一款专为华蓥山景区设计的智能导览应用,旨在为用户提供便捷的旅游信息服务。该系统通过整合华蓥山的地理信息、景点介绍、交通状况等数据,实现了对景区的全面覆盖。用户可以通过该系统获取实时的旅游资讯、交流论坛、地图等。…...

面向对象编程(OOP)深度解析:思想、原则与应用
🚀 作者 :“码上有前” 🚀 文章简介 :Java 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 面向对象编程(OOP)深度解析:思想、原则与应用 一、面向对象编程的基本…...

iPhone 17 Air看点汇总:薄至6mm 刷新苹果轻薄纪录
我们姑且将这款iPhone 17序列的超薄SKU称为“iPhone 17 Air”,Jeff Pu在报告中提到,我同意最近关于 iPhone 17超薄机型采用6 毫米厚度超薄设计的传言。 如果这一测量结果被证明是准确的,那么将有几个值得注意的方面。 首先,iPhone…...

「OpenCV交叉编译」ubuntu to arm64
Ubuntu x86_64 交叉编译OpenCV 为 arm64OpenCV4.5.5、cmake version 3.16.3交叉编译器 gcc-arm-10.2-2020.11-x86_64-aarch64-none-linux-gnu 可在arm或linaro官网下载所需版本,本文的交叉编译器可点击链接跳转下载 Downloads | GNU-A Downloads – Arm Developer L…...
Stable Diffusion的解读(二)
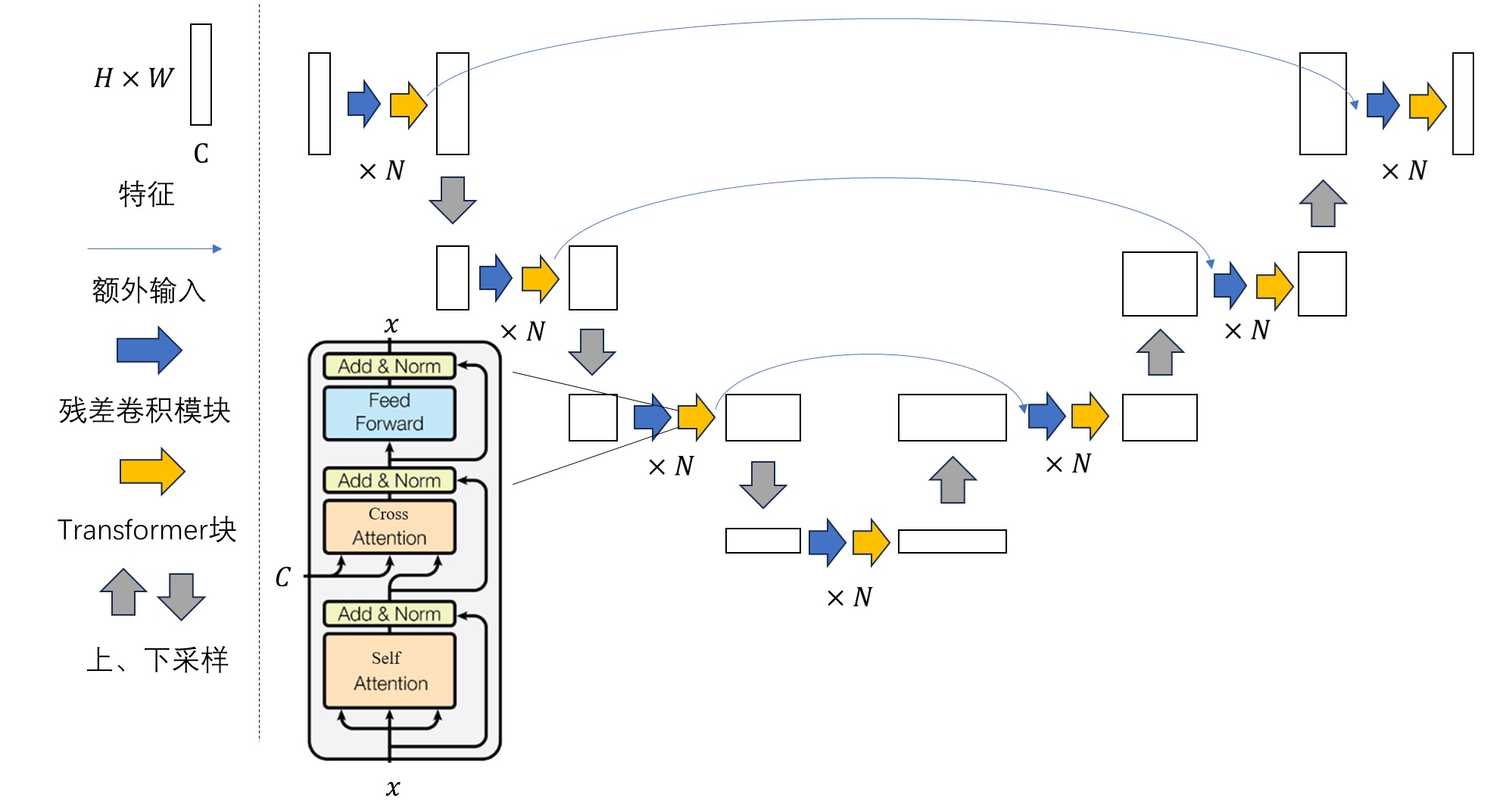
Stable Diffusion的解读(二) 文章目录 Stable Diffusion的解读(二)摘要Abstract一、机器学习部分1. 算法梳理1.1 LDM采样算法1.2 U-Net结构组成 2. Stable Diffusion 官方 GitHub 仓库2.1 安装2.2 主函数2.3 DDIM采样器2.4 Unet 3…...

amd显卡和nVidia显卡哪个好 amd和英伟达的区别介绍
AMD和英伟达是目前市场上最主要的两大显卡品牌,它们各有自己的特点和优势,也有不同的适用场景和用户群体。那么,AMD显卡和英伟达显卡到底哪个好?它们之间有什么区别?我们又该如何选择呢?本文将从以下几个方…...

软件测试—— Selenium 常用函数(一)
前一篇文章:软件测试 —— 自动化基础-CSDN博客 目录 前言 一、窗口 1.屏幕截图 2.切换窗口 3.窗口设置大小 4.关闭窗口 二、等待 1.等待意义 2.强制等待 3.隐式等待 4.显式等待 总结 前言 在前一篇文章中,我们介绍了自动化的一些基础知识&a…...

为什么verilog中递归函数需要定义为automatic?
直接上代码 module automatic_tb;reg [7:0] value;initial begin #0 value < 8d5;#10 $display("result of automatic: %0d", factor_automatic(value));$display("result of static: %0d", factor_static(value));#50 $stop; endfunction reg[7:0] fa…...

23种设计模式-状态(State)设计模式
文章目录 一.什么是状态模式?二.状态模式的结构三.状态模式的应用场景四.状态模式的优缺点五.状态模式的C实现六.状态模式的JAVA实现七.代码解释八.总结 类图: 状态设计模式类图 一.什么是状态模式? 状态模式(State Pattern&…...

EventListener与EventBus
EventListener JDK JDK1.1开始就提供EventListener,一个标记接口,源码如下: /*** A tagging interface that all event listener interfaces must extend.*/ public interface EventListener { }JDK提供的java.util.EventObject࿱…...

Facebook为什么注册失败了?该怎么解决?
有时候用户在尝试注册Facebook账号时可能会遇到各种问题,导致注册失败或遇到困难。小编会为大家分析Facebook注册失败的可能原因,并提供解决方法,帮助大家顺利完成注册流程。 一、Facebook注册失败的可能原因 1. 账号信息问题: …...

前端数据可视化思路及实现案例
目录 一、前端数据可视化思路 (一)明确数据与目标 (二)选择合适的可视化图表类型 (三)数据与图表的绑定及交互设计 (四)页面布局与样式设计 二、具体案例:使用 Ech…...
【DVWA】Brute Force暴力破解实战
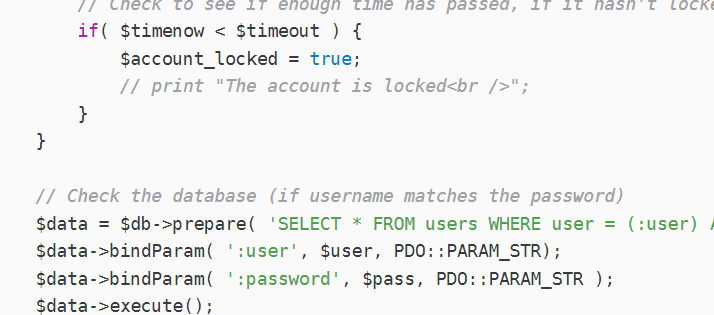
问尔辈 何等样人 自摸心头 再来求我;若汝能 克存忠孝 持身正直 不拜何妨 1.Brute Force(Low) 相关的代码分析 if( isset( $_GET[ Login ] ) ) {// Get username$user $_GET[ username ];// Check the database$query "SELECT * FROM users WHERE user $…...

23种设计模式速记法
前言 在软件开发的过程中,设计模式作为解决常见问题的通用模板,一直是开发者的重要工具。尤其是在面临复杂系统架构和需求变化时,设计模式不仅能够提升代码的可复用性和扩展性,还能大大提高团队之间的协作效率。然而,…...

第7章硬件测试-7.3 功能测试
7.3 功能测试 7.3.1 整机规格测试7.3.2 整机试装测试7.3.3 DFX测试 功能测试包括整机规格、整机试装和整机功能测试,是整机结构和业务相关的测试。 7.3.1 整机规格测试 整机规格测试包括尺寸、重量、温度、功耗等数据。这些测试数据与设计规格进行比对和校验&…...

动态规划子数组系列一>等差数列划分
题目: 解析: 代码: public int numberOfArithmeticSlices(int[] nums) {int n nums.length;int[] dp new int[n];int ret 0;for(int i 2; i < n; i){dp[i] nums[i] - nums[i-1] nums[i-1] - nums[i-2] ? dp[i-1]1 : 0;ret dp[i…...

《Python浪漫的烟花表白特效》
一、背景介绍 烟花象征着浪漫与激情,将它与表白结合在一起,会创造出别具一格的惊喜效果。使用Python的turtle模块,我们可以轻松绘制出动态的烟花特效,再配合文字表白,打造一段专属的浪漫体验。 接下来,让…...

什么是RESTful API,有什么特点
RESTful API 概述 什么是 RESTful API? RESTful API 是基于 Representational State Transfer(表现层状态转移)架构风格的 Web 服务接口。REST 是一种设计风格,而不是具体的协议或标准。它定义了一组约束和最佳实践,…...
友思特新闻 | 友思特荣获广州科技创新创业大赛智能装备行业赛初创组优胜企业!
2024年11月19日,第十三届中国创新创业大赛(广东广州赛区)暨2024年广州科技创新创业大赛智能装备行业赛颁奖典礼隆重举行。 赛事奖项介绍:广州科技创新创业大赛智能装备行业赛 第十三届“中国创新创业大赛(广东广州赛区…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
