c ++零基础可视化——vector
c ++零基础可视化——vector
初始化
vector<int> v0(5); // 0 0 0 0 0
vector<int> v1(5, 1); // 1 1 1 1 1
vector<int> v2{1, 2, 3} // 1 2 3
vector<int> v3(v1); // 1 1 1 1 1
vector<vector<int>> v4(2, vector<int>(8, 3));
// 3 3 3 3 3 3 3 3
// 3 3 3 3 3 3 3 3
auto v5 = vector(2, vector<int>(8, 3));
// 3 3 3 3 3 3 3 3
// 3 3 3 3 3 3 3 3
启发:使用auto可以更好对二位vector进行初始化。
赋值运算,比较运算
vector<int> v0{1, 2, 3};
vector<int> v1;
v1 = v0;
vector<int> v2{1, 2, 4};
v0 < v2;
比较大小:按字典序比较。
vector常用成员函数
v.front()获取vector的第一个元素
v.back()获取vector的最后一个元素
v.size()获取vector的元素个数
v.empty()判断vector是否为空
v.clear()清空vector的数据
v.push_back()将数据塞入vector的末尾
v.pop_back()将数据从vector的末尾移除
v.resize(3)重新定义vector的大小。若比原先小,则删除末尾元素;若比原先大,则用0填充新增的元素;v.resize(5, 1)若有第二个参数,则用第二个参数来填充
v.begin()
v.end()
以下示例仅代表用法,并不是对同一数组进行连续操作,而代表的是每次都对最上面的数组进行操作,即不考虑之前对数组操作的语句对数组的改变。以此来演示语法规则。
vector<int> v{1, 2, 3, 4, 5};
v.erase(v.begin()); //删除1,得到2 3 4 5
v.erase(v.begin() + 1, v.end() + 3) //删除2 3,得到1 4 5
vector<int> v{1, 2, 3};
v.insert(v.begin(), 4); //插入4,得到4 1 2 3
v.insert(v.begin + 1, {4, 5, 6}); //插入4 5 6,得到 1 4 5 6 2 3
vector<int> v1(1, 2, 3);
vector<int> v2(4, 5, 6);
v1.insert(v1.end(), v2.begin(), v2.end()); //插入 4 5 6,得到 1 2 3 4 5 6
题目一【旋转排列】:https://www.luogu.com.cn/problem/B3688
[语言月赛202212] 旋转排列
题目背景
我们称一个数列 p p p 是一个长度为 n n n 的排列,当且仅当 p p p 满足如下条件:
- p p p 的长度为 n n n;
- 1 , 2 , 3 , … n 1, 2, 3, \dots n 1,2,3,…n 这 n n n 个数在 p p p 中均恰好出现一次。
题目描述
对于一个排列 p p p,定义一次“shift”操作是指:将 p p p 里的每一个数字都依次向后移动一位,并把 p p p 的最后一个数字移动到开头去。
例如,若排列 p p p 初始时为 [ 1 , 4 , 2 , 3 ] [1,4,2,3] [1,4,2,3],则“shift”一次以后将变为 [ 3 , 1 , 4 , 2 ] [3,1,4,2] [3,1,4,2]。
现在,给定一个长度为 n n n 的排列 p p p,请你按照如下规定循环操作:
- 对当前的排列 p p p 做一次“shift”操作;
- 输出本次“shift”以后的排列 p p p;
- 判断排列 p p p 的最后一个数字是否是 n n n,如果是,则结束循环操作;否则回到 1 1 1 继续操作。
提示:请严格按照题目给出的顺序进行循环操作。
输入格式
第一行是一个整数,表示排列 p p p 的长度 n n n。
第二行有 n n n 个整数表示排列 p p p,第 i i i 个整数表示 p i p_i pi。
输出格式
对于每次操作的第二条“输出”操作,请你输出一行 n n n 个整数,按顺序表示当前排列的每个数,一行中相邻两个数之间用一个空格隔开。
样例 #1
样例输入 #1
4
1 4 2 3
样例输出 #1
3 1 4 2
2 3 1 4
样例 #2
样例输入 #2
3
1 2 3
样例输出 #2
3 1 2
2 3 1
1 2 3
样例 #3
样例输入 #3
10
1 7 6 5 8 4 3 9 10 2
样例输出 #3
2 1 7 6 5 8 4 3 9 10
提示
样例 2 解释
对 p = [ 1 , 2 , 3 ] p = [1, 2, 3] p=[1,2,3],按如下顺序进行循环操作:
- 进行一次“shift”操作, p p p 变为 [ 3 , 1 , 2 ] [3,1,2] [3,1,2];
- 输出当前的排列 p p p,故输出第一行为
3 1 2; - 判断 p 3 = 2 ≠ 3 p_3 = 2 \neq 3 p3=2=3,故继续循环操作;
- 进行一次“shift”操作, p p p 变为 [ 2 , 3 , 1 ] [2,3,1] [2,3,1];
- 输出当前的排列 p p p,故输出第二行为
2 3 1; - 输出判断 p 3 = 1 ≠ 3 p_3 = 1 \neq 3 p3=1=3,故继续循环操作;
- 进行一次“shift”操作, p p p 变为 [ 1 , 2 , 3 ] [1,2,3] [1,2,3];
- 输出当前的排列 p p p,故输出第二行为
1 2 3; - 输出判断 p 3 = 3 = 3 p_3 = 3 =3 p3=3=3,故停止循环;
数据规模与约定
各测试点的信息如下表:
| 测试点编号 | $n = $ | 特殊约定 |
|---|---|---|
| 1 1 1 | 1 1 1 | 无 |
| 2 2 2 | 2 2 2 | 无 |
| 3 3 3 | 3 3 3 | 无 |
| 4 ∼ 6 4 \sim 6 4∼6 | 2000 2000 2000 | p n − 1 = n p_{n - 1} = n pn−1=n |
| 7 ∼ 10 7 \sim 10 7∼10 | 2000 2000 2000 | 无 |
对全部的测试点,保证 1 ≤ p i ≤ n ≤ 2000 1 \leq p_i \leq n \leq 2000 1≤pi≤n≤2000, p p p 是长度为 n n n 的排列。
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;vector<int> nums(n);for(auto& x : nums) cin >> x;do {int back = nums.back();nums.pop_back();nums.insert(nums.begin(), back);for(auto& x : nums) cout << x << " ";cout << endl;}while(nums.back() != n);return 0;
}
启发:使用do while语句可以完美契合题意;注意精简代码。
问题二【进制转换】:https://www.luogu.com.cn/problem/B3849
[GESP样题 三级] 进制转换
题目描述
小美刚刚学习了十六进制,她觉得很有趣,想到是不是还有更大的进制呢?在十六进制中,用 A 表示 10 10 10、F 表示 15 15 15。如果扩展到用 Z 表示 35 35 35,岂不是可以表示 36 36 36 进制数了嘛!
所以,你需要帮助她写一个程序,完成十进制转 R R R 进制( 2 ≤ R ≤ 36 2\le R\le 36 2≤R≤36)的工作。
输入格式
输入两行,第一行包含一个正整数 N N N,第二行包含一个正整数 R R R,保证 1 ≤ N ≤ 1 0 6 1\le N\le 10^6 1≤N≤106。
输出格式
输出一行,为 N N N 的 R R R 进制表示。
样例 #1
样例输入 #1
123
25
样例输出 #1
4N
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, R;cin >> n >> R;vector<int> digit;while(n) {digit.push_back(n % R);n /= R;}reverse(digit.begin(), digit.end());for(auto& x : digit) {if(x < 10) {cout << x;} else {cout << char(x - 10 + 'A');}}return 0;
}
启发:隐式转换;如何取出数字的每一位。
问题三【排排队,做游戏】:https://www.luogu.com.cn/problem/B3766
[语言月赛202305] 排排队,做游戏
题目描述
n n n 名小朋友站成了一排,他们会按照体育老师的指令进行排队做游戏。
体育老师会向他们依次下发 T T T 条指令,每条指令包含一个小于等于 n n n 的正整数 k k k。
对某一条指令,小朋友们会按照如下步骤进行排队:
- 该指令下发前,排在从左到右数第 1 , k + 1 , 2 k + 1 , ⋯ 1, k + 1, 2k + 1, \cdots 1,k+1,2k+1,⋯ 位的小朋友,在指令下发后应该依次站在从左到右第 1 , 2 , ⋯ 1, 2, \cdots 1,2,⋯ 个位置。
- (如果 k ≥ 2 k \geq 2 k≥2)该指令下发前,排在从左到右数第 2 , k + 2 , 2 k + 2 , ⋯ 2, k + 2, 2k + 2, \cdots 2,k+2,2k+2,⋯ 位的小朋友,在指令下发后应该依次站在第一步中的小朋友(原来从左到右数第 1 , k + 1 , 2 k + 1 , ⋯ 1, k + 1, 2k + 1, \cdots 1,k+1,2k+1,⋯ 位的小朋友)右边的第 1 , 2 , ⋯ 1, 2, \cdots 1,2,⋯ 个位置。
- (如果 k ≥ 3 k \geq 3 k≥3) 3 , k + 3 , 2 k + 3 , ⋯ 3, k + 3, 2k + 3, \cdots 3,k+3,2k+3,⋯ 的小朋友站在第二步的小朋友右边,(如果 k ≥ 4 k \geq 4 k≥4) 4 , k + 4 , 2 k + 4 , ⋯ 4, k + 4, 2k + 4, \cdots 4,k+4,2k+4,⋯ 的小朋友站在 3 , k + 3 , 2 k + 3 , ⋯ 3, k + 3, 2k + 3, \cdots 3,k+3,2k+3,⋯ 的小朋友右边,以此类推,直至所有小朋友都被安排过(无论位置是否有变化)。
我们依次给出初始时从左到右每个小朋友的学号 a 1 , a 2 , ⋯ , a n a _ 1, a _ 2, \cdots, a _ n a1,a2,⋯,an。现在我们想要知道,在 T T T 次指令下发后,从左到右每个小朋友的学号依次是什么。
输入格式
输入共三行。
第一行为两个整数 n , T n, T n,T,代表小朋友的数量和指令数。
第二行为 n n n 个整数 a 1 , a 2 , ⋯ , a n a _ 1, a _ 2, \cdots, a _ n a1,a2,⋯,an,代表初始时从左到右每个小朋友的学号。
第三行为 T T T 个整数,代表体育老师下发的 T T T 条指令。
输出格式
输出共一行 n n n 个整数,代表在 T T T 次指令下发后,从左到右每个小朋友的学号。
样例 #1
样例输入 #1
8 4
72818 21895123 25718513 289523 52783 18520 295123 285952
1 2 3 5
样例输出 #1
72818 285952 295123 52783 18520 289523 25718513 21895123
样例 #2
样例输入 #2
4 1
28910 65363 274993 653516
2
样例输出 #2
28910 274993 65363 653516
提示
样例 1 解释
为了方便表述,我们先按照初始时的排队顺序将小朋友依次编号为 1 , 2 , ⋯ , 8 1, 2, \cdots, 8 1,2,⋯,8。下表为初始时及每次指令后队列中每个位置上的小朋友的编号。
| 队列中的位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 初始时 | 1 1 1 | 2 2 2 | 3 3 3 | 4 4 4 | 5 5 5 | 6 6 6 | 7 7 7 | 8 8 8 |
| 第一个指令后 | 1 1 1 | 2 2 2 | 3 3 3 | 4 4 4 | 5 5 5 | 6 6 6 | 7 7 7 | 8 8 8 |
| 第二个指令后 | 1 1 1 | 3 3 3 | 5 5 5 | 7 7 7 | 2 2 2 | 4 4 4 | 6 6 6 | 8 8 8 |
| 第三个指令后 | 1 1 1 | 7 7 7 | 6 6 6 | 3 3 3 | 2 2 2 | 8 8 8 | 5 5 5 | 4 4 4 |
| 第四个指令后 | 1 1 1 | 8 8 8 | 7 7 7 | 5 5 5 | 6 6 6 | 4 4 4 | 3 3 3 | 2 2 2 |
样例 2 解释
前三个小朋友的学号分别是三个出题人的洛谷 UID。
有人说学号是随机生成的,学号可不是随机生成的啊。
数据规模与约定
对于 100 % 100\% 100% 的数据,保证 1 ≤ n ≤ 1 0 4 1 \leq n \leq 10 ^ 4 1≤n≤104, 1 ≤ T ≤ 1 0 4 1 \leq T \leq 10 ^ 4 1≤T≤104, 1 ≤ k ≤ n 1 \leq k \leq n 1≤k≤n, 1 ≤ a i ≤ 1 0 9 1 \leq a _ i \leq 10 ^ 9 1≤ai≤109。
| 测试点编号 | n n n | T T T | 特殊限制 |
|---|---|---|---|
| 1 1 1 | = 1 = 1 =1 | ≤ 5 × 1 0 3 \leq 5 \times 10 ^ 3 ≤5×103 | 无 |
| 2 ∼ 4 2 \sim 4 2∼4 | ≤ 10 \leq 10 ≤10 | ≤ 10 \leq 10 ≤10 | 无 |
| 5 5 5 | ≤ 5 × 1 0 3 \leq 5 \times 10 ^ 3 ≤5×103 | ≤ 5 × 1 0 3 \leq 5 \times 10 ^ 3 ≤5×103 | k = 1 k = 1 k=1 |
| 6 ∼ 8 6 \sim 8 6∼8 | ≤ 5 × 1 0 3 \leq 5 \times 10 ^ 3 ≤5×103 | ≤ 5 × 1 0 3 \leq 5 \times 10 ^ 3 ≤5×103 | 无 |
| 9 ∼ 10 9 \sim 10 9∼10 | ≤ 1 0 4 \leq 10 ^ 4 ≤104 | ≤ 1 0 4 \leq 10 ^ 4 ≤104 | 无 |
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, T;cin >> n >> T;vector<int> nums(n);vector<int> newNums;for(auto& x : nums) {cin >> x;}while(T --) {int k;cin >> k;for(int i = 0; i < k; i ++) {for(int j = i; j < n; j += k) {newNums.push_back(nums[j]);}}nums = newNums;newNums.clear();}for(auto& x : nums) {cout << x << " ";}return 0;
}
启发:每次选人相当于分成k组。比如:当k = 2时,就会先选出索引为0 2 4 6 8…的人,再选出1 3 5 7 9…的人,先选出来的排在前面,后选出的排在后面。对题面的理解:每次选出的人都应该在第一个人的索引上加上k的倍数。
每次排出新的队伍,就保存在newNums中,再将新队伍newNums赋值给nums,最后将newNums清空。
要加深对数学型题面的理解。本题面加深了我的理解力。
问题四【你的牌太多了】:https://www.luogu.com.cn/problem/B3745
[语言月赛202304] 你的牌太多了
题目描述
笨蛋扶苏和坏蛋小 F 在打一种很新的牌。
初始时,扶苏和小 F 手中各有 n n n 张牌。每张牌有一个花色 f f f 和一个点数 p p p。在本题中,花色是不超过 m m m 的正整数,点数是不超过 r r r 的正整数。
打牌共会进行 n n n 轮,每轮扶苏会从手中选择一张牌打出。小 F 会从当前手牌中,选择与扶苏本轮打出的牌花色相同且点数大于扶苏打出的牌中点数最小的一张打出。如果这样的牌不存在,那么小 F 不会接牌(也就是不会出牌)。
注意,无论小 F 打出什么牌,本轮都立即结束,扶苏不会继续接牌,而是会开启下一轮出牌。
给出扶苏的出牌顺序,请你求出小 F 最终手里剩了几张牌。
输入格式
第一行是三个整数,表示一个人的手牌数 n n n,花色的上界 m m m 和点数的上界 r r r。
第二行有 n n n 个整数,第 i i i 个整数表示扶苏第 i i i 张牌的花色 f 1 i f1_i f1i。
第三行有 n n n 个整数,第 i i i 个整数表示扶苏第 i i i 张牌的点数 p 1 i p1_i p1i。
第四行有 n n n 个整数,第 i i i 个整数表示小 F 第 i i i 张牌的花色 f 2 i f2_i f2i。
第五行有 n n n 个整数,第 i i i 个整数表示小 F 第 i i i 张牌的点数 p 2 i p2_i p2i。
第六行是一个长度为 n n n 的排列,描述扶苏的出牌情况。第 i i i 个整数 p i p_i pi 表示扶苏第 i i i 轮出了第 p i p_i pi 张牌。
输出格式
输出一行一个整数,表示坏蛋小 F 结束时手里剩余的牌数。
样例 #1
样例输入 #1
3 1 2
1 1 1
1 2 1
1 1 1
2 2 1
2 3 1
样例输出 #1
1
样例 #2
样例输入 #2
3 2 2
1 2 1
1 1 1
1 2 1
2 2 2
1 2 3
样例输出 #2
0
提示
样例 1 解释
小 F 花色为 1 1 1 且点数也为 1 1 1 的牌管不住任何牌。其余牌都被打出去了。
数据规模与约定
- 对于 10 % 10\% 10% 的数据, r = 1 r = 1 r=1;
- 对于 20 % 20\% 20% 的数据, n = 1 n = 1 n=1;
- 对于 50 % 50\% 50% 的数据, m = 1 m = 1 m=1;
- 对于 100 % 100\% 100% 的数据, 1 ≤ n , m , r ≤ 100 1 \leq n,m,r \leq 100 1≤n,m,r≤100, 1 ≤ f 1 i , f 2 i ≤ m 1 \leq f1_i, f2_i \leq m 1≤f1i,f2i≤m, 1 ≤ p 1 i , p 2 i ≤ r 1 \leq p1_i, p2_i \leq r 1≤p1i,p2i≤r。 1 ≤ p i ≤ n 1 \leq p_i \leq n 1≤pi≤n, p p p 是长度为 n n n 的排列。
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m, r;cin >> n >> m >> r;vector<int> f1(n), p1(n), f2(n), p2(n);for(auto& x : f1) cin >> x;for(auto& x : p1) cin >> x;for(auto& x : f2) cin >> x;for(auto& x : p2) cin >> x;while(n --) {int order;cin >> order;order --;int idx = -1;for(int i = 0; i < f2.size(); i ++) {if(f2[i] == f1[order] && p2[i] > p1[order]) {if(idx == -1 || p2[i] < p2[idx]) {idx = i;}}}if(idx != -1) {f2.erase(f2.begin() + idx);p2.erase(p2.begin() + idx);}}cout << f2.size() << endl;return 0;
}
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m, r;cin >> n >> m >> r;vector<int> p1(n), f1(n), p2(n), f2(n);vector<int> output(n);for(int i = 0; i < n; i ++) {cin >> f1[i];}for(int i = 0; i < n; i ++) {cin >> p1[i];}for(int i = 0; i < n; i ++) {cin >> f2[i];}for(int i = 0; i < n; i ++) {cin >> p2[i];}for(int i = 0; i < n; i ++) {cin >> output[i];}int cnt = 0;for(int i = 0; i < n; i ++) {int outF = f1[output[i] - 1], outP = p1[output[i] - 1];vector<pair<int, int>> temp;for(int j = 0; j < n; j ++) {if(f2[j] == outF && f2[j] != -1 && p2[j] > outP) {temp.push_back({f2[j], p2[j]}); // F P}}int maxMin = 101;for(auto& x : temp) {if(x.second > outP && x.second < maxMin) {maxMin = x.second;}}if(maxMin != 101) {for(auto& x : temp) {if(x.second == maxMin) {for(int k = 0; k < n; k ++) {if(f2[k] == x.first && p2[k] == x.second) {f2[k] = p2[k] = -1;break;}}break;}}cnt ++;}temp.clear();}cout << n - cnt << endl;return 0;
}
启发:模拟题,题目不难,显然上面的代码精简。但我的方法很冗长复杂,究其原因还是没有熟练掌握vector的精髓之处。我与其对比,纵观我的代码,我总是想要存储数据,但这完全不必要。而且应用的函数也很少,总是用push_back()。这导致我的方法不够好。
题目五【Coin Selection G】:https://www.luogu.com.cn/problem/B3723
[语言月赛202303] Coin Selection G
题目描述
Farmer John 和 Bessie 正在一起玩硬币选择游戏。
初始时桌面上有 n n n 枚硬币,每枚硬币有一个面额,我们使用 a 1 , a 2 , ⋯ , a n a _ 1, a _ 2, \cdots, a _ n a1,a2,⋯,an 分别代表第 1 , 2 , ⋯ , n 1, 2, \cdots, n 1,2,⋯,n 枚硬币的面额。
他们还各有一个属于自己的钱包,初始时,钱包都是空的。
从 Farmer John 开始,双方轮流操作。每次操作中,当前的操作者会从桌面上剩余的硬币中选择面值不超过当前自己钱包中硬币的总面额的硬币中面额最大的一枚硬币,把它从桌子上拿走,放到自己的钱包里。如果桌面上剩余的所有硬币面值都超过了自己钱包里已有硬币的总面额,那么选择剩余的所有硬币中面额最小的一个。
当桌面上没有硬币时,游戏结束。
请你分别求出, 游戏结束后,Farmer John 和 Bessie 钱包里硬币的总面额。
输入格式
第一行为一个整数,代表初始时桌面上的硬币的数量 n n n。
第二行为 n n n 个整数 a 1 , a 2 , ⋯ , a n a _ 1, a _ 2, \cdots, a _ n a1,a2,⋯,an,分别代表第 1 , 2 , ⋯ , n 1, 2, \cdots, n 1,2,⋯,n 枚硬币的面额。
输出格式
输出共一行两个整数,第一个整数表示 Farmer John 最终钱包里的总面额,第二个整数表示 Bessie 最终钱包里硬币的总面额,两个整数之间使用一个空格隔开。
样例 #1
样例输入 #1
2
3 2
样例输出 #1
2 3
样例 #2
样例输入 #2
5
1 2 3 4 5
样例输出 #2
9 6
提示
样例 1 解释
Farmer John 开始时「自己钱包中硬币的总面额」为 0 0 0,小于桌面上的任何一枚硬币,因此他只能选择剩下的所有硬币中面值最小的一个,为 2 2 2。
接下来 Bessie「自己钱包中硬币的总面额」为 0 0 0,小于桌面上的任何一枚硬币,因此只能选择剩下的所有硬币中面值最小的一个,为 3 3 3。
数据规模与约定
- 对 20 % 20\% 20% 的数据,保证 n ≤ 2 n \leq 2 n≤2。
- 另有 20 % 20\% 20% 的数据,保证 a i = 1 a_i = 1 ai=1。
- 对 60 % 60\% 60% 的数据,保证 n ≤ 100 n \leq 100 n≤100。
- 对 100 % 100\% 100% 的数据,保证 1 ≤ n ≤ 1 0 3 1 \leq n \leq 10^3 1≤n≤103, 1 ≤ a i ≤ 1 0 16 1 \leq a_i \leq 10^{16} 1≤ai≤1016。
provider:一扶苏一
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;vector<LL> nums(n);for(auto& x : nums) cin >> x;LL sum1 = 0, sum2 = 0;auto op = [&](LL& sum) -> void {int idx = -1;for(int i = 0; i < nums.size(); i ++) {if(nums[i] <= sum) {if(idx == -1 || nums[idx] < nums[i]) {idx = i;}}}if(idx == -1) {LL minn = *min_element(nums.begin(), nums.end());auto it = find(nums.begin(), nums.end(), minn);nums.erase(it);sum += minn;} else {sum += nums[idx];nums.erase(nums.begin() + idx); }};while(nums.size() != 0) {op(sum1);if(nums.size() == 0) break;op(sum2);}cout << sum1 << " " << sum2 << endl;return 0;}
启发:这段代码维护idx使用过多次,需要加深理解。
int idx = -1;
for(int i = 0; i < nums.size(); i ++) {if(nums[i] <= sum) {if(idx == -1 || nums[idx] < nums[i]) {idx = i;}}
}
题目六【惊蛰】:https://www.luogu.com.cn/problem/B3711
[语言月赛202302] 惊蛰
题目描述
给定一个正整数,规定一次操作为选定 l , r l,r l,r,删去所有从后往前数第 l ∼ r l\sim r l∼r 位的数字,并且将剩下的数字组成一个新的正整数。如 123456 123456 123456 删去从后往前数的第 2 ∼ 3 2\sim 3 2∼3 位就会变成 1236 1236 1236。
现在有 T T T 组询问,每次询问给定一个正整数 n n n,你需要回答:对于这个正整数,能否通过最多一次操作(不操作也算)将其变为 4 4 4 的倍数。
但是请注意,不能把所有的数位全都删完。
输入格式
输入共 T + 1 T+1 T+1 行。
输入的第一行,一个正整数 T T T。
接下来 T T T 行,每行一个正整数 n n n。保证 n n n 不包含前导零。
输出格式
输出共 T T T 行。
对于 T T T 组数据,每组数据需要输出 1 1 1 行,表示问题的答案。若可以,输出 Yes,不可以,输出 No。
样例 #1
样例输入 #1
3
234
1
286
样例输出 #1
Yes
No
Yes
样例 #2
样例输入 #2
1
2386
样例输出 #2
Yes
提示
样例 1 解释
对第一组数据:删去从后往前数第 2 ∼ 3 2\sim 3 2∼3 位,剩下的数是 4 4 4,是 4 4 4 的倍数。
对第二组数据:可以证明没有任何一种方案能够达成目标。
对第三组数据:删去从后往前数第 1 1 1 位,剩下的数是 28 28 28,是 4 4 4 的倍数。
数据范围
对于前 10 % 10\% 10% 的数据,保证 1 ≤ n ≤ 9 1\le n\le 9 1≤n≤9。
对于前 30 % 30\% 30% 的数据,保证 1 ≤ T ≤ 10 , 1 ≤ n ≤ 100 1\le T\le 10,1\le n\le 100 1≤T≤10,1≤n≤100。
对于另外 10 % 10\% 10% 的数据,保证 T = 1 T=1 T=1。
对于前 60 % 60\% 60% 的数据,保证 1 ≤ T ≤ 10 , 1 ≤ n ≤ 1 0 9 1\le T\le 10,1\le n\le 10^9 1≤T≤10,1≤n≤109。
对于 100 % 100\% 100% 的数据, 1 ≤ T ≤ 1 0 2 , 1 ≤ n ≤ 1 0 18 1\le T\le 10^2,1\le n\le 10^{18} 1≤T≤102,1≤n≤1018。
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"void solve() {LL n;cin >> n;vector<int> digits;if(n % 4 == 0) {cout << "Yes" << endl;return;}while(n) {digits.push_back(n % 10);n /= 10;}reverse(digits.begin(), digits.end());bool ok = false;for(int i = 0; i < digits.size() && !ok; i ++) {for(int j = i + 1; j <= digits.size() && !ok; j ++) {auto temp = digits;temp.erase(temp.begin() + i, temp.begin() + j);if(temp.size() == 0) {continue;}LL sum = 0;for(auto& x : temp) {sum = sum * 10 + x;}if(sum % 4 == 0) {ok = true;}}}if(ok) {cout << "Yes" << endl;} else {cout << "No" << endl;}return;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int T;cin >> T;while(T --) {solve();}return 0;
}
启发:对删除数位的枚举需要理解。且同时break掉两层循环只需bool found = false,并将found加入for循环的条件中。
题目七【超链接】:https://www.luogu.com.cn/problem/B3765
[语言月赛202305] 超链接
题目描述
在某局域网中,一共有 N N N 个网页,依次从 1 1 1 编号到 N N N。
每个网页上都有一些超链接,第 i i i 个网页上一共有 T i T_i Ti 个超链接,依次指向 A i , 1 , ⋯ , A i , T i A_{i,1},\cdots,A_{i,T_i} Ai,1,⋯,Ai,Ti 号网页。
某 E 现在从 1 1 1 号网页开始,点击不超过两次超链接,一共能到达多少网页?
输入格式
输入共 N + 1 N+1 N+1 行。
输入的第一行为一个整数 N N N。
接下来第 i i i 行,第一个数为 T i T_i Ti。接下来 T i T_i Ti 个数,每个数代表一个超链接指向的网页。
输出格式
输出一行一个整数,代表你的答案。
样例 #1
样例输入 #1
6
2 2 3
3 3 4 1
2 4 5
1 6
1 6
1 5
样例输出 #1
5
提示
样例解释
- 点击 0 0 0 次: 1 1 1 号页面;
- 点击 1 1 1 次: 2 , 3 2,3 2,3 号页面;
- 点击 2 2 2 次: 1 , 2 , 3 , 4 , 5 1, 2, 3, 4,5 1,2,3,4,5 号页面。
共 5 5 5 个页面。
数据规模与约定
- 对于 30 % 30\% 30% 的测试数据, T i = 1 T_i = 1 Ti=1;
- 对于 100 % 100\% 100% 的测试数据, 1 ≤ N ≤ 1000 1 \le N \le 1000 1≤N≤1000, 0 ≤ T i ≤ 100 0 \le T_i \le 100 0≤Ti≤100, 1 ≤ A i , j ≤ N 1 \le A_{i,j} \le N 1≤Ai,j≤N,同一个网页中不同超链接指向的网页编号不同,不保证不存在指向自己的超链接。
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int n;cin >> n;vector<vector<int>> a(n);for(auto& x : a) {int m;cin >> m;x.resize(m);for(auto& y : x) {cin >> y;}}a.insert(a.begin(), vector<int>());vector<bool> st(n + 1, false);int cnt = 0;st[1] = true;cnt ++;for(int i = 0; i < a[1].size(); i ++) {int x = a[1][i];if(!st[x]) {st[x] = true;cnt ++;}for(int j = 0; j < a[x].size(); j ++) {int y = a[x][j];;if(!st[y]) {st[y] = true;cnt ++;}}}cout << cnt << endl;return 0;
}
启发:若需要输入的数据从索引为1处开始,可以输入完成之后在最前面insert。
题目八【洛谷评测机模拟器】:https://www.luogu.com.cn/problem/B3746
[语言月赛202304] 洛谷评测机模拟器
题目背景
现在假装你是洛谷评测机。这一天,洛谷同时进行了 PION 自测、SCP 自测、ION 自测等等比赛。成千上万的评测落到了你的身上!
题目描述
现在已经知道你有 n n n 个相同性能的评测节点,它们被分别标号为 1 , 2 , ⋯ , n 1, 2, \cdots, n 1,2,⋯,n。一个评测节点在同一时间只能处理一个评测任务。
在某一时刻, m m m 个评测任务同时涌入了你。我们将这些任务分别标号为 1 , 2 , ⋯ , m 1, 2, \cdots, m 1,2,⋯,m。这些评测任务需要的评测时间分别为 t 1 , t 2 , ⋯ , t m t _ 1 , t _ 2, \cdots, t _ m t1,t2,⋯,tm。每个评测任务需要且仅需要一个评测节点来运行,因此你会按照如下方式按照 1 ∼ m 1 \sim m 1∼m 的顺序依次将这些评测任务分配到评测节点上:
对于某个耗时 t i t _ i ti 的评测任务,你需要找到目前累积评测时间最小的评测节点将任务放入。如果有多个评测节点累积评测时间相同且最小,则找一个标号最小的节点将任务放入。
「累积评测时间」定义:假设对于某个评测节点,其被分配了 a 1 , a 2 , ⋯ , a k a _ 1, a _ 2, \cdots, a _ k a1,a2,⋯,ak 共 k k k 个任务。那么这个评测节点的「累积评测时间」就是 t a 1 + t a 2 + ⋯ + t a k t _ {a _ 1} + t _ {a _ 2} + \cdots + t _ {a _ k} ta1+ta2+⋯+tak。显然的,如果某个评测节点从未被分配过这 m m m 个任务中的任何一个,那么这个评测节点的「累积评测时间」是 0 0 0。
现在,你需要统计出,你的这 n n n 个评测节点分别接受了哪一些评测任务。
输入格式
输入共两行。
第一行为两个整数 n , m n, m n,m,代表评测节点数量和评测任务数量。
第二行为 m m m 个整数 t 1 , t 2 , ⋯ , t m t _ 1, t _ 2, \cdots, t _ m t1,t2,⋯,tm,依次代表这 m m m 个评测任务的所需时间。
输出格式
输出共 n n n 行,每行若干个整数,两两之间以一个空格隔开。
对于第 i i i 行,输出第 i i i 个评测节点接受的评测任务编号从小到大排序后的结果。如果第 i i i 个评测节点没有被分配任务,那么输出一行一个 0 0 0。
样例 #1
样例输入 #1
5 10
13 50 90 38 60 64 60 77 6 24
样例输出 #1
1 6
2 8
3
4 7
5 9 10
样例 #2
样例输入 #2
12 7
85 99 82 90 14 11 15
样例输出 #2
1
2
3
4
5
6
7
0
0
0
0
0
提示
数据规模与约定
对于 100 % 100\% 100% 的数据,保证 1 ≤ n , m ≤ 5 × 1 0 3 1 \leq n, m \leq 5 \times 10 ^ 3 1≤n,m≤5×103, 0 ≤ t i ≤ 1 0 9 0 \leq t _ i \leq 10 ^ 9 0≤ti≤109。
| 测试点编号 | n ≤ n \leq n≤ | m ≤ m \leq m≤ | 特殊性质 |
|---|---|---|---|
| 1 ∼ 2 1 \sim 2 1∼2 | 10 10 10 | 10 10 10 | 无 |
| 3 ∼ 4 3 \sim 4 3∼4 | 5 × 1 0 3 5 \times 10 ^ 3 5×103 | 5 × 1 0 3 5 \times 10 ^ 3 5×103 | t i = 0 t _ i = 0 ti=0 |
| 5 ∼ 6 5 \sim 6 5∼6 | 5 × 1 0 3 5 \times 10 ^ 3 5×103 | 5 × 1 0 3 5 \times 10 ^ 3 5×103 | t i = 1 t _ i = 1 ti=1 |
| 7 ∼ 10 7 \sim 10 7∼10 | 5 × 1 0 3 5 \times 10 ^ 3 5×103 | 5 × 1 0 3 5 \times 10 ^ 3 5×103 | 无 |
简短的代码:
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int n, m;cin >> n >> m;vector<LL> sum(n);vector<vector<int>> assignment(n);int number = 1;while(m --) {int t;cin >> t;int idx = 0;for(int i = 1; i < sum.size(); i ++) {if(sum[i] < sum[idx]) idx = i;}sum[idx] += t;assignment[idx].push_back(number ++);} for(auto& x : assignment) {if(x.size() == 0) {cout << 0 << endl;}else {for(auto& y : x) {cout << y << " ";}cout << endl;}}return 0;
}
冗长的代码:
#include <bits/stdc++.h>using namespace std;using LL = long long;#define endl "\n"int main() {ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int n, m;cin >> n >> m;vector<LL> t(m);for(auto& x : t) cin >> x;t.insert(t.begin(), -1);vector<LL> node(n, 0);vector<vector<int>> assignment(n);for(int i = 1; i <= m; i ++) {LL time = t[i];vector<int> mini;LL mint = *min_element(node.begin(), node.end());for(int j = 0; j < node.size(); j ++) {if(node[j] == mint) mini.push_back(j);}int idx = *min_element(mini.begin(), mini.end());node[idx] += time;assignment[idx].push_back(i);}for(int i = 0; i < n; i ++) {int sz = assignment[i].size();if(sz != 0) {for(int j = 0; j < sz; j ++) {cout << assignment[i][j] << " ";}cout << endl;}else {cout << 0 << endl;}}return 0;
}
启发:我的方法较为繁琐。其实不用去存储t[m],而是去维护两个数组sum(n) 和assignment(n)就足够了。
其中对idx的维护需要加深理解。
相关文章:

c ++零基础可视化——vector
c 零基础可视化——vector 初始化 vector<int> v0(5); // 0 0 0 0 0 vector<int> v1(5, 1); // 1 1 1 1 1 vector<int> v2{1, 2, 3} // 1 2 3 vector<int> v3(v1); // 1 1 1 1 1 vector<vector<int>> v4(2, vect…...

Centos 7 安装 Docker 最新版本
文章目录 一、卸载旧版本二、安装最新版本docker三、问题解决3.1 启动docker报错3.2 启动容器报错 一、卸载旧版本 #如果之前安装过旧版本的Docker,可以使用下面命令卸载 yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest …...

构建高效在线教育:SpringBoot课程管理系统
1系统概述 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及,互联网成为人们查找信息的重要场所,二十一世纪是信息的时代,所以信息的管理显得特别重要。因此,使用计算机来管理在线课程管理系统的相关信息成为必然。开发…...

二进制与网络安全的关系
二进制与网络安全的关系 声明! 学习视频来自B站up主 泷羽sec 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章,笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其他均与本人以…...

【计算机网络】网段划分
一、为什么有网段划分 IP地址 网络号(目标网络) 主机号(目标主机) 网络号: 保证相互连接的两个网段具有不同的标识 主机号: 同一网段内,主机之间具有相同的网络号,但是必须有不同的主机号 互联网中的每一台主机,都要隶属于某一个子网 -&…...

VB、VBS、VBA的区别及作用
VB、VBS 和 VBA 是三种与微软 Visual Basic 相关的编程语言或环境,它们在功能和用途上有所不同: # Visual Basic (VB) Visual Basic 是一种面向对象的编程语言,最初由微软公司开发。它是一种高级编程语言,旨在简化开发过程&…...
与时间序列预测)
深度学习中的循环神经网络(RNN)与时间序列预测
一、循环神经网络(RNN)简介 循环神经网络(Recurrent Neural Networks,简称RNN)是一种专门用于处理序列数据的神经网络架构。与传统神经网络不同,RNN具有内部记忆能力,能够捕捉数据中的时间依赖…...
详解)
Unity 设计模式-原型模式(Prototype Pattern)详解
原型模式 (Prototype Pattern) 原型模式 (Prototype Pattern) 是一种创建型设计模式,它允许通过复制现有的对象来创建新对象,而不是通过直接实例化类。这意味着你可以通过克隆原型对象来生成新的实例,而不必依赖类的构造函数。该模式的核心思…...

如何在 RK3568 Android 11 系统上排查以太网问题
1. 硬件连接检查 在进行软件诊断之前,首先确保所有硬件连接正常: 确认网线可靠插入设备的以太网端口。交换机、路由器中与设备连接的端口是否正常工作。若有可能,尝试更换网线或使用其他端口。2. 使用命令行工具进行基本检查 检查网络接口状态 连接设备并使用 ADB 或终端…...
如何在WPF中嵌入其它程序
在WPF中嵌入其它程序,这里提供两种方案 一、使用WindowsFormHost 使用步骤如下 1、添加WindowsFormsIntegration和System.Windows.Forms引用 2、在界面上放置WindowsFormHost和System.Windows.Forms.Panel 1 <Grid> 2 <WindowsFormsHost> 3…...

大模型呼入系统是什么?
大模型呼入系统是什么? 作者:开源呼叫中心系统 FreeIPCC,Github地址:https://github.com/lihaiya/freeipcc 在呼叫中心领域,大模型呼入是指利用大型语言模型(如GPT等)处理客户呼入的电话请求&a…...

Flutter:SlideTransition位移动画,Interval动画延迟
配置vsync,需要实现一下with SingleTickerProviderStateMixinclass _MyHomePageState extends State<MyHomePage> with SingleTickerProviderStateMixin{// 定义 AnimationControllerlate AnimationController _controller;overridevoid initState() {super.…...

【Elasticsearch入门到落地】2、正向索引和倒排索引
接上篇《1、初识Elasticsearch》 上一篇我们学习了什么是Elasticsearch,以及Elastic stack(ELK)技术栈介绍。本篇我们来什么是正向索引和倒排索引,这是了解Elasticsearch底层架构的核心。 上一篇我们学习到,Elasticsearch的底层是由Lucene实…...

网络安全概论
一、 网络安全是一个综合性的技术。在Internet这样的环境中,其本身的目的就是为了提供一种开放式的交互环境,但是为了保护一些秘密信息,网络安全成为了在开放网络环境中必要的技术之一。网络安全技术是随着网络技术的进步逐步发展的。 网络安…...

后端开发如何高效使用 Apifox?
对于后端开发者来说,日常工作中少不了接口的设计、调试和文档编写。你是否也曾因接口文档更新不及时、测试工具分散而头疼不已?Apifox,这款全能型工具,或许能成为你的效率神器! Apifox究竟有哪些功能能帮助后端开发者…...

实现List接口的三类-ArrayList -Vector -LinkedList
一、ArrayList 数据结构与存储原理 ArrayList是基于动态数组实现的。它在内存中是一块连续的存储空间。当创建一个ArrayList时,会初始化一个默认大小(通常为10)的数组。随着元素的不断添加,如果数组容量不够,会进行扩…...

LeetCode 904.水果成篮
LeetCode 904.水果成篮 思路🧐: 求水果的最大数目,也就是求最大长度,我们是单调的向前求解,则能够想到使用滑动窗口进行解答,可以用hash表统计每个种类的个数,kinds变量统计当前种类,…...
GitHub 开源项目 Puter :云端互联操作系统
每天面对着各种云盘和在线应用,我们常常会遇到这样的困扰。 文件分散在不同平台很难统一管理,付费订阅的软件越来越多,更不用说那些烦人的存储空间限制了。 最近在 GitHub 上发现的一个开源项目 Puter 彻底改变了我的在线办公方式。 让人惊…...
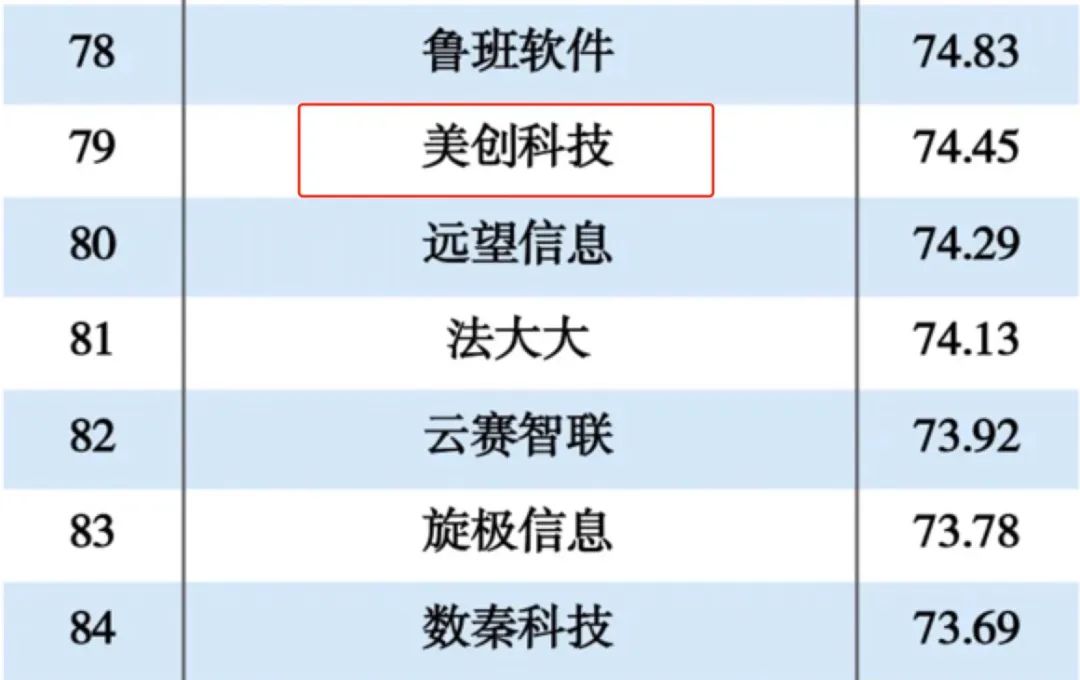
美创科技入选2024数字政府解决方案提供商TOP100!
11月19日,国内专业咨询机构DBC德本咨询发布“2024数字政府解决方案提供商TOP100”榜单。美创科技凭借在政府数据安全领域多年的项目经验、技术优势与创新能力,入选收录。 作为专业数据安全产品与服务提供商,美创科技一直致力于为政府、金融、…...

七天掌握SQL--->第五天:数据库安全与权限管理
1.1 用户权限管理 用户权限管理是指控制用户对数据库的访问和操作权限。在MySQL中,可以使用GRANT和REVOKE命令来管理用户权限。 GRANT命令用于授予用户权限。语法如下: GRANT privileges ON database.table TO userhost IDENTIFIED BY password;其中&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
