【西瓜书】剪枝与样本值处理——预剪枝、后剪枝、连续值、缺失值
目录
预剪枝
后剪枝
处理连续值
处理缺失值
剪枝(pruning)是决策树学习算法对付“过拟合”的主要手段。
- 在决策树学习过程中,有时会造成决策树分枝过多,就可能造成过拟合,可通过主动去掉一些分支来降低过离合的风险。
- 决策树剪枝的基本策略有“预剪枝”(prepruning)和“后剪枝”(postpruning)。
预剪枝
- 预剪枝是指在决策树的生成过程中,对每个节点在划分前先进行估计,若当前节点的划分不能带来决策数泛化性能提升,则停止划分,并将当前节点标记为叶节点。
- 后剪枝是先从训练集生成一颗完整的决策树,然后自底向上的对非叶节点进行考察,若将该节点对应的子树替换为叶节点,能带来决策树泛化性能提升,则将该子树替换为叶节点。
- 那么如何判断决策树的泛化性能提升呢?可以使用验证集进行验证。
- 一颗仅有一层划分的决策树,称为“决策树桩”(decision stumb)。
- 预剪枝使得决策树的很多分支都不进行展开,这既降低了过拟合的风险,又显著减少了决策树的训练时间开销和测试时间开销。
- 另一方面,有些分支的当前划分虽不能提升泛化性能,甚至可能导致泛化性能暂时下降,但是在其基础进行的后续划分却有可能导致性能显著提高。这给预剪枝决策树带来了欠拟合的风险。
- 预剪枝的本质是一种“贪心”算法。
后剪枝
- 后剪枝决策树通常比预减值决策树保留了更多的分支,一般情况下后剪纸决策树的欠拟合风险很小,泛化性能往往优于预剪纸的决策树。
- 后剪枝的训练时间开销比未剪枝决策树和预剪枝决策树都要大很多。
处理连续值
- 在处理分类时都是基于离散属性来生成决策树,使用离散值进行分类也比较符合人们的思维习惯。
- 如果输入样本的属性是连续值,就需要用到连续属性离散化的技术。
- 二分法(bi-partition)对连续属性进行处理的最简单的策略。这也是 C4.5决策树 算法中采用的机制。
- 与离散属性不同,若当前节点划分属性为连续属性,该属性还可作为其后代节点的划分属性(离散属性在决策树上只出现一次)。
处理缺失值
- 现实任务中常会遇到不完整样本,即样本的某些属性值缺失。
- 如果在属性值缺失的时候丢弃该样本,则会造成样本变得很小,因此有必要考虑利用缺失属性值的训练样例来进行学习。
- 缺失值的处理需要解决两个问题:
- 问题1:如何在属性值缺失的情况下进行划分属性选择。
- 问题2:给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分。
- 对于问题1:按照属性来,
- 令D~表示D中在属性a上没有缺失值的样本,
- 定义ρ为无缺失值的样本比例,
- 定义pk~为无缺失值样本中第k类所占的比例,
- 定义rv~为无缺失值样本中在属性a上取值为a^v的样本所占的比例;
- 则信息增益为:
- 其中
-
对于问题2:按照概率来,
-
若样本x在划分属性a上的取值已知,则将x划入与其取值对应的子节点,且样本全值在子节点中保持为
。
-
若样本x在划分属性a上的取值未知,则将x同时划入所有的子节点,且样本权值与属性值
对应的子节点中调整为
。也就是说,让同一个样本以不同的概率划入到不同的子节点中去。
-
-
C4.5算法中使用了上述解决方案。
【西瓜书】决策树-CSDN博客
相关文章:
【西瓜书】剪枝与样本值处理——预剪枝、后剪枝、连续值、缺失值
目录 预剪枝 后剪枝 处理连续值 处理缺失值 剪枝(pruning)是决策树学习算法对付“过拟合”的主要手段。 在决策树学习过程中,有时会造成决策树分枝过多,就可能造成过拟合,可通过主动去掉一些分支来降低过离合的风…...

NLP 1、人工智能与NLP简介
人人都不看好你,可偏偏你最争气 —— 24.11.26 一、AI和NLP的基本介绍 1.人工智能发展流程 弱人工智能 ——> 强人工智能 ——> 超人工智能 ① 弱人工智能 人工智能算法只能在限定领域解决特定的问题 eg:特定场景下的文本分类、垂直领域下的对…...

常见线程安全问题之Double Checked Locking
创作内容丰富的干货文章很费心力,感谢点过此文章的读者,点一个关注鼓励一下作者,激励他分享更多的精彩好文,谢谢大家! 双重锁定检查(Double Checked Locking,下称 DCL)是并发下实现懒…...
的作用 详细解读)
Redis(非关系型数据库)的作用 详细解读
edis(Remote Dictionary Server)是一个开源的、高性能的、基于内存的数据结构存储系统。它具有极高的读写性能,并且能够支持多种数据结构的存储。Redis 最初的设计目标是作为一个缓存解决方案,但随着其功能的不断扩展,…...

互联网视频推拉流EasyDSS视频直播点播平台视频转码有哪些技术特点和应用?
视频转码本质上是一个先解码再编码的过程。在转码过程中,原始视频码流首先被解码成原始图像数据,然后再根据目标编码标准、分辨率、帧率、码率等参数重新进行编码。这样,转换前后的码流可能遵循相同的视频编码标准,也可能不遵循。…...

python之多元线性回归
目录 前言实战 前言 多元线性回归是回归分析中的一种复杂模型,它考虑了多个输入变量对输出变量的影响。与一元线性回归不同,多元线性回归通过引入多个因素,更全面地建模了系统关系。 多元线性回归模型的表达式为: f ( X ) K T …...

学习threejs,使用设置lightMap光照贴图创建阴影效果
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:threejs gis工程师 文章目录 一、🍀前言1.1 ☘️THREE.MeshLambertMaterial…...

一,SQL注入解题(猫舍)
封神台 第一章:为了女神小芳! Tips: 通过sql注入拿到管理员密码! 尤里正在追女神小芳,在得知小芳开了一家公司后,尤里通过whois查询发现了小芳公司网站 学过一点黑客技术的他,想在女神面前炫炫技。于是他…...

海康大华宇视视频平台EasyCVR私有化部署视频平台海康ISUP是什么?如何接入到EasyCVR?
在现代安防领域,随着技术的发展和需求的增加,对于视频监控系统的远程管理和互联互通能力提出了更高的要求。海康威视的ISUP协议(以及功能相似的EHOME协议)因此应运而生,它们为不具备固定IP接入的设备提供了一种有效的中…...

Java ArrayList 与顺序表:在编程海洋中把握数据结构的关键之锚
我的个人主页 我的专栏:Java-数据结构,希望能帮助到大家!!!点赞❤ 收藏❤ 前言:在 Java编程的广袤世界里,数据结构犹如精巧的建筑蓝图,决定着程序在数据处理与存储时的效率、灵活性以…...
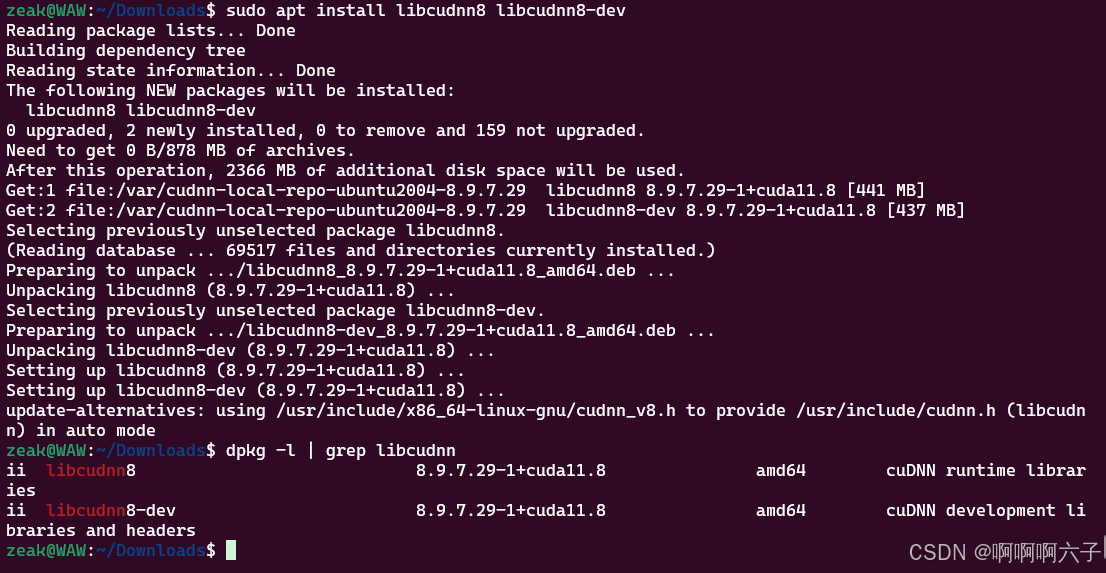
windows下安装wsl的ubuntu,同时配置深度学习环境
写在前面,本次文章只是个人学习记录,不具备教程的作用。个别信息是网上的,我会标注,个人是gpt生成的 安装wsl 直接看这个就行;可以不用备份软件源。 https://blog.csdn.net/weixin_44301630/article/details/1223900…...

开展网络安全成熟度评估:业务分析师的工具和技术
想象一下,您坐在飞机驾驶舱内。起飞前,您需要确保所有系统(从发动机到导航工具)均正常运行。现在,将您的业务视为飞机,将网络安全视为飞行前必须检查的系统。就像飞行员依赖检查表一样,业务分析师使用网络安全成熟度评估来评估组织对网络威胁的准备程度。这些评估可帮助…...

Maven Surefire 插件简介
Maven Surefire 插件是 Maven 构建系统中的一个关键组件,专门用于在构建生命周期中执行单元测试。 它通常与 Maven 构建生命周期的测试阶段绑定,确保所有单元测试在项目编译后和打包前被执行。 最新版本 Maven Surefire 插件的最新版本为 3.5.2。 使…...

基于微信小程序的平价药房管理系统+LW参考示例
1.项目介绍 系统角色:管理员、医生、普通用户功能模块:用户管理、医生管理、药品分类管理、药品信息管理、在线问诊管理、生活常识管理、日常提醒管理、过期处理、订单管理等技术选型:SpringBoot,Vue,uniapp等测试环境…...

react 前端最后阶段静态服务器启动命令
这个错误是因为你还没有安装 serve 工具。让我们一步步解决: 首先全局安装 serve: npm install -g serve如果上面的命令报错,可能是因为权限问题,可以尝试: 安装完成后,再运行: Windows 下使用…...

Flink中普通API的使用
本篇文章从Source、Transformation(转换因子)、sink这三个地方进行讲解 Source: 创建DataStream本地文件SocketKafka Transformation(转换因子): mapFlatMapFilterKeyByReduceUnion和connectSide Outpu…...

高性能 ArkUI 应用开发:复杂 UI 场景中的内存管理与 XML 优化
本文旨在深入探讨华为鸿蒙HarmonyOS Next系统(截止目前API12)的技术细节,基于实际开发实践进行总结。 主要作为技术分享与交流载体,难免错漏,欢迎各位同仁提出宝贵意见和问题,以便共同进步。 本文为原创内容,任何形式的转载必须注明出处及原作者。 在开发高性能 ArkUI 应…...

用天翼云搭建一个HivisionIDPhoto证件照处理网站
世人不必记我,我不记世人。 HivisionIDPhoto证件照处理网站 世人不必记我,我不记世人。项目地址项目搭建与修改前端后端遇到的坑 成果图 前段时间工作需要频繁处理证件照,当时同事推荐一个证件照小程序(要看广告)&…...

【算法一周目】滑动窗口(2)
目录 水果成篮 解题思路 代码实现 找到字符串中所有字母异位词 解题思路 代码实现 串联所有单词的子串 解题思路 代码实现 最小覆盖子串 解题思路 代码实现 水果成篮 题目链接:904. 水果成篮 题目描述: 你正在探访一家农场,农场…...

Zustand:一个轻量级的React状态管理库
文章目录 前言一、安装Zustand二、使用Zustand三、实际案例结语 前言 在现代Web开发中,状态管理是一个常见的需求,特别是在构建大型或复杂的单页面应用程序(SPA)时。React等框架虽然提供了基本的状态管理功能,但对于复…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
