【Java】二叉树:数据海洋中灯塔式结构探秘(上)

个人主页 🌹:喜欢做梦
二叉树中有一个树,我们可以猜到他和树有关,那我们先了解一下什么是树,在来了解一下二叉树
一🍝、树型结构
1🍨.什么是树型结构?
树是一种非线性的数据结构,它是由n(n>=0)个有限节点(结点)和边组成的层次结构的集合。有一个特定的节点为根节点,其余节点通过边连接形成的分支,每个节点可以有零个或多个子节点。把它叫做树是因为它看起来像一颗倒挂的树,也就是说它是根朝上,而叶朝下的。


什么是线性结构?什么是非线性结构?
线性结构:数据元素呈现一对一的线性关系,除第一个和最后一个元素外,每个元素都有且仅有一个直接前驱和一个直接后继;
非线性结构:数据元素之间的关系不是简单的一对一,一个元素可能有多个前驱或后继,或者两者都有。
- 树的定义是递归的;
- 除根节点外的每一个结点都能引出一颗子树;
- 树型结构中,子树之间不能有交集,否则就不是树型结构;
- 除了跟节点之外,每个节点有且只有一个父节点;
- 一个N个节点的树有N-1条边,因为根节点的上方没有边;
2🍩.什么是非树型结构?
非树:节点间的连通性复杂,可能存在多个路径连接统一对节点,也肯存在孤立节点,即与其他节点无连接。

3🍪.树型结构的基本性质

- 结点的度:一个结点含有子树的个数称为该结点的度;如上图,A的度为3,C的度为2;
- 树的度:一颗树中,所有结点度的最大值称为结点的度;如上图,树的度为4;
- 叶子结点或终端结点:度为0的节点称为叶结点;如上图,E、F、G、P等结点为叶节点;
- 孩子结点或子结点:一个结点含有子树的根结点称为该结点的子结点即只有根节点的结点才是子节点;如上图,B是A的孩子结点;
- 双亲结点或父亲结点:若一个结点含有子结点,则这个树称为该结点的父结点;如图上A是B的父节点;
- 根结点:一个树没有双亲的结点;如上图,A;
- 结点的层次:从根开始定义,根为第一层,根的子结点为第二层,一次类推;
- 树的高度或深度:树中结点的最大层次;如上图,树的高度为4;
- 以下只需了解的概念:
- 非终端结点或分支结点:除根结点外,度不为0的结点;如上图:B、C、D、H为分支节点;
- 兄弟结点:具有相同父结点的结点互称为兄弟结点;如上图:B、C是兄弟结点;
- 堂兄弟结点:不具有同一个父结点,但双亲在同一层的结点互为堂兄弟;如上图,G和H;
- 结点的祖先:从根到该结点所经分支的所有结点;如上图,A就是所有结点的祖先;
- 子孙:以某结点为根的子树中的任一节点,都称为该结点的子孙。如上图,所有结点都是A的子孙;
- 森林:有m(m>=0)课互不相交的树组成的集合称为森林;
4🍨.树的表现形式(了解)
树的表现形式有很多种,如双亲表示法,孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。这里简单了解一下其中最常见的方法就是孩子兄弟表示法:
class Node{public int value;//数据public Node firstChild;//第一个孩子public Node nextBrother;//下一个兄弟
}
二🍝、二叉树
1🍑.什么是二叉树?
二叉树:二叉树是每个结点最多有两科子树的树的结构,其两个子树通常称为左子树和右子树。
二叉树的递归定义:
- 或者是一颗空树;
- 或者是一颗由一根结点和两课互不相交的分别称为左子树和右子树所组成的非空数,左子树和右子树又同样是二叉树;

特点:
- 度的限制:结点的度最大为2;
- 有序性:左右子树由顺序,即使某节点只有一颗子树,也要区分左右子树;
性质:
- 若规定的根节点层数为1,这一棵非空二叉树的第i层上最多有
(i>.0)个节点;
- 若规定只有根节点的二叉树的深度为1,则深度为k的二叉树的最大节点数是
(k>=0);
- 对于任何一棵二叉树,如果其叶节点个数为n0,度为2的非叶节点个数为n2,则有n0=n2+1;
- 对于一颗有n个节点的m个二叉树(m表示树的度),其最小深度计算公式:
(n(m-1)+1);

2🍑.二叉树的类型
1.满二叉树
满二叉树:每一层的结点树都达到最大,除最后一层外每个节点都有两个节点。

特点:
- 节点度数:除最后一层的叶子节点外,其他层的每一个的节点都有两个节点,即度都为2;
- 叶子节点:所有的叶子节点都在同一层,且叶子节点的数量为
,k为数的高度;
- 节点总数: 节点总数是
;

2.完全二叉树
完全二叉树:除最后一层外,其余层节点数都达到最大,最后一层节点从左到右依次按顺序排列,可通过数组的高效和访问,完全二叉树是满二叉树的一种。

特点:
- 节点度数:除了底层的叶子节点外,其余所有节点都有两个子节点,即度数均为2;
- 叶子节点分布:所有叶子节点都在同一层,这使得树的结构呈现出完美的形态;
- 具有n个节点的完全二叉树的深度k为
(n+1)上取整进1;
总节点个数与叶子节点个数的关系:
- 如果总节点个数为偶数,那么叶子节点为总节点个数的一半,也就是n=2n0;
- 如果总节点个数为奇数,那么叶子节点为总节点个数的一半再减一,也就是n=2n0-1;
- 节点数量:对于具有n个节点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,这对于序号为i的节点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根节点的编号,无双亲节点;
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子;
- 若2i+1<n,右孩子序号:2i+2,否则无右孩子;

3🍪.二叉树的创建

public class BinaryTree {public static class TreeNode{public char val;//数据public TreeNode left;//左孩子public TreeNode right;//右孩子public TreeNode(char val) {this.val = val;}}public TreeNode createTree(){//创建节点TreeNode A=new TreeNode('A');TreeNode B=new TreeNode('B');TreeNode C=new TreeNode('C');TreeNode D=new TreeNode('D');TreeNode E=new TreeNode('E');TreeNode F=new TreeNode('F');TreeNode G=new TreeNode('G');//连接节点A.left=B;A.right=C;B.left=D;B.right=E;C.left=F;C.right=G;return A;}
}4.二叉树的遍历
二叉树的遍历是指按照一定的顺序访问二叉树中的每个节点,且每个节点仅被访问一次。
二叉树的遍历方式主要有前序遍历、中序遍历、后序遍历;
前序遍历
前序遍历:遍历顺序是先访问根的的节点—>左子树—>右子树,也就是根、左、右;

前序遍历代码:
// 前序遍历public void preOrder(TreeNode root){//判断是否有节点,没有返回if(root == null){return;}System.out.print(root.val+ " ");//遍历左子树preOrder(root.left);//遍历右子树preOrder(root.right);}


- 顺序:根节点--左子树--右子树;
- 根结点的打印位置:第一个;
中序遍历
中序遍历:遍历顺序是先访问左子树—>根的的节点—>右子树,也就是左、根、右;

中序遍历代码:
// 中序遍历public void inOrder(TreeNode root){//判断是否有节点,没有返回if(root == null){return;}//遍历左子树preOrder(root.left);System.out.print(root.val+ " ");//遍历右子树preOrder(root.right);}





- 顺序:左子树--根节点--右子树;
- 根结点的打印位置:中间;
后序遍历
后序遍历:遍历顺序是先访问左子树—>右子树—>根的的节点,也就是左、根、右;

// 后序遍历public void postOrder(TreeNode root){//判断是否有节点,没有返回if(root == null){return;}//遍历左子树preOrder(root.left);//遍历右子树preOrder(root.right);System.out.print(root.val+ " ");}
}后序遍历的过程与前面的也是同理,就不画图过多解释了。
- 顺序:左子树--右子树--根节点;
- 根结点的打印位置:最后一个;
三者之间的区别:
| 前序遍历 | 中序遍历 | 后序遍历 | |
| 访问顺序 | 根、左、右 | 左、根、右 | 左、右、根 |
| 根节点访问位置 | 第一个 | 中间 | 最后一个 |
| 应用场景 | 二叉树结构、将表达式树转换为前缀表达式 | 用于输出有序序列,还能辅助将表达式树转换为中缀表达式 | 二叉树的高度、节点数,以及释放二叉树内存 |
层序遍历
层序遍历:从上至下,从左至右逐层访问就是层序遍历。

层序遍历的代码,我后期补上,或者下篇在写,这篇就到这里啦~

我的博客即将同步至腾讯云开发者社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=3k88uddoizs48
相关文章:

【Java】二叉树:数据海洋中灯塔式结构探秘(上)
个人主页 🌹:喜欢做梦 二叉树中有一个树,我们可以猜到他和树有关,那我们先了解一下什么是树,在来了解一下二叉树 一🍝、树型结构 1🍨.什么是树型结构? 树是一种非线性的数据结构&…...

微信小程序 WXS 的概念与基本用法教程
微信小程序 WXS 的概念与基本用法教程 引言 在微信小程序的开发中,WXS(WeiXin Script)是一种特殊的脚本语言,旨在解决小程序在逻辑处理和数据处理上的一些限制。WXS 允许开发者在小程序的 WXML 中嵌入 JavaScript 代码,以便实现更复杂的逻辑处理。本文将深入探讨 WXS 的…...

Vue.js 中 v-bind 和 v-model 的用法与异同
简介 在 Vue.js 中,v-bind 和 v-model 是两个非常常用且强大的指令,它们分别用于动态地绑定属性和实现双向数据绑定。理解这两个指令的用法和区别对于构建 Vue.js 应用至关重要。本文将详细介绍 v-bind 和 v-model 的用法,并探讨它们的异同。…...

K8s的水平自动扩容和缩容HPA
HPA全称是Horizontal Pod Autoscaler,翻译成中文是POD水平自动伸缩,HPA可以基于CPU利用率对replication controller、deployment和replicaset中的pod数量进行自动扩缩容(除了CPU利用率也可以基于其他应程序提供的度量指标custom metrics进行自…...

【AI日记】24.11.26 聚焦 kaggle 比赛
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】【AI日记】 核心工作 1 内容:研究 kaggle 比赛时间:3 小时 核心工作 2 内容:学习 kaggle 比赛 Titanic - Machine Learning from Disaster时间:4 小时备注:这…...
大型语言模型LLM - Finetuning vs Prompting
资料来自台湾大学李宏毅教授机器学课程ML 2023 Spring,如有侵权请通知下架 台大机器学课程ML 2023 Springhttps://speech.ee.ntu.edu.tw/~hylee/ml/2023-spring.php2023/3/10 课程 機器如何生成文句 内容概要 主要探讨了大型语言模型的两种不同期待及其导致的两类…...

【IEEE独立出版 | 厦门大学主办】第四届人工智能、机器人和通信国际会议(ICAIRC 2024,12月27-29日)
第四届人工智能、机器人和通信国际会议(ICAIRC 2024) 2024 4th International Conference on Artificial Intelligence, Robotics, and Communication 重要信息 会议官网:www.icairc.net 三轮截稿时间:2024年11月30日23:59 录…...

【GPT】力量训练是什么,必要吗,有可以替代的方式吗
什么是力量训练? 力量训练是一种通过抵抗力(如重量、阻力带、自身体重等)来刺激肌肉收缩,从而提高肌肉力量、耐力和体积的运动形式。它包括以下常见形式: 自由重量训练:使用哑铃、杠铃、壶铃等。固定器械…...
【03】Selenium+Python 八种定位元素方法
操作元素,需要先查找定位到对应的元素。 查找单个元素:driver.find_element() 返回是一个web element 对象 查找多个元素:driver.find_elements() 返回是一个list对象 By 是 Selenium 中一个非常重要的类,用于定位网页元素。 使…...

笔记:jQuery追加js时会自动加“_时间戳“参数,导致百度统计失败
问题描述: $(document.createElement("script")).attr(id, baidutj).attr(src, https://hm.baidu.com/hm.js?xxx).appendTo(body); 会自动给src加_时间戳的参数? 问题解疑: 【未完待续…】 问题解决: 老老实实按它…...

【PyTorch】(基础二)---- 张量
张量 在 PyTorch 中,张量(Tensor)是核心数据结构,类似于 NumPy 中的数组,但具有更强的计算能力和对 GPU 的支持。 创建 从列表或数组创建 import torch# 从列表创建 tensor_from_list torch.tensor([1, 2, 3, 4])…...

充满智慧的埃塞俄比亚狼
非洲的青山 随着地球温度上升,贝尔山顶峰的冰川消失殆尽,许多野生动物移居到海拔3000米以上的高原上生活,其中就包括埃塞俄比亚狼。埃塞俄比亚狼是埃塞俄比亚特有的动物,总数不到500只,为“濒危”物种。 埃塞俄比亚狼…...
基于STM32设计的智能桌面暖风机(华为云IOT)
一、前言 1.1 项目开发背景 随着智能家居技术的迅猛发展,传统家用电器正逐步向智能化方向转型。暖风机作为冬季广泛使用的取暖设备,其智能化升级不仅能够提高用户的使用体验,还能通过物联网技术实现远程控制和数据监控,赋予其更…...

零基础学安全--云技术基础
目录 学习连接 前言 云技术历史 云服务 公有云服务商 云分类 基础设施即服务(IaaS) 平台即服务(PaaS) 软件即服务(SaaS) 云架构 虚拟化 容器 云架构设计 组件选择 基础设施即代码 集成部署…...

Spring Boot中配置Flink的资源管理
在 Spring Boot 中配置 Flink 的资源管理,需要遵循以下步骤: 添加 Flink 依赖项 在你的 pom.xml 文件中,添加 Flink 和 Flink-connector-kafka 的依赖项。这里以 Flink 1.14 版本为例: <!-- Flink dependencies --><de…...
51单片机从入门到精通:理论与实践指南入门篇(二)
续51单片机从入门到精通:理论与实践指南(一)https://blog.csdn.net/speaking_me/article/details/144067372 第一篇总体给大家在(全局)总体上讲解了一下51单片机,那么接下来几天结束详细讲解,从…...
Notepad++ 替换所有数字给数字加单引号
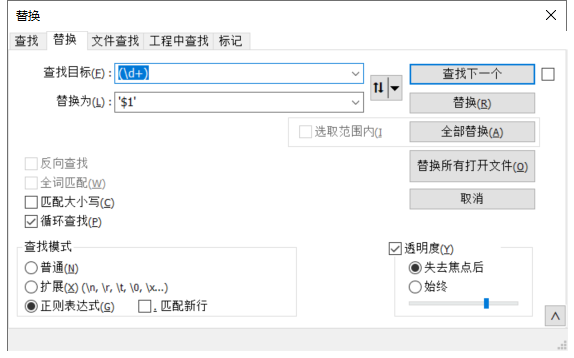
前言 今天遇到这样一个场景: 要去更新某张表里 code1,2,3,4,5,6 的数据,把它的 name 设置为 ‘张三’ 但是 code在数据库里面的字段类型是 vachar(64),它自身携带索引 原本可以这样写 SQL: update tableA set namezhangsan where code in …...

【CANOE】【Capl】【RS232】控制串口设备
系列文章目录 内置函数,来控制传统的串口设备,比如继电器等 文章目录 系列文章目录前言一、控制串口二、自定义相关的参数RS232Configure**函数语法****函数功能****参数说明****返回值****示例代码** 三、回调函数的使用RS232OnSend**函数语法****函数…...

查找相关题目
1.顺序查找法适合于存储结构为(B )的线性表。 A.散列存储 B.顺序存储或链式存储 C.压缩存储 D.索引存储 顺序查找法的特点 2.适用于折半查找的表的存储方式及元素排列要求为(D ) 。 A.链接方式存储,元素无序 B.链接方式存储࿰…...
《独立开发:Spring 框架的综合应用》
一、Spring 框架概述 Spring 是一个分层的 Java SE/EE full-stack 轻量级开源框架,以 IoC 和 AOP 为内核,具有方便解耦、方便集成优秀框架、降低 Java EE API 使用难度等优点。 Spring 框架因其强大的功能以及卓越的性能而受到众多开发人员的喜爱。它是…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
