【深度学习基础】预备知识 | 微积分

【作者主页】Francek Chen
【专栏介绍】 ⌈ ⌈ ⌈PyTorch深度学习 ⌋ ⌋ ⌋ 深度学习 (DL, Deep Learning) 特指基于深层神经网络模型和方法的机器学习。它是在统计机器学习、人工神经网络等算法模型基础上,结合当代大数据和大算力的发展而发展出来的。深度学习最重要的技术特征是具有自动提取特征的能力。神经网络算法、算力和数据是开展深度学习的三要素。深度学习在计算机视觉、自然语言处理、多模态数据分析、科学探索等领域都取得了很多成果。本专栏介绍基于PyTorch的深度学习算法实现。
【GitCode】专栏资源保存在我的GitCode仓库:https://gitcode.com/Morse_Chen/PyTorch_deep_learning。
文章目录
- 一、导数和微分
- 二、偏导数
- 三、梯度
- 四、链式法则
- 小结
在2500年前,古希腊人把一个多边形分成三角形,并把它们的面积相加,才找到计算多边形面积的方法。为了求出曲线形状(比如圆)的面积,古希腊人在这样的形状上刻内接多边形。如图1所示,内接多边形的等长边越多,就越接近圆。这个过程也被称为逼近法(method of exhaustion)。

事实上,逼近法就是积分(integral calculus)的起源。2000多年后,微积分的另一支,微分(differential calculus)被发明出来。在微分学最重要的应用是优化问题,即考虑如何把事情做到最好。正如在【深度学习基础】深度学习导论 中讨论的那样,这种问题在深度学习中是无处不在的。
在深度学习中,我们“训练”模型,不断更新它们,使它们在看到越来越多的数据时变得越来越好。通常情况下,变得更好意味着最小化一个损失函数(loss function),即一个衡量“模型有多糟糕”这个问题的分数。最终,我们真正关心的是生成一个模型,它能够在从未见过的数据上表现良好。但“训练”模型只能将模型与我们实际能看到的数据相拟合。因此,我们可以将拟合模型的任务分解为两个关键问题:
- 优化(optimization):用模型拟合观测数据的过程;
- 泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型。
为了帮助读者在后面的章节中更好地理解优化问题和方法,本节提供了一个非常简短的入门教程,帮助读者快速掌握深度学习中常用的微分知识。
一、导数和微分
我们首先讨论导数的计算,这是几乎所有深度学习优化算法的关键步骤。在深度学习中,我们通常选择对于模型参数可微的损失函数。简而言之,对于每个参数,如果我们把这个参数增加或减少一个无穷小的量,可以知道损失会以多快的速度增加或减少。
假设我们有一个函数 f : R → R f: \mathbb{R} \rightarrow \mathbb{R} f:R→R,其输入和输出都是标量。如果 f f f的导数存在,这个极限被定义为
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h (1) f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}\tag{1} f′(x)=h→0limhf(x+h)−f(x)(1)
如果 f ′ ( a ) f'(a) f′(a)存在,则称 f f f在 a a a处是可微(differentiable)的。如果 f f f在一个区间内的每个数上都是可微的,则此函数在此区间中是可微的。我们可以将式(1)中的导数 f ′ ( x ) f'(x) f′(x)解释为 f ( x ) f(x) f(x)相对于 x x x的瞬时(instantaneous)变化率。所谓的瞬时变化率是基于 x x x中的变化 h h h,且 h h h接近 0 0 0。
为了更好地解释导数,让我们做一个实验。定义 u = f ( x ) = 3 x 2 − 4 x u=f(x)=3x^2-4x u=f(x)=3x2−4x 如下:
%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2ldef f(x):return 3 * x ** 2 - 4 * x
通过令 x = 1 x=1 x=1并让 h h h接近 0 0 0,式(1)中 f ( x + h ) − f ( x ) h \frac{f(x+h)-f(x)}{h} hf(x+h)−f(x)的数值结果接近 2 2 2。虽然这个实验不是一个数学证明,但稍后会看到,当 x = 1 x=1 x=1时,导数 u ′ u' u′是 2 2 2。
def numerical_lim(f, x, h):return (f(x + h) - f(x)) / hh = 0.1
for i in range(5):print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')h *= 0.1

让我们熟悉一下导数的几个等价符号。给定 y = f ( x ) y=f(x) y=f(x),其中 x x x和 y y y分别是函数 f f f的自变量和因变量。以下表达式是等价的:
f ′ ( x ) = y ′ = d y d x = d f d x = d d x f ( x ) = D f ( x ) = D x f ( x ) f'(x) = y' = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx} f(x) = Df(x) = D_x f(x) f′(x)=y′=dxdy=dxdf=dxdf(x)=Df(x)=Dxf(x) 其中符号 d d x \frac{d}{dx} dxd和 D D D是微分运算符,表示微分操作。我们可以使用以下规则来对常见函数求微分:
- D C = 0 DC = 0 DC=0( C C C是一个常数)
- D x n = n x n − 1 Dx^n = nx^{n-1} Dxn=nxn−1(幂律(power rule), n n n是任意实数)
- D e x = e x De^x = e^x Dex=ex
- D ln ( x ) = 1 / x D\ln(x) = 1/x Dln(x)=1/x
为了微分一个由一些常见函数组成的函数,下面的一些法则方便使用。假设函数 f f f和 g g g都是可微的, C C C是一个常数,则:
常数相乘法则
d d x [ C f ( x ) ] = C d d x f ( x ) , (2) \frac{d}{dx} [Cf(x)] = C \frac{d}{dx} f(x),\tag{2} dxd[Cf(x)]=Cdxdf(x),(2)
加法法则
d d x [ f ( x ) + g ( x ) ] = d d x f ( x ) + d d x g ( x ) , (3) \frac{d}{dx} [f(x) + g(x)] = \frac{d}{dx} f(x) + \frac{d}{dx} g(x),\tag{3} dxd[f(x)+g(x)]=dxdf(x)+dxdg(x),(3)
乘法法则
d d x [ f ( x ) g ( x ) ] = f ( x ) d d x [ g ( x ) ] + g ( x ) d d x [ f ( x ) ] , (4) \frac{d}{dx} [f(x)g(x)] = f(x) \frac{d}{dx} [g(x)] + g(x) \frac{d}{dx} [f(x)],\tag{4} dxd[f(x)g(x)]=f(x)dxd[g(x)]+g(x)dxd[f(x)],(4)
除法法则
d d x [ f ( x ) g ( x ) ] = g ( x ) d d x [ f ( x ) ] − f ( x ) d d x [ g ( x ) ] [ g ( x ) ] 2 . (5) \frac{d}{dx} \left[\frac{f(x)}{g(x)}\right] = \frac{g(x) \frac{d}{dx} [f(x)] - f(x) \frac{d}{dx} [g(x)]}{[g(x)]^2}.\tag{5} dxd[g(x)f(x)]=[g(x)]2g(x)dxd[f(x)]−f(x)dxd[g(x)].(5)
现在我们可以应用上述几个法则来计算 u ′ = f ′ ( x ) = 3 d d x x 2 − 4 d d x x = 6 x − 4 u'=f'(x)=3\frac{d}{dx}x^2-4\frac{d}{dx}x=6x-4 u′=f′(x)=3dxdx2−4dxdx=6x−4。令 x = 1 x=1 x=1,我们有 u ′ = 2 u'=2 u′=2:在这个实验中,数值结果接近 2 2 2,这一点得到了在本节前面的实验的支持。当 x = 1 x=1 x=1时,此导数也是曲线 u = f ( x ) u=f(x) u=f(x)切线的斜率。
为了对导数的这种解释进行可视化,我们将使用matplotlib,这是一个Python中流行的绘图库。要配置matplotlib生成图形的属性,我们需要定义几个函数。在下面,use_svg_display函数指定matplotlib软件包输出svg图表以获得更清晰的图像。
注意,注释#@save是一个特殊的标记,会将对应的函数、类或语句保存在d2l包中。因此,以后无须重新定义就可以直接调用它们(例如,d2l.use_svg_display())。
def use_svg_display(): #@save"""使用svg格式在Jupyter中显示绘图"""backend_inline.set_matplotlib_formats('svg')
我们定义set_figsize函数来设置图表大小。注意,这里可以直接使用d2l.plt,因为导入语句from matplotlib import pyplot as plt已标记为保存到d2l包中。
def set_figsize(figsize=(3.5, 2.5)): #@save"""设置matplotlib的图表大小"""use_svg_display()d2l.plt.rcParams['figure.figsize'] = figsize
下面的set_axes函数用于设置由matplotlib生成图表的轴的属性。
#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):"""设置matplotlib的轴"""axes.set_xlabel(xlabel)axes.set_ylabel(ylabel)axes.set_xscale(xscale)axes.set_yscale(yscale)axes.set_xlim(xlim)axes.set_ylim(ylim)if legend:axes.legend(legend)axes.grid()
通过这三个用于图形配置的函数,定义一个plot函数来简洁地绘制多条曲线,因为我们需要在整个书中可视化许多曲线。
#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,ylim=None, xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):"""绘制数据点"""if legend is None:legend = []set_figsize(figsize)axes = axes if axes else d2l.plt.gca()# 如果X有一个轴,输出Truedef has_one_axis(X):return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)and not hasattr(X[0], "__len__"))if has_one_axis(X):X = [X]if Y is None:X, Y = [[]] * len(X), Xelif has_one_axis(Y):Y = [Y]if len(X) != len(Y):X = X * len(Y)axes.cla()for x, y, fmt in zip(X, Y, fmts):if len(x):axes.plot(x, y, fmt)else:axes.plot(y, fmt)set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
现在我们可以绘制函数 u = f ( x ) u=f(x) u=f(x)及其在 x = 1 x=1 x=1处的切线 y = 2 x − 3 y=2x-3 y=2x−3,其中系数 2 2 2是切线的斜率。
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

二、偏导数
到目前为止,我们只讨论了仅含一个变量的函数的微分。在深度学习中,函数通常依赖于许多变量。因此,我们需要将微分的思想推广到多元函数(multivariate function)上。
设 y = f ( x 1 , x 2 , … , x n ) y = f(x_1, x_2, \ldots, x_n) y=f(x1,x2,…,xn)是一个具有 n n n个变量的函数。 y y y关于第 i i i个参数 x i x_i xi的偏导数(partial derivative)为:
∂ y ∂ x i = lim h → 0 f ( x 1 , … , x i − 1 , x i + h , x i + 1 , … , x n ) − f ( x 1 , … , x i , … , x n ) h (6) \frac{\partial y}{\partial x_i} = \lim_{h \rightarrow 0} \frac{f(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots, x_n) - f(x_1, \ldots, x_i, \ldots, x_n)}{h}\tag{6} ∂xi∂y=h→0limhf(x1,…,xi−1,xi+h,xi+1,…,xn)−f(x1,…,xi,…,xn)(6)
为了计算 ∂ y ∂ x i \frac{\partial y}{\partial x_i} ∂xi∂y,我们可以简单地将 x 1 , … , x i − 1 , x i + 1 , … , x n x_1, \ldots, x_{i-1}, x_{i+1}, \ldots, x_n x1,…,xi−1,xi+1,…,xn看作常数,并计算 y y y关于 x i x_i xi的导数。对于偏导数的表示,以下是等价的:
∂ y ∂ x i = ∂ f ∂ x i = f x i = f i = D i f = D x i f (7) \frac{\partial y}{\partial x_i} = \frac{\partial f}{\partial x_i} = f_{x_i} = f_i = D_i f = D_{x_i} f\tag{7} ∂xi∂y=∂xi∂f=fxi=fi=Dif=Dxif(7)
三、梯度
我们可以连结一个多元函数对其所有变量的偏导数,以得到该函数的梯度(gradient)向量。具体而言,设函数 f : R n → R f:\mathbb{R}^n\rightarrow\mathbb{R} f:Rn→R的输入是一个 n n n维向量 x = [ x 1 , x 2 , … , x n ] ⊤ \mathbf{x}=[x_1,x_2,\ldots,x_n]^\top x=[x1,x2,…,xn]⊤,并且输出是一个标量。函数 f ( x ) f(\mathbf{x}) f(x)相对于 x \mathbf{x} x的梯度是一个包含 n n n个偏导数的向量:
∇ x f ( x ) = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , … , ∂ f ( x ) ∂ x n ] ⊤ (8) \nabla_{\mathbf{x}} f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_n}\bigg]^\top\tag{8} ∇xf(x)=[∂x1∂f(x),∂x2∂f(x),…,∂xn∂f(x)]⊤(8) 其中 ∇ x f ( x ) \nabla_{\mathbf{x}} f(\mathbf{x}) ∇xf(x)通常在没有歧义时被 ∇ f ( x ) \nabla f(\mathbf{x}) ∇f(x)取代。
假设 x \mathbf{x} x为 n n n维向量,在微分多元函数时经常使用以下规则:
- 对于所有 A ∈ R m × n \mathbf{A} \in \mathbb{R}^{m \times n} A∈Rm×n,都有 ∇ x A x = A ⊤ \nabla_{\mathbf{x}} \mathbf{A} \mathbf{x} = \mathbf{A}^\top ∇xAx=A⊤
- 对于所有 A ∈ R n × m \mathbf{A} \in \mathbb{R}^{n \times m} A∈Rn×m,都有 ∇ x x ⊤ A = A \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A} = \mathbf{A} ∇xx⊤A=A
- 对于所有 A ∈ R n × n \mathbf{A} \in \mathbb{R}^{n \times n} A∈Rn×n,都有 ∇ x x ⊤ A x = ( A + A ⊤ ) x \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A} \mathbf{x} = (\mathbf{A} + \mathbf{A}^\top)\mathbf{x} ∇xx⊤Ax=(A+A⊤)x
- ∇ x ∥ x ∥ 2 = ∇ x x ⊤ x = 2 x \nabla_{\mathbf{x}} \|\mathbf{x} \|^2 = \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{x} = 2\mathbf{x} ∇x∥x∥2=∇xx⊤x=2x
同样,对于任何矩阵 X \mathbf{X} X,都有 ∇ X ∥ X ∥ F 2 = 2 X \nabla_{\mathbf{X}} \|\mathbf{X} \|_F^2 = 2\mathbf{X} ∇X∥X∥F2=2X。正如我们之后将看到的,梯度对于设计深度学习中的优化算法有很大用处。
四、链式法则
然而,上面方法可能很难找到梯度。这是因为在深度学习中,多元函数通常是复合(composite)的,所以难以应用上述任何规则来微分这些函数。幸运的是,链式法则可以被用来微分复合函数。
让我们先考虑单变量函数。假设函数 y = f ( u ) y=f(u) y=f(u)和 u = g ( x ) u=g(x) u=g(x)都是可微的,根据链式法则:
d y d x = d y d u d u d x (9) \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}\tag{9} dxdy=dudydxdu(9) 现在考虑一个更一般的场景,即函数具有任意数量的变量的情况。假设可微分函数 y y y有变量 u 1 , u 2 , … , u m u_1, u_2, \ldots, u_m u1,u2,…,um,其中每个可微分函数 u i u_i ui都有变量 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn。注意, y y y是 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn的函数。对于任意 i = 1 , 2 , … , n i = 1, 2, \ldots, n i=1,2,…,n,链式法则给出:
∂ y ∂ x i = ∂ y ∂ u 1 ∂ u 1 ∂ x i + ∂ y ∂ u 2 ∂ u 2 ∂ x i + ⋯ + ∂ y ∂ u m ∂ u m ∂ x i (10) \frac{\partial y}{\partial x_i} = \frac{\partial y}{\partial u_1} \frac{\partial u_1}{\partial x_i} + \frac{\partial y}{\partial u_2} \frac{\partial u_2}{\partial x_i} + \cdots + \frac{\partial y}{\partial u_m} \frac{\partial u_m}{\partial x_i}\tag{10} ∂xi∂y=∂u1∂y∂xi∂u1+∂u2∂y∂xi∂u2+⋯+∂um∂y∂xi∂um(10)
小结
- 微分和积分是微积分的两个分支,前者可以应用于深度学习中的优化问题。
- 导数可以被解释为函数相对于其变量的瞬时变化率,它也是函数曲线的切线的斜率。
- 梯度是一个向量,其分量是多变量函数相对于其所有变量的偏导数。
- 链式法则可以用来微分复合函数。
相关文章:

【深度学习基础】预备知识 | 微积分
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈PyTorch深度学习 ⌋ ⌋ ⌋ 深度学习 (DL, Deep Learning) 特指基于深层神经网络模型和方法的机器学习。它是在统计机器学习、人工神经网络等算法模型基础上,结合当代大数据和大算力的发展而发展出来的。深度学习最重…...
)
CTF-PWN glibc源码阅读[1]: 寻找libc中堆结构的定义(2.31-0ubuntu9.16)
源代码在这里下载 来到malloc/malloc.c 在980行发现这段代码 // 定义最大 mmap 值为 -4 #define M_MMAP_MAX -4// 如果没有定义 DEFAULT_MMAP_MAX,则将其定义为 65536 #ifndef DEFAULT_MMAP_MAX #define DEFAULT_MMAP_MAX (65536) #endif// 引…...

宏集eXware物联网网关在水务管理系统上的应用
一、前言 水务管理系统涵盖了对城市水网、供水、排水、污水处理等多个环节的监控与管理。随着物联网(IoT)技术的快速发展,物联网网关逐渐成为水务管理系统中的关键组成部分。 宏集物联网网关以其高效的数据采集、传输和管理功能,…...

【大数据学习 | Spark-SQL】定义UDF和DUAF,UDTF函数
1. UDF函数(用户自定义函数) 一般指的是用户自己定义的单行函数。一进一出,函数接受的是一行中的一个或者多个字段值,返回一个值。比如MySQL中的,日期相关的dateDiff函数,字符串相关的substring函数。 先…...

#Java-JDK7、8的时间相关类,包装类
1. JDK7-Date类 我们先来看时间的相关知识点 世界标准时间: 格林尼治时间/格林威治时间(Greenwich Mean Time)简称GMT。目前世界标准时间(UTC)已经替换为:原子钟中国标准时间: 世界标准时间8小时 时间单位换算: 1秒1000毫秒 1毫秒1000微秒 1微秒1000纳秒 Date类 Date类…...

tc 命令
Windows Network Shaper目前只能在win10及以下版本使用,在github上有源码。 iperf 是一个网络性能测试工具,可以测试网络带宽和延迟。 webrtc M96版本的GCC sudo tc qdisc del dev eth1 root //关闭限速 sudo tc qdisc add dev eth1 root handle 1: ht…...
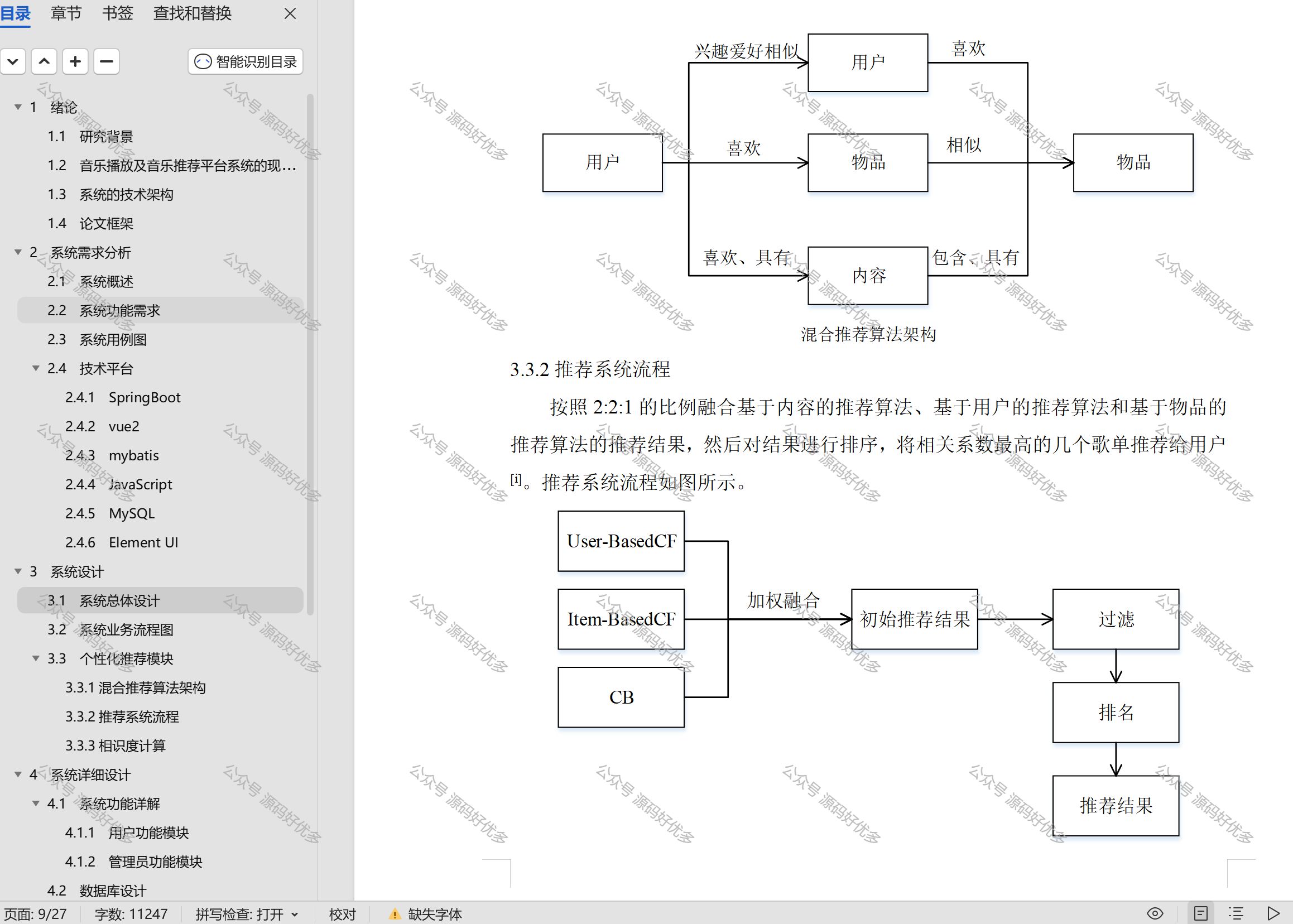
基于Java Springboot 协同过滤算法音乐推荐系统
一、作品包含 源码数据库设计文档万字全套环境和工具资源部署教程 二、项目技术 前端技术:Html、Css、Js、Vue2、Element-ui 数据库:MySQL 后端技术:Java、Spring Boot、MyBatis 三、运行环境 开发工具:IDEA 数据库&#x…...

MyBatis框架-关联映射
MyBatis关联映射-一对一 1.1 实体关系 实体–数据实体,实体关系指的就是数据与数据之间的关系 例如:订单和商品,用户和角色 实体关系分为以下四种: **一对一关联:**用户表和用户详情表 数据表关系: 主键关…...

Web开发技术栈选择指南
互联网时代的蓬勃发展,让越来越多人投身软件开发领域。面对前端和后端的选择,很多初学者往往陷入迷茫。让我们一起深入了解这两个领域的特点,帮助你做出最适合自己的选择。 在互联网发展的早期,前端开发主要负责页面布局和简单的…...

工具类的魔力:深入理解 Java 的 String、Math 和 Arrays
Java 提供了许多实用的工具类,帮助开发者简化代码,提升效率。这些工具类包含了各种常见的操作,比如字符串处理、数学计算、数组操作等。掌握这些工具类的高效使用方法,不仅能让你写出更简洁、优雅的代码,还能在性能上有…...

Linux下一次性关闭多个同名进程
要一次性关闭多个同名的 Python 进程,例如: 你可以使用以下几种方法。在执行这些操作之前,请务必确认这些进程确实是你希望终止的,以避免意外关闭其他重要的进程。 方法一:使用 pkill 命令 pkill 是一个用于根据名称…...

记录一些虚拟机桥接网络,windows网络遇到的小问题
1 virtual box 桥接的虚拟系统无 ipv4 地址 https://blog.csdn.net/qq_44847649/article/details/122582954 原因是 wlan 无线网卡没开共享给 virtual box host only (之前用过 vmware 也类似) 2 无法两台 windows10 物理机无法相互 ping 通 https://blog.csdn.net/qq_35…...

MATLAB —— 机械臂工作空间,可达性分析
系列文章目录 前言 本示例展示了如何使用可操作性指数对不同类型的机械手进行工作空间分析。工作空间分析是一种有用的工具,可用于确定机器人工作空间中最容易改变末端效应器位置和方向的区域。本示例的重点是利用不同的可操控性指数类型来分析各种机械手的工作空间。了解工作…...

18:(标准库)DMA二:DMA+串口收发数据
DMA串口收发数据 1、DMA串口发送数据2、DMA中断串口接收定长数据包3、串口空闲中断DMA接收不定长数据包4、串口空闲中断DMA接收不定长数据包DMA发送数据包 1、DMA串口发送数据 当串口的波特率大于115200时,可以通过DMA1进行数据搬运,以防止数据的丢失。如…...

【C++】 算术操作符与数据类型溢出详解
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯C 算术操作符详解基本算术操作符整数除法与取模行为类型转换在算术运算中的作用自增与自减操作符 💯数值溢出:当值超出类型范围时数据类型的取值范围…...

柔性芯片:实现万物互联的催化剂
物联网 (IoT) 市场已经非常成熟,麦肯锡预测,物联网将再创高峰,到 2030 年将达到 12.5 万亿美元的估值。然而,万物互联 (IoE) 的愿景尚未实现,即由数十亿台智能互联设备组成,提供大规模洞察和效率。 究竟是…...

FFmpeg 简介与编译
1. ffmpeg 简介: FFmpeg是一套可以用来记录、转换数字音频、视频,并能将其转化为流的开源计算机程序。采用LGPL或GPL许可证。它提供了录制、转换以及流化音视频的完整解决方案。它包含了非常先进的音频/视频编解码库libavcodec,为了保证高可移…...

低代码与微服务融合在医疗集团中的补充应用探究
摘要 本论文深入探讨了低代码与微服务融合在医疗系统集群中的应用。分析了其优势,包括提高开发效率、降低技术门槛、灵活适应需求变化和易于维护扩展等;阐述了面临的挑战,如数据安全与隐私保护、技术应用复杂性等;并展望了其在医…...

速盾:高防cdn的搜索引擎回源是什么?
高防CDN(Content Delivery Network)是一种用于加速网站访问速度和增加安全性的服务,它通过将静态和动态内容缓存在全球分布的服务器上,从而将用户请求的响应时间降至最低,并提供有效的防御攻击的能力。在实际使用过程中…...

减少电路和配电系统谐波的五种方法
K 级变压器 ANSI 标准 C57.110-1986 定义了 K 系数来评估电路消耗多少谐波电流并确定该谐波电流的热效应。根据电路 K 系数,变压器按 K 等级制造。值得注意的是,K 级变压器不会减少谐波。K 等级表示变压器承受谐波有害影响的相对能力。K级变压器增加了铁…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
