【UE5 C++】判断两点连线是否穿过球体
目录
前言
方法一
原理
代码
测试
结果
方法二
原理
一、检查连线与球体的相交情况
二、检查距离与球体半径的关系
三、检查连线与球体的相交
代码
前言
通过数学原理判断空间中任意两点的连线是否穿过球体,再通过射线检测检验算法的正确性。
方法一
原理
(1)设球体球心的坐标为 ,半径为r;
(2)设线段中A点的坐标为
,B点的坐标为
(3)计算、
、
(4)计算点到 线段
的最短距离
(5) 如果,则线段
穿过球体;如果
,则线段
不穿过球体。
代码
定义一个函数“IsCrossSphere”来判断线段是否穿过球体,函数需要传入点A、B的坐标以及球心坐标和球体半径。

再定义一个结构体作为函数返回值

函数“IsCrossSphere”的实现如下

头文件:
// Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h"
#include "GameFramework/Actor.h"
#include "LineIsCrossSphere.generated.h"USTRUCT(BlueprintType)
struct FStruct_Result_IsLineCrossSphere
{GENERATED_BODY();
public:UPROPERTY(BlueprintReadWrite)float distanceOfLineAndSphereCenter;UPROPERTY(BlueprintReadWrite)bool isCrossSphere;
};UCLASS()
class STUDY_API ALineIsCrossSphere : public AActor
{GENERATED_BODY()public: // Sets default values for this actor's propertiesALineIsCrossSphere();protected:// Called when the game starts or when spawnedvirtual void BeginPlay() override;UFUNCTION(BlueprintCallable)FStruct_Result_IsLineCrossSphere IsCrossSphere(FVector pointA, FVector pointB, FVector sphereOrginPoint, float sphereRadius); //计算线段AB到球心的距离并判断AB是否穿过球体public: // Called every framevirtual void Tick(float DeltaTime) override;};源文件:
// Fill out your copyright notice in the Description page of Project Settings.#include "Test/LineIsCrossSphere.h"// Sets default values
ALineIsCrossSphere::ALineIsCrossSphere()
{// Set this actor to call Tick() every frame. You can turn this off to improve performance if you don't need it.PrimaryActorTick.bCanEverTick = true;}// Called when the game starts or when spawned
void ALineIsCrossSphere::BeginPlay()
{Super::BeginPlay();}FStruct_Result_IsLineCrossSphere ALineIsCrossSphere::IsCrossSphere(FVector pointA, FVector pointB, FVector sphereOrginPoint, float sphereRadius)
{bool isCrossSphere;FVector OA = pointA - sphereOrginPoint;FVector OB = pointB - sphereOrginPoint;FVector AB = OB - OA;FVector n = OA.Cross(AB);float D = n.Size() / AB.Size();if (D > sphereRadius){isCrossSphere = false;}else{isCrossSphere = true;}FStruct_Result_IsLineCrossSphere result;result.isCrossSphere = isCrossSphere;result.distanceOfLineAndSphereCenter = D;return result;
}// Called every frame
void ALineIsCrossSphere::Tick(float DeltaTime)
{Super::Tick(DeltaTime);}测试
在Tick中每帧去发射射线检测并调用函数 “IsCrossSphere”,通过观察射线碰撞结果以及函数 “IsCrossSphere”的打印是否相等来判断算法是否有误。(这里设置球体半径固定为50,球体坐标为(0,0,0))

结果
可以看到不论是线段在球体表面,穿过球体,还是在球体外,函数 “IsCrossSphere”与射线检测的结果都是一致的。



方法二
原理
一、检查连线与球体的相交情况
使用距离公式计算点 到球体中心
的距离
,以及点
到地球中心
的距离
,设点
为
,点
为
。
二、检查距离与球体半径的关系
如果 且
,则两点都在球体内部,它们的连线显然穿过球体;
如果 且
,则两点都在球体外部,需要进一步检查它们的连线是否与球体相交。
三、检查连线与球体的相交
当两点都在球体外部时,我们可以计算直线 AB 的参数方程,并尝试找到与球体表面(即半径为 R 的球体)的交点。将直线的参数方程代入球体的方程,并解出一个关于参数的二次方程。如果这个二次方程有实数解,并且解对应的参数值在 0 和 1 之间(对于参数化的线段 AB),则连线与球体相交。
(1)表示直线参数方程
对于线段的参数方程可以表示为
其中是参数,
表示线段
上的点
(2)表示球体方程
设球体球心的坐标为 ,半径为
,则球体方程可表示为
(3)将直线的参数方程代入球体的方程中,得到一个关于的二次方程
![]()
展开并整理后,可得到一个标准的二次方程形式:
(4)使用求根公式可以得到二次方程的解
(5)如果二次方程没有实数解(),则直线不与球体相交;
如果二次方程有一个实数解,并且解在 0≤t≤1 的范围内,则线段 AB 与球体相交于一点;
如果二次方程有两个不同的实数解,并且至少有一个解在 0≤t≤1 的范围内,则直线段 AB 与球体相交于两点(即线段穿过球体)。
代码
bool ALineIsCrossSphere::IsCrossSphere2(FVector pointA, FVector pointB, FVector sphereOrginPoint, float sphereRadius)
{float D_A = sqrt(pow(pointA.X - sphereOrginPoint.X, 2) + pow(pointA.Y - sphereOrginPoint.Y, 2) + pow(pointA.Z - sphereOrginPoint.Z, 2)); //计算点A到球体中心的距离float D_B = sqrt(pow(pointB.X - sphereOrginPoint.X, 2) + pow(pointB.Y - sphereOrginPoint.Y, 2) + pow(pointB.Z - sphereOrginPoint.Z, 2)); //计算点B到球体中心的距离if (D_A <= sphereRadius && D_B <= sphereRadius) //两点都在球体内部,它们的连线显然穿过球体{return true;}else if (D_A > sphereRadius && D_B > sphereRadius) //两点都在球体外部{//将直线的参数方程代入球体的方程,得到标准二次方程的a、b、cfloat a = pow(pointB.X - pointA.X, 2) + pow(pointB.Y - pointA.Y, 2) + pow(pointB.Z - pointA.Z, 2);float b = 2 * ((pointB.X - pointA.X) * (pointA.X - sphereOrginPoint.X) + (pointB.Y - pointA.Y) * (pointA.Y - sphereOrginPoint.Y) + (pointB.Z - pointA.Z) * (pointA.Z - sphereOrginPoint.Z));float c = pow(pointA.X - sphereOrginPoint.X, 2) + pow(pointA.Y - sphereOrginPoint.Y, 2) + pow(pointA.Z - sphereOrginPoint.Z, 2) - pow(sphereRadius, 2);float discriminant = b * b - 4 * a * c;if (discriminant > 0.0f) //△>0{// 有两个不同的实数解float t1 = (-1*b + sqrt(pow(b, 2) - 4 * a * c)) / (2 * a);float t2 = (-1*b - sqrt(pow(b, 2) - 4 * a * c)) / (2 * a);if ((0 <= t1 && t1 <= 1) || (0 <= t2 && t2 <= 1)){return true; //至少有一个解在0~1,则线段 AB 与球体相交于两点}else {return false; //直线与球体在无限远处相交,即线段没有穿过球体}}else if (discriminant == 0.0f) //△=0{// 有两个相等的实数解(或说是一个重根)float t = (-1 * b) / (2 * a);if (t >= 0 && t <= 1){return true; //直线段 AB 与球体相交于一点}else{return false; //虽然直线在无限延伸的情况下会与球体相交,但交点并不在连接点A和点B的线段上,因此没有相交}}else //△<0{// 没有实数解,直线不与球体相交return false;}}else //一点在球体内部,另一点在球体外部,则它们的连线一定穿过球体{return true;}
}相关文章:
【UE5 C++】判断两点连线是否穿过球体
目录 前言 方法一 原理 代码 测试 结果 方法二 原理 一、检查连线与球体的相交情况 二、检查距离与球体半径的关系 三、检查连线与球体的相交 代码 前言 通过数学原理判断空间中任意两点的连线是否穿过球体,再通过射线检测检验算法的正确性。 方法一 …...

【Blender】如何创建空心管道
步骤 1:创建一个圆柱体 添加圆柱体: 在 Object Mode 下按 Shift A > Mesh > Cylinder。 步骤 2:制作空心效果 进入编辑模式: 选中圆柱体,按 Tab 进入 Edit Mode。 删除顶部和底部面: 按 3 进入面选…...

ChromeBook11 HP G7EE 刷入Ubuntu的记录
设置开发模式-> 拆电池(解锁)-> 刷入bios ->使用u盘刷入系统。 下面是详细过程,除了拆机有点紧,没有难度(我不负责~ 其实我试了好几次其他系统的,先进了pe,pe没问题(音频x),有一个win10的u盘(几个…...

16asm - 汇编介绍 和 debug使用
文章目录 前言硬件运行机制微机系统硬件组成计算机系统组成8086cpu组织架构dosbox安装配置debug debug使用R命令D命令E命令U命令T命令A命令标志寄存器 总结 前言 各位师傅大家好,我是qmx_07,今天给大家讲解 十六位汇编 和 debug调试器的使用 硬件运行…...
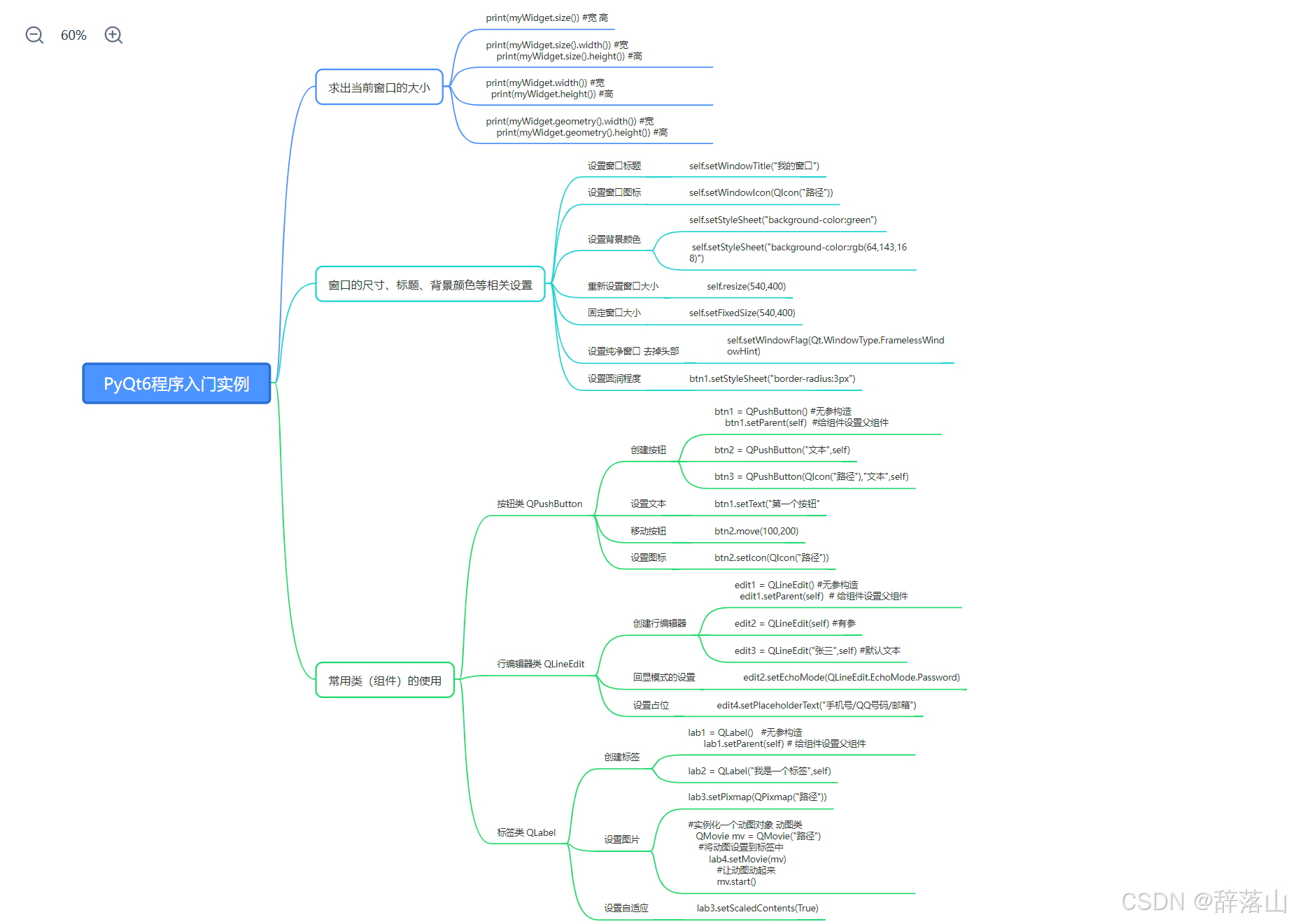
初识QT第一天
思维导图 利用Qt尝试做出原神登陆界面 import sys from PyQt6.QtGui import QIcon, QPixmap, QMovie from PyQt6.QtWidgets import QApplication, QWidget, QLabel, QPushButton, QLineEdit# 封装原神窗口类 class Genshin(QWidget):# 构造函数def __init__(self):# 初始化父类…...

ChatGPT科研应用、论文写作、课题申报、数据分析与AI绘图
随着人工智能技术的飞速发展,ChatGPT等先进语言模型正深刻改变着科研工作的面貌。从科研灵感的激发、论文的高效撰写,到课题的成功申报,乃至复杂数据的深度分析与可视化呈现,AI技术均展现出前所未有的潜力。其实众多科研前沿工作者…...

原子类、AtomicLong、AtomicReference、AtomicIntegerFieldUpdater、LongAdder
原子类 JDK提供的原子类,即Atomic*类有很多,大体可做如下分类: 形式类别举例Atomic*基本类型原子类AtomicInteger、AtomicLong、AtomicBooleanAtomic*Array数组类型原子类AtomicIntegerArray、AtomicLongArray、AtomicReferenceArrayAtomic…...

c语言——数组名该如何理解呢?
一般情况下,数组名表示首元素地址,以下2种除外: ①、sizeof(数组名) 表示整个数组 ※只有数组名的情况 sizeof(数组名i) 就不能表示整个数组 ②、&数组名 表示整个数组,取的是整个数…...

Linux学习笔记13 系统进程管理
前文 Linux学习笔记10 系统启动初始化,服务和进程管理(上)-CSDN博客 Linux学习笔记11 系统启动初始化,服务和进程管理(下)-CSDN博客 Linux学习笔记12 systemd的其他命令-CSDN博客 之前学习了怎么使用sy…...

Spring Boot 项目集成camunda流程引擎
Spring Boot 项目集成camunda流程引擎 camunda地址 camunda中文地址 使用camunda开源工作流引擎有:通过docker运行、使用springboot集成、部署camunda发行包、基于源代码编译运行等多种方式。 文本重点介绍如何在Spring Boot应用程序中如何集成Camunda Platform开…...

2024.12.2工作复盘
1.今天学了什么? 简单的写了一篇博客,是关于参数校验的问题,参数校验,一个是前后端校验到底一不一致,一个是绕过前端校验,看后台的逻辑到底能不能校验住。 2.今天解决了什么问题? 3.今天完成…...

Hot100 - 二叉树的中序遍历
Hot100 - 二叉树的中序遍历 最佳思路: 中序遍历的顺序是:左子树 -> 根节点 -> 右子树。为了实现这个顺序,我们可以利用栈来模拟递归过程,从而避免栈溢出的问题。在遍历过程中,始终向左子树深入,直到…...

docker build ubuntu ssh
dockerfile 构建镜像 为了使用Dockerfile构建Docker镜像,请遵循以下步骤: 创建一个名为Dockerfile的文件,并在其中定义镜像的构建指令。 FROM swr.cn-north-4.myhuaweicloud.com/ddn-k8s/docker.io/ubuntu:24.04# 安装openssh-server和pas…...

三维路径规划|基于黑翅鸢BKA优化算法的三维路径规划Matlab程序
三维路径规划|基于黑翅鸢BKA优化算法的三维路径规划Matlab程序 文章目录 前言三维路径规划|基于黑翅鸢BKA优化算法的三维路径规划Matlab程序基于黑翅鸢BKA优化算法的三维路径规划一、研究基本原理二、黑翅鸢BKA优化算法的基本步骤:三、详细流程四、总结 二、实验结果…...

day01(Linux底层)基础知识
目录 导学 基础知识 1、Bootloader是什么 2、Bootloader的基本作用 3、入式中常见的Bootloader有哪些 4、Linux系统移植为什么要使用bootloader 5、uboot和Bootloader之间的关系 6.Uboot的获取 7、uboot版本命名 8、uboot版本选择 9、uboot的特点 10.Uboot使用 导学…...
—— 重试机制和维表join)
flink学习(13)—— 重试机制和维表join
重试机制 当任务出现异常的时候,会直接停止任务——解决方式,重试机制 1、设置checkpoint后,会给任务一个重启策略——无限重启 2、可以手动设置任务的重启策略 代码设置 //开启checkpoint后,默认是无限重启,可以…...

第三方Cookie的消亡与Google服务器端标记的崛起
随着互联网用户对隐私保护的关注日益增强,各大浏览器正在逐步淘汰第三方Cookie。这一变革深刻影响了广告商和数字营销人员的用户跟踪和数据分析方式。然而,Google推出的服务器端标记技术为这一挑战提供了新的解决方案。 什么是第三方Cookie? …...

微信小程序——文档下载功能分享(含代码)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Burp Suite 全面解析:开启你的 Web 安全测试之旅
声明! 学习视频来自B站up主 **泷羽sec** 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章,笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其他均与本人以及泷羽sec团队无关&a…...
)
Oracle DataGuard 主备正常切换 (Switchover)
前言 众所周知,DataGuard 的切换分为两种情况: 系统正常情况下的切换:这种方式称为 switchover,是无损切换,不会丢失数据。灾难情况下的切换:这种情况下一般主库已经启动不起来了,称为 failov…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...
