【笔记】离散数学 1-3 章
1. 数理逻辑
1.1 命题逻辑的基本概念
1.1.1 命题的概念
命题(Proposition):是一个陈述句,它要么是真的(true),要么是假的(false),但不能同时为真和假。例如,“北京是中国的首都”是一个真命题;“2+2=5”是一个假命题。
注意:感叹句、祈使句、疑问句都不是命题;陈述句中的悖论,判断结果不惟一确定的不是命题。

简单命题与复合命题
- 简单命题(原子命题):一个不能被进一步分解为更简单的命题的陈述句。例如,“北京是中国的首都”就是一个简单命题。
- 复合命题:由两个或多个简单命题通过逻辑联结词组合而成的命题。例如,“北京是中国的首都并且上海是中国最大的城市”就是由两个简单命题通过“并且”这个联结词组合成的复合命题。
1.1.2 否定、析取、合取连结词
联结词
(Connectives):是用来组合一个或多个命题以形成新的命题的逻辑运算符。常见的联结词包括:
- 否定(Negation),通常表示为 ¬ 或 ~
- 合取(Conjunction),通常表示为 ∧ 或 &
- 析取(Disjunction),通常表示为 ∨ 或 |
- 条件(Conditional),通常表示为 → 或 =>
- 双条件(Biconditional),通常表示为 ↔ 或 <=>

例题2:
将下列命题符号化:
(1) 吴颖既用功又聪明. (2) 吴颖不仅用功而且聪明. (3) 吴颖虽然聪明,但不用功. (4) 张辉与王丽都是三好生. (5) 张辉与王丽是同学.
解:
定义基本的原子命题:
- P:吴颖用功。
- Q:吴颖聪明。
- R:张辉是三好生。
- S:王丽是三好生。
- T:张辉与王丽是同学。
每个命题符号化如下:
(1)吴颖既用功又聪明。
符号化:P∧Q
这里使用了合取联结词 ∧(and)来表示“既…又…”。(2)吴颖不仅用功而且聪明。
符号化:P∧Q
尽管表述方式不同,但逻辑上与第(1)题相同,都是表示吴颖同时具有用功和聪明这两个属性。(3)吴颖虽然聪明,但不用功。
符号化:Q∧¬P使用了合取联结词 ∧ 和否定 ¬ 来表示“虽然…但是…”。这里表示吴颖聪明(Q),并且不是用功的(¬P)。(4)张辉与王丽都是三好生。
符号化:R∧S
使用了合取联结词 ∧ 来表示两个人都满足某个条件,即张辉是三好生(R)且王丽也是三好生(S)。(5)张辉与王丽是同学。
符号化:T
这是一个简单的原子命题,直接用 T 表示张辉与王丽是同学这一事实。
例题3:
将下列命题符号化:(1) 2 或 4 是素数.(2) 2 或 3 是素数.(3) 4 或 6 是素数.(4) 小元元只能拿一个苹果或一个梨.(5) 王小红生于 1975 年或 1976 年.
解
(1) 令 p: 2 是素数, q: 4 是素数, p ∨ q
(2) 令 p: 2 是素数, q: 3 是素数, p ∨ q
(3) 令 p: 4 是素数, q: 6 是素数, p ∨ q
(4) 令 p: 小元元拿一个苹果, q: 小元元拿一个梨,
(p ∧ ¬q) ∨ (¬p ∧ q)
(5) p: 王小红生于 1975 年, q: 王小红生于 1976 年,
(p ∧ ¬q) ∨ (¬p ∧ q) 或 p ∨ q
(1) — (3) 为相容或:表示两个条件中至少一个为真,但也可以同时为真。
(4) — (5) 为排斥或:表示两个条件中恰好有一个为真,不能同时为真也不能同时为假。
符号化时 (5) 可有两种形式,而 (4) 则不能
(4) 小元元只能拿一个苹果或一个梨
解释:这是一个典型的排斥或(exclusive or)的情况。小元元要么拿一个苹果,要么拿一个梨,但不能同时拿两者,也不能什么都不拿。(5) 王小红生于 1975 年或 1976 年
解释:这里存在两种可能的解释:
相容或:王小红可能生于 1975 年,或者生于 1976 年,或者两个年份都可以(虽然实际上一个人不可能同时出生于两个年份)。
排斥或:王小红必须且只能生于 1975 年或 1976 年中的一个年份,不能同时出生在两个年份,也不能都不在这两个年份出生。
1.1.3 蕴含联结词
设 p p p 和 q q q 为两个命题,复合命题“如果 p p p,则 $q $”称作 $ $ 与 q q q 的蕴涵式,记作 p → q p\rightarrow q p→q,并称 p p p 是蕴涵式的前件, q q q 为蕴涵式的后件, → \rightarrow → 称作蕴涵联结词。规定: p p p → \rightarrow → q q q 为假当且仅当 p p p 为真而 q q q 为假。

例题4:
只要天冷,小王就穿羽绒服。
◦ 符号化:𝑝→𝑞
◦ 解释:这里的“只要…就…”结构暗示了一个条件语句,即如果前提条件𝑝(天冷)满足,那么结论𝑞(小王穿羽绒服)必然发生。这是标准的蕴含关系,用逻辑符号表示就是𝑝→𝑞。因为天冷,所以小王穿羽绒服。
◦ 符号化:𝑝→𝑞
◦ 解释:“因为…所以…”同样表达了因果关系,即𝑝(天冷)是𝑞(小王穿羽绒服)发生的充分条件。这也是一种蕴含关系,符号化为𝑝→𝑞。若小王不穿羽绒服,则天不冷。
◦ 符号化:¬𝑞→¬𝑝
◦ 解释:这句话的意思是如果观察到𝑞
(小王穿羽绒服)的否定情况,即小王没穿羽绒服,那么可以推断出𝑝(天冷)的否定情况,即天不冷。这是一种反向的蕴含关系,符号化为¬𝑞→¬𝑝。只有天冷,小王才穿羽绒服。
◦ 符号化:𝑞→𝑝
◦ 解释:“只有…才…”强调了必要条件,即要使𝑞(小王穿羽绒服)成为现实,𝑝(天冷)是必不可少的。换句话说,如果没有𝑝,就没有𝑞。这可以通过𝑞→𝑝来表示。除非天冷,小王才穿羽绒服。
◦ 符号化:𝑞→𝑝
◦ 解释:“除非…才…”与“只有…才…”类似,都在说明𝑝(天冷)是𝑞(小王穿羽绒服)的必要条件。因此,符号化仍然是𝑞→𝑝。除非小王穿羽绒服,否则天不冷。
◦ 符号化:¬𝑞→¬𝑝
◦ 解释:这句话的意思是如果小王不穿羽绒服(¬𝑞),那么我们可以得出天不冷(¬𝑝)的结论。这也是一个反向的蕴含关系,符号化为¬𝑞→¬𝑝。如果天不冷,则小王不穿羽绒服。
◦ 符号化:¬𝑝→¬𝑞
◦ 解释:这句话直接给出了一个条件语句,即如果前提条件¬𝑝
(天不冷)满足,那么结论¬𝑞(小王不穿羽绒服)必然发生。这是另一种形式的蕴含关系,符号化为¬𝑝→¬𝑞。小王穿羽绒服仅当天冷的时候。
◦ 符号化:𝑞→𝑝
◦ 解释:“仅当…时候…”再次强调了必要条件,即𝑝(天冷)是𝑞
(小王穿羽绒服)发生的唯一条件。因此,符号化为𝑞→𝑝。
1.1.4 等价联结词
设 p, q 为两个命题,复合命题 “p 当且仅当 q” 称作 p 与 q 的等价式,记作 p↔q,↔ 称作等价联结词。规定 p↔q 为真当且仅当 p 与 q 同时为真或同时为假。
p↔q 的逻辑关系:p 与 q 互为充分必要条件。这意味着如果 p 为真,则 q 也为真;如果 q 为真,则 p 也为真。同样,如果 p 为假,则 q 也为假;如果 q 为假,则 p 也为假。这种关系在逻辑上是对称的,表明两个命题在逻辑上是等价的。
例题:

解:
(1) 2+2=4 当且仅当 3+3=6。
• 𝑝: 2+2=4 是真的。
• 𝑞: 3+3=6 也是真的。
• 因为 𝑝和 𝑞 都是真的,所以 𝑝↔𝑞是真的。(2) 2+2=4当且仅当 3 是偶数。
• 𝑝: 2+2=4 是真的。
• 𝑞: 3 是偶数,这是假的,因为3是奇数。
• 因为 𝑝 为真而 𝑞 为假,所以 𝑝↔𝑞 是假的。
(3) 2+2=4 当且仅当太阳从东方升起。
• 𝑝: 2+2=4 是真的。
• 𝑞: 太阳从东方升起,这是一个自然规律,是真的。
• 因为 𝑝和 𝑞 都是真的,所以 𝑝↔𝑞 是真的。
(4) 2+2=4 当且仅当美国位于非洲。
• 𝑝: 2+2=4 是真的。
• 𝑞: 美国位于非洲,这是假的,因为美国位于北美洲。
• 因为 𝑝 为真而 𝑞 为假,所以 𝑝↔𝑞 是假的。
(5) 函数 𝑓(𝑥) 在 𝑥0 可导的充要条件是它在 𝑥0 连续。
• 这是一个数学定理,如果一个函数在某个点可导,那么它在该点必然连续。但是,一个函数在某个点连续,并不一定意味着它在该点可导。例如,绝对值函数在0点连续但不可导。
• 因此,这个命题是假的,因为可导性是连续性的一个更强的条件,而不是充要条件。
1.2 命题公式及其赋值
1.2.1 合式公式

几点说明:归纳或递归定义, 元语言与对象语言, 外层括号可以省去
1.2.2 合式公式的层次


1.2.3 公式赋值


1.2.4 真值表
将命题公式A在所有赋值下取值的情况列成表, 称作A的真值表.
构造真值表的步骤:
-
找出公式中所含的全部命题变项p1, p2, … , pn(若无下角标 则按字母顺序排列), 列出 2 n 2^n 2n个全部赋值, 从00…0开始, 按二进制加法, 每次加1, 直至11…1为止.
-
按从低到高的顺序写出公式的各个层次.
-
对每个赋值依次计算各层次的真值, 直到最后计算出公式 的真值为止.
例题:




1.2.5 公式的类型
公式的类型:
(1) 若A在它的任何赋值下均为真, 则称A为重言式或永真式;
(2) 若A在它的任何赋值下均为假, 则称A为矛盾式或永假式;
(3) 若A不是矛盾式, 则称A是可满足式.

注意:重言式是可满足式,但反之不真.
真值表的用途:
求出公式的全部成真赋值与成假赋值, 判断公式的类型
1.3 练习题
练习1:
将下列命题符号化
(1) 豆沙包是由面粉和红小豆做成的.
(2) 苹果树和梨树都是落叶乔木.
(3) 王小红或李大明是物理组成员.
(4) 王小红或李大明中的一人是物理组成员.
(5) 由于交通阻塞,他迟到了.
(6) 如果交通不阻塞,他就不会迟到.
(7) 他没迟到,所以交通没阻塞.
(8) 除非交通阻塞,否则他不会迟到.
(9) 他迟到当且仅当交通阻塞.
解:
(1) 是简单命题 (2) 是合取式
(3) 是析取式(相容或)(4) 是析取式(排斥或)
(5)–(9)题的解:

练习2:

习题3:

解:



2. 命题逻辑等值演算
2.1 等值式
2.1.1 等值式概念

例题1:

解:


2.1.2 基本等值式


特别提示:必须牢记这16组等值式,这是继续学习的基础
2.1.3 等值演算与置换规则
-
等值演算——由已知的等值式推演出新的等值式的过程
-
等值演算的基础:
(1) 等值关系的性质:自反性、对称性、传递性
(2) 基本的等值式
(3) 置换规则(见3)
-
置换规则:设Φ(A)是含公式A的命题公式,Φ(B)是用公式B置换,Φ(A)中所有的A后得到的命题公式,若Φ(B) <=>Φ(A),则 Φ(B) <=> Φ(A)

写题的时候可以省去注明中的置换规则
注意:用等值演算不能直接证明两个公式不等值。

2.1.4 等值演算的应用举例



2.2 析取范式与合取范式
2.2.1 概念


2.2.2 范式的性质
定理2.1
(1) 一个简单析取式是重言式当且仅当它同时含有某个命题变项和它的否定式。
- 例子:
- 假设有一个简单析取式 P∨¬P。
- 根据逻辑的定义,无论 P 是真还是假,P∨¬P 总是为真。
- 因此,P∨¬P 是一个重言式。
- 反之,如果一个简单析取式不包含任何命题变项及其否定式,如 P∨Q,则它不是重言式,因为存在 P 和 Q 都为假的情况,使得整个表达式为假。
(2) 一个简单合取式是矛盾式当且仅当它同时含有某个命题变项和它的否定式。
- 例子:
- 假设有一个简单合取式 P∧¬P。
- 根据逻辑的定义,无论 P 是真还是假,P∧¬P 总是为假。
- 因此,P∧¬P 是一个矛盾式。
- 反之,如果一个简单合取式不包含任何命题变项及其否定式,如 P∧Q,则它不是矛盾式,因为存在 P 和 Q 都为真的情况,使得整个表达式为真。
定理2.2
=(1) 一个析取范式是矛盾式当且仅当它每个简单合取式都是矛盾式。
- 例子:
- 假设有一个析取范式 (P∧¬P)∨(Q∧¬Q)。
- 由于 P∧¬P 和 Q∧¬Q 都是矛盾式,因此整个析取范式也是矛盾式。
- 反之,如果析取范式中有一个简单合取式不是矛盾式,如 (P∧Q)∨(R∧S),则整个析取范式不是矛盾式,因为存在 P,Q,R,S 的某些真值组合使得整个表达式为真。
(2) 一个合取范式是重言式当且仅当它的每个简单析取式都是重言式。
- 例子:
- 假设有一个合取范式 (P∨¬P)∧(Q∨¬Q)。
- 由于 P∨¬P 和 Q∨¬Q 都是重言式,因此整个合取范式也是重言式。
- 反之,如果合取范式中有一个简单析取式不是重言式,如 (P∨Q)∧(R∧¬R),则整个合取范式不是重言式,因为存在 P,Q,R 的某些真值组合使得整个表达式为假。
定理2.3(范式存在定理)
任何命题公式都存在与之等值的析取范式与合取范式
小练习:


例题 5:

解:


2.2.3 极小项与极大项
概念:
在含有n个命题变项的简单合取式(简单析取式)中,若每个命题变项均以文字的形式在其中出现且仅出现一次,而且第i个文字出现在左起第i位上(1 ≤ \leq ≤ i ≤ \leq ≤ n),称这样的简单合取式(简单析取式)为极小项(极大项).
几点说明:
- n个命题变项有 2 n 2^n 2n个极小项和 2 n 2^n 2n个极大项
- 2 n 2^n 2n个极小项(极大项)均互不等值
- 用 m i m_{i} mi表示第i个极小项,其中i是该极小项成真赋值的十进制表示. 用 M i M_{i} Mi表示第i个极大项,其中i是该极大项成假赋值的十进制表示. m i m_{i} mi( M i M_{i} Mi)称为极小项(极大项)的名称.
实例:


2.2.4 主析取范式与主合取范式
概念:

主范式的存在唯一定理:
任何命题公式都存在与之等值的主析取范式和主合取范式,并且是唯一的
2.2.5 求公式主范式的步骤


例题:


2.2.6 主范式的应用







2.3 联结词的完备集
暂时没学,期末考试不严格的出这方面的题。
2.4 习题
第一题:
设A与B为含n个命题变项的公式,判断下列命题是否为真?
(1) A<=>B当且仅当A与B有相同的主析取范式
(2) 若A为重言式,则A的主合取范式为0
(3) 若A为矛盾式,则A的主析取范式为1
(4) 任何公式都能等值地化成{∧, ∨}中的公式
(5) 任何公式都能等值地化成{¬, ->, ∧}中的公式
答:(1)真。(2)假。(3)假。(4)假。(5)真。
说明:
(2) 重言式的主合取范式不含任何极大项,为1.
(3) 矛盾式的主合析范式不含任何极小项, 为0.
(4){∧, ∨}不是完备集,如矛盾式不能写成{∧, ∨}中的公式.
(5) {¬, ->, ∧}是完备集.







解此类问题的步骤:
设简单命题并符号化
用复合命题描述各条件
写出由复合命题组成的合取式
将合取式成析取式(最好是主析取范式)
求成真赋值, 并做出解释和结论


第五题的解题步骤:

第六、七题,用消解法:


3.命题逻辑的推理理论
3.1 推理的形式结构
3.1.1 概念



3.1.2 推理定律–重言蕴含式

3.2 自然推理系统P
3.2.1 定义




3.2.2 在自然推理系统P中构造证明


3.2.3 附加前提证明法



3.2.4 归谬法


3.3 习题










相关文章:

【笔记】离散数学 1-3 章
1. 数理逻辑 1.1 命题逻辑的基本概念 1.1.1 命题的概念 命题(Proposition):是一个陈述句,它要么是真的(true),要么是假的(false),但不能同时为真和假。例如…...

AI技术在电商行业中的应用与发展
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

【Linux篇】权限管理 - 用户与组权限详解
一. 什么是权限? 首先权限是限制人的。人 真实的人 身份角色 权限 角色 事物属性 二. 认识人–用户 Linux下的用户分为超级用户和普通用户 root :超级管理员,几乎不受权限的约束普通用户 :受权限的约束超级用户的命令提示符是#,普通用…...

【AI系统】昇腾推理引擎 MindIE
昇腾推理引擎 MindIE 本文将介绍华为昇腾推理引擎 MindIE 的详细内容,包括其基本介绍、关键功能特性以及不同组件的详细描述。 本文内容将深入探讨 MindIE 的三个主要组件:MindIE-Service、MindIE-Torch 和 MindIE-RT,以及它们在服务化部署…...

美畅物联丨智能监控,高效运维:视频汇聚平台在储能领域的实践探索
在当今全球能源格局不断变化的大背景下,对清洁能源的需求正以惊人的速度增长。储能项目作为平衡能源供需、提升能源利用效率的关键环节,其规模和复杂度也在不断攀升。在储能项目的运营管理过程中,安全监控、设备运维以及数据管理等方面面临着…...

[SSL: UNSAFE_LEGACY_RENEGOTIATION_DISABLED]
使用requess库访问https网址时,返回 (Caused by SSLError(SSLError(1, [SSL: UNSAFE_LEGACY_RENEGOTIATION_DISABLED] unsafe legacy renegotiation disabled (_ssl.c:1147)))) 原因可能是服务器的认证方式版本太低然后requests抛弃了这种认证方式 参考ÿ…...

12.2深度学习_视觉处理CNN_池化层、卷积知识
3.池化层 3.1 概述 池化层 (Pooling) 降低维度, 缩减模型大小,提高计算速度. 即: 主要对卷积层学习到的特征图进行下采样(SubSampling)处理。 池化层主要有两种: 最大池化 max pooling 最大池化是从每个局部区域中选择最大值作为池化后的值…...

Kafka 常见面试题深度解析
一、基础概念 1. 请简要介绍 Kafka 的基本架构。 Kafka 主要由生产者(Producer)、消费者(Consumer)、代理(Broker)、主题(Topic)和分区(Partition)等组成。…...

LVS默认的工作模式支持哪些负载均衡算法?
LVS默认的工作模式支持哪些负载均衡算法? LVS(Linux Virtual Server)默认支持多种负载均衡算法,这些算法在不同的场景下具有各自的优势。以下是 LVS 默认支持的负载均衡算法及其特点: 1. 轮询调度(Round Robin Sched…...

洛谷P2670扫雷游戏(Java)
三.P2670 [NOIP2015 普及组] 扫雷游戏 题目背景 NOIP2015 普及组 T2 题目描述 扫雷游戏是一款十分经典的单机小游戏。在 n 行 m列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。玩…...

【算法】【优选算法】位运算(下)
目录 一、:⾯试题 01.01.判定字符是否唯⼀1.1 位图1.2 hash思路1.3 暴力枚举 二、268.丢失的数字2.1 位运算,异或2.2 数学求和 三、371.两整数之和四、137.只出现⼀次的数字 II五、⾯试题 17.19.消失的两个数字 一、:⾯试题 01.01.判定字符是…...

前端性能优化篇:防抖和节流
参考:JS问题:项目中如何区分使用防抖或节流? 面试官:什么是防抖和节流?有什么区别?如何实现? 1 为什么要用到防抖和节流 当函数绑定一些持续触发的事件如:浏览器的resize、scroll…...

同为科技(TOWE)柔性定制化PDU插座
随着科技的进步,越来越多的精密电子设备,成为工作生活密不可分的工具。 电子电气设备的用电环境也变得更为复杂,所以安全稳定的供电是电子电气设备的生命线。 插座插排作为电子电气设备最后十米范围内供配电最终核心部分,便捷、安…...

【云原生系列】云计算中的负载均衡是什么,有什么用
云计算里有一个非常重要的概念叫“负载均衡”,如果你经常听到这个词但还不太明白具体是怎么回事,这篇文章可以给你一些思路。负载均衡简单来说就是“分担压力”,确保访问量被合理地分配到各个服务器上,让系统高效且稳定地运行。 …...

工业—使用Flink处理Kafka中的数据_ChangeRecord2
使用 Flink 消费 Kafka 中 ChangeRecord 主题的数据,每隔 1 分钟输出最近 3 分钟的预警次数最多的 设备,将结果存入Redis 中, key 值为 “warning_last3min_everymin_out” , value 值为 “ 窗口结束时间,设备id” &am…...

【Java-数据结构篇】Java 中栈和队列:构建程序逻辑的关键数据结构基石
我的个人主页 我的专栏:Java-数据结构,希望能帮助到大家!!!点赞❤ 收藏❤ 一、引言 1. 栈与队列在编程中的角色定位 栈和队列作为两种基本的数据结构,在众多编程场景中都有着独特的地位。它们为数据的有序…...

工业—使用Flink处理Kafka中的数据_ProduceRecord1
1 、 使用 Flink 消费 Kafka 中 ProduceRecord 主题的数据,统计在已经检验的产品中,各设备每 5 分钟 生产产品总数,将结果存入Redis 中, key 值为 “totalproduce” , value 值为 “ 设备 id ,最近五分钟生…...

探索CSS版心布局:构建现代网页的黄金比例
探索CSS版心布局:构建现代网页的黄金比例 在网页设计中,版心(或称为内容区域)是页面的核心部分,通常用于放置主要内容。使用CSS3的新特性,可以创建更加灵活和响应式的版心布局。本文将详细介绍如何使用CSS…...

华为NPU服务器昇腾Ascend 910B2部署通义千问Qwen2.5——基于mindie镜像一路试错版(三)
文章目录 前言纯模型推理启动服务后面干什么?这可咋整啊?愁死了!总结前言 这是咱这个系列的第三个文章了。 毕竟,这是我好几天摸索出的经验,能帮助各位在几个小时内领会,我觉得也算是我的功劳一件了。 所以,一是希望大家耐心看下去,耐心操作下去;而是恳请各位多多关…...

详解Java数据库编程之JDBC
目录 首先创建一个Java项目 在Maven中央仓库下载mysql connector的jar包 针对MySQL版本5 针对MySQL版本8 下载之后,在IDEA中创建的项目中建立一个lib目录,然后把刚刚下载好的jar包拷贝进去,然后右键刚刚添加的jar包,点击‘添…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
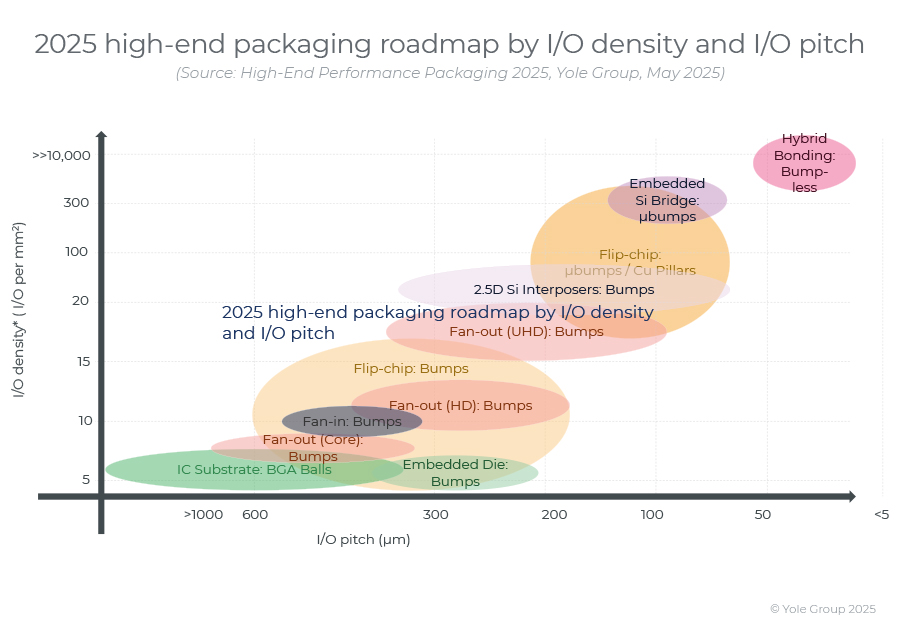
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
