MATLAB 遗传算法

✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。
🍎个人主页:小嗷犬的个人主页
🍊个人网站:小嗷犬的技术小站
🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。
本文目录
- 遗传算法
- MATLAB 实现遗传算法
遗传算法
遗传算法是一种模拟自然界生物进化机制的优化算法,它通过模拟自然选择、交叉和变异等操作来寻找问题的最优解。
遗传算法通常包括以下步骤:
- 定义问题的目标函数和约束条件,以及变量的编码方式。
- 生成初始种群,即一组随机的可行解。
- 计算每个个体的适应度值,即目标函数的值。
- 选择操作,根据适应度值选择一部分个体进入下一代。
- 交叉操作,对选中的个体进行染色体的交换,产生新的个体。
- 变异操作,对某些个体的某些基因进行随机改变,增加种群的多样性。
- 重复3-6步,直到满足终止条件,如达到最大迭代次数或适应度值达到预设阈值。
- 输出最优解或最优解集。
MATLAB 实现遗传算法
MATLAB 中的遗传算法函数为 ga,其基本语法为:
[x,fval] = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon)
其中,fun 为目标函数,nvars 为变量个数,A 为不等式约束系数矩阵,b 为不等式约束右端项,Aeq 为等式约束系数矩阵,beq 为等式约束右端项,lb 为变量下界,ub 为变量上界,nonlcon 为非线性约束函数,intcon 为整数变量的下标。
该函数可以求解线性规划、整数规划、非线性规划、混合整数规划等各种优化问题。
例1
求解以下非线性规划问题:
minf(x)=x12+x22+x32+8\begin{equation} \min \quad f(x)=x_{1}^2+x_{2}^2+x_{3}^2+8 \end{equation} minf(x)=x12+x22+x32+8
s.t. {x12−x2+x32≥0x1+x22+x33≤20−x1−x22+2=0x2+2x32=3x1,x2,x3≥0\begin{equation} \text { s.t. } \left\{ \begin{array}{c} x_{1}^2-x_{2}+x_{3}^2 \geq 0 \\ x_{1}+x_{2}^2+x_{3}^3 \leq 20 \\ -x_{1}-x_{2}^2+2 = 0 \\ x_{2}+2x_{3}^2 = 3 \\ x_{1}, x_{2}, x_{3} \geq 0 \end{array} \right. \end{equation} s.t. ⎩⎨⎧x12−x2+x32≥0x1+x22+x33≤20−x1−x22+2=0x2+2x32=3x1,x2,x3≥0
解
转换为标准形式:
minf(x)=x12+x22+x32+8\begin{equation} \min \quad f(x)=x_{1}^2+x_{2}^2+x_{3}^2+8 \end{equation} minf(x)=x12+x22+x32+8
s.t. {−x12+x2−x32≤0x1+x22+x33−20≤0x1+x22−2=0x2+2x32−3=0x1,x2,x3≥0\begin{equation} \text { s.t. } \left\{ \begin{array}{c} -x_{1}^2+x_{2}-x_{3}^2 \leq 0 \\ x_{1}+x_{2}^2+x_{3}^3-20 \leq 0 \\ x_{1}+x_{2}^2-2 = 0 \\ x_{2}+2x_{3}^2-3 = 0 \\ x_{1}, x_{2}, x_{3} \geq 0 \end{array} \right. \end{equation} s.t. ⎩⎨⎧−x12+x2−x32≤0x1+x22+x33−20≤0x1+x22−2=0x2+2x32−3=0x1,x2,x3≥0
定义目标函数:
function f = objfun(x)f = x(1)^2 + x(2)^2 + x(3)^2 + 8;
end
定义非线性约束函数:
function [c,ceq] = nonlcon(x)c = [-x(1)^2 + x(2) - x(3)^2; x(1) + x(2)^2 + x(3)^3 - 20];ceq = [x(1) + x(2)^2 - 2; x(2) + 2*x(3)^2 - 3];
end
代码求解:
[x,fval] = ga(@objfun,3,[],[],[],[],[0,0,0],[],@nonlcon)
输出结果:
x =0.5516 1.2035 0.9477fval =10.6508
例2
求解以下整数规划问题:
maxZ=4x1+3y1+5y2\begin{equation} \max \quad Z=4x_{1}+3y_{1}+5y_{2} \end{equation} maxZ=4x1+3y1+5y2
s.t. {y1,y2are integers2x1+y1+3y2≤36x1+y1≥8x1+y2≥10x1+y1−y2=4x1,y1,y2≥0\begin{equation} \text { s.t. } \left\{ \begin{array}{c} y_{1},y_{2} \text{ are integers} \\ 2 x_{1}+y_{1}+3y_{2} \leq 36 \\ x_{1}+y_{1} \geq 8 \\ x_{1}+y_{2} \geq 10 \\ x_{1}+y_{1}-y_{2} = 4 \\ x_{1}, y_{1}, y_{2} \geq 0 \end{array} \right. \end{equation} s.t. ⎩⎨⎧y1,y2 are integers2x1+y1+3y2≤36x1+y1≥8x1+y2≥10x1+y1−y2=4x1,y1,y2≥0
解
转换为标准形式:
min−Z=−4x1−3y1−5y2\begin{equation} \min \quad -Z=-4x_{1}-3y_{1}-5y_{2} \end{equation} min−Z=−4x1−3y1−5y2
s.t. {y1,y2are integers2x1+y1+3y2≤36−x1−y1≤−8−x1−y2≤−10x1+y1−y2=4x1,y1,y2≥0\begin{equation} \text { s.t. } \left\{ \begin{array}{c} y_{1},y_{2} \text{ are integers} \\ 2x_{1}+y_{1}+3y_{2} \leq 36 \\ -x_{1}-y_{1} \leq -8 \\ -x_{1}-y_{2} \leq -10 \\ x_{1}+y_{1}-y_{2} = 4 \\ x_{1}, y_{1}, y_{2} \geq 0 \end{array} \right. \end{equation} s.t. ⎩⎨⎧y1,y2 are integers2x1+y1+3y2≤36−x1−y1≤−8−x1−y2≤−10x1+y1−y2=4x1,y1,y2≥0
代码求解:
fun = @(x) -4*x(1) - 3*x(2) - 5*x(3);
A = [2, 1, 3; -1, -1, 0; -1, 0, -1];
b = [36; -8; -10];
Aeq = [1, 1, -1];
beq = 4;
lb = [0, 0, 0];
ub = [];
intcon = [2, 3];
[x,fval] = ga(fun,3,A,b,Aeq,beq,lb,ub,[],intcon);
fval = -fval;
输出结果:
x =4.0000 7.0000 7.0000fval =72.0000
相关文章:

MATLAB 遗传算法
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。 🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心&…...

探讨 Java 中 valueOf 和 parseInt 的区别
前言 在编程中,遇到类型转换,好像会经常用到 parseInt 和 valueOf,当然这里只拿 Integer 类型进行陈述,其他类型也是雷同的; 想必有读者也跟我一样,经常交叉使用这两个方法,但却不知道这两者到…...
JSON学习笔记
♥课程链接:【狂神说Java】一小时掌握JSON_哔哩哔哩_bilibili配套的当然还要学习ajax不管是前端后端,感觉这部分内容是必须的,不然真的做项目的时候云里雾里。总体json的内容不多,具体就:1. 列表、对象等语法格式2. js…...
家政服务小程序实战教程07-轮播图组件
小程序中首页一般显示轮播图的功能,点击轮播图会跳转到具体的一篇文章或者是产品,本篇我们就介绍一下轮播图功能的开发 01 设计数据源 我们轮播图组件需要两个字段,一个是展示的图片,一个是跳转页面传入的参数。打开数据源&…...

MySQL之索引创建、删除、唯一索引、普通索引、及命名规则、注意事项
一、MySQL 索引 定义 索引是一个数据结构,用于加速数据库表中数据的查询。索引存储了一些数据表中的列值,以及这些列值在数据表中的位置,这样就可以通过索引来快速查找到数据表中的某一行数据。 MySQL 支持多种索引类型,包括普通…...

【C++设计模式】学习笔记(3):策略模式 Strategy
目录 简介动机(Motivation)模式定义结构(Structure)要点总结笔记结语简介 Hello! 非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~ ଘ(੭ˊᵕˋ)੭ 昵称:海轰 标签:程序猿|C++选手|学生 简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金…...
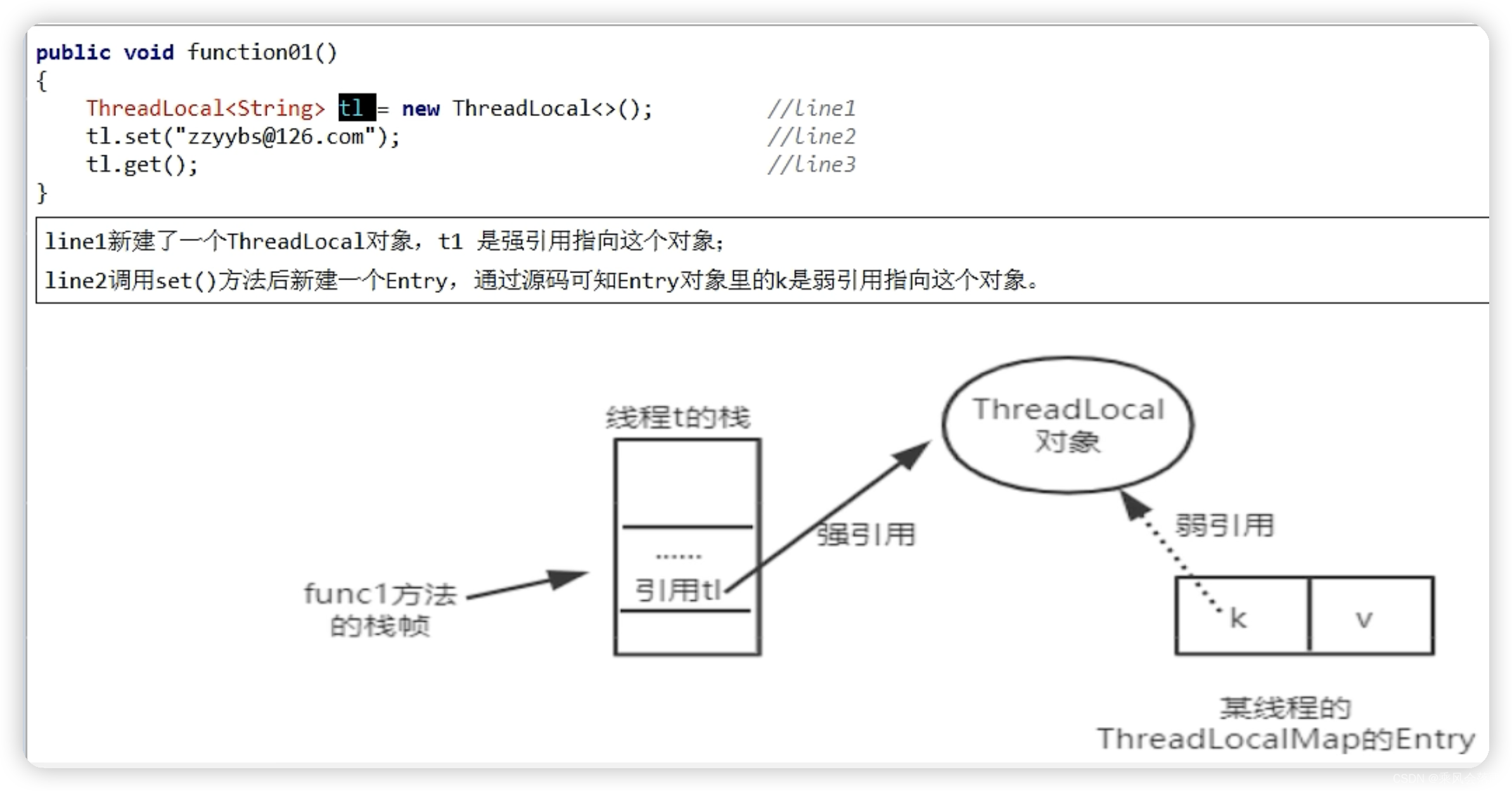
Java——聊聊JUC中的ThreadLocal
文章目录: 1.什么是ThreadLocal? 1.1 api介绍 1.2 最简单的案例认识ThreadLocal 1.3 线程池结合ThreadLocal案例 2.Thread &ThreadLocal & ThreadLocalMap 3.ThreadLocal内存泄漏问题 3.1 四大引用之强引用 3.2 四大引用之软引用 3.3 四…...
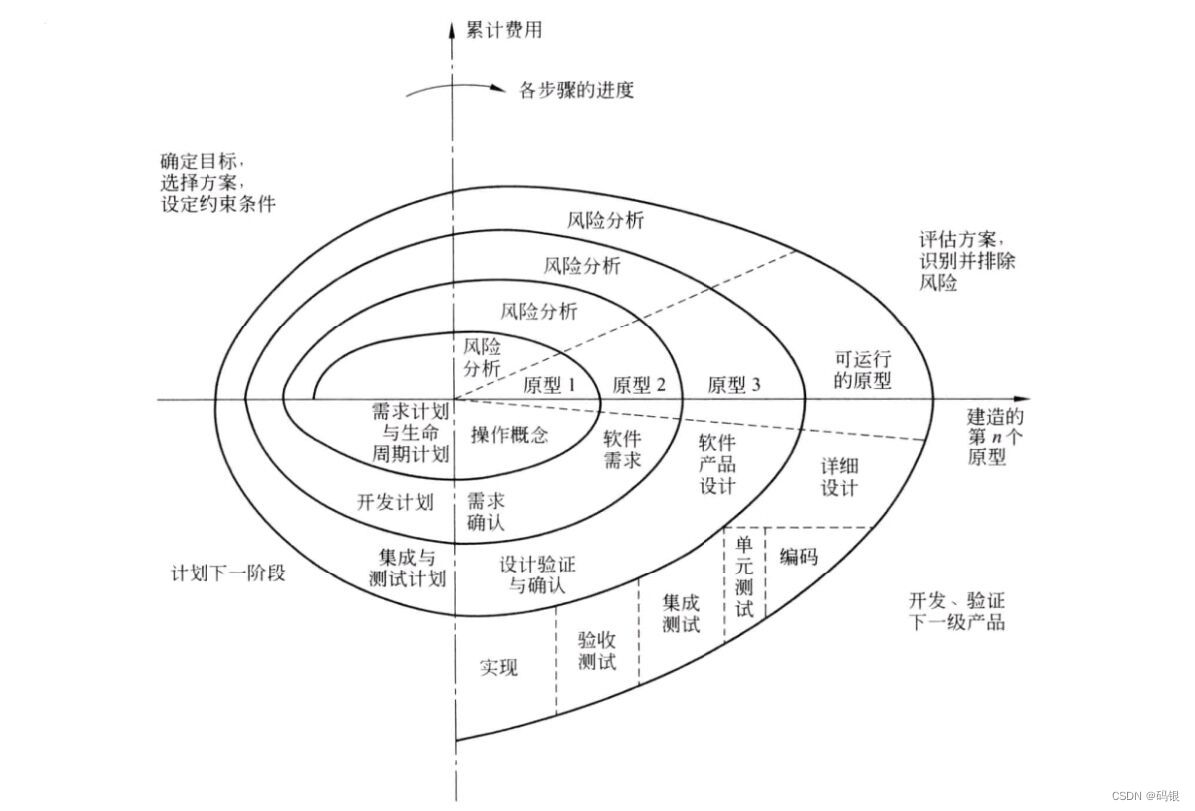
软件工程(4)--螺旋模型
前言 这是基于我所学习的软件工程课程总结的第四篇文章。 在软件开发过程中必须及时识别和分析风险,并且采取适当措施以消除或减少风险的危害。构建原型是一种能使某些类型的风险降至最低的方法。为了降低交付给用户的产品不能满足用户需要的风险,一种行…...

图解LeetCode——剑指 Offer 50. 第一个只出现一次的字符
一、题目 在字符串 s 中找出第一个只出现一次的字符。如果没有,返回一个单空格。 s 只包含小写字母。 二、示例 2.1> 示例 1: 【输入】s "abaccdeff" 【输出】b 2.2> 示例 2: 【输入】s "" 【输出】 限制: 0 < s 的…...

《HTML 5与CSS 3核心技法》读书笔记
目录前言第1章 写在前面第2章 HTML 语法基础第3章 布局类元素 ,房子的楼板、柱子和大梁第4章 功能类元素,房子的门、窗、水管和电气第5章 CSS基础第6章 选择器,确定样式的作用范围选择器类型选择器的组合使用第7章 权重,样式发送冲…...

【沐风老师】3DMAX几何投影插件Geometry Projection使用详解
【几何投影插件】 描述 3DMAX几何投影插件Geometry Projection,将一个或多个对象或它的顶点选择沿全局或局部 x、y 或 z 轴投影到另一个对象上。 适用版本 3dMax2013或更高版本 安装设置 插件的安装非常简单,解压后把插件脚本 “geometry_projectio…...

面试问题整理
20200422面试题 1、有nginx为什么还要用gateway 2、factorybean和beanfactory有什么区别 https://www.cnblogs.com/leeego-123/p/12159574.html 2、aop原理 3、ioc原理 4、注解requestbody和responsebody区别。pathvireable和requestparam注解区别,feign客户端的注解…...

“区块链60人”2022赋能中国区块链创新人物名单公布
2022年11月5日,“2022第五届全国高校人工智能大数据区块链教育教学创新论坛”在京隆重召开。此次论坛公布了“区块链60人”2022赋能中国区块链创新人物评选活动获评名单。 本次评选活动通过媒体报道、第三方推荐、专家评选等环节,坚持“公开、公平、公正…...

day2324 数组
文章目录相关概念codeArrayTest08 数组拷贝相关概念 day23课堂笔记 1、数组 1.1、数组的优点和缺点,并且要理解为什么。 第一:空间存储上,内存地址是连续的。 第二:每个元素占用的空间大小相同。 第三:知道首元素的内…...

【Python实战】神仙运气—快看看你的彩票:2千多万元大奖无人领,马上就过期了,下一期的中奖者会是你吗?(纯技术交流)
前言 越努力越幸运 哈喽~我是栗子同学! 特别注意:不管是沉迷赌球,还是沉迷购彩,都是不可取的。本文纯是一个技术学习内容。 听说关注我的人会暴富哦!、 所有文章完整的素材源码都在👇👇 粉丝…...

2023年上半年软考高项信息系统项目管理师2月25日开班
信息系统项目管理师是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目之一,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资…...
数据库(第一天)
文档信息 文档类别正式文档文档编号数据库基础课 1.2-001版本1.2-001文档名称数据库基础课编写负责人/编写时间梁昭东/2023 年 1 月 30 日审核负责人/审核时间年 月 日批准人/批准时间年 月 日 变更记录 日期版本号变更内容修订者2023.01.30v1.2版根据实际情况增删了部分内容…...

一文了解 ArrayList 的扩容机制
了解 ArrayList 在 Java 中常用集合类之间的关系如下图所示: 从图中可以看出 ArrayList 是实现了 List 接口,并是一个可扩容数组(动态数组),它的内部是基于数组实现的。它的源码定义如下: public class A…...

牛态已成选股源码
{牛态已成} {条件选股} {其他类型} N:7; A1:(REF(H,N) HHV(H,((2 * N) 1))); B1:FILTER(A1,N); C1:BACKSET(B1,(N 1)); D1:FILTER(C1,N); A2:(REF(L,N) LLV(L,((2 * N) 1))); B2:FILTER(A2,N); C2:BACKSET(B2,(N 1)); D2:FILTER(C2,N); E1:((REF(LLV(L,(2 * N)),1) REF(…...

Python基础
Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。Python 的设计具有很强的可读性,相比其他语言经常使用英文关键字,其他语言的一些标点符号,它具有比其他语言更有特色语法结构。小编也整理了一套关于学习Python入门…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...
