LeetCode面试题04 检查平衡性
题目:
实现一个函数,检查二叉树是否平衡。在这个问题中,平衡树的定义如下:任意一个节点,其两棵子树的高度差不超过 1。
一、平衡树定义:
二叉树,一种由节点组成的树形数据结构,每个节点最多有两个子节点,分别称作左子节点和右子节点。而平衡二叉树,可不是普通的二叉树,它有着严苛的要求:对于树中的任意一个节点,其两棵子树(左子树和右子树)的高度差不能超过 1。这个定义看似简单,实则暗藏玄机,它关乎二叉树的查找效率、稳定性等诸多性能指标。想象一下,如果一棵二叉树极度不平衡,就如同瘸腿走路,某些操作的耗时会大幅增加,效率大打折扣。
举个例子,在一棵平衡二叉搜索树里,查找一个元素的时间复杂度接近O()。可要是树失衡了,最坏情况下查找时间复杂度能退化成O(
),这差距可就太悬殊了。
二、解题思路拆解
整体思路概述
拿到这道题,要判断一棵二叉树是否平衡,关键在于检查树中每个节点的左右子树高度差是否都不超过 1。所以整体思路是通过遍历二叉树的每个节点,去获取并比较其左右子树的高度,进而得出整棵树是否平衡的结论,通常会采用递归的方式来实现这个过程。
(一)计算子树高度
咱们得先打造一个 “高度测量仪”,也就是一个专门计算以某个节点为根节点的子树高度的函数。递归在这里大展拳脚,其逻辑简洁而巧妙:当节点为空时,好比遇到了树的 “尽头”,高度自然是 0;要是节点非空,那这棵子树的高度就得看它左右 “臂膀”(左右子树)谁更长了,取两者高度最大值,再给它加上 1(把当前节点这一层算上)。以下是用 C 语言展示的代码片段:
//计算树的高度的辅助函数
int treeHeight(struct TreeNode* node) {if (node == NULL) {return 0;}int leftHeight = treeHeight(node->left);int rightHeight = treeHeight(node->right);return (leftHeight > rightHeight? leftHeight : rightHeight) + 1;
}在这段代码里,先是递归地深挖 node 的左子树高度存进 leftHeight,再探寻右子树高度存入 rightHeight,最后掐指一算,挑出大值加 1 返回,完美算出子树高度。
(二)判断节点平衡性与整树遍历
有了测量子树高度的 “神器”,下一步就是打造主函数来宣判二叉树的 “平衡命运” 了。首先要照顾到特殊情况,要是根节点就是空的,那没得说,这棵树妥妥是平衡的,直接返回 true,皆大欢喜。
碰上根节点非空时,就得严肃起来了。先用刚才的函数量出根节点左右子树各自的高度,要是这俩高度差的绝对值大于 1,那这棵树在根节点这儿就 “崴脚” 了,立马返回 false,宣判它不平衡。
但事情还没完,即便当前根节点这关过了,它的子树里说不定还有 “定时炸弹” (不平衡的节点)呢。所以得接着递归调用主函数,分别去审查左子树和右子树是否平衡,只有左右子树都稳稳当当、符合平衡标准,这整棵树才算得上是平衡的,故而最终返回对左右子树递归判断结果的逻辑与(&&)。用代码说话:
bool isBalanced(struct TreeNode* root) {if (root == NULL) {return true;}int leftHeight = treeHeight(root->left);int rightHeight = treeHeight(root->right);if (abs(leftHeight - rightHeight) > 1) {return false;}return isBalanced(root->left) && isBalanced(root->right);
}三、代码实现
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>//定义树的结构体
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
};// 构建二叉树节点的函数(辅助函数,方便创建测试用的二叉树)
struct TreeNode* createNode(int val) {struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));newNode->val = val;newNode->left = NULL;newNode->right = NULL;return newNode;
}// 计算树的高度的辅助函数
int treeHeight(struct TreeNode* node) {if (node == NULL) {return 0;}// 递归计算左子树高度int leftHeight = treeHeight(node->left);// 递归计算右子树高度int rightHeight = treeHeight(node->right);// 取左右子树中较大的高度加1(根节点算一层)作为当前节点所在子树的高度return (leftHeight > rightHeight? leftHeight : rightHeight) + 1;
}bool isBalanced (struct TreeNode* root)
{if (root==NULL){return true;}// 计算左子树高度int leftHeight = treeHeight(root->left);// 计算右子树高度int rightHeight = treeHeight(root->right);// 判断当前节点的左右子树高度差是否超过1,若超过则不平衡if (abs(leftHeight - rightHeight) > 1) {return false;}// 递归地判断左子树和右子树是否平衡return isBalanced(root->left) && isBalanced(root->right);
};int main(){
//构建一个二叉树struct TreeNode* root = createNode(3);root->left = createNode(9);root->right = createNode(20);root->right->left=createNode(15);root->right->right=createNode(7);bool result = isBalanced(root);if (result) {printf("该二叉树是平衡二叉树\n");} else {printf("该二叉树不是平衡二叉树\n");}return 0;
}四、代码实现细节与优化点
上面给出的代码是基于 C 语言结构体实现二叉树节点的经典范例。代码结构清晰,两个函数各司其职,一个专心算高度,一个全力判断平衡。
不过呢,这代码还有优化空间。现在计算子树高度和判断平衡的过程中存在重复计算,每次判断一个节点的平衡性,都要重新完整计算左右子树高度,当树规模大时,计算量冗余严重。优化思路是把高度计算与平衡判断合二为一,一边计算高度一边检查平衡性,一旦发现不平衡就及时止损,不再做无用功。这种改进能大幅削减不必要的计算,提升算法效率。
五、改进代码实现
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>// 定义二叉树节点结构体
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
};// 构建二叉树节点的函数(辅助函数,方便创建测试用的二叉树)
struct TreeNode* createNode(int val) {struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));newNode->val = val;newNode->left = NULL;newNode->right = NULL;return newNode;
}// 优化后的函数,同时计算高度并判断是否平衡,返回值大于等于0表示当前子树的高度,返回 -1表示子树不平衡
int isBalancedAndHeight(struct TreeNode* node) {if (node == NULL) {return 0;}// 递归计算左子树高度并判断平衡性int leftHeight = isBalancedAndHeight(node->left);if (leftHeight == -1) {return -1;}// 递归计算右子树高度并判断平衡性int rightHeight = isBalancedAndHeight(node->right);if (rightHeight == -1) {return -1;}// 检查当前节点的左右子树高度差是否超过1if (abs(leftHeight - rightHeight) > 1) {return -1;}// 返回当前子树高度(左右子树中较大高度 + 1)return (leftHeight > rightHeight? leftHeight : rightHeight) + 1;
}// 判断二叉树是否平衡的主函数,调用优化后的辅助函数进行判断
bool isBalanced(struct TreeNode* root) {return isBalancedAndHeight(root)!= -1;
}int main() {// 构建一个简单的二叉树示例(这里你可以自行修改节点值和结构来测试不同情况)struct TreeNode* root = createNode(3);root->left = createNode(9);root->right = createNode(20);root->right->left=createNode(15);root->right->right=createNode(7);bool result = isBalanced(root);if (result) {printf("该二叉树是平衡二叉树\n");} else {printf("该二叉树不是平衡二叉树\n");}return 0;
}总结与拓展
判断二叉树是否平衡不仅是一道算法面试高频题,更是深入理解二叉树特性的绝佳契机。通过递归手段巧妙遍历、精准测量、严谨比对,我们能稳稳拿捏二叉树的平衡状况。往后再遇到二叉树相关复杂操作,像是构建平衡二叉搜索树、优化树的存储与查找等,这判断平衡的技巧都能派上大用场。
掌握了二叉树平衡判断,就像是拿到了二叉树世界的一把钥匙,诸多神秘大门将徐徐向你敞开。不管是继续刷题深造,还是实际项目里优化数据结构,都能底气十足、游刃有余。要是你对这篇博客内容有啥疑问、想法,或是独到见解,欢迎随时留言交流,咱们一起在算法海洋破浪前行!
相关文章:
LeetCode面试题04 检查平衡性
题目: 实现一个函数,检查二叉树是否平衡。在这个问题中,平衡树的定义如下:任意一个节点,其两棵子树的高度差不超过 1。 一、平衡树定义: 二叉树,一种由节点组成的树形数据结构,每…...

oracle归档模式下的快速热备方法-适合小库
在我们的一些小型的oracle生产库中,有些时候我们可以在不停库且不使用rman的情况下实现数据库的热备。该热备的原理是通过控制数据文件块头的scn号在备份时候不变化,进而保证备份的数据文件数据一致性。 一、环境 数据库版本: 数据库需要开启…...

【机器学习】【分子属性预测】——python读取.tar.gz文件(以OC22数据集为例)
1 Pre-knowledge .tar.gz 文件是一种常见的压缩文件格式,它实际上是两种压缩格式的组合:.tar 和 .gz。 .tar:这是“tape archive”的缩写,是一种打包(archiving)文件格式,用于将多个文件和目录…...

Qt中禁止或管理任务栏关闭窗口的行为
一、前言 作为一个合格的桌面程序,应该具备良好的资源释放的要求,即避免软件退出时,软件界面虽然消失,却假死在后台,只能通过任务管理器强行杀死。这意味着,程序无法通过正常操作进行退出,变成…...

docker的网络类型和使用方式
docker的网络类型 5种网络类型 bridge 默认类型,桥接到宿主机docker0的网络,有点类似于VM虚拟机的NAT网络模型。 案例: docker run --rm -itd --network bridge --name wzy666wzy-bridge alpine host host类型,共享宿主机的网络空间&#…...

二维立柱图|积水类问题
三类问题 求总的积水量求水坑的个数求水坑最深的深度 基本思路 我们需要从列的角度来看第 i i i 列是不是有积水,但我们该如何确定第 i i i 列是否是有积水? 方法是事先维护一个前后缀的最大值, L [ i ] L[i] L[i] 和 R [ i ] R[i] R[…...

vue前端实现导出页面为word(两种方法)
将vue页面导出为word文档,不用写模板,直接导出即可。 第一种方法(简单版) 第一步:安装所需依赖 npm install html-docx-js -S npm install file-saver -S第二步:创建容器,页面使用方法(简单版࿱…...

22. Three.js案例-创建旋转的圆环面
22. Three.js案例-创建旋转的圆环面 实现效果 知识点 WebGLRenderer (WebGL渲染器) THREE.WebGLRenderer 是Three.js中最常用的渲染器,用于将场景渲染到WebGL画布上。 构造器 new THREE.WebGLRenderer(parameters) 参数类型描述parametersObject可选参数对象&…...

Elasticsearch:使用阿里 infererence API 及 semantic text 进行向量搜索
在之前的文章 “Elasticsearch 开放推理 API 新增阿里云 AI 搜索支持”,它详细描述了如何使用 Elastic inference API 来针对阿里的密集向量模型,稀疏向量模型, 重新排名及 completion 进行展示。在那篇文章里,它使用了很多的英文…...

Linux WEB服务器的部署及优化
1.用户常用关于web的信息 1.1.什么是www www是world wide web的缩写,及万维网,也就是全球信息广播的意思。 通常说的上网就是使用www来查询用户所需要的信息。 www可以结合文字、图形、影像以及声音等多媒体,超链接的方式将信息以Internet…...

人工智能大模型LLM开源资源汇总(持续更新)
说明 目前是大范围整理阶段,所以存在大量机翻说明,后续会逐渐补充和完善资料,减少机翻并增加说明。 Github上的汇总资源(大部分英文) awesome-production-machine-learning 此存储库包含一系列精选的优秀开源库&am…...

目标跟踪算法:SORT、卡尔曼滤波、匈牙利算法
目录 1 目标检测 2 卡尔曼滤波 3《从放弃到精通!卡尔曼滤波从理论到实践》视频简单学习笔记 3.1 入门 3.2 进阶 3.2.1 状态空间表达式 3.2.2 高斯分布 3.3 放弃 3.4 精通 4 匈牙利算法 5 《【运筹学】-指派问题(匈牙利算法)》视…...

Java版-图论-拓扑排序与有向无环图
拓扑排序 拓扑排序说明 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列…...

GTC2024 回顾 | 优阅达携手 HubSpot 亮相上海,赋能企业数字营销与全球业务增长
从初创企业入门到成长型企业拓展,再到 AI 驱动智能化运营,HubSpot 为企业的每步成长提供了全方位支持。 2024 年 11 月下旬,备受瞩目的 GTC2024 全球流量大会(上海)成功举办。本次大会汇聚了全国内多家跨境出海领域企业…...

eclipse启动的时候,之前一切很正常,但突然报Reason: Failed to determine a suitable driver class的解决
1、之前项目都是启动正常的,然后运行以后发现启动不了了,还会报错: 2、这个Reason: Failed to determine a suitable driver class,说是没有合适的驱动class spring:datasource:url: jdbc:sqlserver://192.168.1.101:1433;databa…...

_tkinter.TclError: can‘t find package tkdnd Unable to load tkdnd library.解决办法
Traceback (most recent call last): File “tkinterdnd2\TkinterDnD.py”, line 55, in _require _tkinter.TclError: can’t find package tkdnd During handling of the above exception, another exception occurred: Traceback (most recent call last): File “1.导入总表…...
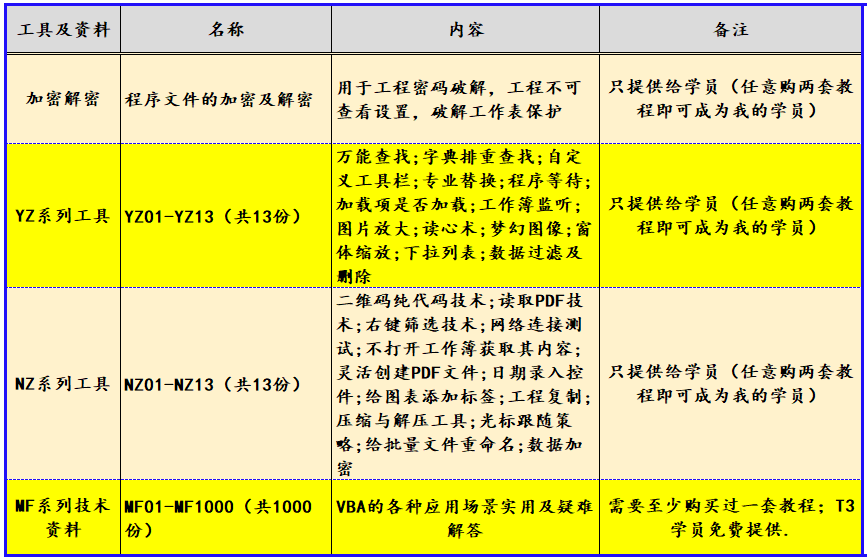
VBA高级应用30例应用在Excel中的ListObject对象:向表中添加注释
《VBA高级应用30例》(版权10178985),是我推出的第十套教程,教程是专门针对高级学员在学习VBA过程中提高路途上的案例展开,这套教程案例与理论结合,紧贴“实战”,并做“战术总结”,以…...

folly库Conv类型转换源码解析
1,普通类型转换 例子1: bool boolV = true;EXPECT_EQ(to<bool>(boolV), true);int intV = 42;EXPECT_EQ(to<int>(intV), 42);float floatV = 4.2f;EXPECT_EQ(to<float>(floatV), 4.2f);double doubleV = 0.42;EXPECT_EQ(to<double>(doubleV), 0.42)…...

UE4 骨骼网格体合并及规范
实现代码 // Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h" #include "SkeletalMeshMerge.h" #include "Kismet/BlueprintFunctionLibrary.h" #include "AceMeshCom…...

Java版企业电子招标采购系统源业码Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看所…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
