最小二乘法拟合出二阶响应面近似模型
背景:根据样本试验数据拟合出二阶响应面近似模型(正交二次型),并使用决定系数R²和调整的决定系数R²_adj来判断二阶响应面模型的拟合精度。
1、样本数据(来源:硕士论文《航空发动机用W形金属密封环密封性能分析与优化》)
编号 x1 x2 x3 x4 y1 y2 y3
1 0.67 0.70 1.78 0.83 804.8 246.7 37.7
2 0.59 0.73 2.09 0.72 686.3 213.5 40.1
3 0.69 0.78 1.81 0.86 703.6 221.0 39.3
4 0.57 0.70 1.84 0.73 822.3 253.6 37.1
5 0.58 0.80 2.07 0.74 632.4 201.6 40.9
6 0.66 0.77 1.95 0.71 716.9 224.7 39.7
7 0.61 0.69 2.04 0.75 730.1 223.3 39.4
8 0.66 0.83 1.88 0.76 676.6 215.8 40.0
9 0.71 0.66 1.85 0.77 845.0 254.6 37.8
10 0.64 0.72 1.73 0.82 813.2 251.8 37.2
11 0.71 0.71 1.99 0.81 709.0 217.4 40.1
12 0.60 0.77 1.91 0.79 698.2 219.5 39.2
13 0.70 0.65 1.94 0.80 794.9 237.9 38.7
14 0.74 0.74 1.96 0.89 663.2 205.7 40.8
15 0.74 0.67 1.74 0.87 839.3 253.8 37.5
16 0.56 0.68 1.87 0.84 773.6 221.6 37.7
17 0.62 0.84 2.06 0.77 598.0 193.0 41.8
18 0.64 0.72 2.01 0.78 703.4 217.3 39.8
19 0.68 0.79 1.79 0.70 777.5 245.8 38.4
20 0.65 0.84 1.81 0.90 640.6 205.3 40.1
21 0.73 0.75 1.76 0.88 743.3 230.9 38.8
22 0.63 0.82 1.70 0.84 726.0 231.4 38.3
23 0.60 0.83 1.90 0.81 648.0 207.5 40.1
24 0.56 0.76 1.97 0.76 693.6 217.9 39.3
25 0.72 0.81 2.03 0.85 600.7 191.7 42.2
2、将上述数据存放在sample_data.xlsx表格中,再编写matlab代码
% % 读取数据(假设数据已经保存在一个名为'data.txt'的文件中,使用空格或制表符分隔)
%% 近似模型:y = a0+a1*x1+a2*x2+a3*x3+a4*x4+a5*x1*x2+a6*x1*x3+a7*x1*x4+a8*x2*x3+a9*x2*x4+a10*x3*x4+a11*x1^2+a12*x2^2+a13*x3^2+a14*x4^2;
clc;clear;
filename = 'sample_data.xlsx';
data = xlsread(filename);% 提取自变量和因变量
X = data(:, 2:5); % x1, x2, x3, x4
y = data(:, 6:8); % y1, y2, y3% 构建扩展自变量矩阵(包括线性项、交互项和平方项)
[n, m] = size(X);
X_extended = ones(n, 1); % 初始化扩展矩阵,第一列为截距项% 添加线性项
X_extended = [X_extended, X];% 添加交互项
X_extended = [X_extended, X(:,1).*X(:,2), X(:,1).*X(:,3), X(:,1).*X(:,4), ...X(:,2).*X(:,3), X(:,2).*X(:,4), X(:,3).*X(:,4)];% 添加平方项
X_extended = [X_extended, X(:,1).^2, X(:,2).^2, X(:,3).^2, X(:,4).^2];% 使用最小二乘法求解回归系数(对每个因变量分别进行)
beta_values = zeros(15, 3); % 15个系数(包括截距项),3个因变量
R2_values = zeros(1, 3);
adjusted_R2_values = zeros(1, 3);for i = 1:3% 拟合模型beta = (X_extended' * X_extended) \ (X_extended' * y(:, i));beta_values(:, i) = beta;% 预测值y_pred = X_extended * beta;% 计算SST, SSE, SSRSST = sum((y(:, i) - mean(y(:, i))).^2);SSE = sum((y(:, i) - y_pred).^2);SSR = SST - SSE;% 计算R^2R2_values(i) = SSR / SST;% 计算调整后的R^2p = size(X_extended, 2); % 自变量数量(包括截距项)adjusted_R2_values(i) = 1 - (1 - R2_values(i)) * ((n - 1) / (n - p));
end% 显示结果
disp('回归系数(包括截距项):');
disp(beta_values);
disp('决定系数 R^2:');
disp(R2_values);
disp('调整的决定系数 Adjusted R^2:');
disp(adjusted_R2_values);3、运行结果

4、如上,决定系数和调整的决定系数均大于0.95,可见,近似模型满足精度要求。
相关文章:

最小二乘法拟合出二阶响应面近似模型
背景:根据样本试验数据拟合出二阶响应面近似模型(正交二次型),并使用决定系数R和调整的决定系数R_adj来判断二阶响应面模型的拟合精度。 1、样本数据(来源:硕士论文《航空发动机用W形金属密封环密封性能分析…...

【汽车】-- 常见的汽车悬挂系统
汽车悬挂系统是车辆的重要组成部分,其主要功能是连接车轮和车身,减缓路面颠簸对车身的影响,提高行驶的平顺性、舒适性和操控性。以下是常见的汽车悬挂系统类型及其特点: 1. 独立悬挂系统 每个车轮可以独立上下运动,不…...

VMware Workstation Pro 17 下载 以及 安装 Ubuntu 20.04.6 Ubuntu 启用 root 登录
1、个人免费版本 VMware Workstation Pro 17 下载链接怎么找?直接咕咕 VMware 找到如下链接。链接如下:Workstation 和 Fusion 对个人使用完全免费,企业许可转向订阅 - VMware 中文博客 点进去链接之后你会看到如下,注意安装之后仍…...

记录ubuntu22.04重启以后无法获取IP地址的问题处理方案
现象描述:我的虚拟机网络设置为桥接模式,输入ifconfig只显示127.0.0.1,不能连上外网。,且无法上网,用ifconfig只有如下显示: 1、sudo -i切换为root用户 2、输入dhclient -v 再输入ifconfig就可以看到多了…...

linux 删除系统特殊的的用户帐号
禁止所有默认的被操作系统本身启动的且不需要的帐号,当你第一次装上系统时就应该做此检查,Linux提供了各种帐号,你可能不需要,如果你不需要这个帐号,就移走它,你有的帐号越多,就越容易受到攻击。 1.为删除你系统上的用户,用下面的…...

core Webapi jwt 认证
core cookie 验证 Web API Jwt 》》》》用户信息 namespace WebAPI001.Coms {public class Account{public string UserName { get; set; }public string UserPassword { get; set; }public string UserRole { get; set; }} }》》》获取jwt类 using Microsoft.AspNetCore.Mvc…...

【Redis】Redis基础——Redis的安装及启动
一、初识Redis 1. 认识NoSQL 数据结构:对于SQL来说,表是有结构的,如字段约束、字段存储大小等。 关联性:SQL 的关联性体现在两张表之间可以通过外键,将两张表的数据关联查询出完整的数据。 查询方式: 2.…...

Oracle Recovery Tools工具一键解决ORA-00376 ORA-01110故障(文件offline)---惜分飞
客户在win上面迁移数据文件,由于原库非归档,结果导致有两个文件scn不一致,无法打开库,结果他们选择offline文件,然后打开数据库 Wed Dec 04 14:06:04 2024 alter database open Errors in file d:\app\administrator\diag\rdbms\orcl\orcl\trace\orcl_ora_6056.trc: ORA-01113:…...

常用环境部署(二十四)——Docker部署开源物联网平台Thingsboard
1、Docker和Docker-compose安装 参考网址如下: CENTOS8.0安装DOCKER&DOCKER-COMPOSE以及常见报错解决_centos8安装docker-compose-CSDN博客 2、 Thingsboard安装 (1)在/home目录下创建docker-compose.yml文件 vim /home/docker-com…...

SqlServer Doris Flink SQL 类型映射关系
SqlServer 对应 Flink SQL 数据类型映射关系 SQL Server TypeFlink SQL Typechar(n)CHAR(n)varchar(n)VARCHAR(n)nvarchar(n)VARCHAR(n)nchar(n)VARCHAR(n)textSTRINGntextSTRINGxmlSTRINGdecimal(p, s)DECIMAL(p, s)moneyDECIMAL(p, s)smallmoneyDECIMAL(p, s)numericNUMERIC…...

Java 中的方法重写
在 Java 中,方法重写(Method Overriding)是面向对象编程的一个重要概念,它指的是子类中存在一个与父类中相同名称、相同参数列表和相同返回类型的方法。方法重写使得子类可以提供特定的实现,从而覆盖(或改变…...

v-for遍历多个el-popover;el-popover通过visible控制显隐;点击其他隐藏el-popover
场景:el-popover通过visible控制显隐;同时el-popover是遍历生成的多个。 原文档的使用visible后就不能点击其他地方使其隐藏;同时解决实现点击其他区域隐藏 <template><div><template v-for="(item,index) in arr" :key="index"><…...

从 Excel 文件中读取数据生成 SQL 语句[快捷main方法]
从 Excel 文件中读取数据生成 SQL 语句的实现 在日常工作中,我们经常需要从 Excel 文件中提取数据,并将其转换为 SQL 插入语句,以便于将数据导入到数据库中。在这篇文章中,我将展示如何使用 Java 来实现这一需求。 项目需求 我…...

从0到1实现项目Docker编排部署
在深入讨论 Docker 编排之前,首先让我们了解一下 Docker 技术本身。Docker 是一个开源平台,旨在帮助开发者自动化应用程序的部署、扩展和管理。自 2013 年推出以来,Docker 迅速发展成为现代软件开发和运维领域不可或缺的重要工具。 Docker 采…...

Vue框架入门
Author:Dawn_T17?? 目录 什么是框架 一.Vue 的使用方向 二.Vue 框架的使用场景 (TIP)MVVM思想 三.Vue入门案例 TIP:插值表达式 四.Vue-指令? (1)v-bind 和 v-model? ? (2&#x…...

vue入门实战(二)父子组件显示,参数传递
经过上次的写法,我们已经写出每个list项,现在要在每个父组件下面加入自己的子项 一、新建子组件: smallItem.vue: <script> export default{props:[text,id,status] //父组件传来的参数 } </script> <template>…...

【Linux】Ubuntu:安装系统后配置
hostname:更改主机名 打开终端。 使用hostnamectl命令更改主机名。 sudo hostnamectl set-hostname 新的主机名你可以使用hostnamectl 命令来验证更改是否成功: hostnamectlChrome:更换默认浏览器 以下是从 Ubuntu 中移除预装的 Snap 版 Fi…...
springboot-查看版本和版本所需JDK
文章目录 访问spring管网查看springboot 项目查看当前版本查看版本所需JDK 访问spring管网 https://spring.io/ 查看springboot 项目 查看当前版本 点击调整到参考文档中去… 查看版本所需JDK...
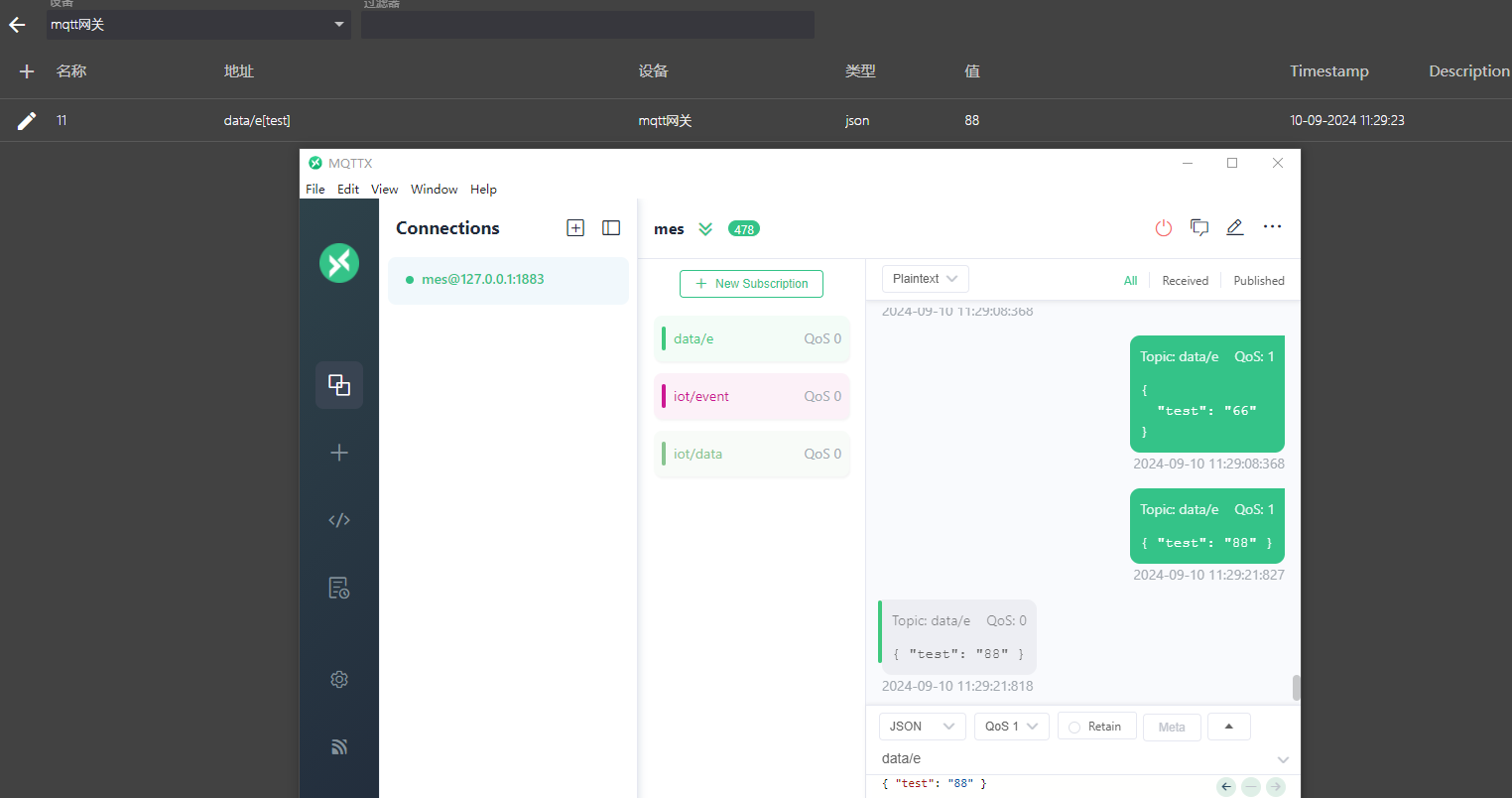
fuxa搭建与使用(web组态)
1. 安装Node.js -> npm安装 参考网址:https://blog.csdn.net/WHF__/article/details/129362462 一、安装运行 C:WINDOWSsystem32>node -v v20.17.0 C:WINDOWSsystem32>npm -v 10.8.2 二、环境配置 在安装路径(D:Program_Files odejs&#x…...
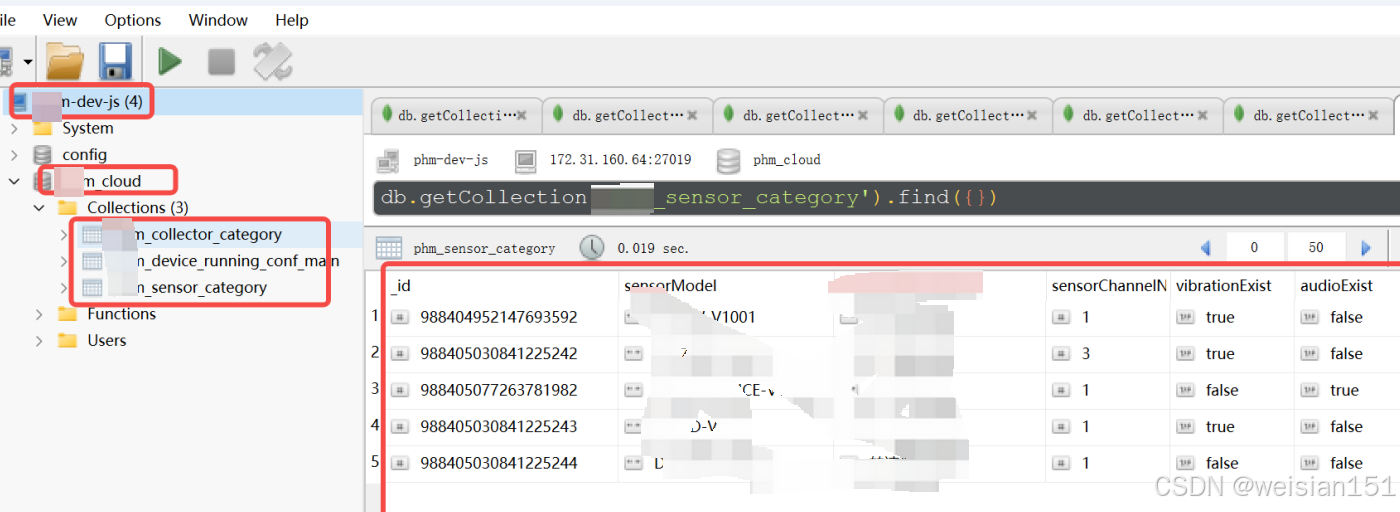
中间件--MongoDB部署及初始化js脚本(docker部署,docker-entrypoint-initdb.d,数据迁移,自动化部署)
一、概述 MongoDB是一种常见的Nosql数据库(非关系型数据库),以文档(Document)的形式存储数据。是非关系型数据库中最像关系型数据库的一种。本篇主要介绍下部署和数据迁移。 在 MongoDB 官方镜像部署介绍中ÿ…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
