主导极点,传递函数零极点与时域模态
运动模态
控制系统的数学建模,可以采用微分方程或传递函数,两者具有相同的特征方程。在数学上,微分方程的解由特解和通解组成,具体求解过程可以参考:微分方程求解的三种解析方法。
如果 n n n阶微分方程,具有 n n n个互不相等的单重特征根 λ 1 , λ 2 , . . . , λ n \lambda_1,\lambda_2,...,\lambda_n λ1,λ2,...,λn,则称 e λ 1 t , e λ 2 t , . . . , e λ n t {e^{{\lambda _1}t}},{e^{{\lambda _2}t}},...,{e^{{\lambda _n}t}} eλ1t,eλ2t,...,eλnt为该系统的模态,也叫振型。每一种模态表示一种类型的运动形态,微分方程的齐次解为它们的线性组合,即
y ( t ) = c 1 e λ 1 t + c 2 e λ 2 t + . . . + c n e λ n t y\left( t \right) = {c_1}{e^{{\lambda _1}t}} + {c_2}{e^{{\lambda _2}t}} + ... + {c_n}{e^{{\lambda _n}t}} y(t)=c1eλ1t+c2eλ2t+...+cneλnt
对于其它类型的特征根类型,所对应的齐次解或模态表达式,如下所示:

极点与模态类型
相同权重下,对比不同模态所对应的冲击响应,结果如下。取传递函数为 1 s + 1 \frac{1}{s+1} s+11、 1 s + 10 \frac{1}{s+10} s+101和 1 s + 100 \frac{1}{s+100} s+1001,对应模态为 e − t e^{-t} e−t、 e − 10 t e^{-10t} e−10t和 e − 100 t e^{-100t} e−100t。所谓权重,指的是模态前的系数(这里均为1)。

clc;clear;close all;sys1 = tf(1, [1 1]); sys2 = tf(1, [1 10]); sys3 = tf(1, [1 100]); t = 0:0.01:10;
[y1, t1] = impulse(sys1, t); [y2, t2] = impulse(sys2, t); [y3, t3] = impulse(sys3, t);figure; hold on;
plot(t1, y1, 'b', 'LineWidth', 1.5); % 蓝色线表示1/(s+1)
plot(t2, y2, 'r', 'LineWidth', 1.5); % 红色线表示1/(s+10)
plot(t3, y3, 'g', 'LineWidth', 1.5); % 绿色线表示1/(s+100)legend('1/(s+1)', '1/(s+10)', '1/(s+100)');
xlabel('Time (s)');ylabel('Impulse Response');grid on;
总结:同等权重情况下,负实部越远离零轴,模态衰减越快;负实部越靠近零轴,模态衰减越慢;
零点与模态权重
将两种模态( e − t e^{-t} e−t和 e − 10 t e^{-10t} e−10t)进行等比例混合,结果如下:
G ( s ) = 0.5 s + 1 + 0.5 s + 10 = s + 5.5 ( s + 1 ) ( s + 10 ) G\left( s \right) = \frac{{0.5}}{{s + 1}} + \frac{{0.5}}{{s + 10}} = \frac{{s + 5.5}}{{\left( {s + 1} \right)\left( {s + 10} \right)}} G(s)=s+10.5+s+100.5=(s+1)(s+10)s+5.5
可以看到,混合的过程产生了一个特定的零点。也就是说,零点不引入新的模态,但却与各模态的相对权重有关。更一般地,假设零点为 − z -z −z,分析权重 α 、 β \alpha、\beta α、β随 z z z的变化规律,如下所示:
G ( s ) = s + z ( s + 1 ) ( s + 10 ) = α s + 1 + β s + 10 = 1 9 z − 1 9 s + 1 + 10 9 − 1 9 z s + 10 {G\left( s \right) = \frac{{s + z}}{{\left( {s + 1} \right)\left( {s + 10} \right)}} = \frac{\alpha }{{s + 1}} + \frac{\beta }{{s + 10}} = \frac{{\frac{1}{9}z - \frac{1}{9}}}{{s + 1}} + \frac{{\frac{{10}}{9} - \frac{1}{9}z}}{{s + 10}}} G(s)=(s+1)(s+10)s+z=s+1α+s+10β=s+191z−91+s+10910−91z

clc;clear;close all;
z = 0:0.5:11; alpha = (1/9) * z - (1/9); beta = (10/9) - (1/9) * z;figure; hold on;
plot(z, alpha, '-', 'LineWidth', 2, 'DisplayName', '\alpha');
plot(z, beta, '-', 'LineWidth', 2, 'DisplayName', '\beta');title('Comparison of \alpha and \beta vs. z'); legend('\alpha', '\beta'); grid on;
xlabel('零点位置'); ylabel('相对权重'); xticks([0,1,5.5,10]); yticks([0,0.5,1]);
总结:零点不引入模态,但却影响模态权重;当极点附近有零点时,对应模态权重明显下降,重叠时甚至会被对消;
输入与最终模态
最终响应模态不仅与系统固有传函有关,还与输入有关。假设系统传递函数为:
G ( s ) = C ( s ) R ( s ) = 6 ( s + 3 ) ( s + 1 ) ( s + 2 ) G\left( s \right) = \frac{{C\left( s \right)}}{{R\left( s \right)}} = \frac{{6\left( {s + 3} \right)}}{{\left( {s + 1} \right)\left( {s + 2} \right)}} G(s)=R(s)C(s)=(s+1)(s+2)6(s+3)
系统包含 e − t e^{-t} e−t、 e − 2 t e^{-2t} e−2t两个运动模态。当输入为 r ( t ) = R 1 + R 2 e − 5 t r\left( t \right) = {R_1} + {R_2}{e^{ - 5t}} r(t)=R1+R2e−5t时,系统最终零状态响应为:
{ c ( t ) = L − 1 [ C ( s ) ] = L − 1 [ 6 ( s + 3 ) ( s + 1 ) ( s + 2 ) ( R 1 s + R 2 s + 5 ) ] = 9 R 1 − R 2 e − 5 t + ( 3 R 2 − 12 R 1 ) e − t + ( 3 R 1 − 2 R 2 ) e − 2 t \left\{ \begin{aligned} c\left( t \right) &= {\mathcal{L}^{ - 1}}\left[ {C\left( s \right)} \right] = {\mathcal{L}^{ - 1}}\left[ {\frac{{6\left( {s + 3} \right)}}{{\left( {s + 1} \right)\left( {s + 2} \right)}}\left( {\frac{{{R_1}}}{s} + \frac{{{R_2}}}{{s + 5}}} \right)} \right] \\ &= 9{R_1} - {R_2}{e^{ - 5t}} + \left( {3{R_2} - 12{R_1}} \right){e^{ - t}} + \left( {3{R_1} - 2{R_2}} \right){e^{ - 2t}} \\ \end{aligned} \right. ⎩ ⎨ ⎧c(t)=L−1[C(s)]=L−1[(s+1)(s+2)6(s+3)(sR1+s+5R2)]=9R1−R2e−5t+(3R2−12R1)e−t+(3R1−2R2)e−2t
其中,前两项具有与输入函数 r ( t ) r(t) r(t)相同的模态;后两项则包含了由系统固有极点形成的模态。
总结
- 同等权重情况下,负实部越远离零轴,模态衰减越快;负实部越靠近零轴,模态衰减越慢;
- 零点不引入模态,但却影响模态权重;当极点附近有零点时,对应模态权重明显下降;
- 最终模态类型与系统极点和输入极点有关;模态权重与系统零点和输入零点有关(严格来说,极点与初始值也会影响权重);
- 当闭环极点同时满足,①靠近零轴,②附近无零点;它将能够在较长时域内决定整体曲线走势,也被称为主导极点;
参考文献
[1] 胡寿松. 自动控制原理 (第六版) [M]. 科学出版社, 2013.
[2] 余成波. 信号与系统 (第二版) [M]. 清华大学出版社, 2007.
[3] CSDN博客:微分方程求解的三种解析方法和Matlab实现:经典时域法(齐次解+特解,零状态+零输入),冲激响应卷积法、传递函数法。
相关文章:

主导极点,传递函数零极点与时域模态
运动模态 控制系统的数学建模,可以采用微分方程或传递函数,两者具有相同的特征方程。在数学上,微分方程的解由特解和通解组成,具体求解过程可以参考:微分方程求解的三种解析方法。 如果 n n n阶微分方程,具…...

永恒之蓝漏洞利用什么端口
永恒之蓝(EternalBlue)是一个著名的漏洞,影响了 Windows 操作系统的 SMBv1 服务。它的漏洞编号是 CVE-2017-0144,该漏洞被用于 WannaCry 等勒索病毒的传播。 永恒之蓝漏洞利用的端口 永恒之蓝漏洞利用的是 SMB(Server…...

网络安全与防范
1.重要性 随着互联网的发达,各种WEB应用也变得越来越复杂,满足了用户的各种需求,但是随之而来的就是各种网络安全的问题。了解常见的前端攻击形式和保护我们的网站不受攻击是我们每个优秀fronter必备的技能。 2.分类 XSS攻击CSRF攻击网络劫…...

Navicat 17 功能简介 | SQL 开发
Navicat 17 功能简介 | SQL 开发 随着 17 版本的发布,Navicat 也带来了众多的新特性,包括兼容更多数据库、全新的模型设计、可视化智能 BI、智能数据分析、可视化查询解释、高质量数据字典、增强用户体验、扩展 MongoDB 功能、轻松固定查询结果、便捷URI…...

嵌入式系统中的并行编程模型:汇总解析与应用
概述:随着嵌入式系统处理能力的不断提升,并行编程在其中的应用愈发广泛。本文深入探讨了多种专门为嵌入式设计的并行编程模型,包括任务队列模型、消息传递模型、数据并行模型、异构多核并行模型、实时任务调度模型以及函数式并行模型。详细阐…...

VulkanSamples编译记录
按照BUILD.md说明,先安装依赖项 sudo apt-get install git build-essential libx11-xcb-dev \libxkbcommon-dev libwayland-dev libxrandr-dev 然后创建一个新文件夹build,在该目录下更新依赖项 cd VulkanSamples mkdir build cd build python ../scr…...
)
使用FabricJS对大图像应用滤镜(巨坑)
背景:我司在canvas的渲染模板的宽高都大于2048px 都几乎接近4000px,就导致使用FabricJS的滤镜功能图片显示异常 新知识:滤镜是对图片纹理的处理 FabricJS所能支持的最大图片纹理是2048的 一但图片超出2048的纹理尺寸 当应用滤镜时,图像会被剪切或者是缩…...

网页502 Bad Gateway nginx1.20.1报错与解决方法
目录 网页报错的原理 查到的502 Bad Gateway报错的原因 出现的问题和尝试解决 问题 解决 网页报错的原理 网页显示502 Bad Gateway 报错原理是用户访问服务器时,nginx代理服务器接收用户信息,但无法反馈给服务器,而出现的报错。 查到…...

Spring基础分析02-BeanFactory与ApplicationContext
大家好,今天和大家一起学习整理一下Spring 的BeanFactory和ApplicationContext内容和区别~ BeanFactory和ApplicationContext是Spring IoC容器的核心组件,负责管理应用程序中的Bean生命周期和配置。我们深入分析一下这两个接口的区别、使用场景及其提供…...

Rerender A Video 技术浅析(五):对象移除与自动配色
Rerender A Video 是一种基于深度学习和计算机视觉技术的视频处理工具,旨在通过智能算法对视频进行重新渲染和优化。 一、对象移除模块 1. 目标检测 1.1 概述 目标检测是对象移除的第一步,旨在识别视频中需要移除的对象并生成相应的掩码(m…...

Java项目实战II基于微信小程序的小区租拼车管理信息系统 (开发文档+数据库+源码)
目录 一、前言 二、技术介绍 三、系统实现 四、核心代码 五、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者,专注于大学生项目实战开发、讲解和毕业答疑辅导。 一、前言 随着城市化进程的加速,小区居民对于出行方…...
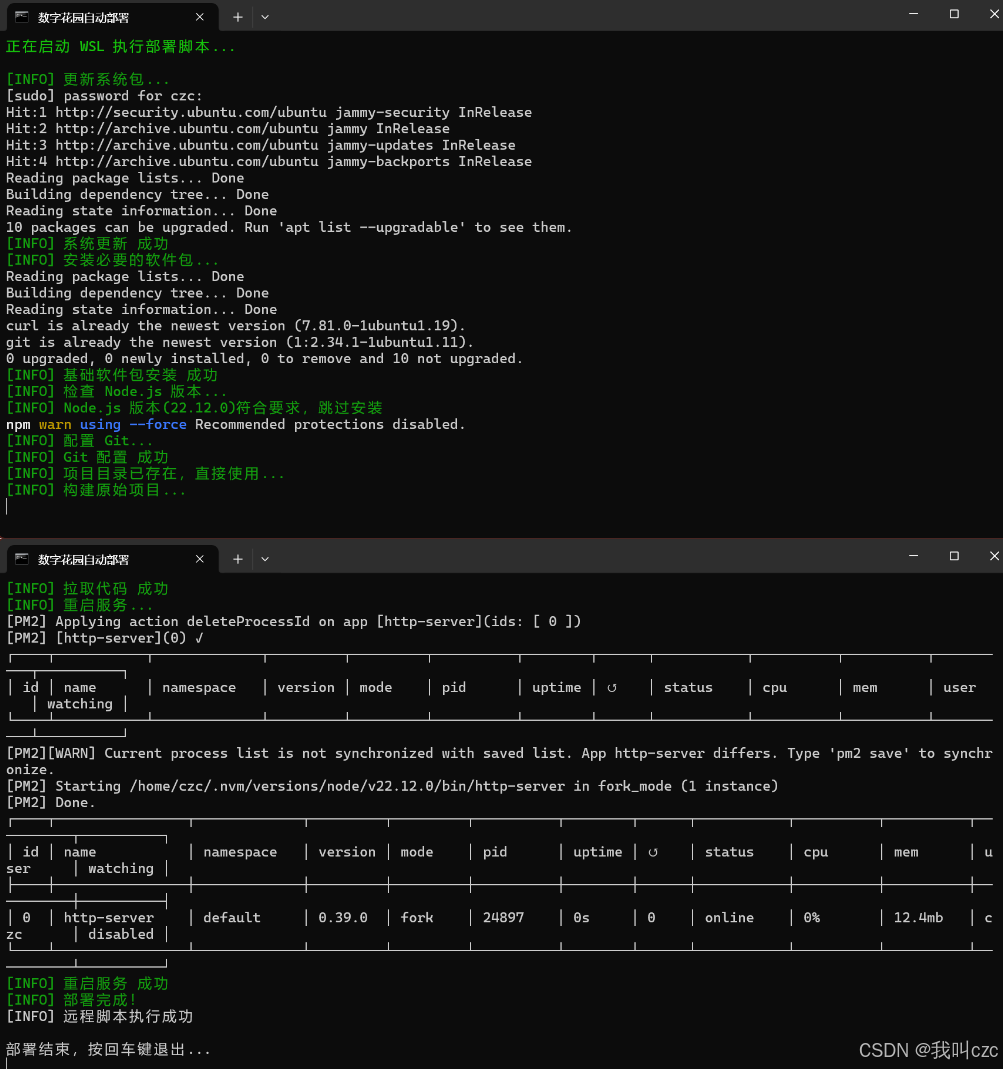
【数字花园】数字花园(个人网站、博客)搭建经历汇总教程
目录 写在最最前面第一章:netlify免费搭建数字花园相关教程使用的平台步骤信息管理 第二章:本地部署数字花园数字花园网站本地手动部署方案1. 获取网站源码2.2 安装 Node.js 3. 项目部署3.1 安装项目依赖3.2 构建项目3.3 启动http服务器 4. 本地预览5. 在…...

WebRTC服务质量(03)- RTCP协议
一、前言: RTCP(RTP Control Protocol)是一种控制协议,与RTP(Real-time Transport Protocol)一起用于实时通信中的控制和反馈。RTCP负责监控和调节实时媒体流。通过不断交换RTCP信息,WebRTC应用…...
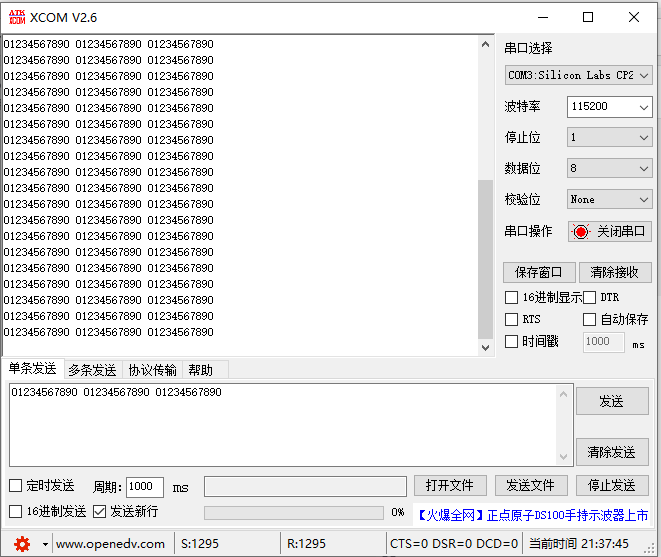
STM32F103单片机HAL库串口通信卡死问题解决方法
在上篇文章 STM32F103单片机使用STM32CubeMX创建IAR串口工程 中分享了使用cubeMX直接生成串口代码的方法,在测试的过程中无意间发现,串口会出现卡死的问题。 当串口一次性发送十几个数据的时候,串口感觉像卡死了一样,不再接收数据…...

Scala正则表达式
一、定义:正则表达式是一种用于匹配、查找和替换文本中特定模式的字符串。 使用方式:①定义一个正则 正则表达式应用场景:查找、验证、替换。 Ⅰ、查找 在目标字符串中,找到符合正则表达式规则要求的 子串。 方括号ÿ…...
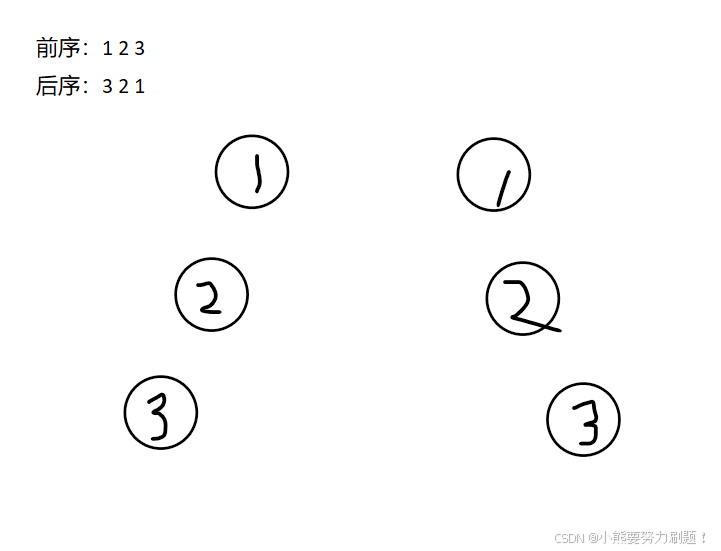
每日一刷——二叉树的构建——12.12
第一题:最大二叉树 题目描述:654. 最大二叉树 - 力扣(LeetCode) 我的想法: 我感觉这个题目最开始大家都能想到的暴力做法就是遍历找到数组中的最大值,然后再遍历一遍,把在它左边的依次找到最大…...
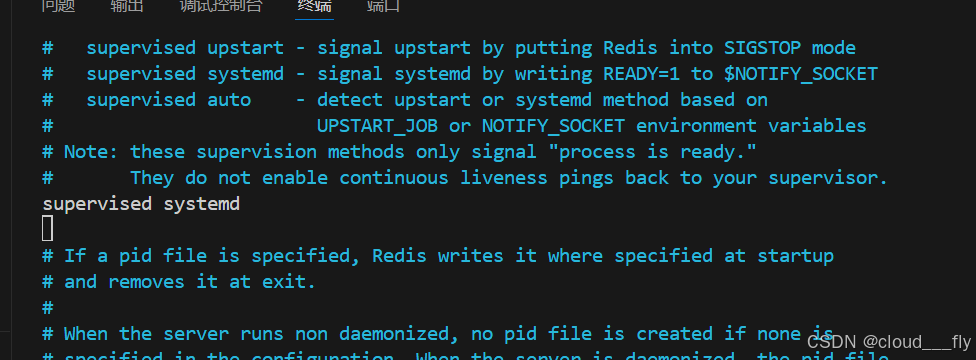
Redis配置文件中 supervised指令
什么是Supervised? supervised模式允许Redis被外部进程管理器监控。通过这个选项,Redis能够在崩溃后自动重启,确保服务的高可用性。常见的进程管理器包括systemd和upstart。 开启方法 vim修改: sudo vi /etc/redis/redis.conf…...
根据基础矩阵(Fundamental Matrix)校正两组匹配点函数correctMatches()的使用)
OpenCV相机标定与3D重建(18)根据基础矩阵(Fundamental Matrix)校正两组匹配点函数correctMatches()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 优化对应点的坐标。 cv::correctMatches 是 OpenCV 库中的一个函数,用于根据基础矩阵(Fundamental Matrix)校…...
python脚本:向kafka数据库中插入测试数据
# coding:utf-8 import datetime import json import random import timefrom kafka import KafkaProducer生产者demo向branch-event主题中循环写入10条json数据注意事项:要写入json数据需加上value_serializer参数,如下代码producer KafkaProducer(val…...
10. 高效利用Excel导入报警信息
高效利用Excel导入报警信息 1.添加报警服务器2.导出报警EXCEL3.报警控件使用1.添加报警服务器 右键项目名称——Add New Sever——Tag Alarm and Event Sever 给报警服务器命名Alarm 给报警服务器分配优先级。如果想要使能历史的话需要和SQL sever配合使用,之前写过。记住这…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
