数值分析——插值法(二)
文章目录
- 前言
- 一、Hermite插值
- 1.两点三次Hermite插值
- 2.两点三次Hermite插值的推广
- 3.非标准型Hermite插值
- 二、三次样条插值
- 1.概念
- 2.三弯矩方程
前言
之前写过Lagrange插值与Newton插值法的内容,这里介绍一些其他的插值方法,顺便复习数值分析.
一、Hermite插值
实际应用中,为了使插值函数更好地切合原函数,不仅要求节点的函数值相等,还要求导数值相同,甚至高阶导数也相等,这类插值问题称为Hermite插值
1.两点三次Hermite插值
给定y=f(x)在节点x0,x1上的函数值和导数值:
y j = f ( x j ) , m j = f ′ ( x j ) , j = 0 , 1. y_j=f(x_j),m_j=f'(x_j),j=0,1. yj=f(xj),mj=f′(xj),j=0,1.
求多项式 H 3 ( x ) H_3(x) H3(x)满足插值条件
H 3 ( x j ) = y j , H 3 ′ ( x j ) = m j , j = 0 , 1. H_3(x_j)=y_j,H'_3(x_j)=m_j,j=0,1. H3(xj)=yj,H3′(xj)=mj,j=0,1.
类似Lagrange插值多项式,我们可以设
H 3 ( x ) = y 0 α 0 ( x ) + y 1 α 1 ( x ) + m 0 β 0 ( x ) + m 1 β 1 ( x ) H_3(x)=y_0\alpha_0(x)+y_1\alpha_1(x)+m_0\beta_0(x)+m_1\beta_1(x) H3(x)=y0α0(x)+y1α1(x)+m0β0(x)+m1β1(x)
为三次Hermite插值多项式,其中 α 0 ( x ) , α 1 ( x ) , β 0 ( x ) , β 1 ( x ) \alpha_0(x),\alpha_1(x),\beta_0(x),\beta_1(x) α0(x),α1(x),β0(x),β1(x)称为Hermite插值基函数.
基函数满足如下条件:
α j ( x j ) = δ j i , α j ′ ( x i ) = 0 , β j ( x i ) = 0 , β j ′ ( x i ) = δ j i , i , j = 0 , 1 \alpha_j(x_j)=\delta_{ji},\alpha'_j(x_i)=0,\\\beta_j(x_i)=0,\beta'_j(x_i)=\delta_{ji},\\ i,j=0,1 αj(xj)=δji,αj′(xi)=0,βj(xi)=0,βj′(xi)=δji,i,j=0,1
其中 δ j i = { 1 j = i 0 j ≠ i \delta_{ji}=\begin{cases}1&j=i\\ 0&j\neq i \end{cases} δji={10j=ij=i
我们可以找到唯一的三次Hermite插值多项式(推导略),即
H 3 ( x ) = y 0 [ 1 + 2 l 1 ( x ) ] l 0 2 ( x ) + y 1 [ 1 + 2 l 0 ( x ) ] l 1 2 ( x ) + m 0 ( x − x 0 ) l 0 2 ( x ) + m 1 ( x − x 1 ) l 1 2 ( x ) H_3(x)=y_0[1+2l_1(x)]l^2_0(x)+y_1[1+2l_0(x)]l^2_1(x)\\+m_0(x-x_0)l^2_0(x)+m_1(x-x_1)l^2_1(x) H3(x)=y0[1+2l1(x)]l02(x)+y1[1+2l0(x)]l12(x)+m0(x−x0)l02(x)+m1(x−x1)l12(x)
这里的 l i l_i li为Lagrange插值基函数, l 0 ( x ) = x − x 1 x 0 − x 1 , l 1 ( x ) = x − x 0 x 1 − x 0 l_0(x)=\frac{x-x_1}{x_0-x_1},l_1(x)=\frac{x-x_0}{x_1-x_0} l0(x)=x0−x1x−x1,l1(x)=x1−x0x−x0
2.两点三次Hermite插值的推广
设 x i ∈ [ a , b ] ( i = 0 , 1 , ⋯ , n ) x_i\in[a,b](i=0,1,\cdots,n) xi∈[a,b](i=0,1,⋯,n)为n+1个互异节点,给定 y = f ( x ) y=f(x) y=f(x)在节点上的函数值和导数值: y j = f ( x j ) , m j = f ′ ( x j ) , j = 0 , ⋯ , n . y_j=f(x_j),m_j=f'(x_j),j=0,\cdots,n. yj=f(xj),mj=f′(xj),j=0,⋯,n.要求插值多项式 H 2 n + 1 ( x ) H_{2n+1}(x) H2n+1(x)满足插值条件
H 2 n + 1 ( x j ) = y j , H 2 n + 1 ′ ( x j ) = m j , j = 0 , ⋯ , n . H_{2n+1}(x_j)=y_j,H'_{2n+1}(x_j)=m_j,j=0,\cdots,n. H2n+1(xj)=yj,H2n+1′(xj)=mj,j=0,⋯,n.有n+1个函数值和n+1个导数值共2n+2个条件,可确定满足插值条件次数不超过2n+1次的多项式 H 2 n + 1 ( x ) H_{2n+1}(x) H2n+1(x).
公式:
H 2 n + 1 = ∑ j = 0 n { f ( x j ) [ 1 − 2 ( x − x j ) l j ′ ( x j ) ] l j 2 ( x ) + f ′ ( x j ) ( x − x j ) l j 2 ( x ) } H_{2n+1}=\sum_{j=0}^n \{f(x_j)[1-2(x-x_j)l'_j(x_j)]l^2_j(x)+f'(x_j)(x-x_j)l^2_j(x)\} H2n+1=j=0∑n{f(xj)[1−2(x−xj)lj′(xj)]lj2(x)+f′(xj)(x−xj)lj2(x)}
其中 l j ( x ) = ( x − x 0 ) ⋯ ( x − x j − 1 ) ( x − x j + 1 ) ⋯ ( x − x n ) ( x j − x 0 ) ⋯ ( x j − x j − 1 ) ( x j − x j + 1 ) ⋯ ( x j − x n ) l_j(x)=\frac{(x-x_0)\cdots(x-x_{j-1})(x-x_{j+1})\cdots(x-x_n)}{(x_j-x_0)\cdots(x_j-x_{j-1})(x_j-x_{j+1})\cdots(x_j-x_n)} lj(x)=(xj−x0)⋯(xj−xj−1)(xj−xj+1)⋯(xj−xn)(x−x0)⋯(x−xj−1)(x−xj+1)⋯(x−xn)
3.非标准型Hermite插值
给出的函数值和导数值不等的情况,例题:

二、三次样条插值
Hermite只保证函数连续或其一阶导数连续,满足不了二阶导数连续的问题. 针对这一问题,产生了样条插值.
1.概念
给定区间[a,b]一个划分:
a = x 0 < x 1 ⋯ < x n − 1 < x n = b a=x_0<x_1\cdots <x_{n-1}<x_n=b a=x0<x1⋯<xn−1<xn=b
若函数S(x)满足
- 在每个小区间 [ x i , x i + 1 ] [x_i,x_{i+1}] [xi,xi+1]是分段三次多项式
- 具有二阶连续导数,即 S ( x ) ∈ C 2 [ a , b ] S(x)\in C^2[a,b] S(x)∈C2[a,b]
- 还满足插值条件: S ( x i ) = f ( x i ) = y i , i = 0 , 1 , 2 , ⋯ , n S(x_i)=f(x_i)=y_i,i=0,1,2,\cdots,n S(xi)=f(xi)=yi,i=0,1,2,⋯,n
则称S(x)为f(x)在[a,b]上的三次样条插值函数,
S ( x ) = { s 0 ( x ) , x ∈ [ x 0 , x 1 ] , s 1 ( x ) , x ∈ [ x 1 , x 2 ] , ⋮ s n − 1 ( x ) , x ∈ [ x n − 1 , x n ] , S(x)=\begin{cases}s_0(x),&x\in [x_0,x_1],\\ s_1(x),&x\in [x_1,x_2],\\ \vdots\\s_{n-1}(x),&x\in [x_{n-1},x_n],\end{cases} S(x)=⎩ ⎨ ⎧s0(x),s1(x),⋮sn−1(x),x∈[x0,x1],x∈[x1,x2],x∈[xn−1,xn],
其中, s i ( x ) s_i(x) si(x)为 [ x i , x i + 1 ] ( i = 0 , 1 , 2 , ⋯ , n − 1 ) [x_i,x_{i+1}](i=0,1,2,\cdots,n-1) [xi,xi+1](i=0,1,2,⋯,n−1)上的三次多项式,设
s i ( x ) = a i x 3 + b i x 2 + c i x + d i ( i = 0 , 1 , ⋯ , n − 1 ) , s_i(x)=a_ix^3+b_ix^2+c_ix+d_i(i=0,1,\cdots,n-1), si(x)=aix3+bix2+cix+di(i=0,1,⋯,n−1),
且满足 s i ( x i ) = y i , s i + 1 ( x i + 1 ) s_i(x_i)=y_i,s_{i+1}(x_{i+1}) si(xi)=yi,si+1(xi+1). 由三次样条函数的定义可知, S ( x ) S(x) S(x)满足下列条件:
{ S ( x i − 0 ) = S ( x i + 0 ) ( i = 1 , 2 , ⋯ , n − 1 ) , S ′ ( x i − 0 ) = S ′ ( x i + 0 ) ( i = 1 , 2 , ⋯ , n − 1 ) , S ′ ′ ( x i − 0 ) = S ′ ′ ( x i + 0 ) ( i = 1 , 2 , ⋯ , n − 1 ) , S ( x i ) = y i ( i = 0 , 1 , 2 , ⋯ , n ) \begin{cases}S(x_i-0)=S(x_i+0)&(i=1,2,\cdots,n-1),\\ S'(x_i-0)=S'(x_i+0)&(i=1,2,\cdots,n-1),\\ S''(x_i-0)=S''(x_i+0)&(i=1,2,\cdots,n-1),\\ S(x_i)=y_i&(i=0,1,2,\cdots,n) \end{cases} ⎩ ⎨ ⎧S(xi−0)=S(xi+0)S′(xi−0)=S′(xi+0)S′′(xi−0)=S′′(xi+0)S(xi)=yi(i=1,2,⋯,n−1),(i=1,2,⋯,n−1),(i=1,2,⋯,n−1),(i=0,1,2,⋯,n)
每个 s i ( x ) s_i(x) si(x)有4个待定系数,所以S(x)共有4n个待定系数,故需4n个方程才能确定. 前面已经得到2n+2(n-1)=4n-2个方程,还缺2个方程. 实际问题通常对样条函数在两个端点处的状态有要求,即所谓的边界条件. 常用的边界条件如下:
第一类边界条件:给定函数在端点处的一阶导数,即
S ′ ( x 0 ) = f 0 ′ , S ′ ( x n ) = f n ′ S'(x_0)=f_0',S'(x_n)=f'_n S′(x0)=f0′,S′(xn)=fn′
第二类边界条件:给定函数在端点处的二阶导数,即
S ′ ′ ( x 0 ) = f 0 ′ ′ , S ′ ′ ( x n ) = f n ′ ′ S''(x_0)=f''_0,S''(x_n)=f_n'' S′′(x0)=f0′′,S′′(xn)=fn′′
第三类边界条件:设 f ( x ) f(x) f(x)是周期函数,并设 x n − x 0 x_n-x_0 xn−x0是一个周期,于是要求 S ( x ) S(x) S(x)满足
S ′ ( x 0 ) = S ′ ( x n ) , S ′ ′ ( x 0 ) = S ′ ′ ( x n ) S'(x_0)=S'(x_n),S''(x_0)=S''(x_n) S′(x0)=S′(xn),S′′(x0)=S′′(xn)
2.三弯矩方程
设 S ′ ′ ( x j ) = M j , j = 0 , 1 , 2 , ⋯ , n S''(x_j)=M_j,j=0,1,2,\cdots,n S′′(xj)=Mj,j=0,1,2,⋯,n,下面计算 S ( x ) S(x) S(x)在 [ x j , x j + 1 ] [x_j,x_{j+1}] [xj,xj+1]的表达式 s j ( x ) s_j(x) sj(x).由于 s j ( x ) s_j(x) sj(x)是三次多项式,故 s j ′ ′ ( x ) s''_j(x) sj′′(x)为线性函数,且 s j ′ ′ ( x j ) = M j , s j ′ ′ ( x j + 1 ) = M j + 1 s_j''(x_j)=M_j,s''_j(x_{j+1})=M_{j+1} sj′′(xj)=Mj,sj′′(xj+1)=Mj+1.由线性插值公式可得
s j ′ ′ ( x ) = x j + 1 − x h j M j + x − x j h j M j + 1 s''_j(x)=\frac{x_{j+1}-x}{h_j}M_j+\frac{x-x_j}{h_j}M_{j+1} sj′′(x)=hjxj+1−xMj+hjx−xjMj+1
其中 h j = x j + 1 − x j h_j=x_{j+1}-x_j hj=xj+1−xj,求积分,可得
s j ( x ) = ( x j + 1 − x ) 3 6 h j M j + ( x − x j ) 3 6 h j M j + 1 + c 1 x + c 2 s_j(x)=\frac{(x_{j+1}-x)^3}{6h_j}M_j+\frac{(x-x_j)^3}{6h_j}M_{j+1}+c_1x+c_2 sj(x)=6hj(xj+1−x)3Mj+6hj(x−xj)3Mj+1+c1x+c2
将插值条件 s j ( x j ) = y j , s j ( x j + 1 ) = y i + 1 s_j(x_j)=y_j,s_j(x_{j+1})=y_{i+1} sj(xj)=yj,sj(xj+1)=yi+1代入,即课确定积分常数 c 1 c_1 c1和 c 2 c_2 c2. 整理后可得 s j ( x ) s_j(x) sj(x)的表达式为 s j ( x ) = ( x j + 1 − x ) 2 6 h j M j + ( x − x j ) 3 6 h j M j + 1 + ( y j − M j h j 2 6 ) x j + 1 − x h j + ( y i + 1 − M j + 1 h j 2 6 ) x − x j h j , j = 0 , 1 , ⋯ , n − 1 s_j(x)=\frac{(x_{j+1}-x)^2}{6h_j}M_j+\frac{(x-x_j)^3}{6h_j}M_{j+1}\\ +\left(y_j-\frac{M_jh_j^2}{6}\right)\frac{x_{j+1}-x}{h_j}+\left(y_{i+1}-\frac{M_{j+1}h_j^2}{6}\right)\frac{x-x_j}{h_j},j=0,1,\cdots,n-1 sj(x)=6hj(xj+1−x)2Mj+6hj(x−xj)3Mj+1+(yj−6Mjhj2)hjxj+1−x+(yi+1−6Mj+1hj2)hjx−xj,j=0,1,⋯,n−1
只需确定 M 0 , M 1 , ⋯ , M n M_0,M_1,\cdots,M_n M0,M1,⋯,Mn的值,即可给出 s j ( x ) s_j(x) sj(x)的表达式,从而可以得到 S ( x ) S(x) S(x)的表达式
s j ′ ( x ) = − ( x j + 1 − x ) 2 2 h j M j + ( x − x j ) 2 2 h j M j + 1 + y j + 1 − y j h j − h j 6 ( M j + 1 − M j ) s'_j(x)=-\frac{(x_{j+1}-x)^2}{2h_j}M_j+\frac{(x-x_j)^2}{2h_j}M_{j+1}+\frac{y_{j+1}-y_j}{h_j}-\frac{h_j}{6}(M_{j+1}-M_j) sj′(x)=−2hj(xj+1−x)2Mj+2hj(x−xj)2Mj+1+hjyj+1−yj−6hj(Mj+1−Mj)
根据条件 s j − 1 ′ ( x j − 0 ) = s j ′ ( x j + 0 ) s_{j-1}'(x_j-0)=s_j'(x_j+0) sj−1′(xj−0)=sj′(xj+0)可知
h j − 1 6 M j − 1 + h j − 1 + h j 3 M j + h j 6 M j + 1 = y j + 1 − y j h j − y j − y j − 1 h j − 1 , h j − 1 h j − 1 + h j M j − 1 + 2 M j + h j h j − 1 + h j M j + 1 = 6 f [ x j , x j + 1 ] − f [ x j − 1 , x j ] h j − 1 + h j , \frac{h_{j-1}}{6}M_{j-1}+\frac{h_{j-1}+h_j}{3}M_j+\frac{h_j}{6}M_{j+1}=\frac{y_{j+1}-y_j}{h_j}-\frac{y_j-y_{j-1}}{h_{j-1}},\\ \frac{h_{j-1}}{h_{j-1}+h_j}M_{j-1}+2M_j+\frac{h_j}{h_{j-1}+h_j}M_{j+1}=6\frac{f[x_j,x_{j+1}]-f[x_{j-1},x_j]}{h_{j-1}+h_j}, 6hj−1Mj−1+3hj−1+hjMj+6hjMj+1=hjyj+1−yj−hj−1yj−yj−1,hj−1+hjhj−1Mj−1+2Mj+hj−1+hjhjMj+1=6hj−1+hjf[xj,xj+1]−f[xj−1,xj],
整理后得到关于 M j − 1 , M j , M j + 1 M_{j-1},M_j,M_{j+1} Mj−1,Mj,Mj+1的方程:
μ j M j − 1 + 2 M j + λ j M j + 1 = d j , \mu_jM_{j-1}+2M_j+\lambda_jM_{j+1}=d_j, μjMj−1+2Mj+λjMj+1=dj,
其中 μ j = h j − 1 h j − 1 + h j , λ j = h j h j − 1 + h j d j = 6 f [ x j − 1 , x j , x j + 1 ] , μ j + λ j = 1 j = 1 , 2 , ⋯ , n − 1 \mu_j=\frac{h_{j-1}}{h_{j-1}+h_j},\lambda_j=\frac{h_j}{h_{j-1}+h_j}\\ d_j=6f[x_{j-1},x_j,x_{j+1}],\mu_j+\lambda_j=1\\ j=1,2,\cdots,n-1 μj=hj−1+hjhj−1,λj=hj−1+hjhjdj=6f[xj−1,xj,xj+1],μj+λj=1j=1,2,⋯,n−1
这里一共有n-1个方程,补充两个方程后可确定 M 0 , M 1 , ⋯ , M n M_0,M_1,\cdots,M_n M0,M1,⋯,Mn共n-1个未知量.
- 第一类边界条件: S ′ ( x 0 ) = f 0 ′ , S ′ ( x n ) = f n ′ S'(x_0)=f'_0,S'(x_n)=f_n' S′(x0)=f0′,S′(xn)=fn′
直接代入 s j ( x ) s_j(x) sj(x)的一阶导数表达式即得
2 M 0 + M 1 = 6 ( ( y 1 − y 0 ) / h 0 − f 0 ′ ) / h 0 ≡ d 0 , M n − 1 + 2 M n = 6 ( f n ′ − ( y n − y n − 1 ) / h n − 1 ) / h n − 1 ≡ d n . 2M_0+M_1=6((y_1-y_0)/h_0-f_0')/h_0\equiv d_0,\\ M_{n-1}+2M_n=6(f'_n-(y_n-y_{n-1})/h_{n-1})/h_{n-1}\equiv d_n. 2M0+M1=6((y1−y0)/h0−f0′)/h0≡d0,Mn−1+2Mn=6(fn′−(yn−yn−1)/hn−1)/hn−1≡dn.
与上面n-1个方程组联立可得n+1阶线性方程组
[ 2 1 μ 1 2 λ 1 μ 2 2 λ 2 ⋱ ⋱ ⋱ μ n − 1 2 λ n − 1 1 2 ] [ M 0 M 1 M 2 ⋮ M n − 1 M n ] = [ d 0 d 1 d 2 ⋮ d n − 1 d n ] \begin{bmatrix}2&1&&&&&\\ \mu_1&2&\lambda_1\\ &\mu_2&2&\lambda_2\\ &&\ddots&\ddots&\ddots\\ &&&\mu_{n-1}&2&\lambda_{n-1}\\ &&&&1&2\end{bmatrix}\begin{bmatrix}M_0\\M_1\\M_2\\ \vdots \\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}d_0\\d_1\\d_2\\ \vdots \\d_{n-1}\\d_n\end{bmatrix} 2μ112μ2λ12⋱λ2⋱μn−1⋱21λn−12 M0M1M2⋮Mn−1Mn = d0d1d2⋮dn−1dn
此方程组的系数矩阵严格对角占优,因此为非奇异矩阵,方程存在唯一解.可用追赶法求出三弯矩方程的解 M j . M_j. Mj. - 第二类边界条件: M 0 = f 0 ′ ′ , M n = f n ′ ′ M_0=f''_0,M_n=f_n'' M0=f0′′,Mn=fn′′
此时只需解n-1阶线性方程组
[ 2 λ 1 μ 2 2 λ 2 ⋱ ⋱ ⋱ μ n − 2 2 λ n − 2 μ n − 1 2 ] [ M 1 M 2 ⋮ M n − 1 M n ] = [ d 1 − μ 1 f 0 ′ ′ d 2 ⋮ d n − 2 d n − 1 − λ n − 1 f n ′ ′ ] \begin{bmatrix}2&\lambda_1&&&\\ \mu_2&2&\lambda_2\\ &\ddots&\ddots&\ddots\\ &&\mu_{n-2}&2&\lambda_{n-2}\\ &&&\mu_{n-1}&2\end{bmatrix}\begin{bmatrix}M_1\\M_2\\ \vdots \\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}d_1-\mu_1f''_0\\d_2\\ \vdots \\d_{n-2}\\d_{n-1}-\lambda_{n-1}f''_n\end{bmatrix} 2μ2λ12⋱λ2⋱μn−2⋱2μn−1λn−22 M1M2⋮Mn−1Mn = d1−μ1f0′′d2⋮dn−2dn−1−λn−1fn′′
此方程严格对角占优,存在唯一解. - 第三类边界条件: S ′ ( x 0 ) = S ′ ( x n ) , S ′ ′ ( x 0 ) = S ′ ′ ( x n ) S'(x_0)=S'(x_n),S''(x_0)=S''(x_n) S′(x0)=S′(xn),S′′(x0)=S′′(xn)
由此边界条件可得 M 0 = M n , λ n M 1 + μ n M n − 1 + 2 M n = d n , M_0=M_n,\\ \lambda_nM_1+\mu_nM_{n-1}+2M_n=d_n, M0=Mn,λnM1+μnMn−1+2Mn=dn,
其中 λ n = h 0 / ( h 0 + h n − 1 ) , μ n = h n − 1 / ( h 0 + h n − 1 ) , d n = 6 [ ( y 1 − y 0 ) / h 0 − ( y n − y n − 1 ) / h n − 1 ] / ( h 0 + h n − 1 ) . \lambda_n=h_0/(h_0+h_{n-1}),\mu_n=h_{n-1}/(h_0+h_{n-1}),\\ d_n=6[(y_1-y_0)/h_0-(y_n-y_{n-1})/h_{n-1}]/(h_0+h_{n-1}). λn=h0/(h0+hn−1),μn=hn−1/(h0+hn−1),dn=6[(y1−y0)/h0−(yn−yn−1)/hn−1]/(h0+hn−1).
与前面n-1个方程联立可得n阶线性方程组:
[ 2 λ 1 μ 2 2 λ 2 ⋱ ⋱ ⋱ μ n − 2 2 λ n − 2 λ n μ 2 2 ] [ M 1 M 2 ⋮ M n − 1 M n ] = [ d 0 d 1 d 2 ⋮ d n − 1 d n ] \begin{bmatrix}2&\lambda_1&&&\\ \mu_2&2&\lambda_2\\ &\ddots&\ddots&\ddots\\ &&\mu_{n-2}&2&\lambda_{n-2}\\ \lambda_n&&&\mu_2&2\end{bmatrix}\begin{bmatrix}M_1\\M_2\\ \vdots \\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}d_0\\d_1\\d_2\\ \vdots \\d_{n-1}\\d_n\end{bmatrix} 2μ2λnλ12⋱λ2⋱μn−2⋱2μ2λn−22 M1M2⋮Mn−1Mn = d0d1d2⋮dn−1dn
此方程组系数矩阵严格对角占优,存在唯一解.
参考书目:《数值分析》张雪莹
相关文章:

数值分析——插值法(二)
文章目录 前言一、Hermite插值1.两点三次Hermite插值2.两点三次Hermite插值的推广3.非标准型Hermite插值 二、三次样条插值1.概念2.三弯矩方程 前言 之前写过Lagrange插值与Newton插值法的内容,这里介绍一些其他的插值方法,顺便复习数值分析. 一、Hermi…...
杨振宁大学物理视频中黄色的字,c#写程序去掉
先看一下效果:(还有改进的余地) 写了个程序消除杨振宁大学物理中黄色的字 我的方法是笨方法,也比较刻板。 1,首先想到,把屏幕打印下来。c#提供了这样一个函数: Bitmap bmp new Bitmap(640, 48…...

uni-app 设置缓存过期时间【跨端开发系列】
🔗 uniapp 跨端开发系列文章:🎀🎀🎀 uni-app 组成和跨端原理 【跨端开发系列】 uni-app 各端差异注意事项 【跨端开发系列】uni-app 离线本地存储方案 【跨端开发系列】uni-app UI库、框架、组件选型指南 【跨端开…...

微信小程序base64图片与临时路径互相转换
1、base64图片转临时路径 /*** 将base64图片转临时路径* param {*} dataurl* param {*} filename* returns*/base64ImgToFile(dataurl, filename "file") {const base64 dataurl; // base64码const time new Date().getTime();const imgPath wx.env.USER_DATA_P…...

蓝桥杯刷题——day2
蓝桥杯刷题——day2 题目一题干题目解析代码 题目二题干解题思路代码 题目一 题干 三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要…...

5.删除链表的倒数第N个节点
19.删除链表的倒数第N个节点 题目: 19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode) 分析: 要删除倒数第几个节点,那么我们需要怎么做呢?我们需要定义两个指针,快指针和慢指针,…...

自己总结:selenium高阶知识
全篇大概10000字(含代码),建议阅读时间30min 一、等待机制 如果有一些内容是通过Ajax加载的内容,那就需要等待内容加载完毕才能进行下一步操作。 为了避免人为操作等待,会遇到的问题, selenium将等待转换…...
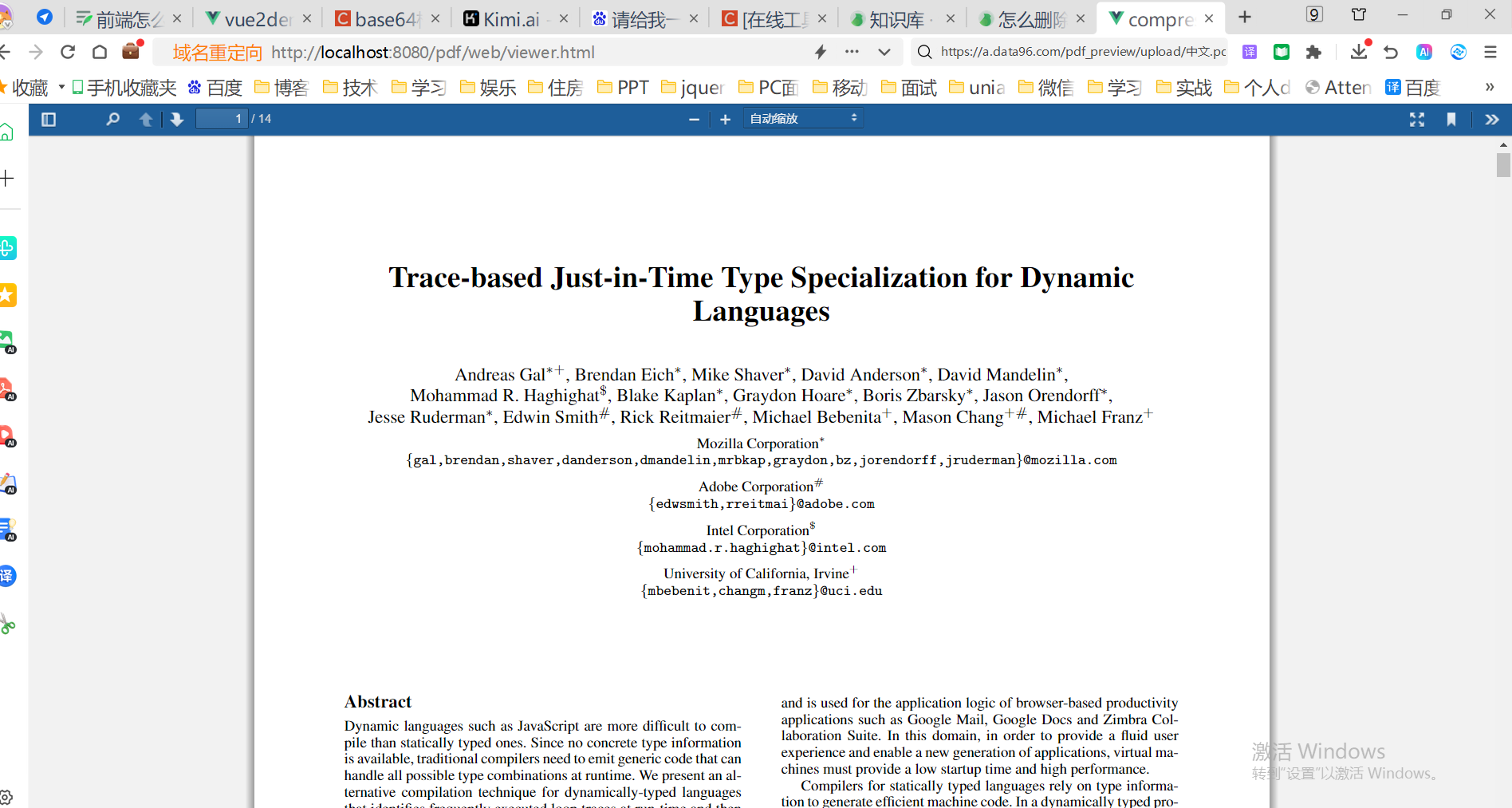
前端怎么预览pdf
1.背景 后台返回了一个在线的pdf地址,需要我这边去做一个pdf的预览(需求1),并且支持配置是否可以下载(需求2),需要在当前页就能预览(需求3)。之前我写过一篇预览pdf的文…...

activemq 的安装部署
下载 https://activemq.apache.org/components/classic/download/# 在/opt目录下载 wget https://dlcdn.apache.org//activemq/5.18.6/apache-activemq-5.18.6-bin.tar.gz解压 tar -zxvf apache-activemq-5.18.6-bin.tar.gz配置java环境 vim /opt/apache-activemq-5.18.6/b…...
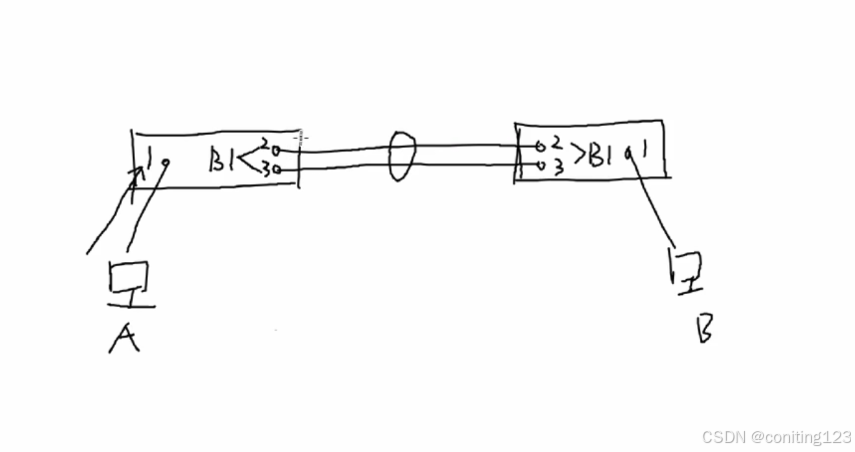
【H3CNE邓方鸣】配置链路聚合+2024.12.11
文章目录 链路聚合作用负载分担分类静态聚合动态聚合 链路聚合作用 定义:把连接到统一交换机上的多个物理端口捆绑为一个逻辑端口 增加链路带宽:聚合组内只要还有物理端口存活,链路就不会中断 提供链路可靠性:避免了STP计算&…...

C语言 学习 日志 递归函数 2024/12/12
C语言 学习 日志 递归函数 介绍: 初始调用:递归函数被首次调用。递归调用:递归函数在其定义中调用自身,创建新的栈帧。基本情况检查:每次递归调用时,检查是否满足基本情况。如果满足,返回结果并开始回溯。…...

【Ubuntu】使用ip link工具创建虚拟局域网并配置?
🦋🦋🦋如何使用ip link工具创建虚拟局域网? sudo ip link add link enx888bd66b7000 name enx.120 type vlan id 120 上述命令使用ip link工具在Linux系统中创建了一个新的虚拟局域网(VLAN)接口,…...
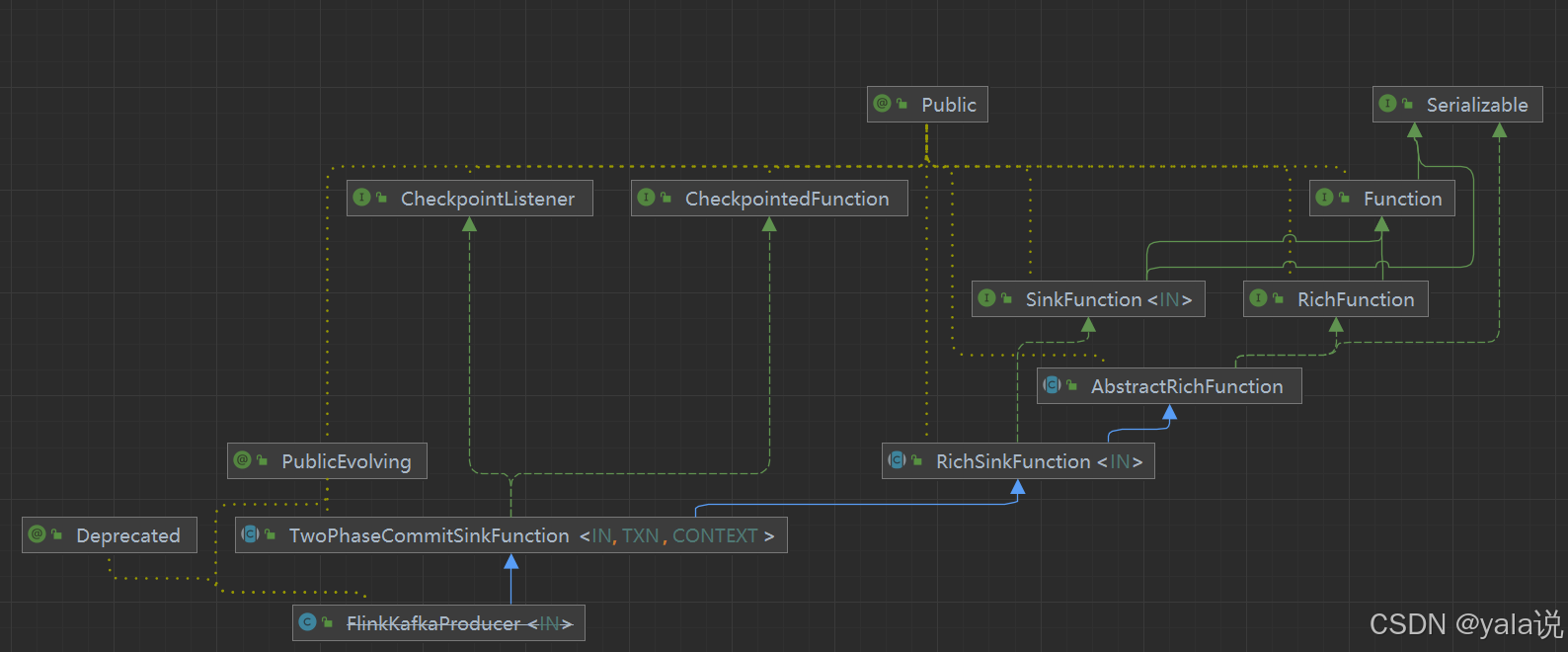
flink sink kafka的事务提交现象猜想
现象 查看flink源码时 sink kafka有事务提交机制,查看源码发现是使用两阶段提交策略,而事务提交是checkpoint完成后才执行,那么如果checkpoint设置间隔时间比较长时,事务未提交之前,后端应该消费不到数据,…...
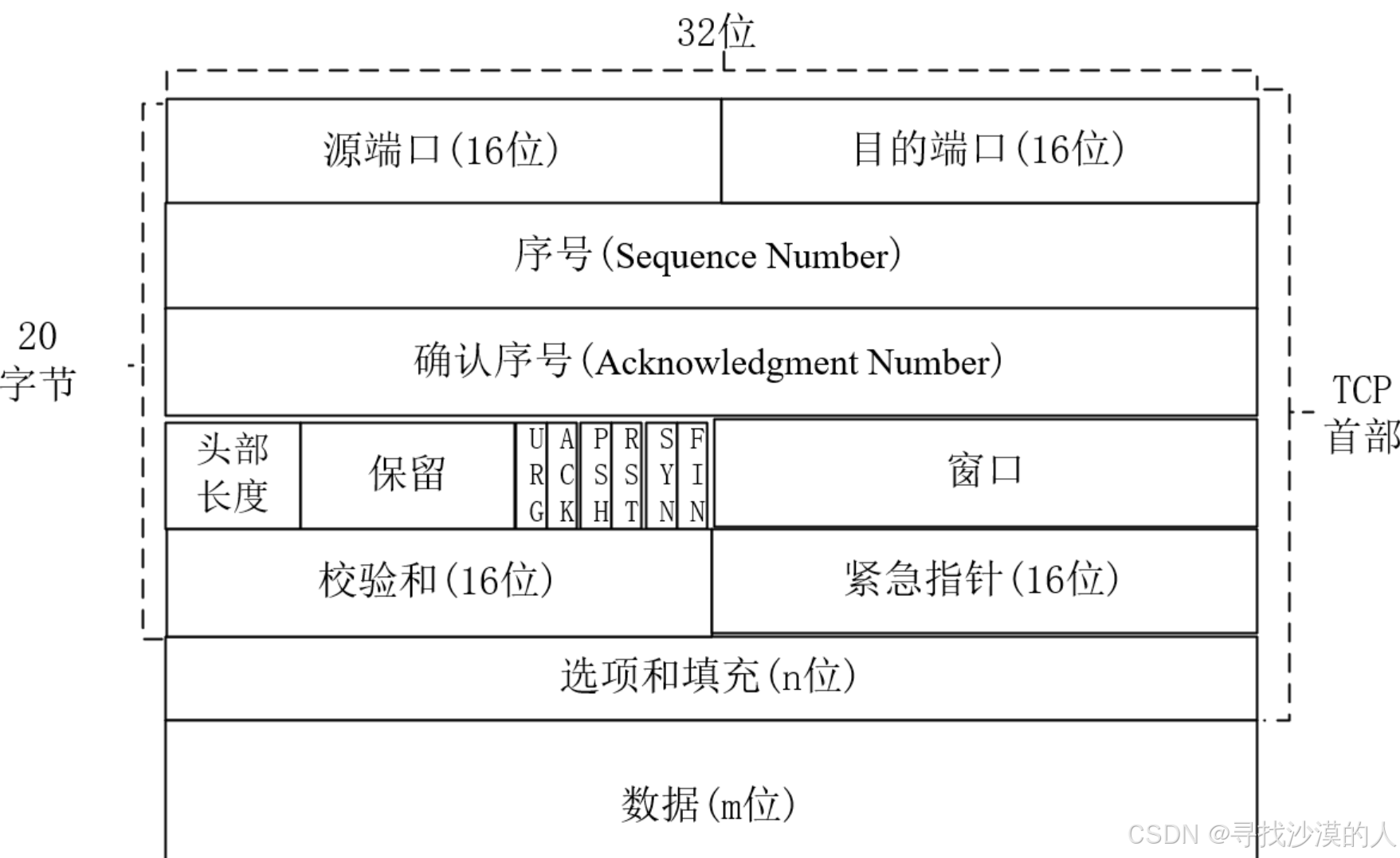
网络原理03
回顾 应用层:应用程序,数据具体如何使用 传输层:关注起点和终点 网络层:关注路径规划 数据链路层:关注相邻节点的转发 物理层:硬件设备 应用层 应用程序 在应用层,很多时候,…...
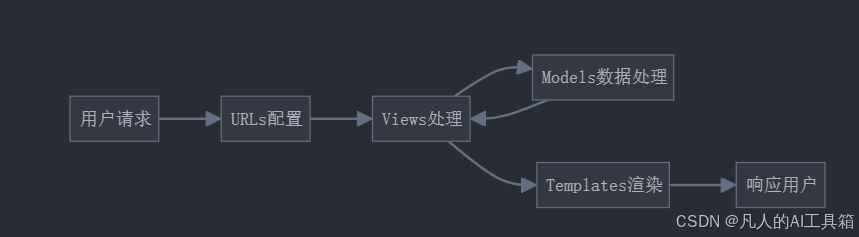
每天40分玩转Django:简介和环境搭建
Django简介和环境搭建 一、课程概述 学习项目具体内容预计用时Django概念Django框架介绍、MVC/MTV模式、Django特点60分钟环境搭建Python安装、pip配置、Django安装、IDE选择45分钟创建项目项目结构、基本配置、运行测试75分钟实战练习创建个人博客项目框架60分钟 二、Djang…...

【蓝桥杯最新板】蓝桥杯嵌入式液晶上实现电子时钟
这几年蓝桥杯比赛比较适合学生技能学习,考虑板子功能,提出完成的任务。 要求在液晶完成如下图效果: 主要是实现液晶显示时钟和数字时钟,具体样式可以依据实际情况微调。 实现过程: 1.需要画圆(外圆、内圆…...
【机器学习】基础知识:拟合度(Goodness of Fit)
拟合度概念及意义 拟合度(Goodness of Fit)是衡量统计模型对数据解释能力的指标,用于评价模型对观测数据的拟合效果。在回归分析、分类模型或其他预测模型中,拟合度是模型性能的重要衡量标准。 1. 拟合度的作用 拟合度的主要作用…...

使用Jackson库在Java应用程序中将Map对象转换为JSON数组字符串,以及反向操作
在现代Java应用程序中,特别是使用RESTful Web服务时,经常需要将Java对象转换为JSON格式,反之亦然。 当表示如用户管理系统中的用户列表这样的数据结构时,将Map转换为JSON数组字符串变得非常有用。在这个指南中,我们将…...
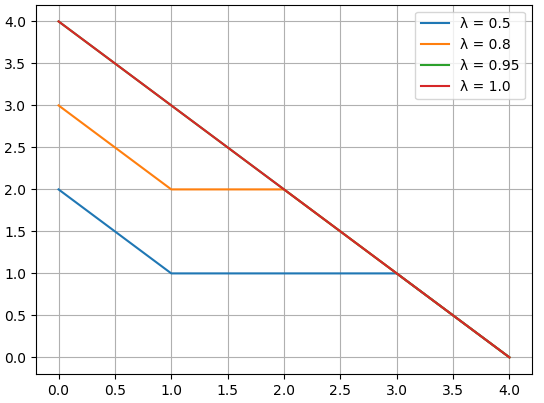
深入解析强化学习中的 Generalized Advantage Estimation (GAE)
中文版 深入解析强化学习中的 Generalized Advantage Estimation (GAE) 1. 什么是 Generalized Advantage Estimation (GAE)? 在强化学习中,计算策略梯度的关键在于 优势函数(Advantage Function) 的设计。优势函数 ( A ( s , a ) A(s, a…...

离开wordpress
wordpress确实挺好用的 插件丰富 主题众多 收费的插件也很多 国内的做主题的也挺好 但是服务器跑起来各种麻烦伤脑筋 需要花在维护的时间太多了 如果你的网站持续盈利 你就会更担心访问质量访问速度 而乱七八糟的爬虫黑客 让你的服务器不堪重负 突然有一天看到了静态站…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
