11- 聚类算法 (KMeans/DBSCAN/agg) (机器学习)
聚类算法
- 聚类算法和降维算法那都属于无监督算法。
- KMeans 是以一个值为中心, 然后所有其他点到该点距离最小值的累积和。
kmeans = KMeans(n_clusters=3) # n_clusters 分类数量
kmeans.fit(data.iloc[:,1:]) # 无监督,只需要给数据X就可以- DBSCAN 算法是以某点为起始点, 如果到该点距离的附近点的数量达到一定数量就可以进入该集合, 类似传销。
dbscan = DBSCAN(eps = 0.2,min_samples=3)
dbscan.fit(X)- agg 算法是先找距离最近的点, 再根据距离的远近进行不断聚合。
agg = AgglomerativeClustering(n_clusters=6,linkage='ward') # 最近的距离,作为标准
agg.fit(X)一 聚类算法介绍
1.1、聚类作用
- 知识发现 发现事物之间的潜在关系
- 异常值检测
- 特征提取 数据压缩的例子

1.2、有监督与无监督学习
- 有监督:
- 给定训练集 X 和 标签Y
- 选择模型
- 学习(目标函数的最优化), 训练fit
- 生成模型(本质上是一组参数、方程)
- 根据生成的一组参数进行预测分类等任务
- 无监督:
- 拿到的数据只有X ,没有标签,只能根据X的相似程度做一些事情。
- Clustering 聚类
- 对于大量未标注的数据集,按照内在相似性来分为多个类别(簇) 目标:类别内相似度大,类别间相似小。
- 也可以用来改变数据的维度,可以将聚类结果作为一个维度添加到训练数据中。
- 降维算法,数据特征变少
1.3、数据间的相似度
- 每一条数据都可以理解为多维空间中的一个点。
- 可以根据点和点之间的距离来评价数据间的相似度
- 近朱者赤近墨者黑!
数据间的距离类型:
- P = 1 曼哈顿距离:
- 在二维空间中可以看出,这种距离是计算两点之间的直角边距离,相当于城市中出租汽车沿城市街道拐直角前进而不能走两点连接间的最短距离。
- P = 2 欧氏距离,就是两点之间的直线距离(以下简称欧氏距离)
- P = 无穷,切比雪夫距离 ,哪个维度差值最大就是哪个差值作为距离。
1.4、余弦距离
将数据看做空间中的点的时候,评价远近可以用欧氏距离或者余弦距离。
计算过程如下:
- 将数据映射为高维空间中的点(向量)
- 计算向量间的余弦值
- 取值范围[-1,+1] 越趋近于1代表越相似,越趋近于-1代表方向相反,0代表正交
- 余弦相似度可以评价文章的相似度,从而实现对文章,进行分类。
二 Kmeans
2.1、聚类原理
- 将N个样本映射到K个簇中
- 每个簇至少有一个样本
基本思路:
- 先给定K个划分,迭代样本与簇的隶属关系,每次都比前一次好一些
- 迭代若干次就能得到比较好的结果
2.2、Kmeans算法原理
算法步骤:
- 选择K个初始的簇中心
- 逐个计算每个样本到簇中心的距离,将样本归属到距离最小的那个簇中心的簇中
- 每个簇内部计算平均值,更新簇中心
- 开始迭代
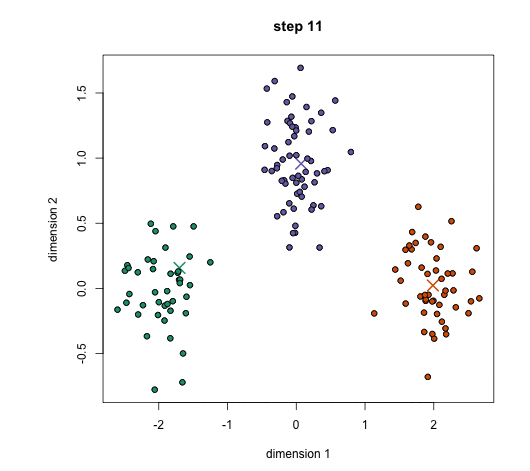
2.3、KMeans优缺点
- 优点:
- 简单,效果不错
- 缺点:
- 对异常值敏感
- 对初始值敏感
- 对某些分布聚类效果不好
2.4、Kmeans损失函数
-
- 其中 μ 是簇的均值向量,或者说是质心。
- 其中
代表每个样本点到均值点的距离(其实也是范数)。
2.5、Kmeans初步使用
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd# 需要将亚洲国家队,分成三个类别
# 只有历年的统计数据,没有目标值(类别,等级)
data = pd.read_csv('./AsiaFootball.txt')# 执行多次,分类结果会有所不同
kmeans = KMeans(n_clusters=3) # n_clusters 分类数量
# 无监督,只需要给数据X就可以
kmeans.fit(data.iloc[:,1:])
y_ = kmeans.predict(data.iloc[:,1:])# 聚类算法预测、划分的类别
c = data['国家'].values
for i in range(3):cond = y_ == i#索引条件print('类别是%d的国家有:'%(i),c[cond])2.6、Kmeans聚类算法K值选择
针对某个样本的轮廓系数s为:
- a:某个样本与其所在簇内其他样本的平均距离
- b:某个样本与其他簇样本的平均距离
聚类总的轮廓系数SC为:,所有样本的
的均值称为聚类结果的轮廓系数,是该聚类是否合理、有效的度量。
import numpy as np
from sklearn import datasets
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# 聚类:轮廓系数,对聚类的评价指标,对应数学公式
from sklearn.metrics import silhouette_score# 创建数据
# 假数据,数据X划分成3类
X,y = datasets.make_blobs(centers=3)
plt.scatter(X[:,0],X[:,1],c = y)# 指定不同的k,寻找最佳聚类类别数目
# 可以画图,一目了然,数据简单,属性只有两个,所以可以画图
# 属性多,无法可视化,评价指标
# 轮廓系数
plt.rcParams['font.sans-serif'] = 'KaiTi'
plt.rcParams['font.size'] = 18
plt.rcParams['axes.unicode_minus'] = False
score = []
for i in range(2,7):kmeans = KMeans(n_clusters=i)kmeans.fit(X)y_ = kmeans.predict(X)# 预测类别 == 标签
# plt.scatter(X[:,0],X[:,1],c = y_)score.append(silhouette_score(X,y_))
# print('当聚类类别是6的时候,评价指标轮廓系数: ',silhouette_score(X,y_))
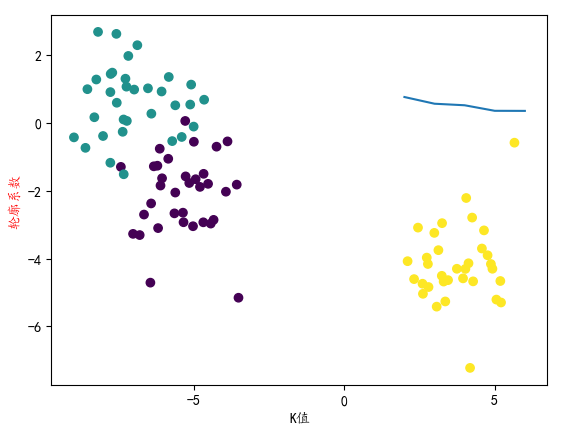
plt.plot(range(2,7),score)
plt.xlabel('K值')
plt.ylabel('轮廓系数',c = 'red')
# 结论:,当k值是3的时候,轮廓系数最大,这个时候,说明划分效果最好!
2.7、Kmeans图像压缩
import matplotlib.pyplot as plt # plt 用于显示图片
from sklearn.cluster import KMeans
import numpy as np
plt.figure(figsize=(8,4))# 加载图片显示原图
pixel = plt.imread('11-bird.png')
plt.subplot(1,2,1)
plt.imshow(pixel)# 聚类运算,压缩图片
pixel = pixel.reshape((128*128 , 3))
kmeans = KMeans(n_clusters=8).fit(pixel)# 聚类结果合成新图片
newPixel = kmeans.cluster_centers_[kmeans.labels_].reshape(128,128,3)
plt.subplot(1,2,2)
plt.imshow(newPixel)
3、DBSCAN
3.1、算法介绍
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇,它将簇定义为密度相连的点的最大集合。
基于密度这点有什么好处呢,我们知道Kmeans聚类算法只能处理球形的簇,也就是一个聚成实心的团(这是因为算法本身计算平均距离的局限)。但往往现实中还会有各种形状,这个时候,那些传统的聚类算法显然就悲剧了。于是就思考,样本密度大的成一类呗。这就是DBSCAN聚类算法 .
3.2、DBSCAN参数解析
- 参数一 eps:DBSCAN算法参数,即我们的eps邻域的距离阈值,和样本距离超过eps的样本点不在eps邻域内。默认值是0.5,一般需要通过在多组值里面选择一个合适的阈值。eps过大,则更多的点会落在核心对象的eps邻域,此时我们的类别数可能会减少, 本来不应该是一类的样本也会被划为一类。反之则类别数可能会增大,本来是一类的样本却被划分开。
- 参数二 min_samples:DBSCAN算法参数,即样本点要成为核心对象所需要的eps 邻域的样本数阈值。默认值是5。
- 参数与三 metrics:距离度量参数, 一般使用的欧氏距离。
3.3、DBSCAN使用示例
import numpy as np
from sklearn import datasets
from sklearn.cluster import KMeans,DBSCAN
import matplotlib.pyplot as plt# y中是两类:0,1
X,y = datasets.make_circles(n_samples=1000,noise=0.05,factor = 0.5)
# 创建一个大圆包含小圆的样本集
# centers = [(1.5,1.5)] 元组,代表着,中心点的坐标值
# y1一类:0 + 2
X1,y1 = datasets.make_blobs(n_samples=500,n_features=2,centers=[(1.5,1.5)],cluster_std=0.2)# 将circle和散点进行了数据合并
X = np.concatenate([X,X1])
y = np.concatenate([y,y1 + 2])
plt.scatter(X[:,0],X[:,1],c = y)# 根据距离,划分‘势力范围’
kmeans = KMeans(3)
kmeans.fit(X)
y_ = kmeans.labels_
plt.scatter(X[:,0],X[:,1],c = y_)# 使用DBSCAN算法可以较好的区分
dbscan = DBSCAN(eps = 0.2,min_samples=3)
dbscan.fit(X)
y_ = dbscan.labels_
plt.scatter(X[:,0],X[:,1],c = y_)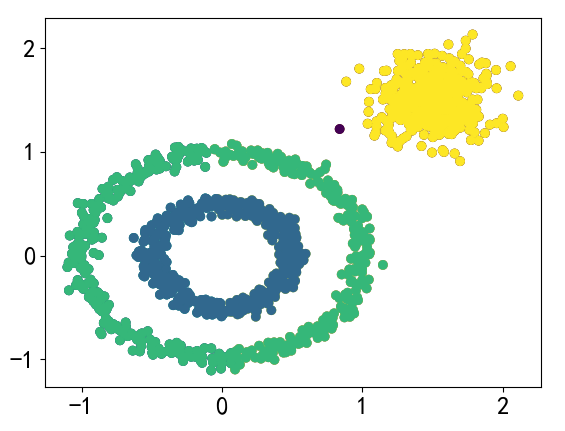
4、分层聚类
4.1、算法介绍
分层聚类输出层次结构,这种结构比平面聚类返回的非结构化聚类集更具信息性。
分层聚类法(hierarchical cluster method)一译“系统聚类法”。聚类分析的一种方法。其做法是开始时把每个样品作为一类,然后把最靠近的样品(即距离最小的群品)首先聚为小类,再将已聚合的小类按其类间距离再合并,不断继续下去,最后把一切子类都聚合到一个大类。
4.2、算法原理
层次聚类 (Hierarchical Clustering) 是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法。
我们着重看一下自底向上的合并算法:
- Single Linkage: 方法是将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这种方法容易受到极端值的影响。两个很相似的组合数据点可能由于其中的某个极端的数据点距离较近而组合在一起。
- Complete Linkage: complete Linkage的计算方法与Single Linkage相反,将两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离。Complete Linkage的问题也与Single Linkage相反,两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起。
- Average Linkage: Average Linkage的计算方法是计算两个组合数据点中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大,但结果比前两种方法更合理。 我们使用Average Linkage计算组合数据点间的距离。下面是计算组合数据点(A,F)到(B,C)的距离,这里分别计算了(A,F)和(B,C)两两间距离的均值。
4.3、参数介绍
- n_clusters: 划分类别数目
- linkage: 度量两个子类的相似度时所依据的距离
- Single Linkage:将两个数据点集中距离最近的两个数据点的距离作为两个点集的距离。
- Complete Linkage:将两个点集中距离最远的两个数据点的距离作为这两个点集的距离。
- 上述两种方法容易受到极端值的影响,计算大样本集效率较高。
- Average Linkage:计算两个点集中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个点集间的距离。这种方法计算量比较大,不过这种度量方法更合理。
- Ward:最小化簇内方差。
- connectivity: 连接性约束,作用:只有相邻的簇才能合并在一起,进行聚类!
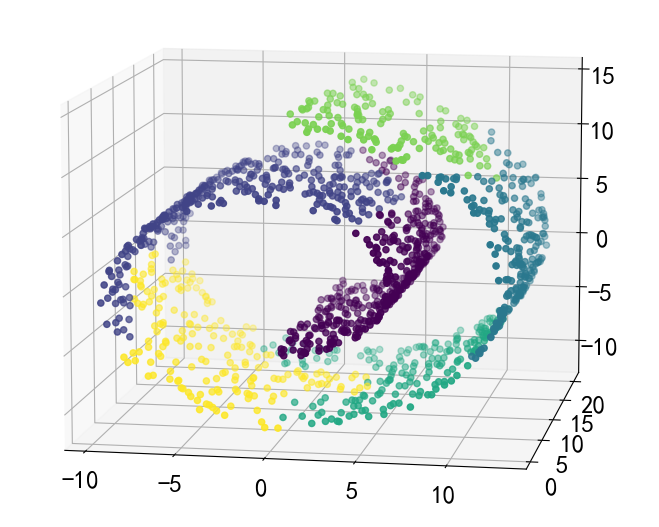
4.4、算法案例
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as p3
from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_swiss_roll# 创建数据
X,y = datasets.make_swiss_roll(n_samples=1500,noise = 0.05)
fig = plt.figure(figsize=(12,9))
a3 = fig.add_subplot(projection = '3d')
a3.scatter(X[:,0],X[:,1],X[:,2],c = y)
a3.view_init(10,-80)# Kmeans只负责分类,随机性,类别是数字几,不固定
clf = KMeans(n_clusters=6)
clf.fit(X)
y_ = clf.labels_
fig = plt.figure(figsize=(12,9))
a3 = plt.subplot(projection = '3d')
a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)
a3.view_init(10,-80)# 分层聚类
agg = AgglomerativeClustering(n_clusters=6,linkage='ward') # 最近的距离为标准
agg.fit(X)
y_ = agg.labels_
fig = plt.figure(figsize=(12,9))
a3 = plt.subplot(projection = '3d')
a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)
a3.view_init(10,-80)
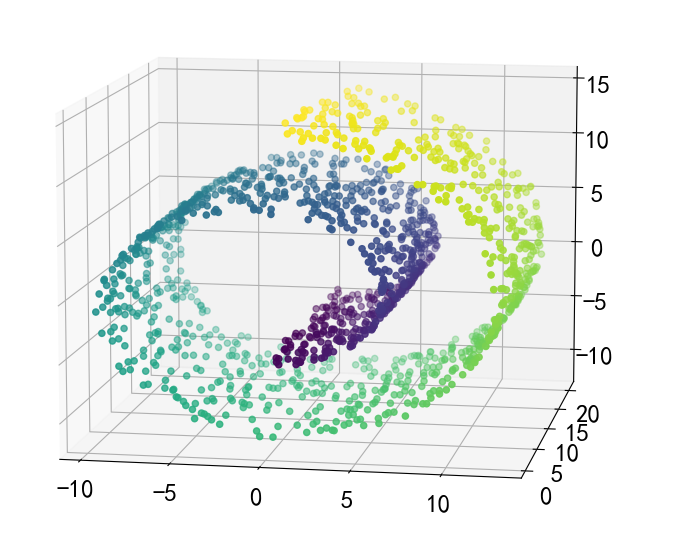
对于这种非欧几何的数据下,可见如果没有设置连接性约束,将会忽视其数据本身的结构,强制在欧式空间下聚类,于是很容易形成了上图这种跨越流形的不同褶皱。
5、分层聚类改进
(连接性约束,对局部结构进行约束)
from sklearn.neighbors import kneighbors_graph# graph图形的意思
# 邻居数量变少,认为,条件宽松
conn = kneighbors_graph(X,n_neighbors=10) #采用邻居,进行约束
agg = AgglomerativeClustering(n_clusters=6,connectivity=conn,linkage='ward')
# 最近的距离,作为标准
agg.fit(X)
y_ = agg.labels_
fig = plt.figure(figsize=(12,9))
a3 = fig.add_subplot(projection = '3d')
a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)
a3.view_init(10,-80)
相关文章:

11- 聚类算法 (KMeans/DBSCAN/agg) (机器学习)
聚类算法 聚类算法和降维算法那都属于无监督算法。KMeans 是以一个值为中心, 然后所有其他点到该点距离最小值的累积和。 kmeans KMeans(n_clusters3) # n_clusters 分类数量 kmeans.fit(data.iloc[:,1:]) # 无监督,只需要给数据X就可以 DBSCAN 算法是…...

日日顺供应链|想要看清供应链发展趋势,先回答这三个问题
技术变革如何支撑供应链及管理服务的发展? 数字化与科技化开始承托供应链管理能力的升级与变革? 如何从客户需求的纬度反推供应链及管理服务的模式变革?在过去的三年中,我国的供应链企业经受了最为极端的挑战,但当下&a…...

5守护进程与线程
进程组 多个进程的集合,第一个进程就是组长,组长进程的PID等于进程组ID。 进程组生存期:进程组创建到最后一个进程离开(终止或转移到另一个进程组)。与组长进程是否终止无关。 一个进程可以为自己或子进程设置进程组 ID 相关函数 pid_t …...
EZ-Cube简易款下载器烧写使用方法
一、硬件连接 跟目标芯片接4根线 VCC、GND、TOOL、REST 四根线,如果板子芯片自己外接电源的,VCC 线可以不接。 二、 安装烧写软件和驱动 烧写软件:https://download.csdn.net/download/Stark_/87444744?spm1001.2014.3001.5503 驱动程序&a…...
sql server安装并SSMS连接
博主简介:原互联网大厂tencent员工,网安巨头Venustech员工,阿里云开发社区专家博主,微信公众号java基础笔记优质创作者,csdn优质创作博主,创业者,知识共享者,欢迎关注,点赞ÿ…...

Python_pytorch (二)
python_pytorch 小土堆pytotch学习视频链接 from的是一个个的包(package) import 的是一个个的py文件(file.py) 所使用的一般是文件中的类(.class) 第一步实例化所使用的类,然后调用类中的方法(def) Torchvision 数据集 数据集使用(CI…...
java手机短信验证,并存入redis中,验证码时效5分钟
目录 1、注册发送短信账号一个账号 2、打开虚拟机,将redis服务端打开 3、创建springboot工程,导入相关依赖 4、写yml配置 5、创建controller层,并创建controller类 6、创建service层,并创建service类 7、创建工具类&#x…...

kubectl命令控制远程k8s集群(Windows系统、Ubuntu系统、Centos系统)
文章目录1. 本地是linux2. 本地是Windows1. 本地是linux 安装kubectl命令 法一:从master的/usr/bin目录下拷贝kubectl文件到本机/usr/bin目录下法二:GitHub下载kubectl文件 在家目录下创建.kube目录config文件 法一:将master上对应用户的~/.…...
【求解器-COPT】COPT的版本更新中,老版本不能覆盖的问题
【求解器-COPT】COPT的版本更新中,老版本不能覆盖的问题方法1方法2如果license还是找不到作者:刘兴禄 参考网址: COPT的下载和配置步骤如下: 教程 | Windows系统下如何安装COPT求解器并配置许可文件: https://zhuan…...
Vue3.0文档整理:一、简介
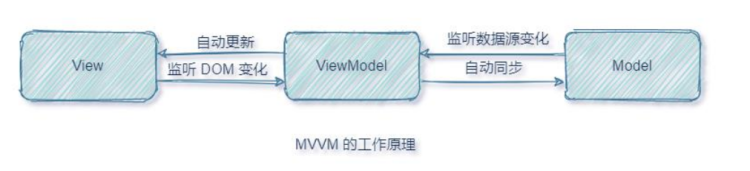
1.1:什么是vue? Vue是一款用于构建用户界面的javascript框架;它基于标准HTML、CSS和Javascript构建,并提供了一套声明式、组件化的编程模型,帮助你高效的开发用户界面。 1.2:MVVM工作原理 MVVM指的是model、view和vie…...
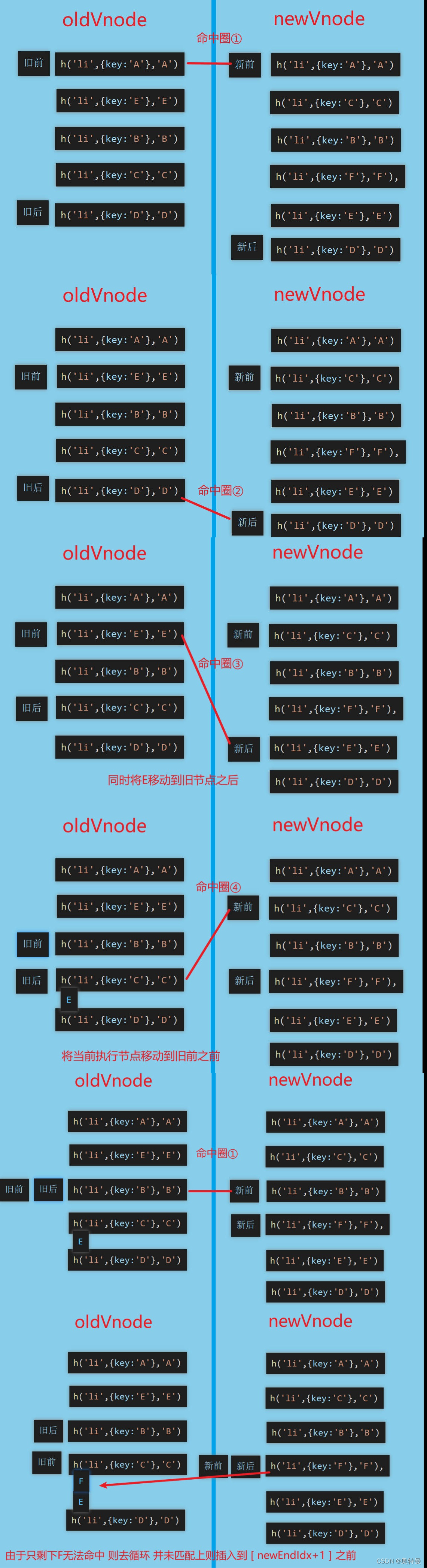
vue2 diff算法及虚拟DOM
概括:diff算法,虚拟DOM中采用的算法,把树形结构按照层级分解,只比较同级元素,不同层级的节点只有创建和删除操作。 一、虚拟DOM (1) 什么是虚拟DOM? 虚拟 DOM (Virtual DOM,简称 VDOM) 是一种…...

Ray和极客们的创新之作,2月18日来发现
所在论坛:数据库技术创新&云原生论坛分享时段:2.18 10:30-11:00分享主题:云原生数据库PieCloudDB :Unbreakable安全特性剖析分享嘉宾:王淏舟,拓数派资深研发工程师 由中国开源软件推进联盟PostgreSQL分…...

Dubbo 源码分析 – 集群容错之 Router
1. 简介 上一篇文章分析了集群容错的第一部分 – 服务目录 Directory。服务目录在刷新 Invoker 列表的过程中,会通过 Router 进行服务路由。上一篇文章关于服务路由相关逻辑没有细致分析,一笔带过了,本篇文章将对此进行详细的分析。首先&…...

行人检测(人体检测)3:Android实现人体检测(含源码,可实时人体检测)
行人检测(人体检测)3:Android实现人体检测(含源码,可实时人体检测) 目录 行人检测(人体检测)3:Android实现人体检测(含源码,可实时人体检测) 1. 前言 2. 人体检测数据集说明 3. 基于YOLOv5的人体检测模型训练 4.人体检测模型…...
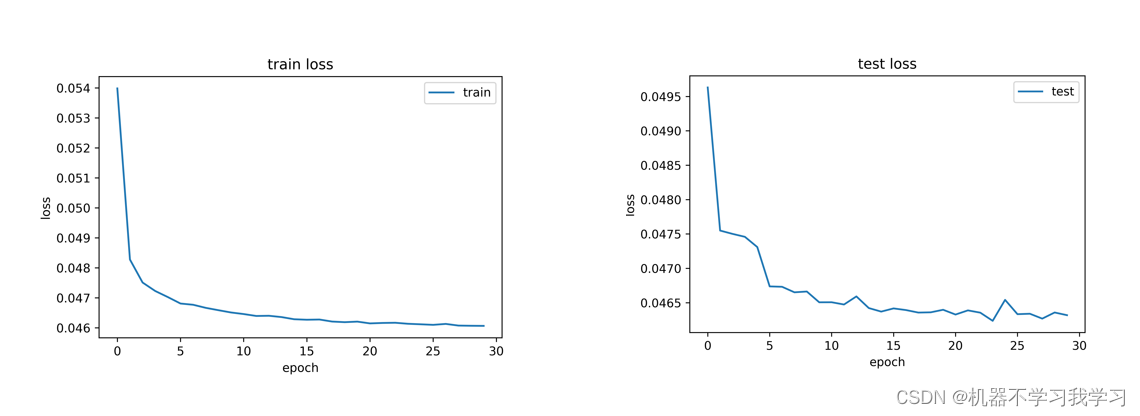
【图像分类】基于PyTorch搭建LSTM实现MNIST手写数字体识别(单向LSTM,附完整代码和数据集)
写在前面: 首先感谢兄弟们的关注和订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 提起LSTM大家第一反应是在NLP的数据集上比较常见,不过在图片分类中,它同样也可以使用。我们以比较熟悉的 mnist…...

Kotlin 1.8.0 现已发布,有那些新特性?
文章目录**如何安装 Kotlin 1.8.0****如果您遇到任何问题****更多文章和视频**结语Kotlin 1.8.0 版本现已发布,以下是其部分最大亮点: JVM 的新实验性功能:递归复制或删除目录内容提升了 kotlin-reflect 性能新的-Xdebug编译器选项ÿ…...

likeshop单商户SaaS商城系统—无限多开,搭建多个商城
likeshop单商户SaaS商城系统:适用于多开(SaaS)、B2C、单商户、自营商城场景,完美契合私域流量变现闭环交易使用,系统拥有丰富的营销玩法,强大的分销能力,支持DIY多模板,前后端分离。…...
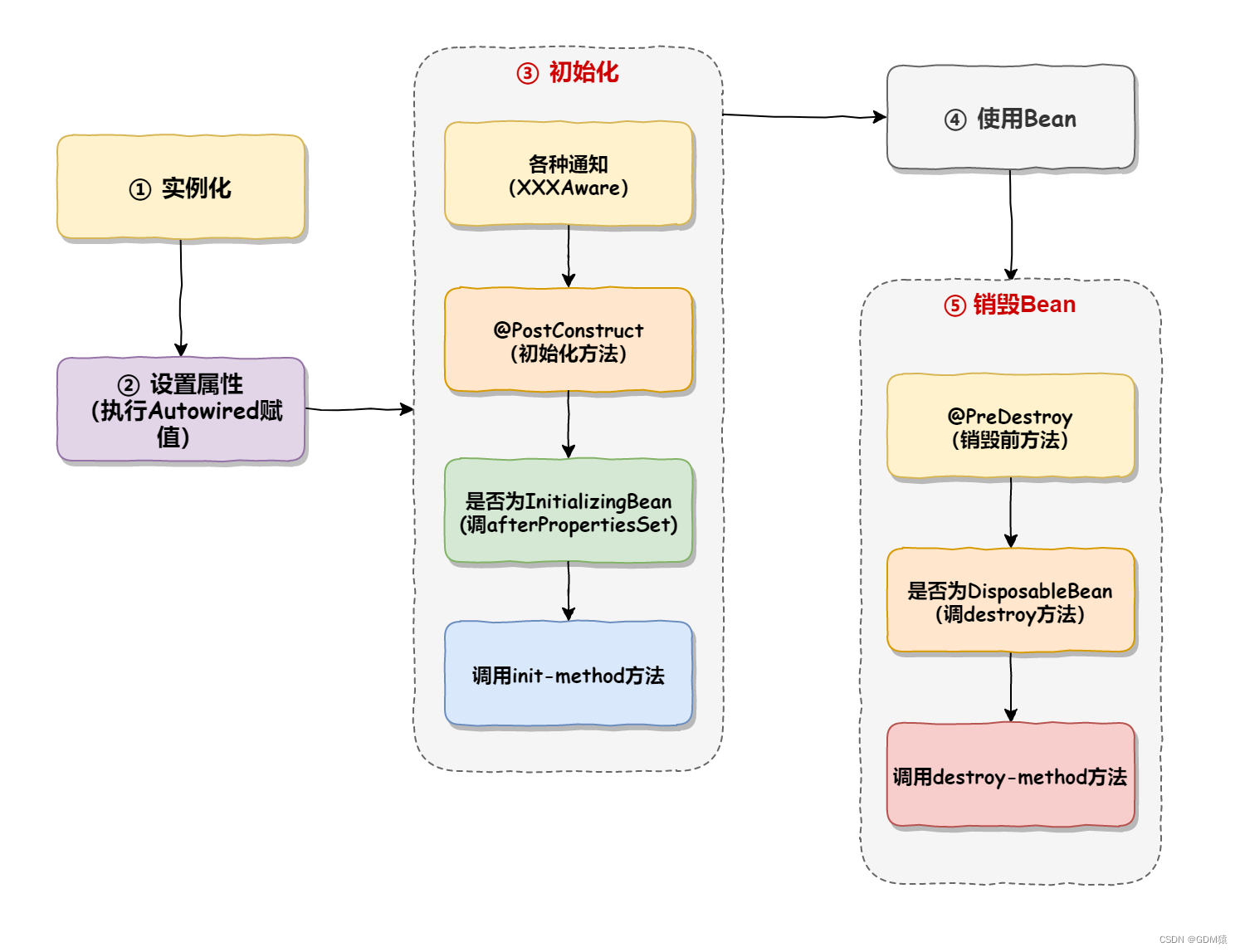
Bean(Spring)的执行流程和生命周期
Bean(Spring)的执行流程具体的流程就和我们创建Spring基本相似。启动 Spring 容器 -> 实例化 Bean(分配内存空间,从无到有) -> Bean 注册到 Spring 中(存操作) -> 将 Bean 装配到需要的…...
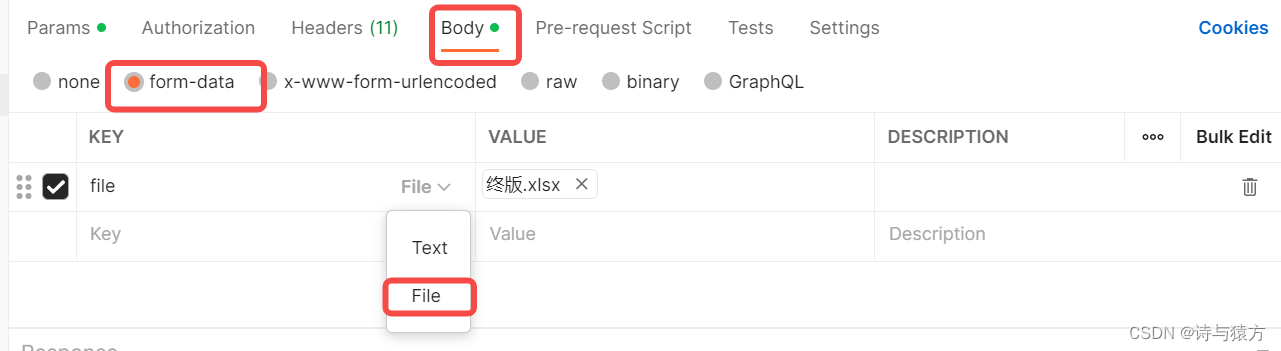
工作记录------PostMan自测文件导入、导出功能
工作记录------PostMan自测文件导入、导出功能 测试文件导出 背景:写了一个文件下载功能,是数据写到excel中,下载,使用PostMan点击send后,返回报文是乱码。 解决办法: 点击send下面的 send and Downlo…...
上海亚商投顾:沪指震荡上行 大消费板块全线走强
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。市场情绪三大指数今日震荡反弹,沪指全天低开高走,深成指、创业板指均涨超1%。工程机械板块集体大涨&a…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
