【动态规划篇】欣赏概率论与镜像法融合下,别出心裁探索解答括号序列问题
 本篇鸡汤:没有人能替你承受痛苦,也没有人能拿走你的坚强.
本篇鸡汤:没有人能替你承受痛苦,也没有人能拿走你的坚强.
欢迎拜访:羑悻的小杀马特.-CSDN博客
本篇主题:带你解答洛谷的括号序列问题(绝对巧解)
制作日期:
2025.01.10隶属专栏:C/C++题海汇总


目录
本篇简介:
一·题目介绍:
二·思路叙述:
2.1判断独立性:
2.2空隙法及填充gap表:
2.3填充dp表:
2.3.1dp状态方程规定:
2.3.2dp的状态转移方程推导及填充:
2.4·镜像法:
2.5细节处理:
三·代码汇总:
四.个人小结:
本篇简介:
本篇主体还是动态规划,之前篇介绍了对它的讲解概念,因此本篇就不做多解释,下面就是利用动态规划,结合概率论推导独立性公式,两步走,并采用镜像法优化一下,最后动态规划得到答案后,采用独立性求积方法得出答案。
一·题目介绍:

洛谷链接: [蓝桥杯 2021 省 AB] 括号序列 - 洛谷
测试用例:
输入:((()
输出:5
二·思路叙述:
当我们看到了括号填充类似问题,是不是想到了leetcode的有道括号生成问题,看着好像:

链接:LCR 085. 括号生成 - 力扣(LeetCode)
下面我们展示下leetcode的代码:
//思路:对于返回的字符串组合,可以考虑是否是决策树的叶子然后用决策树+dfs:即根据n也就是判断递归条件(剪枝)左右支为'('')'它们的选择,
//然后画出决策树分析递归条件,完成dfs设计class Solution {
public://全局变量的设计:int left=0;int right=0;string path;vector<string> ret;vector<string> generateParenthesis(int n) {dfs(n);return ret;}void dfs(int &n){//递归出口:if(path.size()==2*n){ret.emplace_back(path);return;}//判断进入递归的条件(剪枝逆向):if(left<n){path+='(';left++;dfs(n);path.pop_back();left--;//回溯}if(right<left){path+=')';right++;dfs(n);path.pop_back();right--;//回溯}}
};但是我们仔细一下看,本题并不是自己生成所有种类的正确情况,而是让我们自己在它给例子去填充让它有效。

看到这里,根据我们上一篇的经验就很容易想到动态规划去解答,因此leetcode上面深度优先遍历的方法就寄掉了。
因此下面我们就用动态规划思想去解答;但是它也是不好想到;甚至我们去看题解,是不是都看不懂比如:


这里可以看出要么就是三层for嵌套循环填dp,以及很多人会发现题解甚至都看不懂,即便看懂还要琢磨很久才会明白(当然这里博主也是);因此博主在这出一篇文章来解释一下,让大家可以更加明白这道题是如何解答的。
那么下面我们就以题目给的例子来畅谈:
2.1判断独立性:
首先,我们的任务就是要么填充右括号来干掉左括号,要么填充左括号来干掉右括号;反正就是要得到这样以最小的添加括号让它合法的添加方法数;那么下面我们说一下结论:
这里可以知道添加右括号使它合法(也就是利用右括号干掉左括号)的方法数和添加左括号方法数是独立的---->而题目要求是添加左括号和右括号是都行的,因此最后就可以转化成添加左括号方案数与右括号方案数之积(两者是独立的) 。
证明:
这里为什么可以得到上面说的结论,直接就把问题简单化,单一化了:
这里需要用到的概率论的公式:
说白了就是A B两个事件如果互不干扰,互不影响,那么此时两种同时发生的概率就是两者单独发生概率之积, 而本题呢?
我们给它的目的简化一下,使得它更贴近这,题目其实就是要求让我们要么补充左括号,要么补充右括号,对应把相反括号干掉,也就是所说的使得左右括号都合法;而我们补充右括号使得左括号合法并没有影响其他右括号的合法性(因为我们没有补充左括号)-->所以左右括号的合法性是独立的。
因此我们可以拆开来分别求它们单独的合法性种类然后求个积就是题目要的使得例子左右括号都合法的种类数。
这里注意下:题目所说最少填充括号的意思就是比如对于((()我们不能无缘无故让添加一对括号让它合法:((()()()()))类似这样。
因此我们可以得到一个公式:
ret=(re_left*re_right)%1e9+7 这里题目要求结果太大要取模
解释一下:也就是我们使左括号合法的种类*使右括号合法的种类。
那么也就是我们怎么求左括号和发的种类:这里我们引入一下空隙法(后面我们得知独立性后就基于判断左括号合法性来讲解)。
2.2空隙法及填充gap表:
这里我们以左括号为例,就是我们每当多一个左括号就相当于多了一个可以填充右括号的空隙;但是当我们遍历到右括号,空隙个数可以理解成没变;但遍历到当前(0~当前空隙)能填充右括号个数要少一个(保证非负性,大于0才减少)
然后就是我们搞一个空隙数组记录的就是前i个空隙中最多可以放多少个括号:gap[i](这里为了方便我们一一对应,因此下标从1开始,对应的是前多少个空隙)
下面我们举个例子吧:
比如:((() :这里有三个空隙,具体变化gap数组的值(随着遍历):1-->2-->3-->2(这注意是吧第三个空隙的最大容量减1)。
再比如:

因为多少个左括号就意味着可以补充多少右括号;但是空隙最大容量也就是补充括号的个数是随着与之反作用的括号相关的
因此下面重点:我们总结一下空隙规则(这里我们都以补充右括号使左括号合法来谈):
①空隙的个数也就是左括号的个数;
②当遇到右括号的话空隙所容纳的括号数就减少(前提是大于0)。
下面就根据上述所讲填充空隙表gap:
l:记录的左括号个数也就是空隙个数
void init_gap() {//填充gap数组,也就是判断多少个空隙以及前多少个空隙的
//最大容量for (int i = 0; i < N; i++) {if (s[i] == '(') {l++;gap[l] = gap[l - 1] + 1;}else gap[l] > 0 ? gap[l]-- : 1;//这里注意当干右括号的时候//因为是求得最少补充的左括号数,故不能出现负}
}但是这里我们就可以得到公式也就是判断填右括号使得左括号合法的规定:
我们gap数组存的都是遍历到当前空隙开始从0~i补充右括号最大个数;因此我们当填充dp表的时候遍历填写括号个数的要加一个判断:
填充括号个数<=gap[遍历到当前的空隙] 即 i<=gap[j]。
那又要问了为什么动态规划不是填充dp表为啥搞个空隙表;因为后面我们会填充dp就是根据多少个空隙(遍历到哪里),最多可以填充多少个括号来填充的故肯定是有用的。
2.3填充dp表:
2.3.1dp状态方程规定:
那么首先我们肯定要先定义dp表的状态:
因为它是遍历到哪里,然后又要在这段区间填充括号(多少个)使它变得合法,因此最好搞一个二维dp表。
那么我们结合上面搞的空隙表,规定状态:
dp[i][j]代表遍历到第j个空隙处,可以在0~i个空隙内可以填充i个括号的种类数(这里我们遍历只按照左括号走)2.3.2dp的状态转移方程推导及填充:
这里由于让下标与实际意义对应及可能会出现状态方程自己初始化需要前边的值,我们选择多开,并手动初始化。
首先呢对于大多数人直接用脑子按照这个逻辑去想状态方程是啥样,肯定是困难的,因此我们搞一个简单的例子带大家总结一下状态转移方程:

首先我们根据这个例子自己按照dp状态规定填好dp表;但是为什么第一行都填0呢 ?
这就是我们状态方程自己循环填充要用到的,需要我们提前进行初始化:
也就是把0个括号插入到0-l个空隙插入的方案:这里我们可以理解成把0个即插入“空气”这种插法,故只有一种情况(虽然有些勉强);其次就是我们只能根据找规律,细心的话如果我们第一行不填写,可以发现如果都填写1的话可以得到一个公式:
其实就是我们那个填写dp表的一个“1”形状dp值之和;我们可以根据这个公式来往上递推成“/”形状的dp值这样就无需再来一层for循环(就像上面说的o(N^3)一样复杂度的三层for了)只需取前面填充的两个dp值就好了。
如:

因此公式化简(也就是我们填充dp表要用的公式):
当然了后面我们写的时候要对1e9+7取模(题目说明,就不用说了吧,还有就是long long的奇妙之处了)
那dp填表的过程这个公式就ok吗?
当然还会有条件限制,这里我们在填充空隙表gap数组的时候就说了:

加上这个条件后填充dp就ok了。
这个条件就解释了为什么最后填充三个括号为0以及这么多位置填写0的原因了。
最后我们要的是在0~j个空隙能填充的最大括号数的方案数(遍历到对应空隙,此空隙里面放的gap数组值)即:
dp[gap[l]][l];这样我们就得到了上面所说的re_left值了(记住也是long long) 。
后面我们在去求re_right难道也是写一个类似的两个函数去完成吗?
当然不用了,直接给他镜像一下,就等同于判断左括号的合法性了;这也就是本篇标题提到的镜像法的巧妙了。
2.4·镜像法:
这里虽然名字起的多好高级,其实并不难理解,之所以这么操作就是为了让我们不用再多写函数就可以完成对右括号像左括号一样类似的检验;所以为什么起这个名字呢,下面看张图片:

这样就可以看出了我们要检查右括号的合法性(补充左括号);其实就是把它镜像一下然后再检验一次左括号的合法性就行了。
其实也不难操作:就是遍历一下原串,把左括号改成右括号,右括号改成左括号;然后再利用迭代器逆置一下就好
最后我们根据独立性返回两者之积就好了(但是注意范围long long ,其次就是取模)。
2.5细节处理:
也就是分享一下博主在写这道题遇到的困难,即一些细节问题没注意到而导致的:
比如:
①博主写的代码这里大都用的全局变量(好处就是可以让函数不用传参,坏处就是如果再次使用就要重新初始化)
l=0;//再次填充gap是需要对它初始化0memset(dp,0,sizeof(dp));//再次用填充dp表也要对它初始化0②就是结果要是long long类型否则即不能通过(比如和dp值有关都要是long long,最后答案等);否则就这样:

这就是re_left和re_right没有long long的结果;果真映射那句话:“不加long long 见祖宗” 。
③其次就是那些细节问题,比如填充gap表注意:

填充dp表要注意:

这样细节都处理好就大差不大了。
三·代码汇总:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#define MAX 1000000007
#define C 5000
ll dp[C+1][C + 1] = { 0 };//表示把i个括号插入到前j个空隙的方案数
int gap[C + 1] = { 0 };//下标是第几个空隙,值是空隙的最大左括号容量
string s;
int N;
int l=0;//记录左括号数量
void init_gap() {//填充gap数组,也就是判断多少个空隙以及前多少个空隙的
//最大容量for (int i = 0; i < N; i++) {if (s[i] == '(') {l++;gap[l] = gap[l - 1] + 1;}else gap[l] > 0 ? gap[l]-- : 1;//这里注意当干右括号的时候//因为是求得最少补充的左括号数,故不能出现负}
}
ll get_ans() {for (int i = 0; i <= l; i++) dp[0][i] = 1;for (int i = 1; i <= l; i++) {for (int j = 1; j <= l; j++) dp[i][j] = gap[j] >= i ? (dp[i - 1][j] + dp[i][j - 1]) % MAX:0;//填充的括号数量不能超过前多少个空隙所能容下的最大 }return dp[gap[l]][l];//输出的是把最大空隙数所能容的括号数填入的最多方式数
}
void mapping_r_to_l(){//补充左括号干掉右括号转化成补充右括号干掉左:
//镜像一下子,使得写的干左括号的函数还可以用reverse(s.begin(), s.end());for (int i = 0; i < N; i++)s[i] =(s[i] == '(' ? ')' : '(');
}
int main() {cin >> s;N = s.size();init_gap();ll re_left = get_ans();mapping_r_to_l();l=0;//全局劣势init_gap();memset(dp,0,sizeof(dp));//全局劣势ll re_right = get_ans();cout << (re_left * re_right) % MAX << endl;//利用独立性return 0;} 最后也是满分AC了:

四.个人小结:
这里对于动态规划的题型做法就不总结了,因为上篇总结过啦,具体可看:【动态规划篇】步步带你深入解答成功AC最优包含问题(通俗易懂版)-CSDN博客
此外就是对于不熟悉的题目,我们要对看看题解,看看大佬们是用什么奇妙的方法解答的,当然可能会看不懂,但是我们不要放弃,一天看不懂就多看几天,只要愿意学习别人的解法,总是会可以悟懂的(这里说一下博主写这篇文章其实也是学习了大佬的写法,当然也是看了好几天),所以我们自己不熟练就要多多学习必然的解法做好总结,尽最大可能去吸收它。这里博主建议如果看题解看不懂,尽量找写的比较详细的博客去学习(博主自荐一下:可以参考向博主这样写的文章去看,去学习,如有不足,指出来博主会尽力修改)
还是那句话,只要愿意学肯定能学会的,关键还是在于你的抉择。
对此,我之所以能写出这篇文章还要感谢一位博主写的它的文章,通过阅读,揣摩那位博主的文章;加上自己的理解才可创作出这篇文章(相当于对那位博主的文章的深刻解释以及加上了自己的理解吧)
借鉴的博主文章链接:第十二届蓝桥杯B组省赛括号序列题解_蓝桥杯判断括号合法-CSDN博客
当然还是先建议把博主的文章读懂再去读这位博主的文章,毕竟个人认为自己的文章对它解释了很多地方,更方便读者阅读。

感谢大家阅读!!!
相关文章:

【动态规划篇】欣赏概率论与镜像法融合下,别出心裁探索解答括号序列问题
本篇鸡汤:没有人能替你承受痛苦,也没有人能拿走你的坚强. 欢迎拜访:羑悻的小杀马特.-CSDN博客 本篇主题:带你解答洛谷的括号序列问题(绝对巧解) 制作日期:2025.01.10 隶属专栏:C/C题…...
Java(day7)
字符串练习 生成验证码 package day6; /*生成验证码 内容:可以是小写字母,也可以是大写字,还可以是数字 规则: 长度为5 内容中是四位字母,1位数字。 其中数字只有1位,但是可以出现在任意的位置。*/ impor…...

Word 转成pdf及打印的开源方案支持xp
Word转成pdf、打印的方案几乎没有免费开源的方案,现在提供一个通过LibreOffice实现的方案 操作依赖LibreOffice需要安装,点此下载老版本 5.4.7.2是最后一个支持xp的 版本如需xp要请安装此版本 LibreOffice官方介绍 LibreOffice 是一款开放源代码的自…...

LabVIEW软件侵权分析与应对
问:如果涉及到LabVIEW软件的仿制或模仿,特别是在功能、界面等方面,如何判断是否构成侵权?该如何应对? 答:LabVIEW软件的侵权问题,尤其是在涉及到仿制或模仿其功能、界面、设计等方面࿰…...

【redis】centos7下安装redis7
在CentOS 7下安装Redis7可以通过以下两种方法实现:手动编译安装和使用YUM进行安装。 CentOS 7系统的环境和版本: $ cat /etc/centos-release CentOS Linux release 7.9.2009 (Core)手动编译安装 参考官方文档:https://redis.io/docs/lates…...
)
[network]回顾:集线器(Hub)
集线器(Hub)的发明是计算机网络发展史上的一个重要里程碑。它最初的设计目的是为了解决局域网(LAN)中多台计算机共享网络资源的需求。 #mermaid-svg-OAmOmKYGAXoglS5z {font-family:"trebuchet ms",verdana,arial,sans-…...

79 Openssl3.0 RSA公钥加密数据
1 引言 最近不小心用到了openssl3.0,项目中需要使用rsa非对称加解密算法,所以把openssl3.0使用公钥加密数据的函数调用摸了一遍。 之所以记录此篇文章,是因为网络上大多数是openssl3.0以前的版本的函数接口,而openssl3.0之后已经丢…...
)
EFCore HasDefaultValueSql (续2 HasComputedColumnSql)
前情:EFCore HasDefaultValueSql EFCore HasDefaultValueSql (续1 ValueGeneratedOnAdd)-CSDN博客 小伙伴在使用 HasDefaultValueSql 时,对相关的 ValueGeneratedOnAdd, HasComputedColumnSql 也有了疑问: HasComputedColumnSql 对于计算…...
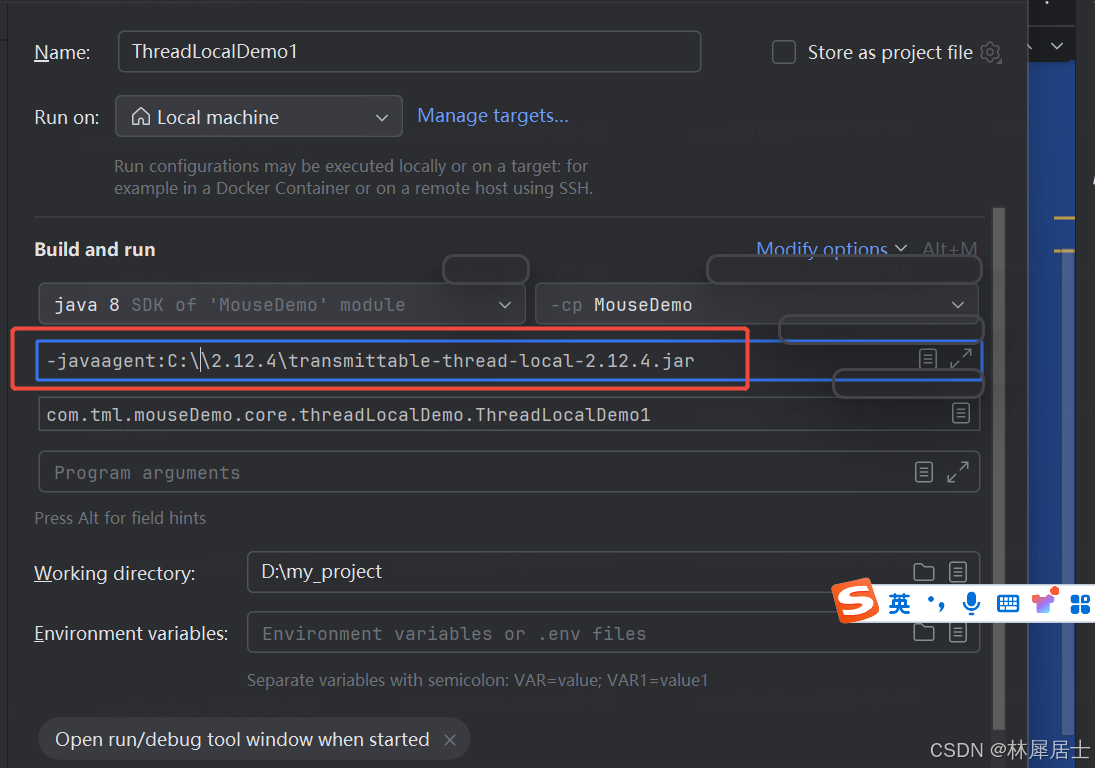
阿里巴巴TransmittableThreadLocal使用指南
前言 ThreadLocal在上下文的数据传输上非常的方便和简洁。工业实践中,比较常用的有三个,ThreadLocal、InheritableThreadLocal、TransmittableThreadLocal,那么他们三个之间有什么区别呢? 常见的三种ThreadLocal比较 ThreadLoc…...
)
ubuntu20下编译linux1.0 (part1)
author: hjjdebug date: 2025年 01月 09日 星期四 15:56:15 CST description: ubuntu20下编译linux1.0 (part1) 该博客记录了新gcc编译旧代码可能碰到的问题和解决办法, 可留作参考 操作环境: ubuntu20 $ gcc --version gcc (Ubuntu 9.4.0-1ubuntu1~20.04.2) 9.4.0 $ as --vers…...

欧拉公式和傅里叶变换
注:英文引文机翻,未校。 中文引文未整理去重,如有异常,请看原文。 Euler’s Formula and Fourier Transform Posted byczxttkl October 7, 2018 Euler’s formula states that e i x cos x i sin x e^{ix} \cos{x} i …...
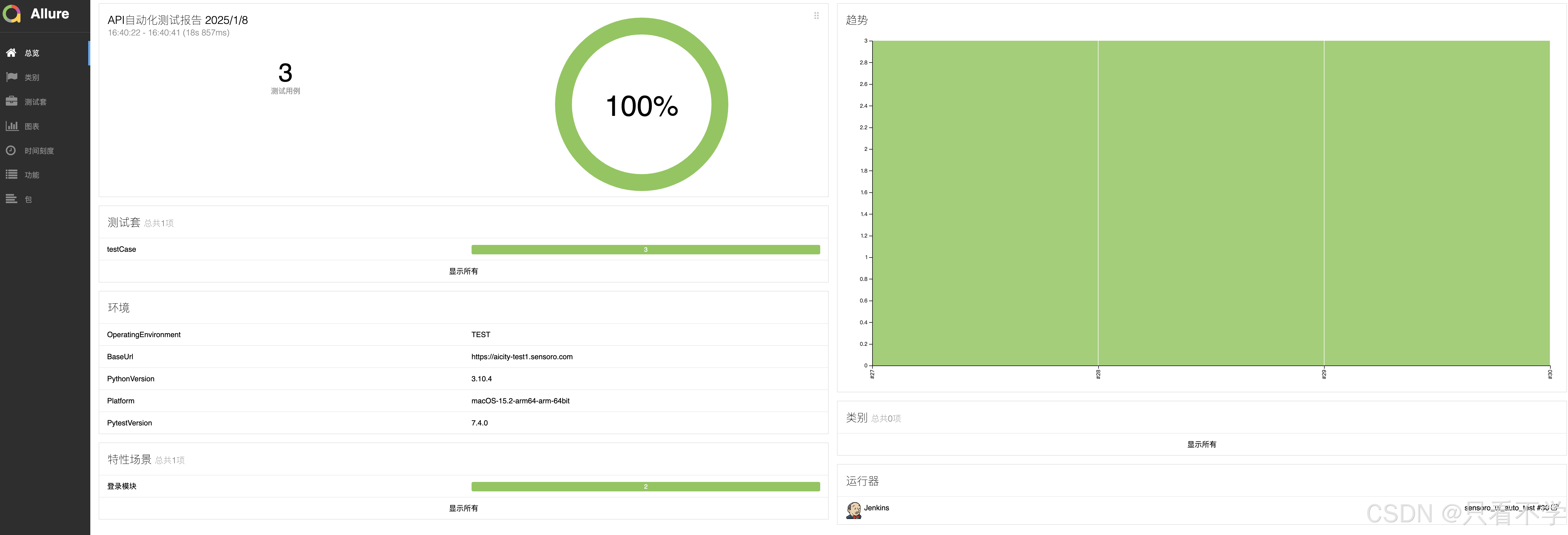
Jenkins内修改allure报告名称
背景: 最近使用Jenkins搭建自动化测试环境时,使用Jenkins的allure插件生成的报告,一直显示默认ALLURE REPORT,想自定义成与项目关联的名称,如图所示,很明显自定义名称显得高大上些,之前…...
30天开发操作系统 第 12 天 -- 定时器 v1.0
前言 定时器(Timer)对于操作系统非常重要。它在原理上却很简单,只是每隔一段时间(比如0.01秒)就发送一个中断信号给CPU。幸亏有了定时器,CPU才不用辛苦地去计量时间。……如果没有定时器会怎么样呢?让我们想象一下吧。 假如CPU看不到定时器而仍想计量时…...

Ubuntu | PostgreSQL | 解决 ERROR: `xmllint` is missing on your system.
解决 sudo apt install apt-file sudo apt-file updatesudo apt-file search xmllint sudo apt install libxml2-utils执行 # postgres源码安装包解压文件夹中 make install make install问题 make -C src install make[2]: Entering directory /home/postgres/postgresql-1…...
uniapp使用chooseLocation安卓篇
本文章全部以高德地图为例 代码 <view class"bottom"><button click"choose">定位</button> </view> choose() {uni.chooseLocation({success: function(res) {console.log(位置名称: res.name);console.log(详细地…...

《PC 上的开源神经网络多模态模型:开启智能交互新时代》
《PC 上的开源神经网络多模态模型:开启智能交互新时代》 一、引言二、多模态模型基础剖析(一)核心概念解读(二)技术架构探秘 三、开源多模态模型的独特魅力(一)开源优势尽显(二&…...
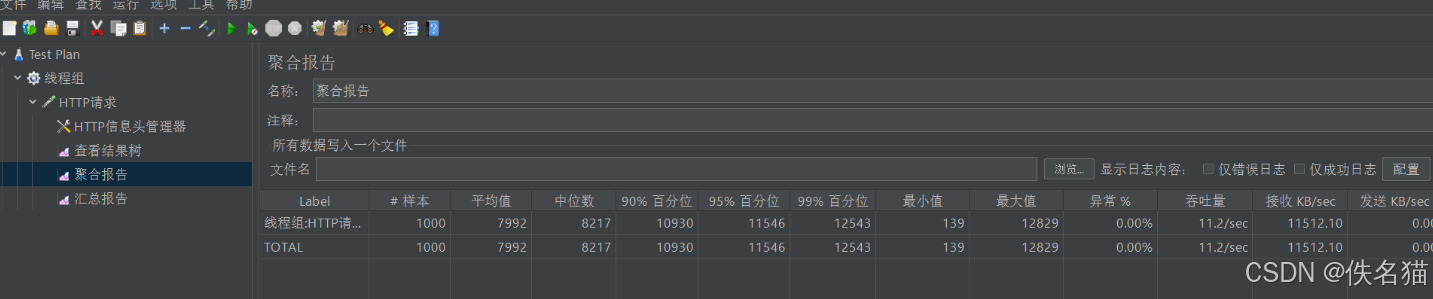
Apache JMeter 压力测试使用说明
文章目录 一、 安装步骤步骤一 下载相关的包步骤二 安装 Jmeter步骤三 设置 Jmeter 工具语言类型为中文 二、使用工具2.1 创建测试任务步骤一 创建线程组步骤二 创建 HTTP 请求 2.2 配置 HTTP 默认参数添加 HTTP消息头管理器HTTP请求默认值 2.3 添加 查看结果监听器2.4 查看结果…...

腾讯云AI代码助手编程挑战赛-知识百科AI
作品简介 知识百科AI这一编程主要用于对于小朋友的探索力的开发,让小朋友在一开始就对学习具有探索精神。在信息化时代下,会主动去学习自己认知以外的知识,同时丰富了眼界,开拓了新的知识。同时催生了在大数据时代下的信息共享化…...

【SpringAOP】Spring AOP 底层逻辑:切点表达式与原理简明阐述
前言 🌟🌟本期讲解关于spring aop的切面表达式和自身实现原理介绍~~~ 🌈感兴趣的小伙伴看一看小编主页:GGBondlctrl-CSDN博客 🔥 你的点赞就是小编不断更新的最大动力 &am…...
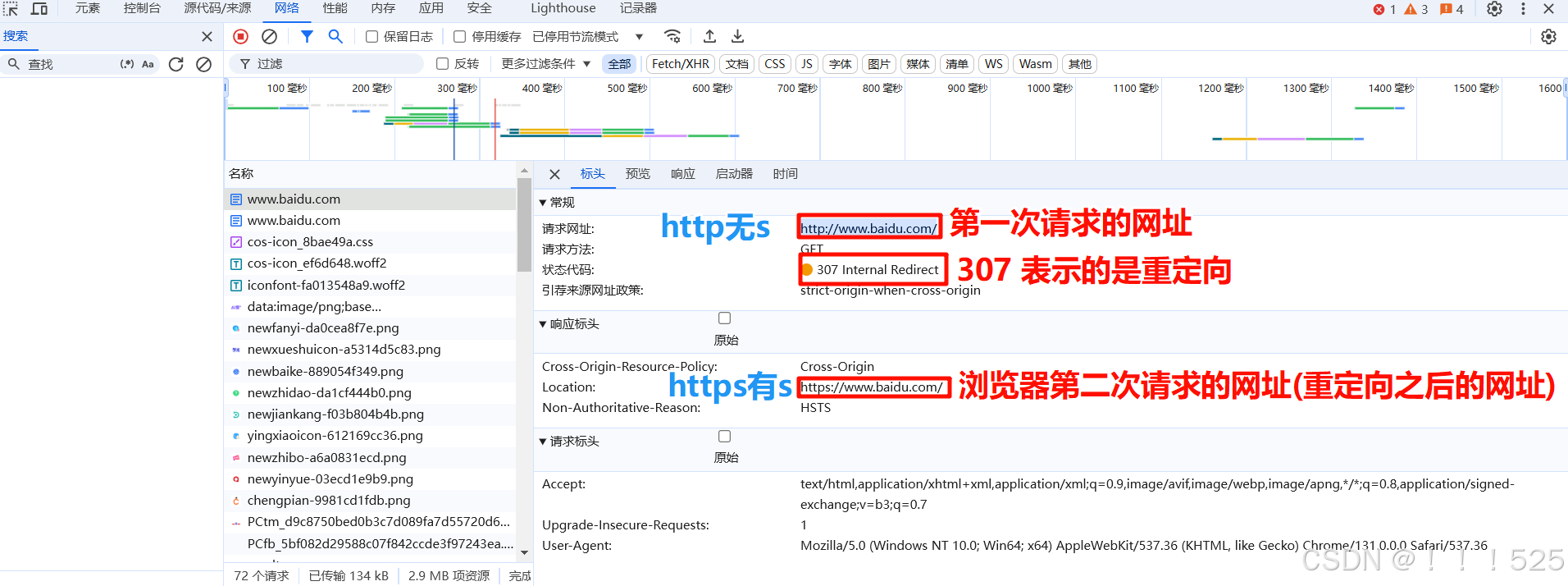
HTTP-响应协议
HTTP的响应过程? 浏览器请求数据--》web服务器过程:请求过程 web服务器将响应数据-》到浏览器:响应过程 响应数据有哪些内容? 1.和请求数据类似。 2. 响应体中存储着web服务器返回给浏览器的响应数据。并且注意响应头和响应体之间…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...
)
零基础在实践中学习网络安全-皮卡丘靶场(第十一期-目录遍历模块)
经过前面几期的内容我们学习了很多网络安全的知识,而这期内容就涉及到了前面的第六期-RCE模块,第七期-File inclusion模块,第八期-Unsafe Filedownload模块。 什么是"遍历"呢:对学过一些开发语言的朋友来说应该知道&…...

【R语言编程——数据调用】
这里写自定义目录标题 可用库及数据集外部数据导入方法查看数据集信息 在R语言中,有多个库支持调用内置数据集或外部数据,包括studentdata等教学或示例数据集。以下是常见的库和方法: 可用库及数据集 openintro库 该库包含多个教学数据集&a…...
