力扣经典二分题:4. 寻找两个正序数组的中位数
题目链接:4. 寻找两个正序数组的中位数 - 力扣(LeetCode)
一、题目分析
- 这道题目是让我们在 两个正序的数组中寻找中位数
- 已知两个数组的大小分别是:int m = nums1.size(),n = nums2.size();
- 中位数性质1:中位数左侧元素 ≤ 中位数 且 中位数右侧元素 ≥ 中位数 (以升序来看)
- 中位数性质2:对于一个长度为
N的数组,中位数将数组一分为二,使得左侧与右侧得元素长度差 ≤ 1 - 当 m + n 为奇数时,我们需要找到合并后数组中第 k + 1 小的元素,其中 k = (m + n) / 2。
- 当 m + n 为偶数时,我们需要找到合并后数组中第 k 和第 k + 1 小的元素,然后计算它们的平均值,其中 k = (m + n) / 2 - 1(注意这里 k 是基于 0 的索引,所以实际要找的元素位置是 k 和 k + 1)。
二、算法原理讲解
解法一:暴力排序
通过合并排序的原理,通过中位数的性质,可快速得到中位数的下标,较为简单
时间复杂度为O(M+N),空间复杂度为O(M+N)
解法二:双指针
时间复杂度为O(M+N),空间复杂度为O(1)
解法三:暴力枚举
解法四:二分优化
三、编写代码
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size(), n = nums2.size();if(m > n) swap(nums1,nums2); // 保证nums1始终是较短数组int k = (m + n + 1) / 2; // 应划分给小数组的个数// 枚举 i [0,m]for(int i = 0;i <= m;i++){int&& j = k - i;// 分割线周围的四个值int a = i == m ? INT_MAX :nums1[i];int b = i == 0 ? INT_MIN :nums1[i-1];cout << i << ' ' << j << endl;int c = j == n ? INT_MAX :nums2[j];int d = j == 0 ? INT_MIN :nums2[j-1];// 分割线是否合法if(b <= c && d <= a){if((m + n) % 2 == 1) return max(b,d);else return (double)(max(b,d) + min(c,a)) / 2;}}return 1314.521;}
};
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {// 保证nums1始终是较短数组if(nums1.size() > nums2.size()) swap(nums1,nums2);// 应划分给小数组的个数int k = (nums1.size() + nums2.size() + 1) / 2; // 枚举nums1数组中应该划分给小数组的元素个数(二分优化)int left = 0,right = nums1.size();while(left < right){// mid ∈ [0,m]int i = (left + right + 1) / 2; int j = k - i;cout << i << endl;if(nums1[i-1] <= nums2[j]) left = i;else right = i - 1;}// 分割线两边的值int a = left == nums1.size() ? INT_MAX :nums1[left];int b = left == 0 ? INT_MIN :nums1[left-1];int c = (k-left) == nums2.size() ? INT_MAX :nums2[k-left];int d = (k-left) == 0 ? INT_MIN :nums2[k-left-1];// 处理数据+返回if((nums1.size() + nums2.size()) % 2 == 1) return max(b,d);else return (double)(max(b,d) + min(c,a)) / 2;}
};
相关文章:

力扣经典二分题:4. 寻找两个正序数组的中位数
题目链接:4. 寻找两个正序数组的中位数 - 力扣(LeetCode) 一、题目分析 这道题目是让我们在 两个正序的数组中寻找中位数已知两个数组的大小分别是:int m nums1.size(),n nums2.size();中位数性质1:中位数左侧元素 …...
解决WordPress出现Fatal error: Uncaught TypeError: ftp_nlist()致命问题
错误背景 WordPress版本:wordpress-6.6.2-zh_CN WooCommerce版本:woocommerce.9.5.1 WordPress在安装了WooCommerce插件后,安装的过程中没有问题,在安装完成后提示: 此站点遇到了致命错误,请查看您站点管理…...
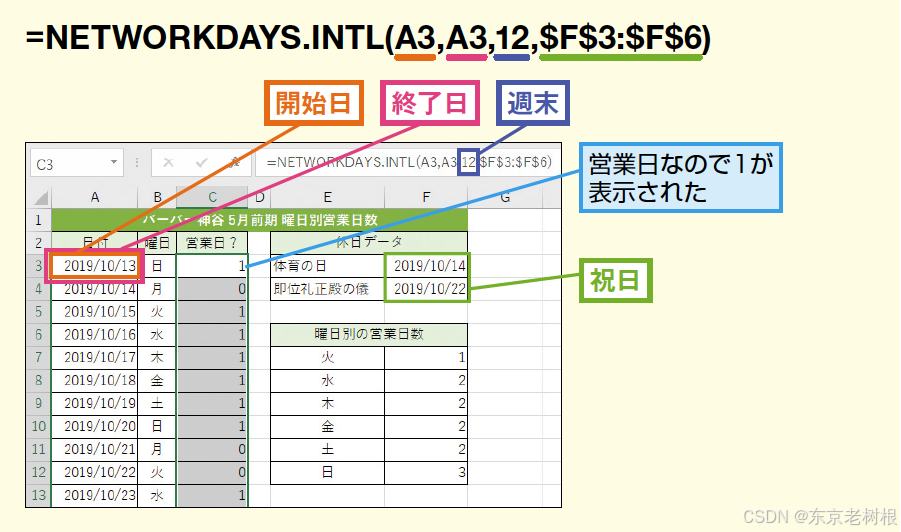
Excel 技巧07 - 如何计算到两个日期之间的工作日数?(★)如何排除节假日计算两个日期之间的工作日数?
本文讲了如何在Excel中计算两个日期之间的工作日数,以及如何排除节假日计算两个日期之间的工作日数。 1,如何计算到两个日期之间的工作日数? 其实就是利用 NETWORKDAYS.INTL 函数 - weekend: 1 - 星期六,星期日 2,如…...

快速实现一个快递物流管理系统:实时更新与状态追踪
物流管理是电商、仓储和配送等行业的重要组成部分。随着电子商务的快速发展,快递物流的高效管理和实时状态更新变得尤为关键。本文将演示如何使用Node.js、Express、MongoDB等技术快速构建一个简单的快递物流管理系统,该系统支持快递订单的实时更新和追踪…...
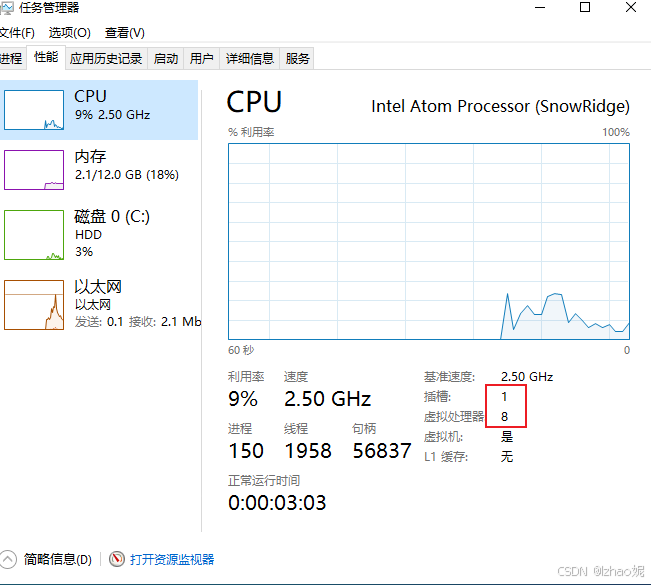
kvm 解决 安装windows 虚拟机cpu 核数问题
通过lscpu命令查到我本机的cpu信息如下 CPU(s): 12 —— 系统的总逻辑处理单元数量(包括所有核心和逻辑处理器)。Thread(s) per core: 2 —— 每个物理核心支持 2 个线程(表示启用了超线程技术)。Core(s) per socket: 6 —— 每个…...
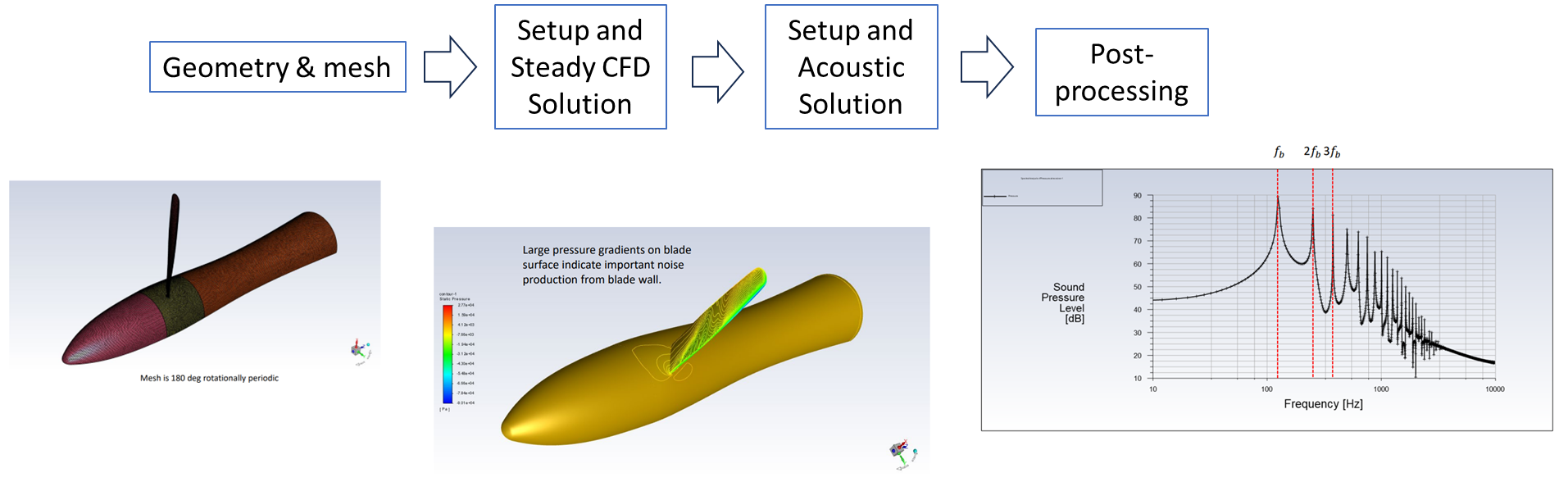
Ansys Fluent Aeroacoustics 应用
探索 Ansys Fluent 在气动声学领域的前沿功能,彻底改变各行各业解决降噪和提高音质的方式。 了解气动声学 气动声学是声学的一个分支,它处理湍流流体运动产生的噪声以及这些声音通过流体介质(如空气)的传播。这个领域在工程中至…...

119.使用AI Agent解决问题:Jenkins build Pipeline时,提示npm ERR! errno FETCH_ERROR
目录 1.Jenkins Build时的错误 2.百度文心快码AI智能体帮我解决 提问1:jenkins中如何配置npm的源 提问2:jenkins pipeline 类型为pipeline script from SCM时,如何配置npm源 3.最终解决方法-Jenkinsfile的修改 4.感触 1.Jenkins Build时…...

istio-proxy内存指标
在 Istio 环境中,istio-proxy 是 Envoy 的边车代理容器。通过运行命令 curl localhost:15000/memory,或者curl localhost:15000/stats 可以查询 Envoy 的内存统计信息。以下是典型返回结果的结构和意义: 返回结果单位是bytes,需/…...

List详解 - 双向链表的操作
在C中,std::list是标准模板库(STL)中的一个容器,它实现了双向链表的数据结构。与数组或向量(std::vector)不同,std::list允许在常数时间内进行插入和删除操作,尤其是在链表的任意位置…...
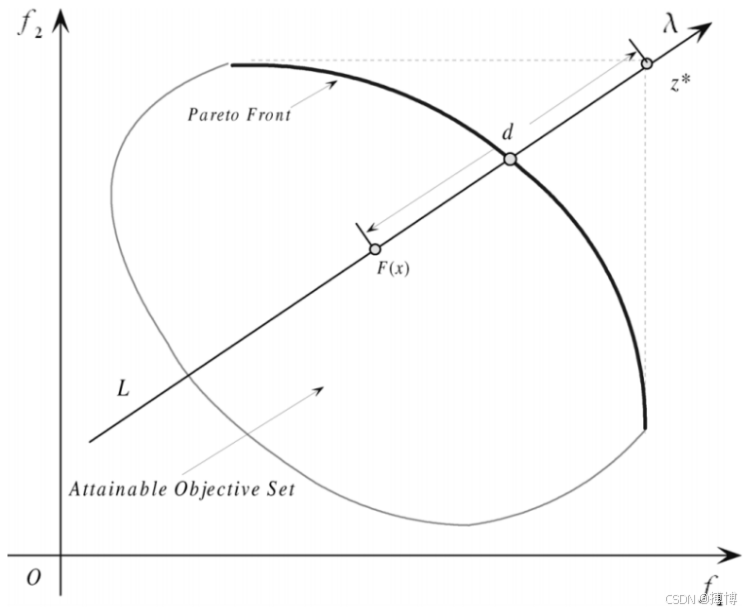
多目标优化算法之一:基于分解的方法
在多目标优化算法中,“基于分解的方法”通常指的是将多目标优化问题(MOP)分解为多个单目标优化子问题,并同时优化这些子问题。这种方法的核心思想是通过引入权重向量或参考点,将多目标问题转化为多个标量优化问题,每个子问题都关注于原始问题的一个特定方面或视角。这样可…...

conntrack iptables 安全组
centos 安装yum install conntrack-tools 1. conntrack状态 NEW: 新建连接(第一次包)。 ESTABLISHED: 已建立连接,正在传输数据。 RELATED: 与已有连接相关的连接,如 FTP 数据连接。 INVALID: 无效连接,无法识别或不…...

stringRedisTemplate.execute执行lua脚本
stringRedisTemplate.execute执行lua脚本 1. 引入必要依赖 确保项目中已经引入了Spring Data Redis相关依赖,例如在 Maven 项目中,一般会有如下依赖(版本号根据实际情况调整): <dependency><groupId>or…...
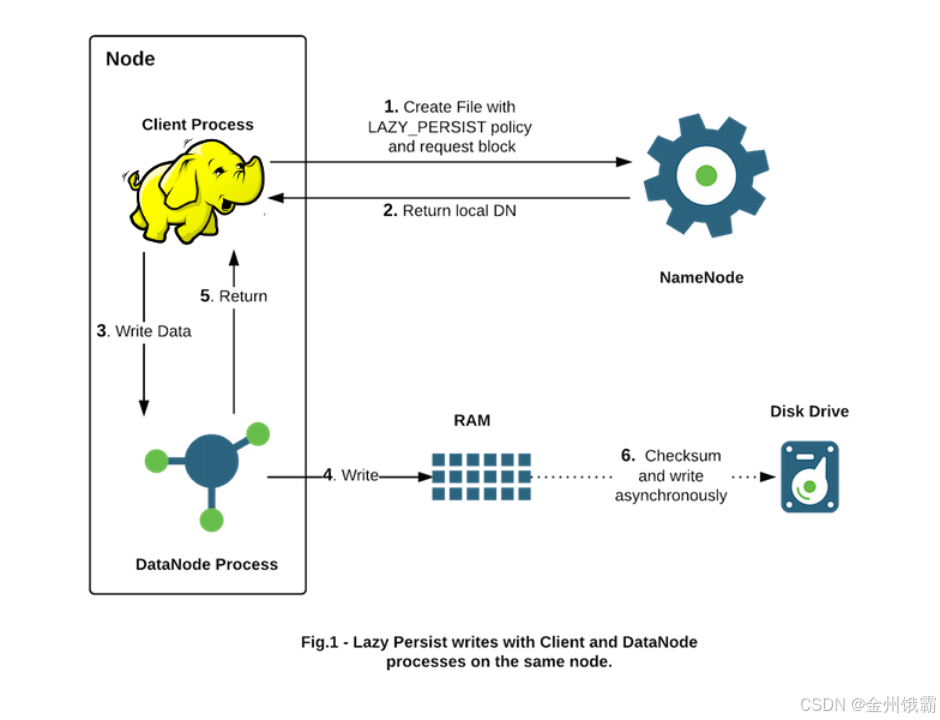
HDFS异构存储和存储策略
一、HDFS异构存储类型 1.1 冷、热、温、冻数据 通常,公司或者组织总是有相当多的历史数据占用昂贵的存储空间。典型的数据使用模式是新传入的数据被应用程序大量使用,从而该数据被标记为"热"数据。随着时间的推移,存储的数据每周…...

生成idea ui风格界面代码
创建一个类似 IntelliJ IDEA 的用户界面(UI)涉及多个组件和复杂的布局设计。为了简化这个过程,我们可以使用 **Java Swing** 或 **JavaFX** 来实现一个基本的 IDE 界面,模仿 IntelliJ IDEA 的主要布局元素,如菜单栏、工…...

嵌入式C语言:二维数组
目录 一、二维数组的定义 二、内存布局 2.1. 内存布局特点 2.2. 内存布局示例 2.2.1. 数组元素地址 2.2.2. 内存布局图(简化表示) 2.3. 初始化对内存布局的影响 三、访问二维数组元素 3.1. 常规下标访问方式 3.2. 通过指针访问 3.2.1. 指向数…...

【机器学习:四、多输入变量的回归问题】
多输入变量的回归问题 1. 多元线性回归概述 1.1 单变量线性回归与多变量线性回归的概念区分 单变量线性回归:用于预测一个因变量(输出变量)与单一自变量(输入变量)之间的线性关系。模型形式为: y θ 0 …...
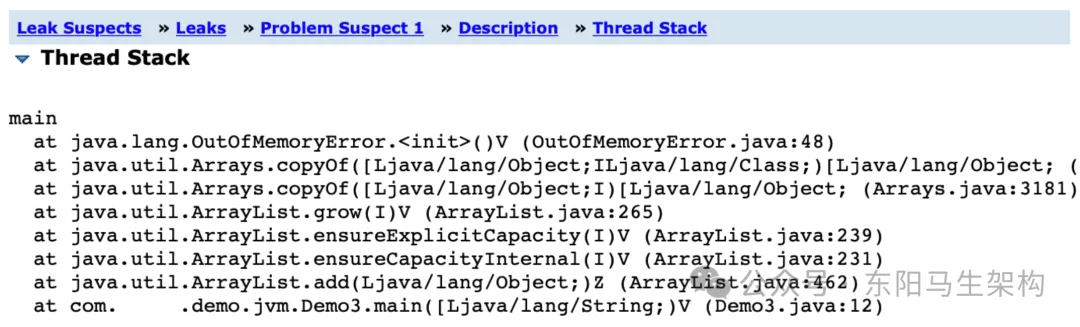
JVM实战—OOM的定位和解决
1.如何对系统的OOM异常进行监控和报警 (1)最佳的解决方案 最佳的OOM监控方案就是:建立一套监控平台,比如搭建Zabbix、Open-Falcon之类的监控平台。如果有监控平台,就可以接入系统异常的监控和报警,可以设置当系统出现OOM异常&…...
iOS 本地新项目上传git仓库,并使用sourceTree管理
此文记录的场景描述: iOS前期开发时,在本地创建项目,直至开发一段时间,初期编码及框架已完善后,才拿到git仓库的地址。此时需要将本地代码上传到git仓库。 上传至git仓库,可以使用终端,键入命令…...

mysql之基本select语句 运算符 排序分页
1.SQL的分类 DDL:数据定义语言. CREATE ALTER DROP RENAME TRUNCATE DML: 数据操作语言. INSERT DELETE UPDATE SELECT 重中之重 DCL: 数据控制语言. COMMIT ROLLBACK SAVEPOINT GRANT REVOKE 2.SQL语言的规则与规范 1.基本规则 SQL可以在一行或多行,为了提高可…...

如何在 Ubuntu 22.04 上安装 Nagios 服务器教程
简介 在本教程中,我们将解释如何在 Ubuntu 22.04 上安装和配置 Nagios,使用 Apache 作为 Web 服务器,并通过 Let’s Encrypt Certbot 使用 SSL 证书进行保护。 Nagios 是一个强大的监控系统,它可以帮助组织在 IT 基础设施问题影…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...


