【大数据】机器学习------支持向量机(SVM)
支持向量机的基本概念和数学公式:
1. 线性可分的支持向量机
对于线性可分的数据集
,其中(x_i \in R^d) 是特征向量
是类别标签,目标是找到一个超平面

,使得对于所有
的样本

,对于所有(y_i = -1) 的样本,(w^T x_i + b \leq -1)。
间隔(M)定义为:
目标是最大化间隔,即最小化(\frac{1}{2}|w|^2),同时满足

2. 对偶问题
通过引入拉格朗日乘子(\alpha_i\geq 0),原问题的拉格朗日函数为:

对偶问题通过对(L)求(w)和(b)的偏导数并令其为(0)得到:


对偶问题是最大化

约束条件为
3. 核函数
核函数
,将数据映射到高维空间。常见的核函数有:
-
线性核:
-

-
多项式核:

-
径向基函数(RBF)核:

4. 软间隔与正则化
引入松弛变量(\xi_i\geq 0),目标函数变为:

约束条件为


5. 支持向量回归(SVR)
对于回归问题,引入(\epsilon)-不敏感损失函数,目标是找到(w) 和(b) 使得:

约束条件为


代码示例(使用 Python 和 scikit-learn 库):
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC, SVR
from sklearn.metrics import accuracy_score, mean_squared_error
import numpy as np# 生成示例数据集
X, y = datasets.make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)
y[y == 0] = -1 # 将类别标签转换为 -1 和 1# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 线性 SVM 分类器
svm_classifier = SVC(kernel='linear', C=1.0)
svm_classifier.fit(X_train, y_train)
y_pred = svm_classifier.predict(X_test)
print("线性 SVM 分类准确率:", accuracy_score(y_test, y_pred))# 多项式核 SVM 分类器
svm_poly_classifier = SVC(kernel='poly', degree=3, C=1.0)
svm_poly_classifier.fit(X_train, y_train)
y_pred_poly = svm_poly_classifier.predict(X_test)
print("多项式核 SVM 分类准确率:", accuracy_score(y_test, y_pred_poly))# RBF 核 SVM 分类器
svm_rbf_classifier = SVC(kernel='rbf', gamma=0.7, C=1.0)
svm_rbf_classifier.fit(X_train, y_train)
y_pred_rbf = svm_rbf_classifier.predict(X_test)
print("RBF 核 SVM 分类准确率:", accuracy_score(y_test, y_pred_rbf))# 生成回归数据集
X_reg, y_reg = datasets.make_regression(n_samples=100, n_features=1, noise=0.1, random_state=42)
X_train_reg, X_test_reg, y_train_reg, y_test_reg = train_test_split(X_reg, y_reg, test_size=0.3, random_state=42)# 支持向量回归
svr = SVR(kernel='rbf', C=1.0, epsilon=0.2)
svr.fit(X_train_reg, y_train_reg)
y_pred_reg = svr.predict(X_test_reg)
print("SVR 均方误差:", mean_squared_error(y_test_reg, y_pred_reg))

代码解释:
datasets.make_classification:生成分类数据集。
train_test_split:将数据集划分为训练集和测试集。SVC:支持向量分类器,可指定不同的核函数(linear、poly、rbf等)和正则化参数C。accuracy_score:计算分类准确率。datasets.make_regression:生成回归数据集。SVR:支持向量回归,可指定核函数、正则化参数C和(\epsilon) 参数。mean_squared_error:计算均方误差。
手动实现 SVM 分类器(简化版):
import numpy as npdef linear_kernel(x1, x2):return np.dot(x1, x2)def train_svm(X, y, C=1.0, max_iter=1000, tol=1e-3, kernel=linear_kernel):n_samples, n_features = X.shapealpha = np.zeros(n_samples)b = 0eta = 0L = 0H = 0for iteration in range(max_iter):num_changed_alphas = 0for i in range(n_samples):Ei = np.sum(alpha * y * kernel(X, X[i])) + b - y[i]if (y[i] * Ei < -tol and alpha[i] < C) or (y[i] * Ei > tol and alpha[i] > 0):j = np.random.choice([k for k in range(n_samples) if k!= i])Ej = np.sum(alpha * y * kernel(X, X[j])) + b - y[j]alpha_i_old = alpha[i]alpha_j_old = alpha[j]if y[i] == y[j]:L = max(0, alpha[j] + alpha[i] - C)H = min(C, alpha[j] + alpha[i])else:L = max(0, alpha[j] - alpha[i])H = min(C, C + alpha[j] - alpha[i])if L == H:continueeta = 2 * kernel(X[i], X[j]) - kernel(X[i], X[i]) - kernel(X[j], X[j])if eta >= 0:continuealpha[j] -= y[j] * (Ei - Ej) / etaalpha[j] = np.clip(alpha[j], L, H)if abs(alpha[j] - alpha_j_old) < tol:continuealpha[i] += y[i] * y[j] * (alpha_j_old - alpha[j])b1 = b - Ei - y[i] * (alpha[i] - alpha_i_old) * kernel(X[i], X[i]) - y[j] * (alpha[j] - alpha_j_old) * kernel(X[i], X[j])b2 = b - Ej - y[i] * (alpha[i] - alpha_i_old) * kernel(X[i], X[j]) - y[j] * (alpha[j] - alpha_j_old) * kernel(X[j], X[j])if 0 < alpha[i] < C:b = b1elif 0 < alpha[j] < C:b = b2else:b = (b1 + b2) / 2num_changed_alphas += 1if num_changed_alphas == 0:breakreturn alpha, bdef predict_svm(X, alpha, b, X_train, y_train, kernel=linear_kernel):n_samples = X.shape[0]y_pred = []for i in range(n_samples):pred = np.sum(alpha * y_train * kernel(X_train, X[i])) + by_pred.append(np.sign(pred))return np.array(y_pred)# 示例使用
X = np.array([[1, 2], [2, 3], [3, 4], [6, 7], [7, 8], [8, 9]])
y = np.array([1, 1, 1, -1, -1, -1])
alpha, b = train_svm(X, y, C=1.0)
y_pred = predict_svm(X, alpha, b, X, y)
print("手动实现 SVM 预测结果:", y_pred)

代码解释:
linear_kernel:定义线性核函数。
train_svm:使用 SMO(Sequential Minimal Optimization)算法训练 SVM,更新拉格朗日乘子(\alpha) 和偏置(b)。predict_svm:使用训练好的(\alpha) 和(b) 进行预测。

相关文章:

【大数据】机器学习------支持向量机(SVM)
支持向量机的基本概念和数学公式: 1. 线性可分的支持向量机 对于线性可分的数据集 ,其中(x_i \in R^d) 是特征向量 是类别标签,目标是找到一个超平面 ,使得对于所有 的样本 ,对于所有(y_i -1) 的样本,…...

Android系统开发(八):从麦克风到扬声器,音频HAL框架的奇妙之旅
引言:音浪太强,我稳如老 HAL! 如果有一天你的耳机里传来的不是《咱们屯里人》,而是金属碰撞般的杂音,那你可能已经感受到了 Android 音频硬件抽象层 (HAL) 出问题的后果!在 Android 音频架构中,…...

Golang Gin系列-2:搭建Gin 框架环境
开始网络开发之旅通常是从选择合适的工具开始的。在这个全面的指南中,我们将引导你完成安装Go编程语言和Gin框架的过程,Gin框架是Go的轻量级和灵活的web框架。从设置Go工作空间到将Gin整合到项目中,本指南是高效而强大的web开发路线图。 安装…...

FGC_grasp复现
复现FGC_grasp 环境配置数据集准备RuntimeError: CUDA error: invalid device ordinal 问题的解决方案raise BadZipFile("File is not a zip file") zipfile.BadZipFile: File is not a zip file问题的解决方案加载数据集时总是被kill然后服务器也卡住了动不了问题的…...
实力认证 | 海云安入选《信创安全产品及服务购买决策参考》
近日,国内知名安全调研机构GoUpSec发布了2024年中国网络安全行业《信创安全产品及服务购买决策参考》,报告从产品特点、产品优势、成功案例、安全策略等维度对各厂商信创安全产品及服务进行调研了解。 海云安凭借AI大模型技术在信创安全领域中的创新应用…...
Avalonia系列文章之小试牛刀
最近有朋友反馈,能否分享一下Avalonia相关的文章,于是就抽空学习了一下,发现Avalonia真的是一款非常不错的UI框架,值得花时间认真学习一下,于是边学习边记录,整理成文,分享给大家,希…...

中国数字安全产业年度报告(2024)
数字安全是指,在全球数字化背景下,合理控制个人、组织、国家在各种活动中面临的数字风险,保障数字社会可持续发展的政策法规、管理措施、技术方法等安全手段的总和。 数字安全领域可从三个方面对应新质生产力的三大内涵:一是基于大型语言模型…...
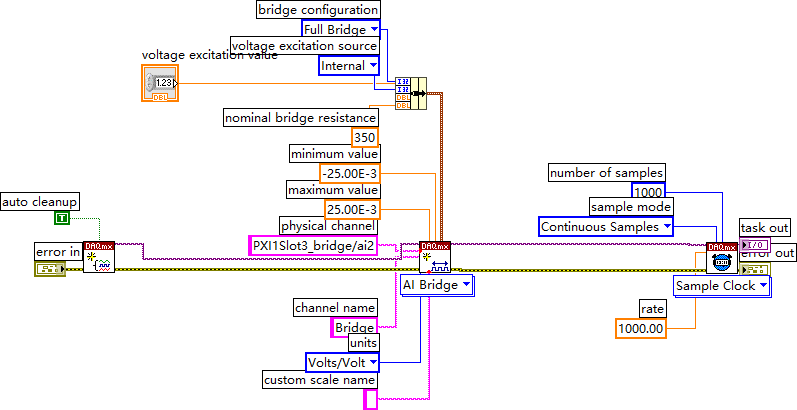
LabVIEW桥接传感器配置与数据采集
该LabVIEW程序主要用于配置桥接传感器并进行数据采集,涉及电压激励、桥接电阻、采样设置及错误处理。第一个VI("Auto Cleanup")用于自动清理资源,建议保留以确保系统稳定运行。 以下是对图像中各个组件的详细解释&#…...

简明docker快速入门并实践方法
简明docker快速入门并实践方法 前言:1. 什么是Docker?2. Docker的基本概念3. 安装配置Docker4. Docker基本命令:5. 简单实践:拉取Nginx镜像-自定义配置-推送镜像步骤 1:拉取Nginx镜像步骤 1.5(可选…...
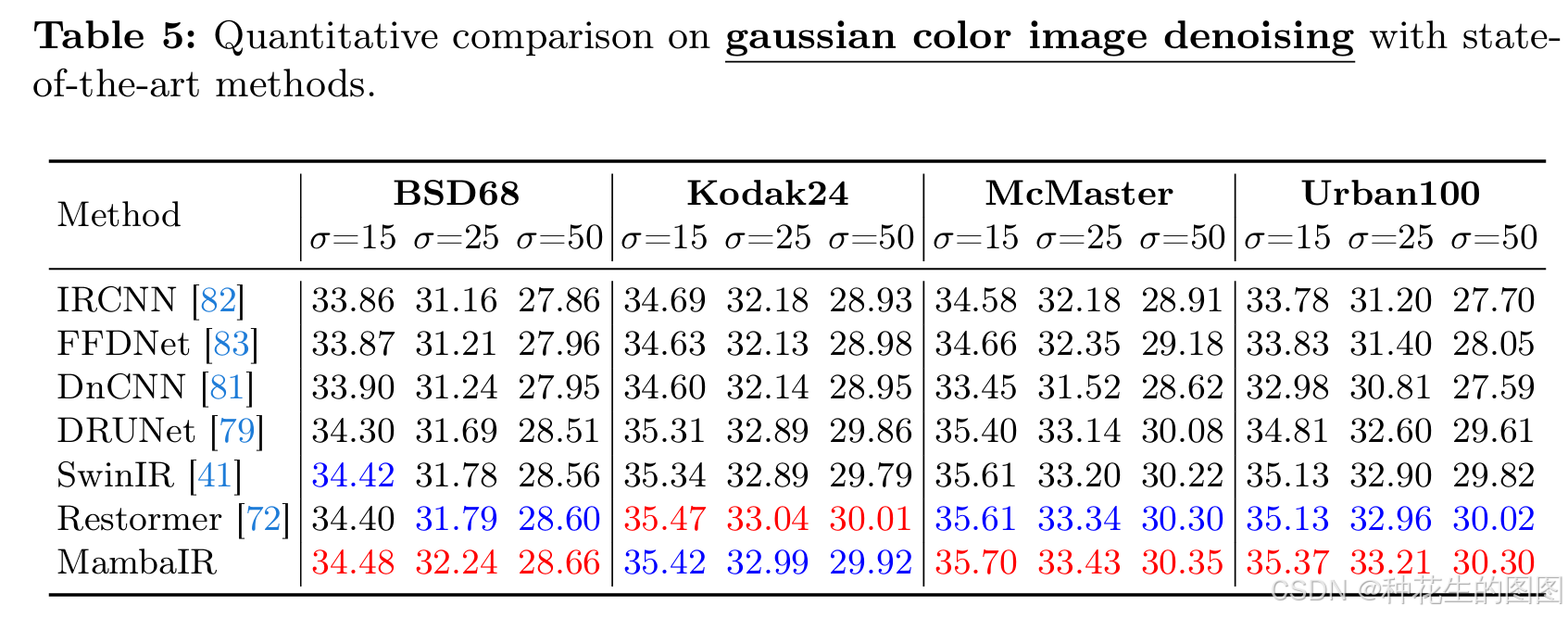
《MambaIR:一种基于状态空间模型的简单图像修复基线方法》学习笔记
paper:2402.15648 目录 摘要 一、引言 1、模型性能的提升依赖于网络感受野的扩大: 2、全局感受野和高效计算之间存在固有矛盾: 3、改进版 Mamba的巨大潜力 4、Mamba 在图像修复任务中仍面临以下挑战: 5、方法 6、主要贡献…...

链式前向星的写法
【图论02】动画说图的三种保存方式 降低理解门槛 邻接表 链式前向星 邻接矩阵_哔哩哔哩_bilibili 杭电ACM刘老师-算法入门培训-第12讲-拓扑排序及链式前向星_哔哩哔哩_bilibili 图论003链式前向星_哔哩哔哩_bilibili(链式前向星的遍历) head数组的下标…...

【逆境中绽放:万字回顾2024我在挑战中突破自我】
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” 文章目录 一、引言二、个人成长与盘点情感与心理成长学习与技能提升其它荣誉 三、年度创作历程回顾创作内容概…...
)
尺取法(算法优化技巧)
问题和序列的区间有关,且需要操作两个变量,可以用两个下标(指针)i 和 j 扫描区间。 1,反向扫描,i 从头,j 从尾,在中间相遇。 例1.1(P37) 找指定和的整数对…...

基于 K-Means 聚类分析实现人脸照片的快速分类
注:本文在创作过程中得到了 ChatGPT、DeepSeek、Kimi 的智能辅助支持,由作者本人完成最终审阅。 在 “视频是不能 P 的” 系列文章中,博主曾先后分享过人脸检测、人脸识别等相关主题的内容。今天,博主想和大家讨论的是人脸分类问题。你是否曾在人群中认错人,或是盯着熟人的…...
【漏洞预警】FortiOS 和 FortiProxy 身份认证绕过漏洞(CVE-2024-55591)
文章目录 一、产品简介二、漏洞描述三、影响版本四、漏洞检测方法五、解决方案 一、产品简介 FortiOS是Fortinet公司核心的网络安全操作系统,广泛应用于FortiGate下一代防火墙,为用户提供防火墙、VPN、入侵防御、应用控制等多种安全功能。 FortiProxy则…...
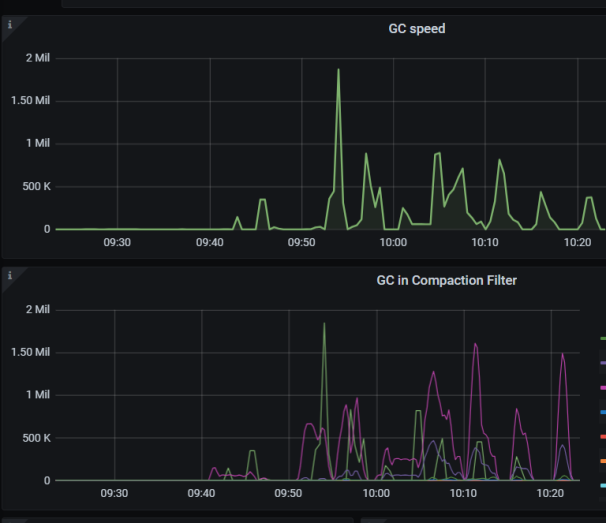
7.5.4 MVCC优化测试
作者: h5n1 原文来源: https://tidb.net/blog/4e02d900 1. 背景 由于MVCC 版本数量过多导致rocksdb扫描key数量过多影响SQL执行时间是tidb经常出现问的问题,tidb也一直在致力于优化该问题。 一些优化方式包括比: (1) 从传统…...

STM32 FreeRTOS 事件标志组
目录 事件标志组简介 基本概念 1、事件位(事件标志) 2、事件组 事件组和事件位数据类型 事件标志组和信号量的区别 事件标志组相关API函数介绍 事件标志组简介 基本概念 当在嵌入式系统中运行多个任务时,这些任务可能需要相互通信&am…...

生成树机制实验
1 实验内容 1、基于已有代码,实现生成树运行机制,对于给定拓扑(four_node_ring.py),计算输出相应状态下的生成树拓扑 2、构造一个不少于7个节点,冗余链路不少于2条的拓扑,节点和端口的命名规则可参考four_node_ring.py,使用stp程序计算输出生成树拓扑 2 实验原理 一、…...

企业分类相似度筛选实战:基于规则与向量方法的对比分析
文章目录 企业表相似类别筛选实战项目背景介绍效果展示基于规则的效果基于向量相似的效果 说明相关文章推荐 企业表相似类别筛选实战 项目背景 在当下RAG(检索增强生成)技术应用不断发展的背景下,掌握文本相似算法不仅能够助力信息检索&…...
2024年博客之星年度评选—创作影响力评审入围名单公布
2024年博客之星活动地址https://www.csdn.net/blogstar2024 TOP 300 榜单排名 用户昵称博客主页 身份 认证 评分 原创 博文 评分 平均 质量分评分 互动数据评分 总分排名三掌柜666三掌柜666-CSDN博客1001002001005001wkd_007wkd_007-CSDN博客1001002001005002栗筝ihttps:/…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
