计算机组成原理（2）王道学习笔记

数据的表示和运算

提问：1.数据如何在计算机中表示？

            2.运算器如何实现数据的算术、逻辑运算？

十进制计数法 

古印度人发明了阿拉伯数字：0，1，2，3，4，5，6，7，8，9（符号反映权重）

十进制：975=9x100+7x10+5x1 （符号所在的位置也反映权重）

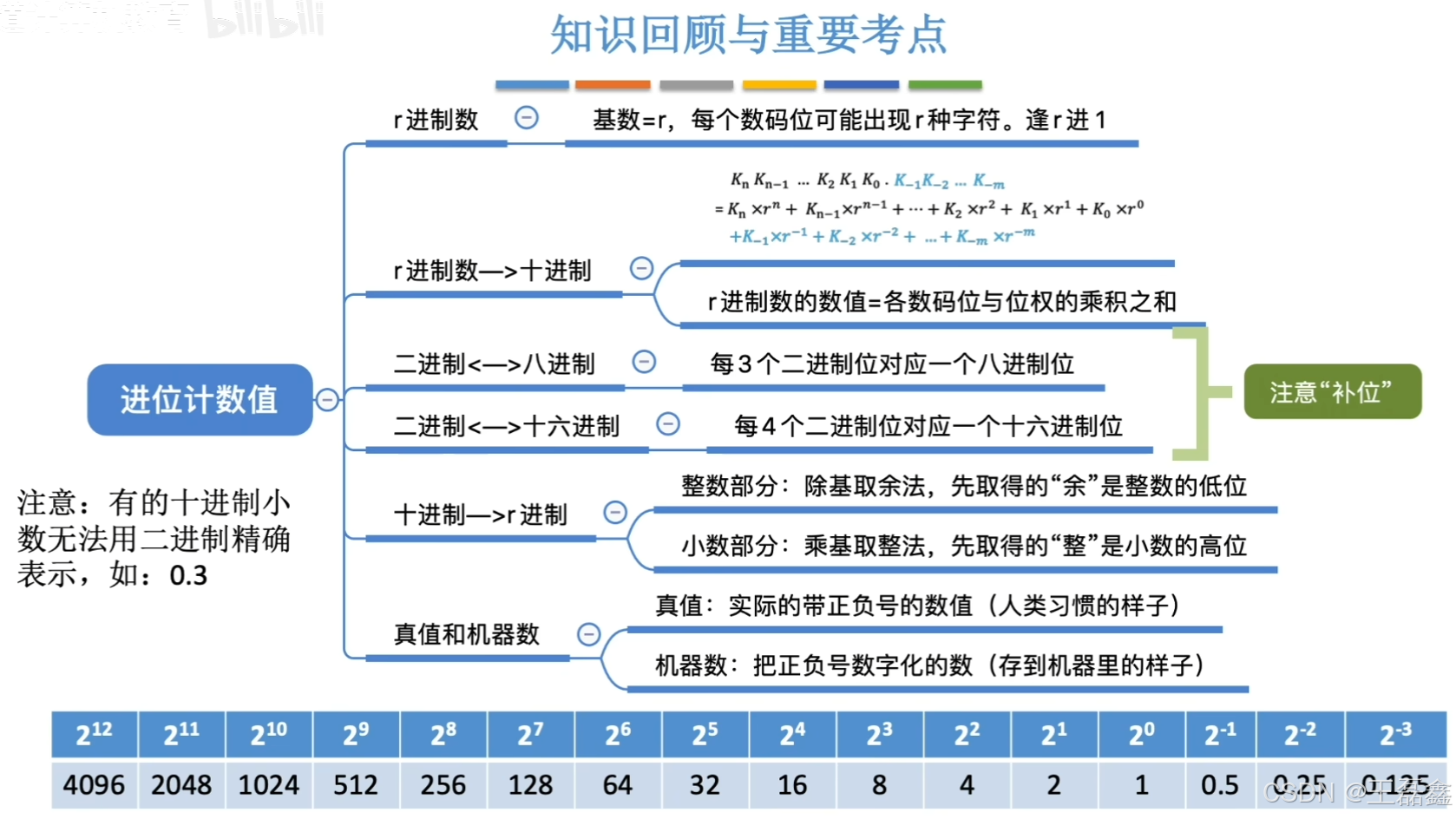
进位计数制：有0~9，共十种符号。逢十进一 

以此类推，十进制的这种计数方式，我们会用每一个数码位乘以这个数码位所对应的一个实际的权值。这些权值都是十的某次方，因此我们才把它叫做十进制。

 其实呢，十进制能推广到 r 进制。r 进制里，基数就是 r，每个数码位能用 r 种符号。像古巴比伦人用的 60 进制，每个数码位就有 60 种符号，现在咱们算时间，1 小时 60 分钟，就是 60 进制的应用呢。不过在计算机世界里，常用的是二进制、八进制和十六进制。

r进制计数法

1. 二进制：计算机中最常用基数为2的计数制即二进制。它仅有0和1两种数码，计数规则是“逢二进一”，任意数位的权为，i是所在位数。

2. 八进制：基数是8，有0 - 7共8个不同数码，计数“逢八进一”。由于r = 8=，所以把二进制中的3位数码编为一组就是1位八进制数码，二者转换很方便。

3. 十六进制：基数为16，有0 - 9、A - F共16个不同数码，其中A - F分别表示10 - 15，计数“逢十六进一”。因为r = 16 = ，所以4位二进制数码与1位十六进制数码相对应。可以用后缀字母标识数的进制，用B表示二进制数，用D表示十进制数（通常直接省略），用H表示十六进制数，有时也用前缀0x表示十六进制数。  

 在计算机中，有二进制、八进制、十进制、十六进制

计算机喜欢二进制，一是因为能用两个稳定状态的物理器件表示 0 和 1，像高电平低电平、电容电荷正负。二是 0 和 1 对应逻辑的假和真，方便做逻辑算。三是能用逻辑门电路做算术运算。不过二进制给人看不太方便，所以也常用八进制和十六进制。

二进制数转换为八进制数和十六进制数

对于一个二进制小数（既包含整数部分，又包含小数部分），在转换时应以小数点为界。其整数部分，从小数点开始往左数，将一串二进制数分为3位（八进制）一组或4位（十六进制）一组，在数的最左边可根据需要加“0”补齐；对于小数部分，从小数点开始往右数，也将一串二进制数分为3位一组或4位一组，在数的最右边也可根据需要加“0”补齐。最终使总的位数为3或4的整数倍，然后分别用对应的八进制数或十六进制数取代。  

 如果我们想要将二进制转换为八进制，那么只需要三个二进制为一组，然后将每组转换为对应的八进制符号即可。

各进制的常见书写方式

进制	书写方式 1	书写方式 2	书写方式 3
二进制		1010001010010B	-
八进制		-	-
十六进制		1652H	0x1652
十进制		1652D	-

十进制转换成任意进制数 

一个十进制数转换为任意进制数，通常采用基数乘除法（注意，基数的值与进制相关）。这种转换方法对十进制数的整数部分和小数部分将分别进行处理，对整数部分采用除基取余法，对小数部分采用乘基取整法，最后将整数部分与小数部分的转换结果拼接起来。

除基取余法（用于整数部分）：对整数部分进行除基取余操作，最先获取的余数是数的最低位，最后获取的余数是数的最高位（即“除基取余，先余为低，后余为高” ），当商为0时操作结束。  

乘积取整法（小数部分）：小数部分乘基取整，最先取得的整数为数的最高位，最后取得的整数为数的最低位（乘基取整，先整为高，后整为低），乘积为1.0（或满足精度要求）时结束。

 注意：

1. 十进制数转换为任意进制数时，对于除基取余法和乘基取整法，以及所取之数放置位置的原理，应结合 r 进制数的数值表示公式思考，避免死记硬背。
2. 在计算机中，整数和小数有区别，整数可连续表示，小数是离散的，不是每个十进制小数都能用二进制小数精确表示（如 0.3 乘二取整无法得到精确结果），但任意二进制小数都可用十进制小数精确表示，需引起重视。

 真值和机器数

真值：符合人类习惯的数字

机器数：数字实际存到机器里的形式，正负号需要被“数字化”。

类型	定义	正数示例（以 + 15 为例）	负数示例（以 - 8 为例）
原码	最高位为符号位，0 表示正数，1 表示负数，其余位为数值位的二进制表示	01111（假设用 5 位二进制表示，下同）	11000
反码	正数的反码与原码相同；负数的反码是在原码的基础上，符号位不变，其余各位取反	01111	10111
补码	正数的补码与原码相同；负数的补码是在反码的基础上 + 1	01111	11000
移码	在补码的基础上，将符号位取反（一般用于浮点数的阶码表示）	11111	01000