【深度之眼cs231n第七期】笔记(三十一)
目录
- 强化学习
- 什么是强化学习?
- 马尔可夫决策过程(MDP)
- Q-learning
- 策略梯度
- SOTA深度强化学习
还剩一点小尾巴,还是把它写完吧。(距离我写下前面那行字又过了好几个月了【咸鱼本鱼】)(汗颜,好久之前写了一半就忘了,后面的就直接看图吧)
cs231n的强化学习公式较多,我是看了李宏毅的强化学习才理解的。
强化学习
什么是强化学习?
总览:强化学习里有三个重要的概念:环境、agent和奖励。
它们的关系如下:
- 环境给予agent一个状态St;
- 在该状态下,agent采取行动At;
- 对于行动At,环境给出的奖励是Rt;
- 并且环境给予agent下一状态St+1,循环往复。
强化学习的目标是:学习如何行动能使奖励达到最大,我们能控制的只有行动,奖励和状态都是环境给予的。

举个具体的例子:
Atari游戏的状态是当前游戏界面;
agent可采取的行动有:上、下、左、右;
奖励:采取一步行动后,获得或减少的分数;
目标:以最高分完成游戏。

马尔可夫决策过程(MDP)
上面都是用文字描述的,现在用数学语言来描述一下强化学习S。
事实上,一个马尔可夫决策过程就是强化学习问题的数学表达。马尔可夫决策过程满足马尔可夫性。
马尔可夫性:当前状态完全刻画了世界状态,也就是说,下一状态完全依赖于当前状态。
马尔可夫决策过程由一组对象定义(S,A,R,P,γ)
- S是所有可能状态的集合
- A是所有可能行动的集合
- R是奖励的概率分布,由(状态,行动)给定
- P是跳到下一状态的概率,由(当前状态,行动)给定
- γ是奖励的衰退因子

用马尔可夫决策过程来描述强化学习:
- 在t=0时刻,环境采样初始状态S0
- 从t=0到学习结束:
- agent选择行动At
- 环境依概率给出奖励Rt(概率由R(.|St,At)决定)
- 环境依概率给出下一状态St+1(概率由P(.|St,At)决定)
- agent接收奖励Rt和状态St+1
我们所采取的行动组合a0,a1,a2……称为策略π
而强化学习的目标是找到一个策略π*,使得奖励之和最大。

最直接的解决办法是穷举所有的行动组合,计算每个组合的奖励,把奖励最大的选出来。但这其实有个问题,每次行动后,奖励和下一状态都是环境给予的,有一定的随机性。
也就是说即使每次执行的都是同一个行动组合π,最后的结果也可能相差很大,所以首先要解决奖励之和的随机性,这样我们才能比较哪个组合更好。而解决随机性最常用的方法是求期望。
所以现在问题变成了:找到一个π*,使得E(奖励之和)最大。

Q-learning
在解决如何找到最优策略π*之前,为了方便后面描述算法,先定义两个有用的函数:
值函数:在状态为s的情况下,遵从策略π后得到的E(奖励之和)
假设初始状态有3种:S0、S1和S2,那么策略π的E(奖励之和)=Vπ(S0)+Vπ(S1)+Vπ(S2)
Q值函数:在状态为s、行动为a的情况下,遵从策略π后得到的E(奖励之和)
假设状态为s时可采取的行动有3种:A0、A1和A2,那么Vπ(S0)=Qπ(S0,A0)+Qπ(S0,A1)+Qπ(S0,A2)

给定S0和A0的情况下,最优的策略π*能使Q值函数达到最大,记为Q*
而Q*满足bellman等式,这个等式想表达的东西很简单,就是当前最优的Q*=当前奖励r+下一状态下最优的Q*。
乍一看这个式子没有任何用,既然我不知道现在的Q*,当然也不会知道下一状态的Q*了。除非一直迭代到最后一个状态,但是前面提到了奖励和下一状态都是随机的,所以直接迭代会非常复杂,这条路行不通。
现在的问题是:Q*太复杂了,没办法直接表达,那能拿什么东西来替代吗?
这就轮到神经网络出场了,神经网络专门解决表达式过于复杂的问题。
假设使用神经网络QL来表示函数Q*,Q*有两个参数——状态s和行动a,那么QL也会有两个输入——s和a(如果行动是离散的,QL也可以设计为:输入s,输出n个标量,每个标量代表某一个行动下的E(奖励之和))。
QL会输出一个标量代表当前状态s和行动a的E(奖励之和),不同的输入会得到不同的E(奖励之和)
那么只要训练神经网络QL,使得QL(Si+1,Ai+1)-QL(Si,Ai)尽可能地接近Ri就可以了,这不就是一个简单的回归模型吗?
在训练好QL后,由于行动是有限的,所以可通过下面的方式找到π*:
- 在Si的状态下,使用遍历(行动是离散的)或梯度上升(行动是连续的)得到Ai,使得QL(S0,Ai)最大
- 环境根据Si和Ai给出Si+1
- 重复1、2步直到结束
- π*=A0A1A2……

上面提到的QL网络还有三个问题:
- QL的训练方式是使QL(Si+1,Ai+1)-QL(Si,Ai)尽量接近Ri,每次更新时QL(Si,Ai)和QL(Si+1,Ai+1)的值会同时改变,造成训练的不稳定。
所以在实际训练中会有两个神经网络,QL和QLtarget,QLtarget-QL尽量接近Ri。
每次反向传播时只更新QL,在经过N次迭代后再把QL的参数赋值给QLtarget

- 由于QL网络的训练方式是:与环境互动一次,更新QL,根据更新后的QL获得下一行动a,使用a和环境互动……
下一个行动a与当前行动高度相关,这会导致训练效果不好,就像进入一家新餐厅时,随机点了一道菜,味道还可以,从此以后就再也不尝试其他菜了。
解决办法是:准备一个缓冲区,每次互动后把数据存入缓冲区,再从缓冲区随机选取数据进行训练。
这种办法还有一个好处,可以多次使用训练数据。一般来说,在强化学习中,与环境互动才是最费时间的。

- 对于一个复杂的问题,比如让机器人抓住某个物体,Q函数很难通过随机尝试学到一个具体的行动来解决这个问题。那么可不可以换一个方向,不需要机器人学习具体的行动,而是学习一个“握住”的策略?

策略梯度
策略梯度网络PG的输入是状态s,输出是下一步采用某个行动的概率p(a|s)(而上面的QL网络的输出是采用某个动作后的E(奖励之和))。
在网络PG固定的情况下,可得到多个策略πθ,每个策略有一定的概率:

也可以计算出πθ的奖励之和

如果穷举所有的行为轨迹πθ,那么可以计算出E(奖励之和),记为J(θ)

J(θ)是由θ决定的,而且我们的目标是最大化J(θ),那么可以考虑对参数θ进行梯度上升(目标函数是J(θ))

课程里用了好几页PPT和大段大段的公式来讨论J(θ)能不能求导,要怎么进行梯度上升,由于我这里直接把函数看做神经网络GP了,就不展示相应的细节了(神经网络当然可以求导,进行梯度上升也很容易,神经网络牛逼!而且删掉公式之后,脉络越发清晰起来了。)
下面是一些训练技巧:
- 增加baseline
如果奖励永远都是正的,那么任何行动都会导致J(θ)增加,从而增加该行动的概率。
而所有概率之和为1,其他行动只是不幸没有被采样到就得降低概率,这是不符合要求的。
所以希望奖励有正有负,这可以通过减去一个baseline来达成,历史奖励平均值是一个常用的baseline。






SOTA深度强化学习












cs231n系列终于写完了,其实后面还有两课,一课是讲硬件加速和模型轻量化,另一课是讲“为什么稍微改变一张熊猫的照片就可以让计算机把它认为是长臂猿(人眼看不出任何差别)”,但对这两个方面不是很熟悉(轻量化还好,后一课真的一知半解的),就不乱写了。
不写的最主要的原因其实是:我进了GAN的深渊……
相关文章:

【深度之眼cs231n第七期】笔记(三十一)
目录 强化学习什么是强化学习?马尔可夫决策过程(MDP)Q-learning策略梯度SOTA深度强化学习 还剩一点小尾巴,还是把它写完吧。(距离我写下前面那行字又过了好几个月了【咸鱼本鱼】)(汗颜ÿ…...
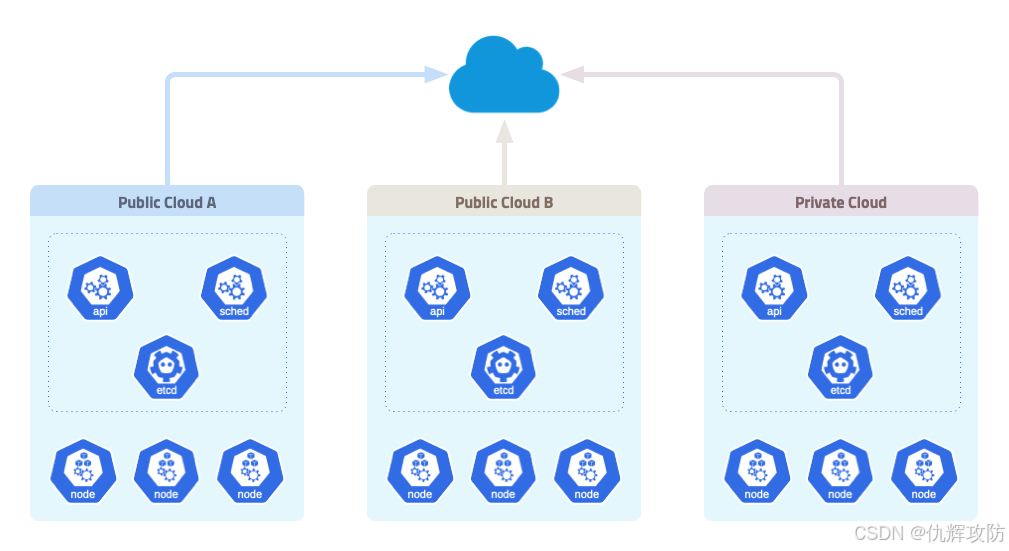
【云安全】云原生-K8S-简介
K8S简介 Kubernetes(简称K8S)是一种开源的容器编排平台,用于管理容器化应用的部署、扩展和运维。它由Google于2014年开源并交给CNCF(Cloud Native Computing Foundation)维护。K8S通过提供自动化、灵活的功能…...

SpringBoot中Excel表的导入、导出功能的实现
文章目录 一、easyExcel简介二、Excel表的导出2.1 添加 Maven 依赖2.2 创建导出数据的实体类4. 编写导出接口5. 前端代码6. 实现效果 三、excel表的导出1. Excel表导入的整体流程1.1 配置文件存储路径 2. 前端实现2.1 文件上传组件 2.2 文件上传逻辑3. 后端实现3.1 文件上传接口…...
)
Spark入门(Python)
目录 一、安装Spark 二、Spark基本操作 一、安装Spark pip3 install pyspark 二、Spark基本操作 # 导入spark的SparkContext,SparkConf模块 from pyspark import SparkContext, SparkConf # 导入os模块 import os # 设置PYSPARK的python环境 os.environ[PYSPARK_PYTHON] &…...

Daemon进程创建过程
Daemon创建过程: 1、fork,创建子进程。退出父进程。 2、setsid,创建新会话。脱离原会话、进程组、控制终端。 再次fork,与终端完全脱离。第二次fork的意义???? 先脱离原父进程&#…...

在sortablejs的拖拽排序情况下阻止input拖拽事件
如题 问题 在vue3的elementPlus的table中,通过sortablejs添加了行拖拽功能,但是在行内会有输入框,此时拖拽输入框会触发sortablejs的拖拽功能 解决 基于这个现象,我怀疑是由于拖拽事件未绑定而冒泡到后面的行上从而导致的拖拽…...

C++初阶—string类
第一章:为什么要学习string类 1.1 C语言中的字符串 C语言中,字符串是以\0结尾的一些字符的集合,为了操作方便,C标准库中提供了一些str系列的库函数,但是这些库函数与字符串是分离开的,不太符合OOP的思想&…...

C# 提取PDF表单数据
目录 使用工具 C# 提取多个PDF表单域的数据 C# 提取特定PDF表单域的数据 PDF表单是一种常见的数据收集工具,广泛应用于调查问卷、业务合同等场景。凭借出色的跨平台兼容性和标准化特点,PDF表单在各行各业中得到了广泛应用。然而,当需要整合…...

算法刷题Day28:BM66 最长公共子串
题目链接,点击跳转 题目描述: 解题思路: 方法一:暴力枚举 遍历str1的每个字符x,并在str2中寻找以相同元素x为起始的最长字符串。记录最长的公共子串及其长度。 代码实现: def LCS(self, str1: str, st…...
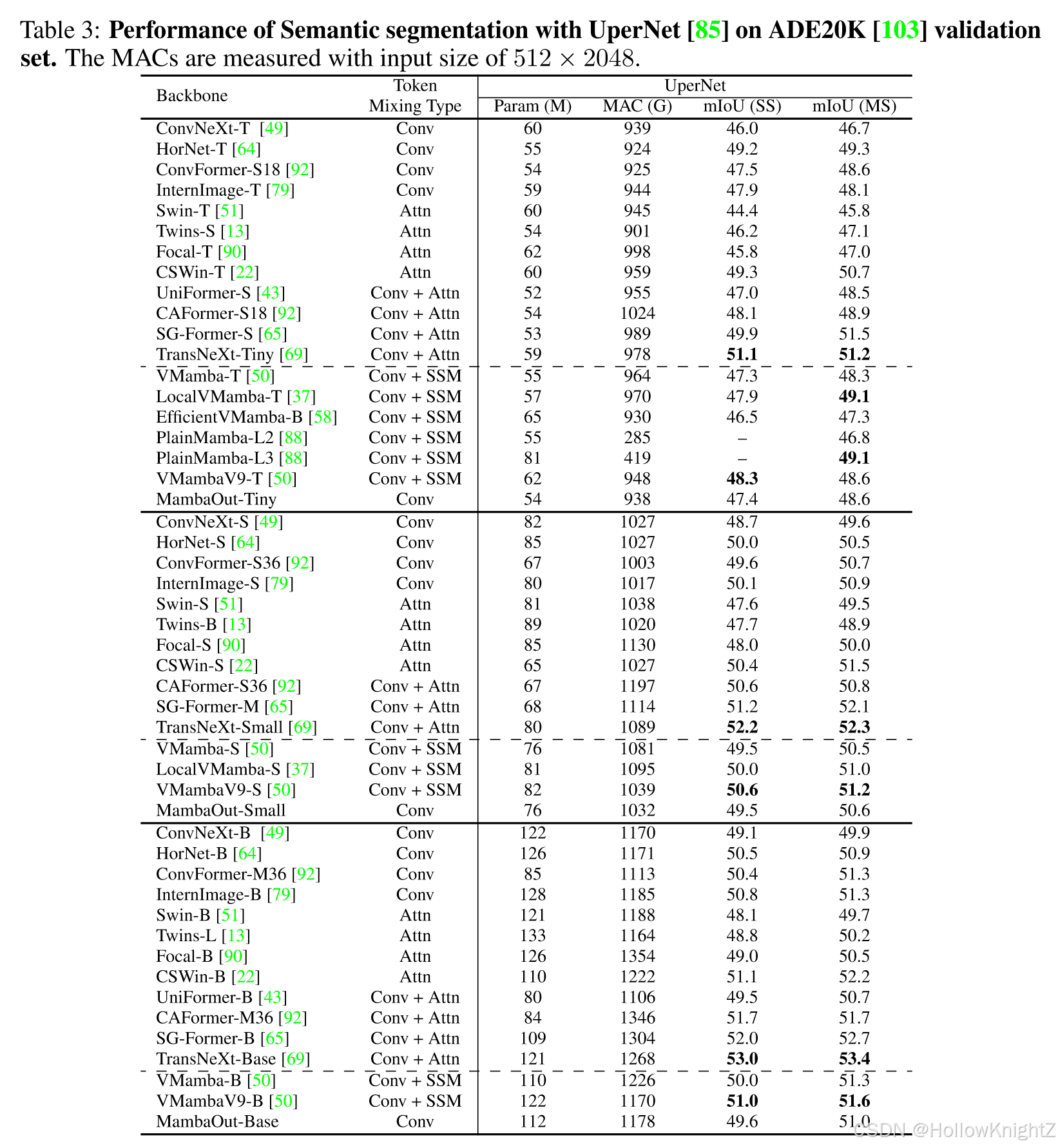
论文阅读笔记:MambaOut: Do We Really Need Mamba for Vision?
论文阅读笔记:MambaOut: Do We Really Need Mamba for Vision? 1 背景2 创新点3 方法4 模块4.1 Mamba适合什么任务4.2 视觉识别任务是否有很长的序列4.3 视觉任务是否需要因果token混合模式4.4 关于Mamba对于视觉的必要性假设 5 效果 论文:https://arxi…...
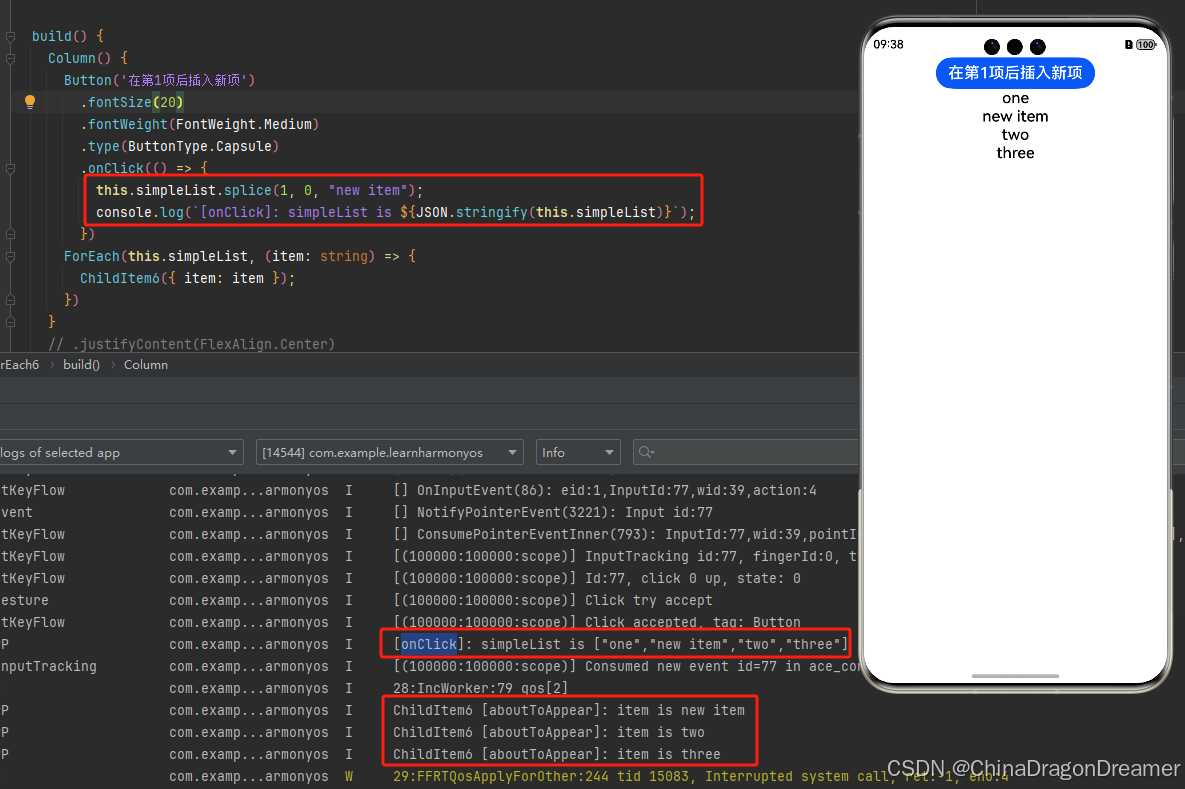
HarmonyOS:ForEach:循环渲染
一、前言 ForEach接口基于数组类型数据来进行循环渲染,需要与容器组件配合使用,且接口返回的组件应当是允许包含在ForEach父容器组件中的子组件。例如,ListItem组件要求ForEach的父容器组件必须为List组件。 API参数说明见:ForEa…...

Python3 【函数】项目实战:5 个新颖的学习案例
Python3 【函数】项目实战:5 个新颖的学习案例 本文包含5编程学习案例,具体项目如下: 简易聊天机器人待办事项提醒器密码生成器简易文本分析工具简易文件加密解密工具 项目 1:简易聊天机器人 功能描述: 实现一个简易…...

XSS 漏洞全面解析:原理、危害与防范
目录 前言编辑 漏洞原理 XSS 漏洞的危害 检测 XSS 漏洞的方法 防范 XSS 漏洞的措施 前言 在网络安全的复杂版图中,XSS 漏洞,即跨站脚本攻击(Cross - Site Scripting),是一类极为普遍且威胁巨大的安全隐患。随着互…...

从 GShard 到 DeepSeek-V3:回顾 MoE 大模型负载均衡策略演进
作者:小天狼星不来客 原文:https://zhuanlan.zhihu.com/p/19117825360 故事要从 GShard 说起——当时,人们意识到拥有数十亿甚至数万亿参数的模型可以通过某种形式的“稀疏化(sparsified)”来在保持高精度的同时加速训…...

【回溯+剪枝】回溯算法的概念 全排列问题
文章目录 46. 全排列Ⅰ. 什么是回溯算法❓❓❓Ⅱ. 回溯算法的应用1、组合问题2、排列问题3、子集问题 Ⅲ. 解题思路:回溯 剪枝 46. 全排列 46. 全排列 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 …...

Flutter解决macbook M芯片Android Studio中不显示IOS真机的问题
下载了最新的Android Studio LadyBug 下载了最新的xcode16.2 结果,只有安卓真机才在Android studio显示, IOS真机只在xcode显示 IOS真机不在android studio显示。 解决方法是: 在终端运行如下命令: sudo xcode-select -s /Applic…...

自签证书的dockerfile中from命令无法拉取镜像而docker的pull命令能拉取镜像
问题现象: docker pull images拉取镜像正常 dockerfile中的from命令拉取镜像就会报出证书错误。报错信息如下: [bjxtbwj-kvm-test-jenkins-6-243 ceshi_dockerfile]$ docker build . [] Building 0.4s (3/3) FINISHED …...

【MySQL】--- 复合查询 内外连接
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏: MySQL 🏠 基本查询回顾 假设有以下表结构: 查询工资高于500或岗位为MANAGER的雇员,同时还要满足他们的姓名首字母为…...

QT TLS initialization failed
qt使用QNetworkAccessManager下载文件(给出的链接可以在浏览器里面下载文件),下载失败, 提示“TLS initialization failed”通常是由于Qt在使用HTTPS进行文件下载时,未能正确初始化TLS(安全传输层协议&…...

系统学英语 — 句法 — 复合句
目录 文章目录 目录复合句型主语从句宾语从句表语从句定语从句状语从句同位语从句 复合句型 复合句型,即:从句。在英语中,除了谓语之外的所有句子成分都可以使用从句来充当。 主语从句 充当主语的句子,通常位于谓语之前&#x…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
