考试知识点位运算
深入理解位运算
在C++编程的世界里,位运算作为一种直接对二进制位进行操作的运算方式,虽然不像加减乘除等算术运算那样广为人知,却在许多关键领域发挥着至关重要的作用。从底层系统开发到高效算法设计,位运算都展现出其独特的魅力与强大的功能。同时,掌握一些位运算的小技巧,在考试涉及相关计算时能帮助我们快速得出答案。
一、位运算基础
(一)按位与(&)
按位与运算会对两个操作数对应的二进制位进行比较,只有当两个对应位都为1时,结果位才为1,否则为0。例如,5(二进制为00000101)与3(二进制为00000011)进行按位与运算:
#include <iostream>
int main() {int a = 5;int b = 3;int result = a & b;std::cout << "5 & 3 的结果是: " << result << std::endl;return 0;
}
在这个例子中,00000101与00000011按位与后得到00000001,即结果为1。按位与运算常用于掩码操作,比如提取一个整数特定的二进制位。
(二)按位或(|)
按位或运算与按位与相反,只要两个对应位中有一个为1,结果位就为1,只有当两个对应位都为0时,结果位才为0。还是以5和3为例:
#include <iostream>
int main() {int a = 5;int b = 3;int result = a | b;std::cout << "5 | 3 的结果是: " << result << std::endl;return 0;
}
00000101与00000011按位或后得到00000111,即结果为7。按位或运算常被用于设置某些二进制位为1。
(三)按位异或(^)
按位异或运算当两个对应位不同时,结果位为1,相同时结果位为0。同样对5和3进行操作:
#include <iostream>
int main() {int a = 5;int b = 3;int result = a ^ b;std::cout << "5 ^ 3 的结果是: " << result << std::endl;return 0;
}
00000101与00000011按位异或后得到00000110,即结果为6。按位异或有一个有趣的特性,就是对同一个数进行两次异或操作会得到原数,这在数据加密等领域有应用。
(四)按位取反(~)
按位取反是一元运算符,它将操作数的每一位都取反,0变为1,1变为0。例如对5进行按位取反:
#include <iostream>
int main() {int a = 5;int result = ~a;std::cout << "~5 的结果是: " << result << std::endl;return 0;
}
5的二进制00000101取反后得到11111010,在有符号整数表示中,这是一个负数(-6)。
(五)左移(<<)和右移(>>)
左移运算符(<<)将操作数的二进制位向左移动指定的位数,右边空出的位补0。例如,3(二进制00000011)左移2位:
#include <iostream>
int main() {int a = 3;int result = a << 2;std::cout << "3 << 2 的结果是: " << result << std::endl;return 0;
}
00000011左移2位后变为00001100,即结果为12。左移操作相当于对整数乘以2的移动位数次方。
右移运算符(>>)则将操作数的二进制位向右移动指定的位数。对于无符号整数,左边空出的位补0;对于有符号整数,若为正数左边补0,若为负数左边补1(算术右移)。例如,12(二进制00001100)右移2位:
#include <iostream>
int main() {int a = 12;int result = a >> 2;std::cout << "12 >> 2 的结果是: " << result << std::endl;return 0;
}
00001100右移2位后变为00000011,即结果为3。右移操作相当于对整数除以2的移动位数次方(向下取整)。
二、考试计算小技巧
(一)巧用左移快速乘2的幂
在考试中,如果遇到需要计算一个整数乘以2的幂次方的情况,使用左移运算符会非常高效。例如,计算5乘以8(即2的3次方),常规乘法计算可能需要花费一定时间,但用位运算就简单很多。因为5的二进制是00000101,左移3位后变成00101000,对应的十进制数就是40。所以在草稿纸上简单写下二进制数并进行左移操作,就能快速得出答案,比传统乘法计算更节省时间。
(二)右移实现快速整除2的幂
与左移对应,右移可以快速实现整除2的幂次方的计算。比如计算24除以4(即2的2次方),24的二进制是00011000,右移2位后变为00000110,也就是十进制的6。这种方法在处理除法运算且除数是2的幂时,能避免复杂的除法竖式计算,提高答题速度。
(三)按位与判断奇偶性
判断一个整数是奇数还是偶数,用按位与运算只需一步。因为奇数的二进制最低位是1,偶数的二进制最低位是0。所以将一个整数与1进行按位与运算,如果结果为1,则该数是奇数;如果结果为0,则该数是偶数。例如判断7的奇偶性,7的二进制是00000111,7 & 1的结果为1,所以7是奇数。这种技巧在涉及奇偶性判断的题目中,能快速给出答案,无需进行常规的取余运算。
(四)按位异或交换两个整数的值(无中间变量)
在一些编程概念或算法相关的考试题目中,可能会要求不使用中间变量交换两个整数的值。这时按位异或运算就派上用场了。假设有两个整数a和b,通过以下三步操作就能实现交换:
a = a ^ b;
b = a ^ b;
a = a ^ b;
例如a = 5(二进制00000101),b = 3(二进制00000011),第一步a = 5 ^ 3 = 6(二进制00000110);第二步b = 6 ^ 3 = 5(二进制00000101);第三步a = 6 ^ 5 = 3(二进制00000011),完成了a和b值的交换。在考试时遇到此类问题,使用这种方法能快速写出代码或给出解决方案。
三、位运算的实际应用
(一)状态标志管理
在程序中,经常需要表示多种状态。使用位运算可以用一个整数的不同二进制位来表示不同的状态,从而节省内存空间。例如,一个游戏角色可能有奔跑、跳跃、攻击等多种状态,用一个字节(8位)的整数就可以表示8种不同状态:
#include <iostream>
// 定义状态标志
const int RUNNING = 1 << 0;
const int JUMPING = 1 << 1;
const int ATTACKING = 1 << 2;int main() {int state = 0;// 角色开始奔跑state |= RUNNING;// 角色同时进行攻击state |= ATTACKING;// 检查角色是否在奔跑if (state & RUNNING) {std::cout << "角色正在奔跑" << std::endl;}// 检查角色是否在跳跃if (state & JUMPING) {std::cout << "角色正在跳跃" << std::endl;}// 检查角色是否在攻击if (state & ATTACKING) {std::cout << "角色正在攻击" << std::endl;}return 0;
}
(二)数据压缩与加密
位运算在数据压缩和加密算法中也扮演着重要角色。例如,在一些简单的加密算法里,可以利用按位异或运算的特性对数据进行加密和解密。假设密钥为一个固定整数,对数据的每个字节与密钥进行异或操作:
#include <iostream>
#include <vector>// 加密函数
std::vector<char> encrypt(const std::vector<char>& data, char key) {std::vector<char> encryptedData;for (char c : data) {encryptedData.push_back(c ^ key);}return encryptedData;
}// 解密函数
std::vector<char> decrypt(const std::vector<char>& encryptedData, char key) {return encrypt(encryptedData, key); // 异或两次回到原数据
}int main() {std::vector<char> originalData = {'h', 'e', 'l', 'l', 'o'};char key = 10;std::vector<char> encrypted = encrypt(originalData, key);std::vector<char> decrypted = decrypt(encrypted, key);std::cout << "原始数据: ";for (char c : originalData) {std::cout << c;}std::cout << std::endl;std::cout << "加密后数据: ";for (char c : encrypted) {std::cout << static_cast<int>(c) << " ";}std::cout << std::endl;std::cout << "解密后数据: ";for (char c : decrypted) {std::cout << c;}std::cout << std::endl;return 0;
}
(三)高效算法实现
在一些算法中,位运算可以显著提高运算效率。比如快速幂算法,用于计算一个数的幂次方。传统的累乘方法时间复杂度为O(n),而利用位运算的快速幂算法时间复杂度可降低到O(log n):
#include <iostream>
// 快速幂算法
long long fastPower(long long base, long long exponent) {long long result = 1;while (exponent > 0) {if (exponent & 1) {result *= base;}base *= base;exponent >>= 1;}return result;
}int main() {long long base = 3;long long exponent = 5;long long result = fastPower(base, exponent);std::cout << base << " 的 " << exponent << " 次方是: " << result << std::endl;return 0;
}
在这个算法中,通过位运算判断指数的二进制位是否为1,从而决定是否累乘当前的底数,同时通过右移指数和不断平方底数来快速计算幂次方。
位运算虽然相对复杂,但掌握它可以为C++编程带来更高的效率和更多的可能性。无论是在底层开发还是算法优化中,位运算都是不可或缺的重要工具,值得开发者深入学习和探索。同时,这些考试计算小技巧也能帮助我们在相关考试场景中更高效地答题,取得更好的成绩。
相关文章:

考试知识点位运算
深入理解位运算 在C编程的世界里,位运算作为一种直接对二进制位进行操作的运算方式,虽然不像加减乘除等算术运算那样广为人知,却在许多关键领域发挥着至关重要的作用。从底层系统开发到高效算法设计,位运算都展现出其独特的魅力与…...
-- 数据处理与可视化)
matlab快速入门(2)-- 数据处理与可视化
MATLAB的数据处理 1. 数据导入与导出 (1) 从文件读取数据 Excel 文件:data readtable(data.xlsx); % 读取为表格(Table)CSV 文件:data readtable(data.csv); % 自动处理表头和分隔符文本文件:data load(data.t…...

Kafka中文文档
文章来源:https://kafka.cadn.net.cn 什么是事件流式处理? 事件流是人体中枢神经系统的数字等价物。它是 为“永远在线”的世界奠定技术基础,在这个世界里,企业越来越多地使用软件定义 和 automated,而软件的用户更…...

Python-列表
3.1 列表是什么 在Python中,列表是一种非常重要的数据结构,用于存储一系列有序的元素。列表中的每个元素都有一个索引,索引从0开始。列表可以包含任何类型的元素,包括其他列表。 # 创建一个列表my_list [1, 2, 3, four, 5.0]…...

51单片机开发:定时器中断
目标:利用定时器中断,每隔1s开启/熄灭LED1灯。 外部中断结构图如下图所示,要使用定时器中断T0,须开启TE0、ET0。: 系统中断号如下图所示:定时器0的中断号为1。 定时器0的工作方式1原理图如下图所示&#x…...

【HarmonyOS之旅】基于ArkTS开发(三) -> 兼容JS的类Web开发(二)
目录 1 -> HML语法 1.1 -> 页面结构 1.2 -> 数据绑定 1.3 -> 普通事件绑定 1.4 -> 冒泡事件绑定5 1.5 -> 捕获事件绑定5 1.6 -> 列表渲染 1.7 -> 条件渲染 1.8 -> 逻辑控制块 1.9 -> 模板引用 2 -> CSS语法 2.1 -> 尺寸单位 …...

算法【混合背包】
混合背包是指多种背包模型的组合与转化。 下面通过题目加深理解。 题目一 测试链接:1742 -- Coins 分析:这道题可以通过硬币的个数将其转化为01背包,完全背包和多重背包。如果硬币的个数是1个,则是01背包;如果硬币的…...
)
WordPress eventon-lite插件存在未授权信息泄露漏洞(CVE-2024-0235)
免责声明: 本文旨在提供有关特定漏洞的深入信息,帮助用户充分了解潜在的安全风险。发布此信息的目的在于提升网络安全意识和推动技术进步,未经授权访问系统、网络或应用程序,可能会导致法律责任或严重后果。因此,作者不对读者基于本文内容所采取的任何行为承担责任。读者在…...

基于微信小程序的医院预约挂号系统设计与实现(LW+源码+讲解)
专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌。 技术范围:SpringBoot、Vue、SSM、HLMT、小程序、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容:…...

C++初阶 -- 手撕string类(模拟实现string类)
目录 一、string类的成员变量 二、构造函数 2.1 无参版本 2.2 有参版本 2.3 缺省值版本 三、析构函数 四、拷贝构造函数 五、c_str函数 六、operator重载 七、size函数 八、迭代器iterator 8.1 正常版本 8.2 const版本 九、operator[] 9.1 正常版本 9.2 const版…...

【Postman接口测试】Postman的安装和使用
在软件测试领域,接口测试是保障软件质量的关键环节之一,而Postman作为一款功能强大且广受欢迎的接口测试工具,能够帮助测试人员高效地进行接口测试工作。本文将详细介绍Postman的安装和使用方法,让你快速上手这款工具。 一、Pos…...
miniconda学习笔记
文章主要内容:演示miniconda切换不同python环境,安装python库,使用pycharm配置不同的conda建的python环境 目录 一、miniconda 1. 是什么? 2.安装miniconda 3.基本操作 一、miniconda 1. 是什么? miniconda是一个anac…...

区块链项目孵化与包装设计:从概念到市场的全流程指南
区块链技术的快速发展催生了大量创新项目,但如何将一个区块链项目从概念孵化成市场认可的产品,是许多团队面临的挑战。本文将从孵化策略、包装设计和市场落地三个维度,为你解析区块链项目成功的关键步骤。 一、区块链项目孵化的核心要素 明确…...

JavaScript的基本组成
1、JavaScript的组成部分 JavaScript可以分为三个部分:ECMAScript标准、DOM、BOM。 ECMAScript标准 即JS的基本语法,JavaScript的核心,描述了语言的基本语法和数据类型,ECMAScript是一套标 准,定义了一种语言…...
[Linux]从零开始的STM32MP157 U-Boot移植
一、前言 在上一次教程中,我们了解了STM32MP157的启动流程与安全启动机制。我们还将FSBL的相关代码移植成功了。大家还记得FSBL的下一个步骤是什么吗?没错,就是SSBL,而且常见的我们将SSBL作为存放U-Boot的地方。所以本次教程&…...

【Unity3D】实现横版2D游戏——攀爬绳索(简易版)
目录 GeneRope.cs 场景绳索生成类 HeroColliderController.cs 控制角色与单向平台是否忽略碰撞 HeroClampController.cs 控制角色攀爬 OnTriggerEnter2D方法 OnTriggerStay2D方法 OnTriggerExit2D方法 Update方法 开始攀爬 结束攀爬 Sensor_HeroKnight.cs 角色触发器…...

【llm对话系统】大模型 Llama 源码分析之 LoRA 微调
1. 引言 微调 (Fine-tuning) 是将预训练大模型 (LLM) 应用于下游任务的常用方法。然而,直接微调大模型的所有参数通常需要大量的计算资源和内存。LoRA (Low-Rank Adaptation) 是一种高效的微调方法,它通过引入少量可训练参数,固定预训练模型…...

算法随笔_35: 每日温度
上一篇:算法随笔_34: 最后一个单词的长度-CSDN博客 题目描述如下: 给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升…...

嵌入式硬件篇---CPUGPUTPU
文章目录 第一部分:处理器CPU(中央处理器)1.通用性2.核心数3.缓存4.指令集5.功耗和发热 GPU(图形处理器)1.并行处理2.核心数量3.内存带宽4.专门的应用 TPU(张量处理单元)1.为深度学习定制2.低精…...
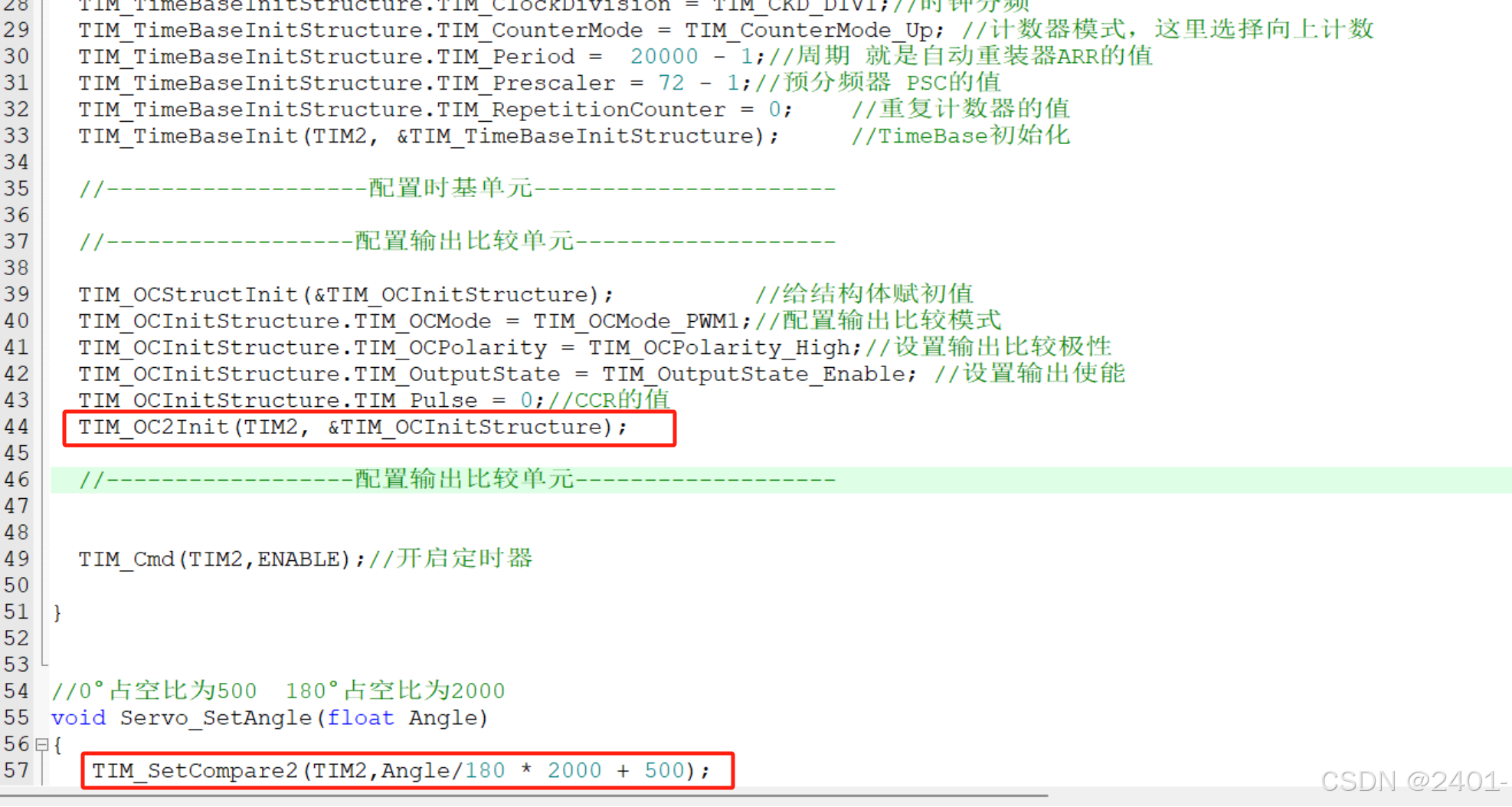
STM32 PWM驱动舵机
接线图: 这里将信号线连接到了开发板的PA1上 代码配置: 这里的PWM配置与呼吸灯一样,呼吸灯连接的是PA0引脚,输出比较单元用的是OC1通道,这里只需改为OC2通道即可。 完整代码: #include "servo.h&quo…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
