14 2D矩形模块( rect.rs)
一、 rect.rs源码
// Copyright 2013 The Servo Project Developers. See the COPYRIGHT
// file at the top-level directory of this distribution.
//
// Licensed under the Apache License, Version 2.0 <LICENSE-APACHE or
// http://www.apache.org/licenses/LICENSE-2.0> or the MIT license
// <LICENSE-MIT or http://opensource.org/licenses/MIT>, at your
// option. This file may not be copied, modified, or distributed
// except according to those terms.use super::UnknownUnit;
use crate::box2d::Box2D;
use crate::num::*;
use crate::point::Point2D;
use crate::scale::Scale;
use crate::side_offsets::SideOffsets2D;
use crate::size::Size2D;
use crate::vector::Vector2D;#[cfg(feature = "bytemuck")]
use bytemuck::{Pod, Zeroable};
use num_traits::{Float, NumCast};
#[cfg(feature = "serde")]
use serde::{Deserialize, Serialize};use core::borrow::Borrow;
use core::cmp::PartialOrd;
use core::fmt;
use core::hash::{Hash, Hasher};
use core::ops::{Add, Div, DivAssign, Mul, MulAssign, Range, Sub};/// A 2d Rectangle optionally tagged with a unit.
///
/// # Representation
///
/// `Rect` is represented by an origin point and a size.
///
/// See [`Box2D`] for a rectangle represented by two endpoints.
///
/// # Empty rectangle
///
/// A rectangle is considered empty (see [`is_empty`]) if any of the following is true:
/// - it's area is empty,
/// - it's area is negative (`size.x < 0` or `size.y < 0`),
/// - it contains NaNs.
///
/// [`is_empty`]: Self::is_empty
#[repr(C)]
#[cfg_attr(feature = "serde", derive(Serialize, Deserialize))]
#[cfg_attr(feature = "serde",serde(bound(serialize = "T: Serialize", deserialize = "T: Deserialize<'de>"))
)]
pub struct Rect<T, U> {pub origin: Point2D<T, U>,pub size: Size2D<T, U>,
}#[cfg(feature = "arbitrary")]
impl<'a, T, U> arbitrary::Arbitrary<'a> for Rect<T, U>
whereT: arbitrary::Arbitrary<'a>,
{fn arbitrary(u: &mut arbitrary::Unstructured<'a>) -> arbitrary::Result<Self> {let (origin, size) = arbitrary::Arbitrary::arbitrary(u)?;Ok(Rect { origin, size })}
}#[cfg(feature = "bytemuck")]
unsafe impl<T: Zeroable, U> Zeroable for Rect<T, U> {}#[cfg(feature = "bytemuck")]
unsafe impl<T: Pod, U: 'static> Pod for Rect<T, U> {}impl<T: Hash, U> Hash for Rect<T, U> {fn hash<H: Hasher>(&self, h: &mut H) {self.origin.hash(h);self.size.hash(h);}
}impl<T: Copy, U> Copy for Rect<T, U> {}impl<T: Clone, U> Clone for Rect<T, U> {fn clone(&self) -> Self {Self::new(self.origin.clone(), self.size.clone())}
}impl<T: PartialEq, U> PartialEq for Rect<T, U> {fn eq(&self, other: &Self) -> bool {self.origin.eq(&other.origin) && self.size.eq(&other.size)}
}impl<T: Eq, U> Eq for Rect<T, U> {}impl<T: fmt::Debug, U> fmt::Debug for Rect<T, U> {fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result {write!(f, "Rect(")?;fmt::Debug::fmt(&self.size, f)?;write!(f, " at ")?;fmt::Debug::fmt(&self.origin, f)?;write!(f, ")")}
}impl<T: Default, U> Default for Rect<T, U> {fn default() -> Self {Rect::new(Default::default(), Default::default())}
}impl<T, U> Rect<T, U> {/// Constructor.#[inline]pub const fn new(origin: Point2D<T, U>, size: Size2D<T, U>) -> Self {Rect { origin, size }}
}impl<T, U> Rect<T, U>
whereT: Zero,
{/// Constructor, setting all sides to zero.#[inline]pub fn zero() -> Self {Rect::new(Point2D::origin(), Size2D::zero())}/// Creates a rect of the given size, at offset zero.#[inline]pub fn from_size(size: Size2D<T, U>) -> Self {Rect {origin: Point2D::zero(),size,}}
}impl<T, U> Rect<T, U>
whereT: Copy + Add<T, Output = T>,
{#[inline]pub fn min(&self) -> Point2D<T, U> {self.origin}#[inline]pub fn max(&self) -> Point2D<T, U> {self.origin + self.size}#[inline]pub fn max_x(&self) -> T {self.origin.x + self.size.width}#[inline]pub fn min_x(&self) -> T {self.origin.x}#[inline]pub fn max_y(&self) -> T {self.origin.y + self.size.height}#[inline]pub fn min_y(&self) -> T {self.origin.y}#[inline]pub fn width(&self) -> T {self.size.width}#[inline]pub fn height(&self) -> T {self.size.height}#[inline]pub fn x_range(&self) -> Range<T> {self.min_x()..self.max_x()}#[inline]pub fn y_range(&self) -> Range<T> {self.min_y()..self.max_y()}/// Returns the same rectangle, translated by a vector.#[inline]#[must_use]pub fn translate(&self, by: Vector2D<T, U>) -> Self {Self::new(self.origin + by, self.size)}#[inline]pub fn to_box2d(&self) -> Box2D<T, U> {Box2D {min: self.min(),max: self.max(),}}
}impl<T, U> Rect<T, U>
whereT: Copy + PartialOrd + Add<T, Output = T>,
{/// Returns `true` if this rectangle contains the point. Points are considered/// in the rectangle if they are on the left or top edge, but outside if they/// are on the right or bottom edge.#[inline]pub fn contains(&self, p: Point2D<T, U>) -> bool {self.to_box2d().contains(p)}#[inline]pub fn intersects(&self, other: &Self) -> bool {self.to_box2d().intersects(&other.to_box2d())}
}impl<T, U> Rect<T, U>
whereT: Copy + PartialOrd + Add<T, Output = T> + Sub<T, Output = T>,
{#[inline]pub fn intersection(&self, other: &Self) -> Option<Self> {let box2d = self.to_box2d().intersection_unchecked(&other.to_box2d());if box2d.is_empty() {return None;}Some(box2d.to_rect())}
}impl<T, U> Rect<T, U>
whereT: Copy + Add<T, Output = T> + Sub<T, Output = T>,
{#[inline]#[must_use]pub fn inflate(&self, width: T, height: T) -> Self {Rect::new(Point2D::new(self.origin.x - width, self.origin.y - height),Size2D::new(self.size.width + width + width,self.size.height + height + height,),)}
}impl<T, U> Rect<T, U>
whereT: Copy + Zero + PartialOrd + Add<T, Output = T>,
{/// Returns `true` if this rectangle contains the interior of `rect`. Always/// returns `true` if `rect` is empty, and always returns `false` if `rect` is/// nonempty but this rectangle is empty.#[inline]pub fn contains_rect(&self, rect: &Self) -> bool {rect.is_empty()|| (self.min_x() <= rect.min_x()&& rect.max_x() <= self.max_x()&& self.min_y() <= rect.min_y()&& rect.max_y() <= self.max_y())}
}impl<T, U> Rect<T, U>
whereT: Copy + Zero + PartialOrd + Add<T, Output = T> + Sub<T, Output = T>,
{/// Calculate the size and position of an inner rectangle.////// Subtracts the side offsets from all sides. The horizontal and vertical/// offsets must not be larger than the original side length./// This method assumes y oriented downward.pub fn inner_rect(&self, offsets: SideOffsets2D<T, U>) -> Self {let rect = Rect::new(Point2D::new(self.origin.x + offsets.left, self.origin.y + offsets.top),Size2D::new(self.size.width - offsets.horizontal(),self.size.height - offsets.vertical(),),);debug_assert!(rect.size.width >= Zero::zero());debug_assert!(rect.size.height >= Zero::zero());rect}
}impl<T, U> Rect<T, U>
whereT: Copy + Add<T, Output = T> + Sub<T, Output = T>,
{/// Calculate the size and position of an outer rectangle.////// Add the offsets to all sides. The expanded rectangle is returned./// This method assumes y oriented downward.pub fn outer_rect(&self, offsets: SideOffsets2D<T, U>) -> Self {Rect::new(Point2D::new(self.origin.x - offsets.left, self.origin.y - offsets.top),Size2D::new(self.size.width + offsets.horizontal(),self.size.height + offsets.vertical(),),)}
}impl<T, U> Rect<T, U>
whereT: Copy + Zero + PartialOrd + Sub<T, Output = T>,
{/// Returns the smallest rectangle defined by the top/bottom/left/right-most/// points provided as parameter.////// Note: This function has a behavior that can be surprising because/// the right-most and bottom-most points are exactly on the edge/// of the rectangle while the [`Rect::contains`] function is has exclusive/// semantic on these edges. This means that the right-most and bottom-most/// points provided to [`Rect::from_points`] will count as not contained by the rect./// This behavior may change in the future.////// See [`Box2D::from_points`] for more details.pub fn from_points<I>(points: I) -> SelfwhereI: IntoIterator,I::Item: Borrow<Point2D<T, U>>,{Box2D::from_points(points).to_rect()}
}impl<T, U> Rect<T, U>
whereT: Copy + One + Add<Output = T> + Sub<Output = T> + Mul<Output = T>,
{/// Linearly interpolate between this rectangle and another rectangle.#[inline]pub fn lerp(&self, other: Self, t: T) -> Self {Self::new(self.origin.lerp(other.origin, t),self.size.lerp(other.size, t),)}
}impl<T, U> Rect<T, U>
whereT: Copy + One + Add<Output = T> + Div<Output = T>,
{pub fn center(&self) -> Point2D<T, U> {let two = T::one() + T::one();self.origin + self.size.to_vector() / two}
}impl<T, U> Rect<T, U>
whereT: Copy + PartialOrd + Add<T, Output = T> + Sub<T, Output = T> + Zero,
{#[inline]pub fn union(&self, other: &Self) -> Self {self.to_box2d().union(&other.to_box2d()).to_rect()}
}impl<T, U> Rect<T, U> {#[inline]pub fn scale<S: Copy>(&self, x: S, y: S) -> SelfwhereT: Copy + Mul<S, Output = T>,{Rect::new(Point2D::new(self.origin.x * x, self.origin.y * y),Size2D::new(self.size.width * x, self.size.height * y),)}
}impl<T: Copy + Mul<T, Output = T>, U> Rect<T, U> {#[inline]pub fn area(&self) -> T {self.size.area()}
}impl<T: Copy + Zero + PartialOrd, U> Rect<T, U> {#[inline]pub fn is_empty(&self) -> bool {self.size.is_empty()}
}impl<T: Copy + Zero + PartialOrd, U> Rect<T, U> {#[inline]pub fn to_non_empty(&self) -> Option<Self> {if self.is_empty() {return None;}Some(*self)}
}impl<T: Copy + Mul, U> Mul<T> for Rect<T, U> {type Output = Rect<T::Output, U>;#[inline]fn mul(self, scale: T) -> Self::Output {Rect::new(self.origin * scale, self.size * scale)}
}impl<T: Copy + MulAssign, U> MulAssign<T> for Rect<T, U> {#[inline]fn mul_assign(&mut self, scale: T) {*self *= Scale::new(scale);}
}impl<T: Copy + Div, U> Div<T> for Rect<T, U> {type Output = Rect<T::Output, U>;#[inline]fn div(self, scale: T) -> Self::Output {Rect::new(self.origin / scale.clone(), self.size / scale)}
}impl<T: Copy + DivAssign, U> DivAssign<T> for Rect<T, U> {#[inline]fn div_assign(&mut self, scale: T) {*self /= Scale::new(scale);}
}impl<T: Copy + Mul, U1, U2> Mul<Scale<T, U1, U2>> for Rect<T, U1> {type Output = Rect<T::Output, U2>;#[inline]fn mul(self, scale: Scale<T, U1, U2>) -> Self::Output {Rect::new(self.origin * scale.clone(), self.size * scale)}
}impl<T: Copy + MulAssign, U> MulAssign<Scale<T, U, U>> for Rect<T, U> {#[inline]fn mul_assign(&mut self, scale: Scale<T, U, U>) {self.origin *= scale.clone();self.size *= scale;}
}impl<T: Copy + Div, U1, U2> Div<Scale<T, U1, U2>> for Rect<T, U2> {type Output = Rect<T::Output, U1>;#[inline]fn div(self, scale: Scale<T, U1, U2>) -> Self::Output {Rect::new(self.origin / scale.clone(), self.size / scale)}
}impl<T: Copy + DivAssign, U> DivAssign<Scale<T, U, U>> for Rect<T, U> {#[inline]fn div_assign(&mut self, scale: Scale<T, U, U>) {self.origin /= scale.clone();self.size /= scale;}
}impl<T: Copy, U> Rect<T, U> {/// Drop the units, preserving only the numeric value.#[inline]pub fn to_untyped(&self) -> Rect<T, UnknownUnit> {Rect::new(self.origin.to_untyped(), self.size.to_untyped())}/// Tag a unitless value with units.#[inline]pub fn from_untyped(r: &Rect<T, UnknownUnit>) -> Rect<T, U> {Rect::new(Point2D::from_untyped(r.origin),Size2D::from_untyped(r.size),)}/// Cast the unit#[inline]pub fn cast_unit<V>(&self) -> Rect<T, V> {Rect::new(self.origin.cast_unit(), self.size.cast_unit())}
}impl<T: NumCast + Copy, U> Rect<T, U> {/// Cast from one numeric representation to another, preserving the units.////// When casting from floating point to integer coordinates, the decimals are truncated/// as one would expect from a simple cast, but this behavior does not always make sense/// geometrically. Consider using [`round`], [`round_in`] or [`round_out`] before casting.////// [`round`]: Self::round/// [`round_in`]: Self::round_in/// [`round_out`]: Self::round_out#[inline]pub fn cast<NewT: NumCast>(&self) -> Rect<NewT, U> {Rect::new(self.origin.cast(), self.size.cast())}/// Fallible cast from one numeric representation to another, preserving the units.////// When casting from floating point to integer coordinates, the decimals are truncated/// as one would expect from a simple cast, but this behavior does not always make sense/// geometrically. Consider using [`round`], [`round_in`] or [`round_out` before casting.////// [`round`]: Self::round/// [`round_in`]: Self::round_in/// [`round_out`]: Self::round_outpub fn try_cast<NewT: NumCast>(&self) -> Option<Rect<NewT, U>> {match (self.origin.try_cast(), self.size.try_cast()) {(Some(origin), Some(size)) => Some(Rect::new(origin, size)),_ => None,}}// Convenience functions for common casts/// Cast into an `f32` rectangle.#[inline]pub fn to_f32(&self) -> Rect<f32, U> {self.cast()}/// Cast into an `f64` rectangle.#[inline]pub fn to_f64(&self) -> Rect<f64, U> {self.cast()}/// Cast into an `usize` rectangle, truncating decimals if any.////// When casting from floating point rectangles, it is worth considering whether/// to `round()`, `round_in()` or `round_out()` before the cast in order to/// obtain the desired conversion behavior.#[inline]pub fn to_usize(&self) -> Rect<usize, U> {self.cast()}/// Cast into an `u32` rectangle, truncating decimals if any.////// When casting from floating point rectangles, it is worth considering whether/// to `round()`, `round_in()` or `round_out()` before the cast in order to/// obtain the desired conversion behavior.#[inline]pub fn to_u32(&self) -> Rect<u32, U> {self.cast()}/// Cast into an `u64` rectangle, truncating decimals if any.////// When casting from floating point rectangles, it is worth considering whether/// to `round()`, `round_in()` or `round_out()` before the cast in order to/// obtain the desired conversion behavior.#[inline]pub fn to_u64(&self) -> Rect<u64, U> {self.cast()}/// Cast into an `i32` rectangle, truncating decimals if any.////// When casting from floating point rectangles, it is worth considering whether/// to `round()`, `round_in()` or `round_out()` before the cast in order to/// obtain the desired conversion behavior.#[inline]pub fn to_i32(&self) -> Rect<i32, U> {self.cast()}/// Cast into an `i64` rectangle, truncating decimals if any.////// When casting from floating point rectangles, it is worth considering whether/// to `round()`, `round_in()` or `round_out()` before the cast in order to/// obtain the desired conversion behavior.#[inline]pub fn to_i64(&self) -> Rect<i64, U> {self.cast()}
}impl<T: Float, U> Rect<T, U> {/// Returns `true` if all members are finite.#[inline]pub fn is_finite(self) -> bool {self.origin.is_finite() && self.size.is_finite()}
}impl<T: Floor + Ceil + Round + Add<T, Output = T> + Sub<T, Output = T>, U> Rect<T, U> {/// Return a rectangle with edges rounded to integer coordinates, such that/// the returned rectangle has the same set of pixel centers as the original/// one./// Edges at offset 0.5 round up./// Suitable for most places where integral device coordinates/// are needed, but note that any translation should be applied first to/// avoid pixel rounding errors./// Note that this is *not* rounding to nearest integer if the values are negative./// They are always rounding as floor(n + 0.5).////// # Usage notes/// Note, that when using with floating-point `T` types that method can significantly/// lose precision for large values, so if you need to call this method very often it/// is better to use [`Box2D`].#[must_use]pub fn round(&self) -> Self {self.to_box2d().round().to_rect()}/// Return a rectangle with edges rounded to integer coordinates, such that/// the original rectangle contains the resulting rectangle.////// # Usage notes/// Note, that when using with floating-point `T` types that method can significantly/// lose precision for large values, so if you need to call this method very often it/// is better to use [`Box2D`].#[must_use]pub fn round_in(&self) -> Self {self.to_box2d().round_in().to_rect()}/// Return a rectangle with edges rounded to integer coordinates, such that/// the original rectangle is contained in the resulting rectangle.////// # Usage notes/// Note, that when using with floating-point `T` types that method can significantly/// lose precision for large values, so if you need to call this method very often it/// is better to use [`Box2D`].#[must_use]pub fn round_out(&self) -> Self {self.to_box2d().round_out().to_rect()}
}impl<T, U> From<Size2D<T, U>> for Rect<T, U>
whereT: Zero,
{fn from(size: Size2D<T, U>) -> Self {Self::from_size(size)}
}/// Shorthand for `Rect::new(Point2D::new(x, y), Size2D::new(w, h))`.
pub const fn rect<T, U>(x: T, y: T, w: T, h: T) -> Rect<T, U> {Rect::new(Point2D::new(x, y), Size2D::new(w, h))
}#[cfg(test)]
mod tests {use crate::default::{Point2D, Rect, Size2D};use crate::side_offsets::SideOffsets2D;use crate::{point2, rect, size2, vec2};#[test]fn test_translate() {let p = Rect::new(Point2D::new(0u32, 0u32), Size2D::new(50u32, 40u32));let pp = p.translate(vec2(10, 15));assert!(pp.size.width == 50);assert!(pp.size.height == 40);assert!(pp.origin.x == 10);assert!(pp.origin.y == 15);let r = Rect::new(Point2D::new(-10, -5), Size2D::new(50, 40));let rr = r.translate(vec2(0, -10));assert!(rr.size.width == 50);assert!(rr.size.height == 40);assert!(rr.origin.x == -10);assert!(rr.origin.y == -15);}#[test]fn test_union() {let p = Rect::new(Point2D::new(0, 0), Size2D::new(50, 40));let q = Rect::new(Point2D::new(20, 20), Size2D::new(5, 5));let r = Rect::new(Point2D::new(-15, -30), Size2D::new(200, 15));let s = Rect::new(Point2D::new(20, -15), Size2D::new(250, 200));let pq = p.union(&q);assert!(pq.origin == Point2D::new(0, 0));assert!(pq.size == Size2D::new(50, 40));let pr = p.union(&r);assert!(pr.origin == Point2D::new(-15, -30));assert!(pr.size == Size2D::new(200, 70));let ps = p.union(&s);assert!(ps.origin == Point2D::new(0, -15));assert!(ps.size == Size2D::new(270, 200));}#[test]fn test_intersection() {let p = Rect::new(Point2D::new(0, 0), Size2D::new(10, 20));let q = Rect::new(Point2D::new(5, 15), Size2D::new(10, 10));let r = Rect::new(Point2D::new(-5, -5), Size2D::new(8, 8));let pq = p.intersection(&q);assert!(pq.is_some());let pq = pq.unwrap();assert!(pq.origin == Point2D::new(5, 15));assert!(pq.size == Size2D::new(5, 5));let pr = p.intersection(&r);assert!(pr.is_some());let pr = pr.unwrap();assert!(pr.origin == Point2D::new(0, 0));assert!(pr.size == Size2D::new(3, 3));let qr = q.intersection(&r);assert!(qr.is_none());}#[test]fn test_intersection_overflow() {// test some scenarios where the intersection can overflow but// the min_x() and max_x() don't. Gecko currently fails these caseslet p = Rect::new(Point2D::new(-2147483648, -2147483648), Size2D::new(0, 0));let q = Rect::new(Point2D::new(2136893440, 2136893440),Size2D::new(279552, 279552),);let r = Rect::new(Point2D::new(-2147483648, -2147483648), Size2D::new(1, 1));assert!(p.is_empty());let pq = p.intersection(&q);assert!(pq.is_none());let qr = q.intersection(&r);assert!(qr.is_none());}#[test]fn test_contains() {let r = Rect::new(Point2D::new(-20, 15), Size2D::new(100, 200));assert!(r.contains(Point2D::new(0, 50)));assert!(r.contains(Point2D::new(-10, 200)));// The `contains` method is inclusive of the top/left edges, but not the// bottom/right edges.assert!(r.contains(Point2D::new(-20, 15)));assert!(!r.contains(Point2D::new(80, 15)));assert!(!r.contains(Point2D::new(80, 215)));assert!(!r.contains(Point2D::new(-20, 215)));// Points beyond the top-left corner.assert!(!r.contains(Point2D::new(-25, 15)));assert!(!r.contains(Point2D::new(-15, 10)));// Points beyond the top-right corner.assert!(!r.contains(Point2D::new(85, 20)));assert!(!r.contains(Point2D::new(75, 10)));// Points beyond the bottom-right corner.assert!(!r.contains(Point2D::new(85, 210)));assert!(!r.contains(Point2D::new(75, 220)));// Points beyond the bottom-left corner.assert!(!r.contains(Point2D::new(-25, 210)));assert!(!r.contains(Point2D::new(-15, 220)));let r = Rect::new(Point2D::new(-20.0, 15.0), Size2D::new(100.0, 200.0));assert!(r.contains_rect(&r));assert!(!r.contains_rect(&r.translate(vec2(0.1, 0.0))));assert!(!r.contains_rect(&r.translate(vec2(-0.1, 0.0))));assert!(!r.contains_rect(&r.translate(vec2(0.0, 0.1))));assert!(!r.contains_rect(&r.translate(vec2(0.0, -0.1))));// Empty rectangles are always considered as contained in other rectangles,// even if their origin is not.let p = Point2D::new(1.0, 1.0);assert!(!r.contains(p));assert!(r.contains_rect(&Rect::new(p, Size2D::zero())));}#[test]fn test_scale() {let p = Rect::new(Point2D::new(0u32, 0u32), Size2D::new(50u32, 40u32));let pp = p.scale(10, 15);assert!(pp.size.width == 500);assert!(pp.size.height == 600);assert!(pp.origin.x == 0);assert!(pp.origin.y == 0);let r = Rect::new(Point2D::new(-10, -5), Size2D::new(50, 40));let rr = r.scale(1, 20);assert!(rr.size.width == 50);assert!(rr.size.height == 800);assert!(rr.origin.x == -10);assert!(rr.origin.y == -100);}#[test]fn test_inflate() {let p = Rect::new(Point2D::new(0, 0), Size2D::new(10, 10));let pp = p.inflate(10, 20);assert!(pp.size.width == 30);assert!(pp.size.height == 50);assert!(pp.origin.x == -10);assert!(pp.origin.y == -20);let r = Rect::new(Point2D::new(0, 0), Size2D::new(10, 20));let rr = r.inflate(-2, -5);assert!(rr.size.width == 6);assert!(rr.size.height == 10);assert!(rr.origin.x == 2);assert!(rr.origin.y == 5);}#[test]fn test_inner_outer_rect() {let inner_rect = Rect::new(point2(20, 40), size2(80, 100));let offsets = SideOffsets2D::new(20, 10, 10, 10);let outer_rect = inner_rect.outer_rect(offsets);assert_eq!(outer_rect.origin.x, 10);assert_eq!(outer_rect.origin.y, 20);assert_eq!(outer_rect.size.width, 100);assert_eq!(outer_rect.size.height, 130);assert_eq!(outer_rect.inner_rect(offsets), inner_rect);}#[test]fn test_min_max_x_y() {let p = Rect::new(Point2D::new(0u32, 0u32), Size2D::new(50u32, 40u32));assert!(p.max_y() == 40);assert!(p.min_y() == 0);assert!(p.max_x() == 50);assert!(p.min_x() == 0);let r = Rect::new(Point2D::new(-10, -5), Size2D::new(50, 40));assert!(r.max_y() == 35);assert!(r.min_y() == -5);assert!(r.max_x() == 40);assert!(r.min_x() == -10);}#[test]fn test_width_height() {let r = Rect::new(Point2D::new(-10, -5), Size2D::new(50, 40));assert!(r.width() == 50);assert!(r.height() == 40);}#[test]fn test_is_empty() {assert!(Rect::new(Point2D::new(0u32, 0u32), Size2D::new(0u32, 0u32)).is_empty());assert!(Rect::new(Point2D::new(0u32, 0u32), Size2D::new(10u32, 0u32)).is_empty());assert!(Rect::new(Point2D::new(0u32, 0u32), Size2D::new(0u32, 10u32)).is_empty());assert!(!Rect::new(Point2D::new(0u32, 0u32), Size2D::new(1u32, 1u32)).is_empty());assert!(Rect::new(Point2D::new(10u32, 10u32), Size2D::new(0u32, 0u32)).is_empty());assert!(Rect::new(Point2D::new(10u32, 10u32), Size2D::new(10u32, 0u32)).is_empty());assert!(Rect::new(Point2D::new(10u32, 10u32), Size2D::new(0u32, 10u32)).is_empty());assert!(!Rect::new(Point2D::new(10u32, 10u32), Size2D::new(1u32, 1u32)).is_empty());}#[test]fn test_round() {let mut x = -2.0;let mut y = -2.0;let mut w = -2.0;let mut h = -2.0;while x < 2.0 {while y < 2.0 {while w < 2.0 {while h < 2.0 {let rect = Rect::new(Point2D::new(x, y), Size2D::new(w, h));assert!(rect.contains_rect(&rect.round_in()));assert!(rect.round_in().inflate(1.0, 1.0).contains_rect(&rect));assert!(rect.round_out().contains_rect(&rect));assert!(rect.inflate(1.0, 1.0).contains_rect(&rect.round_out()));assert!(rect.inflate(1.0, 1.0).contains_rect(&rect.round()));assert!(rect.round().inflate(1.0, 1.0).contains_rect(&rect));h += 0.1;}w += 0.1;}y += 0.1;}x += 0.1;}}#[test]fn test_center() {let r: Rect<i32> = rect(-2, 5, 4, 10);assert_eq!(r.center(), point2(0, 10));let r: Rect<f32> = rect(1.0, 2.0, 3.0, 4.0);assert_eq!(r.center(), point2(2.5, 4.0));}#[test]fn test_nan() {let r1: Rect<f32> = rect(-2.0, 5.0, 4.0, std::f32::NAN);let r2: Rect<f32> = rect(std::f32::NAN, -1.0, 3.0, 10.0);assert_eq!(r1.intersection(&r2), None);}
}相关文章:
)
14 2D矩形模块( rect.rs)
一、 rect.rs源码 // Copyright 2013 The Servo Project Developers. See the COPYRIGHT // file at the top-level directory of this distribution. // // Licensed under the Apache License, Version 2.0 <LICENSE-APACHE or // http://www.apache.org/licenses/LICENS…...
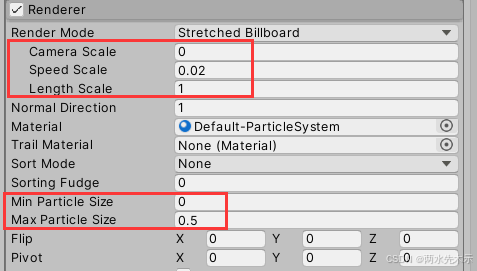
【Unity3D】实现2D角色/怪物死亡消散粒子效果
核心:这是一个Unity粒子系统自带的一种功能,可将粒子生成控制在一个Texture图片网格范围内,并且粒子颜色会自动采样图片的像素点颜色,之后则是粒子编辑出消散效果。 Particle System1物体(爆发式随机速度扩散10000个粒…...
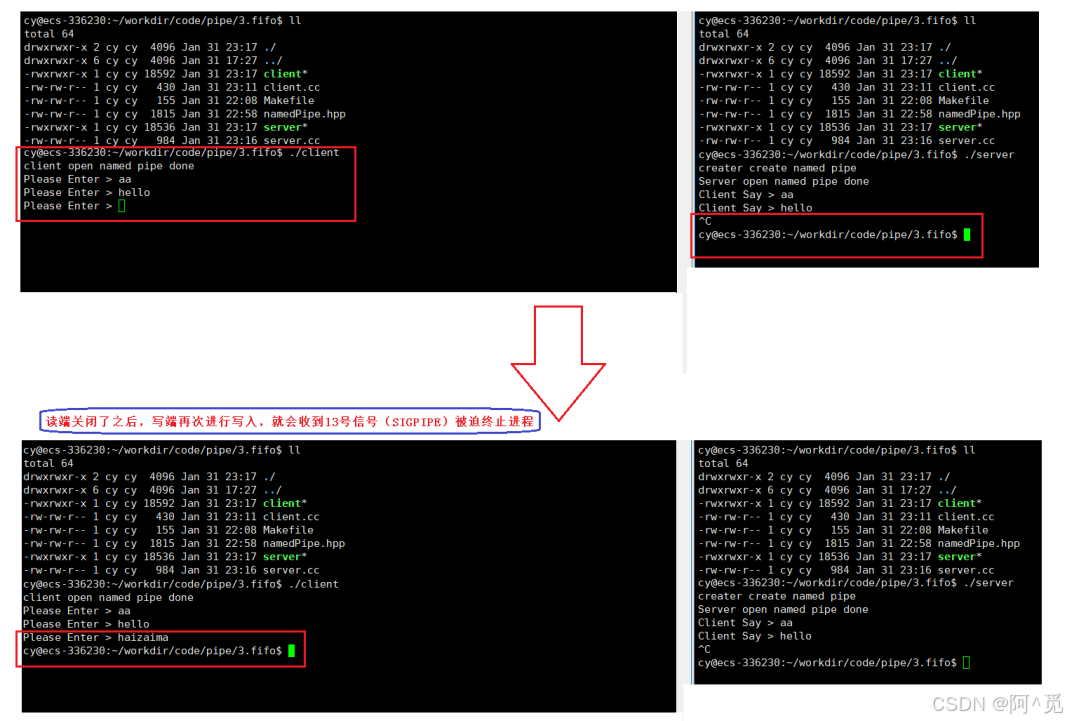
Linux - 进程间通信(3)
目录 3、解决遗留BUG -- 边关闭信道边回收进程 1)解决方案 2)两种方法相比较 4、命名管道 1)理解命名管道 2)创建命名管道 a. 命令行指令 b. 系统调用方法 3)代码实现命名管道 构建类进行封装命名管道&#…...
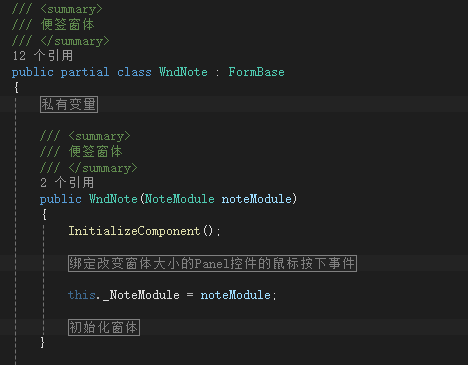
3、C#基于.net framework的应用开发实战编程 - 实现(三、三) - 编程手把手系列文章...
三、 实现; 三.三、编写应用程序; 此文主要是实现应用的主要编码工作。 1、 分层; 此例子主要分为UI、Helper、DAL等层。UI负责便签的界面显示;Helper主要是链接UI和数据库操作的中间层;DAL为对数据库的操…...
)
C++编程语言:抽象机制:泛型编程(Bjarne Stroustrup)
泛型编程(Generic Programming) 目录 24.1 引言(Introduction) 24.2 算法和(通用性的)提升(Algorithms and Lifting) 24.3 概念(此指模板参数的插件)(Concepts) 24.3.1 发现插件集(Discovering a Concept) 24.3.2 概念与约束(Concepts and Constraints) 24.4 具体化…...

Python面试宝典13 | Python 变量作用域,从入门到精通
今天,我们来深入探讨一下 Python 中一个非常重要的概念——变量作用域。理解变量作用域对于编写清晰、可维护、无 bug 的代码至关重要。 什么是变量作用域? 简单来说,变量作用域就是指一个变量在程序中可以被访问的范围。Python 中有四种作…...

基于最近邻数据进行分类
人工智能例子汇总:AI常见的算法和例子-CSDN博客 完整代码: import torch import numpy as np from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import accuracy_score import matplotlib.pyplot as plt# 生成一个简单的数据…...

DeepSeek V3 vs R1:大模型技术路径的“瑞士军刀“与“手术刀“进化
DeepSeek V3 vs R1:——大模型技术路径的"瑞士军刀"与"手术刀"进化 大模型分水岭:从通用智能到垂直突破 2023年,GPT-4 Turbo的发布标志着通用大模型进入性能瓶颈期。当模型参数量突破万亿级门槛后,研究者们开…...
一、TensorFlow的建模流程
1. 数据准备与预处理: 加载数据:使用内置数据集或自定义数据。 预处理:归一化、调整维度、数据增强。 划分数据集:训练集、验证集、测试集。 转换为Dataset对象:利用tf.data优化数据流水线。 import tensorflow a…...

指导初学者使用Anaconda运行GitHub上One - DM项目的步骤
以下是指导初学者使用Anaconda运行GitHub上One - DM项目的步骤: 1. 安装Anaconda 下载Anaconda: 让初学者访问Anaconda官网(https://www.anaconda.com/products/distribution),根据其操作系统(Windows、M…...

7层还是4层?网络模型又为什么要分层?
~犬📰余~ “我欲贱而贵,愚而智,贫而富,可乎? 曰:其唯学乎” 一、为什么要分层 \quad 网络通信的复杂性促使我们需要一种分层的方法来理解和管理网络。就像建筑一样,我们不会把所有功能都混在一起…...

C++:抽象类习题
题目内容: 求正方体、球、圆柱的表面积,抽象出一个公共的基类Container为抽象类,在其中定义一个公共的数据成员radius(此数据可以作为正方形的边长、球的半径、圆柱体底面圆半径),以及求表面积的纯虚函数area()。由此抽象类派生出…...
)
C++ 泛型编程指南02 (模板参数的类型推导)
文章目录 一 深入了解C中的函数模板类型推断什么是类型推断?使用Boost TypeIndex库进行类型推断分析示例代码关键点解析 2. 理解函数模板类型推断2.1 指针或引用类型2.1.1 忽略引用2.1.2 保持const属性2.1.3 处理指针类型 2.2 万能引用类型2.3 传值方式2.4 传值方式…...
——FFmpeg源码中,解析SDP的实现)
音视频入门基础:RTP专题(5)——FFmpeg源码中,解析SDP的实现
一、引言 FFmpeg源码中通过ff_sdp_parse函数解析SDP。该函数定义在libavformat/rtsp.c中: int ff_sdp_parse(AVFormatContext *s, const char *content) {const char *p;int letter, i;char buf[SDP_MAX_SIZE], *q;SDPParseState sdp_parse_state { { 0 } }, *s1…...

计算机网络 应用层 笔记 (电子邮件系统,SMTP,POP3,MIME,IMAP,万维网,HTTP,html)
电子邮件系统: SMTP协议 基本概念 工作原理 连接建立: 命令交互 客户端发送命令: 服务器响应: 邮件传输: 连接关闭: 主要命令 邮件发送流程 SMTP的缺点: MIME: POP3协议 基本概念…...

【视频+图文详解】HTML基础3-html常用标签
图文教程 html常用标签 常用标签 1. 文档结构 <!DOCTYPE html>:声明HTML文档类型。<html>:定义HTML文档的根元素。<head>:定义文档头部,包含元数据。<title>:设置网页标题,浏览…...

FreeRTOS学习 --- 消息队列
队列简介 队列是任务到任务、任务到中断、中断到任务数据交流的一种机制(消息传递) 全局变量的弊端:数据无保护,导致数据不安全,当多个任务同时对该变量操作时,数据易受损 使用队列的情况如下:…...

PHP If...Else 语句详解
PHP If...Else 语句详解 引言 在PHP编程中,if...else语句是流程控制的重要组成部分,它允许程序根据条件判断执行不同的代码块。本文将详细解析PHP中的if...else语句,包括其基本用法、高级技巧以及注意事项。 一、基本用法 if...else语句的…...

pytorch使用SVM实现文本分类
人工智能例子汇总:AI常见的算法和例子-CSDN博客 完整代码: import torch import torch.nn as nn import torch.optim as optim import jieba import numpy as np from sklearn.model_selection import train_test_split from sklearn.feature_extract…...
读取手机通讯录【Android移动开发基础案例教程(第2版)黑马程序员】)
安卓(android)读取手机通讯录【Android移动开发基础案例教程(第2版)黑马程序员】
一、实验目的(如果代码有错漏,可在代码地址查看) 1.熟悉内容提供者(Content Provider)的概念和作用。 2.掌握内容提供者的创建和使用方法。 4.掌握内容URI的结构和用途。 二、实验条件 1.熟悉内容提供者的工作原理。 2.掌握内容提供者访问其…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
