【优先算法】专题——前缀和

目录

一、【模版】前缀和

参考代码：

二、【模版】 二维前缀和

参考代码：

三、寻找数组的中心下标

参考代码：

四、除自身以外数组的乘积

参考代码：

五、和为K的子数组

参考代码：

六、和可被K整除的子数组

参考代码：

七、连续数组

参考代码：

八、矩阵区域和

参考代码：

总结

---

一、【模版】前缀和

【模版】前缀和

题目描述：

数组的元素是从标为1开始的，n是数组的个数，q是查询的次数，查询l到r这段区间的和。

解法一：暴力解法，直接查找l到r这段区间之和，但是效率太低，查询q次每次遍历一遍数组时间复杂度O(q*N)n和q的数据范围是1到10^5，暴力解法过不了。

解法二：前缀和，快速求出数组中某一个连续区间的和，时间复杂度O(q)+O(N)

第一步：预处理出来一个前缀和数组，我们要要求1到3的和我们用dp[i-1]+arr[i]就是1到3的和了。

dp[i]表示：表示[1,i]区间内所有元素的和。

dp[i] = dp[i-1] + arr[i]

第二步：使用前缀和数组

如下比如我们要查找l~r这段区间的和那么我们直接去dp数组取出下标为r的这个元素，此元素就是1~r的之和我们减去l-1得到的就是l~r这段区间之和。

这里还有一个问题就是为什么下标要从1开始计数：为了处理边界情况

初始化：添加虚拟结点（辅助结点）

参考代码：

#include <iostream>
#include <vector>
using namespace std;int main() 
{//1.读入数据int n,q;cin>>n>>q;vector<int>arr(n+1);for(int i = 1;i<= n;i++) cin>>arr[i];//2.预处理出来一个前缀和数组vector<long long>dp(n+1); //防止溢出for(int i = 0;i<=n;i++) dp[i] = dp[i-1] + arr[i];//3.使用前缀和数组int l,r;while(q--){cin>>l>>r;cout<<dp[r] -dp[l-1]<<endl;}}

时间复杂度：O(q)+O(n) 

---

二、【模版】 二维前缀和

题目链接：二维前缀和

题目描述：

题目解析： 

1.从第一行第一列开始到第二列，到二行二列。（如下）

2.从第一行第一列开始到第三列，到三行三列。

3.从第一行第二列开始到4列，到三行四列。

算法原理：

解法一：暴力解法,模拟，让我求哪段区间我就加到哪段区间，如下比如让我们全部求出来那就从头加到尾，时间复杂度高，这道题过不了因为时间复杂度为O(n*m*q)

解法二：前缀和

1.预处理出来一个前缀和矩阵

dp[i][j]表示：从[1,1]位置到[i,j]位置，这段区间里面所有元素和。

如下图我们把它抽象出来，这里我们分为四块面积分别为A、B、C、D，我们要求得dp[i][j]这段区间的和，我们A+B+C+D就等于dp[i][j]，我们求B和C这段区间的和是不太好求的，所以我们这样求(A+B) + (A + C) + D - A这里减A是因为多算了一个A所以要减掉，A+B这段区间的值非常好求就是dp[i-1][j]这个位置，A+C就是dp[i][j-1]再加上D这个位置的值就是数组里面的arr[i][j]减去A也就是dp[i-1][j-1]，这样就推出了我们预处理的公式。如下图：

2.使用前缀和矩阵

如下假如我们要求D这段区间的和那么我们又被分成了四个部分，竟然要求D这段区间的和我们就A+B+C+D求得结果之后我们先减去上面这部分就是A+B这部分因为A+B这部分可以直接算出了，也就是下图绿色小方块那个位置，在减去A+C这部分但是这样我们发现多减了一个A所以我们要加上一个A，D = A+B+C+D - (A+B)-(A+C)+A(通分之后就等于D)，A+B+C+D其实就等于dp[x2][y2]然后减去A+B也就是dp[x1 - 1][y2]再减去A+C也就是dp[x2][y1-1]在加上A也就是dp[x1-1][y1-1]，我们直接套用公式就能用O(1)的时间复杂度得出结果。

参考代码：

#include <iostream>
#include <vector>
using namespace std;int main() 
{//1.读入数据int n = 0,m = 0,q = 0;cin>>n>>m>>q;vector<vector<long long>>arr(n+1,vector<long long>(m+1));for(int i = 1;i <=n;i++)for(int j = 1;j <=m ;j++)cin>>arr[i][j];//2.预处理前缀和矩阵vector<vector<long long>>dp(n+1,vector<long long>(m+1));//防止溢出for(int i = 1; i<=n; i++)for(int j = 1; j<=m ;j++)dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];//3.使用前缀和矩阵int x1=0,y1=0,x2=0,y2=0;while(q--){cin>> x1 >> y1 >> x2 >>y2;cout<<dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]<<endl;}return 0;}

时间复杂为：O(n*m) + O(q)

---

三、寻找数组的中心下标

题目链接：寻找数组的中心下标

题目描述：

题目解析： 

如下图两边都等于11那么就返回6的下标，如果全是0那么就返回最左边的下标也就是0因为有多个中心下标，不存在则返回-1

解法一：暴力解法，枚举中心下标左边相加的值是否等于右边相加的值，每次枚举一次中心下标都要左边相加右边相加，枚举下标时间复杂O(N)，求和依旧使用O(N)的时间复杂度，最终时间复杂度O(N^2)。

解法二：前缀和

我们利用前缀和的思想来实现，竟然要求某一段区间的和那么前缀和预处理出来的那个数组不就可以，我们还要求后面那一段区间的和我们把前缀和改一下改成后缀和就可以了。

我们用f来表示前缀和数组：f[i]表示：[0,i-1]区间，所有元素的和。

f [i]  = f [i-1] + nums[i-1]

g：后缀和数组：g[i]表示：[i+1,n-1]区间，所有元素的和

g [i] = g [i+1] + nums[i+1]

最后进行判断，枚举所有的中心下标从0~n-1然后判断f[i] == g[i]，如果有很多中心下标要返回最左边的，所以我们枚举所有的中心下标i，然后判断f[i] == g[i]，因为f[i]表示的就是左边所有元素的和g[i]保存的就是右边所有元素的和，判断是否相等如果相等返回i不相等继续往后面找，找到最后一个位置依旧没找到就返回-1

细节问题：

当我们的f等于0的时候我们代入上面发现会越界访问，0~-1这里没有元素所以f(0)= 0

当g等于n-1的时候我们代入上面也会发生越界访问，n-1的右边是没有任何元素的所以g(0) = 0

填写元素顺序，f表是正着填的从左到右，g表是倒着填的从右到左

参考代码：

class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int>f(n),g(n);//1.预处理前缀和数组以及后缀和数组for(int i = 1;i<n;i++)f[i] = f[i-1] + nums[i-1];for(int j = n-2;j>= 0;j--)g[j] = g[j + 1] + nums[j+1];//2.使用for(int i = 0;i<n;i++){if(f[i] == g[i])return i;}return -1;}
};

时间复杂度：O(N)

---

四、除自身以外数组的乘积

题目链接：除自身以外数组的乘积

题目描述：

举个例子： 

除1以为2*3*4等于24，除2以外1*3*4等于12，除3以为1*2*4等于8，除4以为1*2*3等于6，题目已经提示我们了使用前缀和 后缀和。

解法一：暴力解法

暴力解法其实和我们上面举的例子一样，比如我们要求除第一个位置以外的值我们就从头遍历尾，要求第二个位置就从第一个开始遍历跳过我们自己然后依次遍历，以此类推。

但是时间复杂度太高了，O(N^2)

解法二：前缀积

本题的思路和上题的思路一样，但是有些细节有变化。

1.预处理前缀积以及后缀积

我们不需要i位置的元素，只要0~i-1位置的元素即可。表示如下：

f：表示前缀积：f [0,i -1 ] 区间内所有元素的乘积

我们要求i-1位置的乘积的时候我们知道i-2位置的乘积让它乘以i-1位置的值就可以了

f[i] = f [i-1] * nums[i-1]

注意：我们上面的f [i-1 ]位置是上图i-2的位置，因为我们f[i]表示的是i-1位置。

我们知道了i+2位置的乘积之后用它乘以i+1位置的值即可。

g：表示后缀积：g[i]表示：[i+1,n-1]

g[i] = g[i+1] * nums[i+1]

2.使用

我们在i这个位置填写数据的时候我们用f[i] * g[i]因为f[i]表示左边的乘积g表示右边的乘积

3.细节问题

当我们i等于0的时候，其实会越界访问所以我们需要处理，那么我们f(0)给什么值合适上面那道题我们给的是0，这道题我们不能给0因为0*nums[i-1]还是0，那么会影响我们的结果所以我们要给1,f(0) = 1，g(n-1) = 1

参考代码：

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int>f(n,1),g(n,1);vector<int> answer(n);//1.预处理前缀积 后缀积for(int i = 1;i<n;i++)f[i] = f[i-1] * nums[i-1];for(int i = n-2;i>=0;i--)g[i] = g[i+1] * nums[i+1];//2.使用for(int i = 0;i<n;i++){answer[i] = f[i] * g[i];}return answer;}
};

时间复杂度：O(N)

---

五、和为K的子数组

题目链接：560. 和为 K 的子数组 - 力扣（LeetCode）

题目描述：

前缀和+哈希表

以i位置为结尾的所有的子数组在[0,i-1]区间内，有多少个前缀和等于sum[i] - k就有多少个和为k的子数组，哈希表中分别存储前缀和、次数。

细节问题：

1.在计算i位置之前，哈希表里面只保存[0,i-1]位置的前缀和

2.不用真的创建一个前缀和数组，用一个变量sum来标记前一个位置的前缀和即可

3.如果整个前缀和等于k那么我们需要提前把hash[0] = 1。<0,1>

注意：不能使用滑动窗口来做优化(双指针)因为有0和负数，如下图这种情况我们left不断向右移动，那么有可能中间还有子数组和为 k

参考代码：

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int,int>hash;int sum = 0,ret = 0;hash[0] = 1;for(auto x : nums){sum += x;if(hash.count(sum - k)) ret += hash[sum - k];hash[sum]++;}return ret;}
};

时间复杂度为 O(n)，空间复杂度也为 O(n) 

---

六、和可被K整除的子数组

题目链接：和可被K整除的子数组

题目描述：

补充知识：

1.同余定理：

(a - b) / p = k.....0    => a % p = b % p

举个例子：(26-12) / 7   =>   26 % 7 = 12 % 7

7 % 2 = 1   -> 7 - 2 = 5 - 2 =3 -2 = 1

取余数的本质就是你这个数有多少个2的倍数就把2的倍数干掉，减到这个数比2小

(1+2 * 3) % 2 = 1(相当于有3个2的倍数，得出等式：(a + p * k) % p = a % p

证明：

(a- b) / p = k

a - b = p * k

a = b + p * k（左右相等，那么左右%p也相等）

a %p = (b + p * k) % p = b % p（p * k有k个p可以直接干掉）

2.C++，java：[负数 % 正数]的结果以及修正

负 % 正 = 负 修正 a % p + p 正负统一(a %p +p) % p（如果a为正数那么就多加了一个p所以再模一个p结果是不变的，如果是负数加上一个p刚好就是正确答案）

我们使用前缀和 + 哈希表

在[0,i-1]区间内，找到有多少个前缀和的余数等于(sun % k + k) % k，哈希表分别存储前缀和的余数、次数

大部分逻辑和上题差不多 

参考代码：

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int>hash;hash[0] = 1;//0这个数的余数int sum = 0,ret = 0;for(auto x : nums){sum += x;//算出当前位置的前缀和int r = (sum % k + k) % k;//修正后的余数if(hash.count(r)) ret +=hash[r%k];//统计结果hash[r]++;}return ret;}
};

时间复杂度为 O(n)，空间复杂度也为 O(n) 

---

七、连续数组

题目链接：连续数组

题目描述：

我们把问题转化一下：

1.将所有的0修改为-1

2.在数组中，找出最长的子数组，使子数组中所有的元素和为0

和为k的子数组 ->和为0的子数组

前缀和 + 哈希表

1.哈希表中分别存储前缀和、下标

2.使用完之后，丢进哈希表

3.如果有重复的<sum,i>只保留前面的那一对<sum,i>

4.默认的前缀和为0的情况hash[0] = -1，当我们的这段区间和为sum的时候我们要去0的前面也就是-1的位置找和为0的子区间(存的下标)

5.长度计算i - j + 1 - 1    =>  i - j

参考代码：

class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int,int> hash;hash[0] = -1; //默认有一个前缀和为0的情况int sum = 0,ret = 0;for(int i = 0 ; i<nums.size();i++){sum += nums[i] == 0 ? -1 : 1;if(hash.count(sum))  ret = max(ret,i - hash[sum]);else hash[sum] = i;}return ret;}
};

---

八、矩阵区域和

题目链接：矩阵区域和

题目描述：

题目要求：以5为中心分别像上左下右分别扩展k个单位，围城一个长方形的所有元素的和，这是假设k = 1，那么扩展一个单位。

假设求1这个位置，上左下右分别扩展1个单位，然后围成一个正方形，最后相加即可。1+2+4+5

求2这个位置，上左下右分别扩展1个单位然后围成正方形，相加即可，超出矩阵的范围不需要。1+2+3+4+5+6

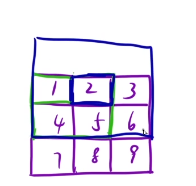
求5这个位置，上左下右分别扩展1个单位然后围成正方形，相加即可。1+2+3+4+5+6+7+8+9

解法：使用二维前缀和

dp[i][j] = dp[i-1][j]  + dp[i][j-1] -  dp[i-1][j-1] + mat[i][j]

因为多加了一个dp[i-1][j-1]所以再减去一个dp[i-1][j-1]。

如上就是初始化前缀和矩阵的递推公式，直接代入公式即可。

answer= dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]

这里加dp[x1-1][y1-1]是因为多减了一个dp[x1-1][y1-1]所以要加上

1.我们要求ans[i][j]位置

我们(i-k,j-k)用(x1,y2)表示

因为这个区间可能会越界，也就是说是(0,0)这个位置的时候我们不能越过，所以我们求一个最大值，如果小于0那么取最大值还是0如果大于0那么就是一个合法的区间。

x1 = max(0,i-k)

y1 = max(0,j-k)

我们(i+k,j+k)用(x2,y2)表示

我们的i+k,j+k可能会超过我们的(m-1,n-1)所以我们需要让它回到我们的m-1,n-1

x2 = min(m-1,i+k)

y2 = min(n-1,j+k) 

2.映射位置 

当我们dp数组要填1,1这个位置的值我们要去mat数组0,0这个位置找。dp(x,y)  -> mat(x-1,y-1)。

所以我们需要把dp[i][j] = dp[i-1][j]  + dp[i][j-1] -  dp[i-1][j-1] + mat[i][j]改为dp[i][j] = dp[i-1][j]  + dp[i][j-1] -  dp[i-1][j-1] + mat[i-1][j-1]

我们在填ans数据的时候使用dp数组需要+1因为ans(0,0)对应dp(1,1)位置。(x,y)  -> (x+1,y+1)。

这里有两种方式：

方法一：

answer[i][j] = dp[x2+1][y2+1] - dp[x1-1+1][y2+1]-dp[x2+1][y1-1+1] +dp [x1-1+1][y1-1+1];

方法二：我们在求下标那里进行+1即可，然后直接在dp数组拿值即可

x1 = max(0,i-k)+1

y1 = max(0,j-k)+1

x2 = min(m-1,i+k)+1

y2 = min(n-1,j+k) +1

参考代码：

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(),n = mat[0].size();//1.预处理前缀和矩阵vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i = 1;i <= m;i++)for(int j = 1;j<=n;j++)dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];//2.使用vector<vector<int>> answer(m,vector<int>(n));for(int i = 0;i < m;i++){for(int j = 0;j<n;j++){int x1 = max(0,i-k) + 1,y1 = max(0,j-k)+1;int x2 = min(m-1,i+k) + 1,y2 = min(n-1,j+k)+1;answer[i][j] = dp[x2][y2] - dp[x1-1][y2]-dp[x2][y1-1] +dp [x1-1][y1-1];}}return answer;}
};

---

总结

前缀和这个算法，重要思想就是预处理，当我们在解决一个问题的时候不太好解决的时候我们可以先预处理一下，预处理之后在解决效率是非常高的，直接解决时间复杂度是N^2级别，预处理一下直接变O(N)，这种就是典型的用空间换时间，因为我们多创建了一个数组，但是时间复杂度提高了一个级别。