分享半导体Fab 缺陷查看系统,平替klarity defect系统
分享半导体Fab 缺陷查看系统,平替klarity defect系统;开发了半年有余。
查看Defect Map,Defect image,分析Defect size,defect count trend.
不用再采用klarity defect系统(license 太贵)
也可以读取Klarf文件(中科飞测和KT的都可以识别)
技术要点:
首先认识Klarf中的三个值:
DiePitch:klarf recipe定义的Die Size ,X,Y,单位um。
DieOrigin:klarf中(0,0)Die左下角相对于klarf recipe坐标系中心的offset,X,Y,单位um。
SampleCenterLocation:wafer物理圆心相对于klarf recipe坐标系中心的offset,X,Y,单位um。
DB解读:
Klarity DB有自己的坐标系,依据这个坐标系来存klarf的值:
insp_wafer_summary中的CENTER_X,CENTER_Y:wafer圆心的在DB坐标系中的坐标值。
insp_wafer_summary中的ORIGIN_X,ORIGIN_Y:klarf recipe的坐标系中心在DB坐标系中的坐标值,klarf-SampleCenterLocation-X=
INSP_RECIPE中的ORIGIN_DIE_X,ORIGIN_DIE_Y:klarf(0,0)Die相对于klarf recipe的坐标系中心的矢量距离。
实现Defect Map、defect image查看


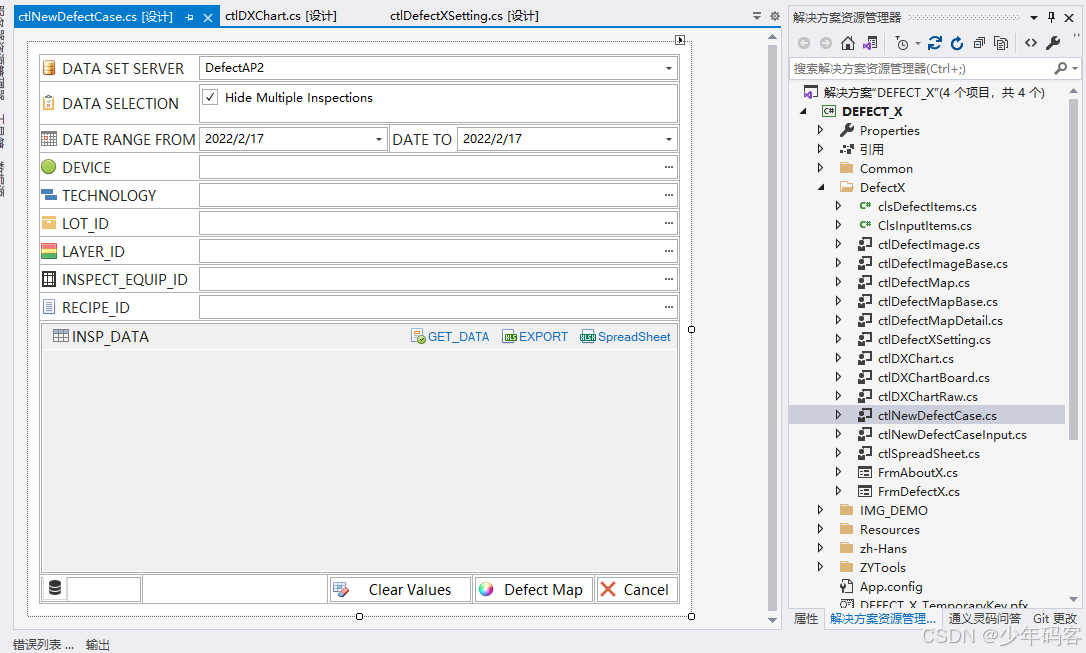
相关文章:

分享半导体Fab 缺陷查看系统,平替klarity defect系统
分享半导体Fab 缺陷查看系统,平替klarity defect系统;开发了半年有余。 查看Defect Map,Defect image,分析Defect size,defect count trend. 不用再采用klarity defect系统(license 太贵) 也可以…...
Java基础——分层解耦——IOC和DI入门
目录 三层架构 Controller Service Dao 编辑 调用过程 面向接口编程 分层解耦 耦合 内聚 软件设计原则 控制反转 依赖注入 Bean对象 如何将类产生的对象交给IOC容器管理? 容器怎样才能提供依赖的bean对象呢? 三层架构 Controller 控制…...
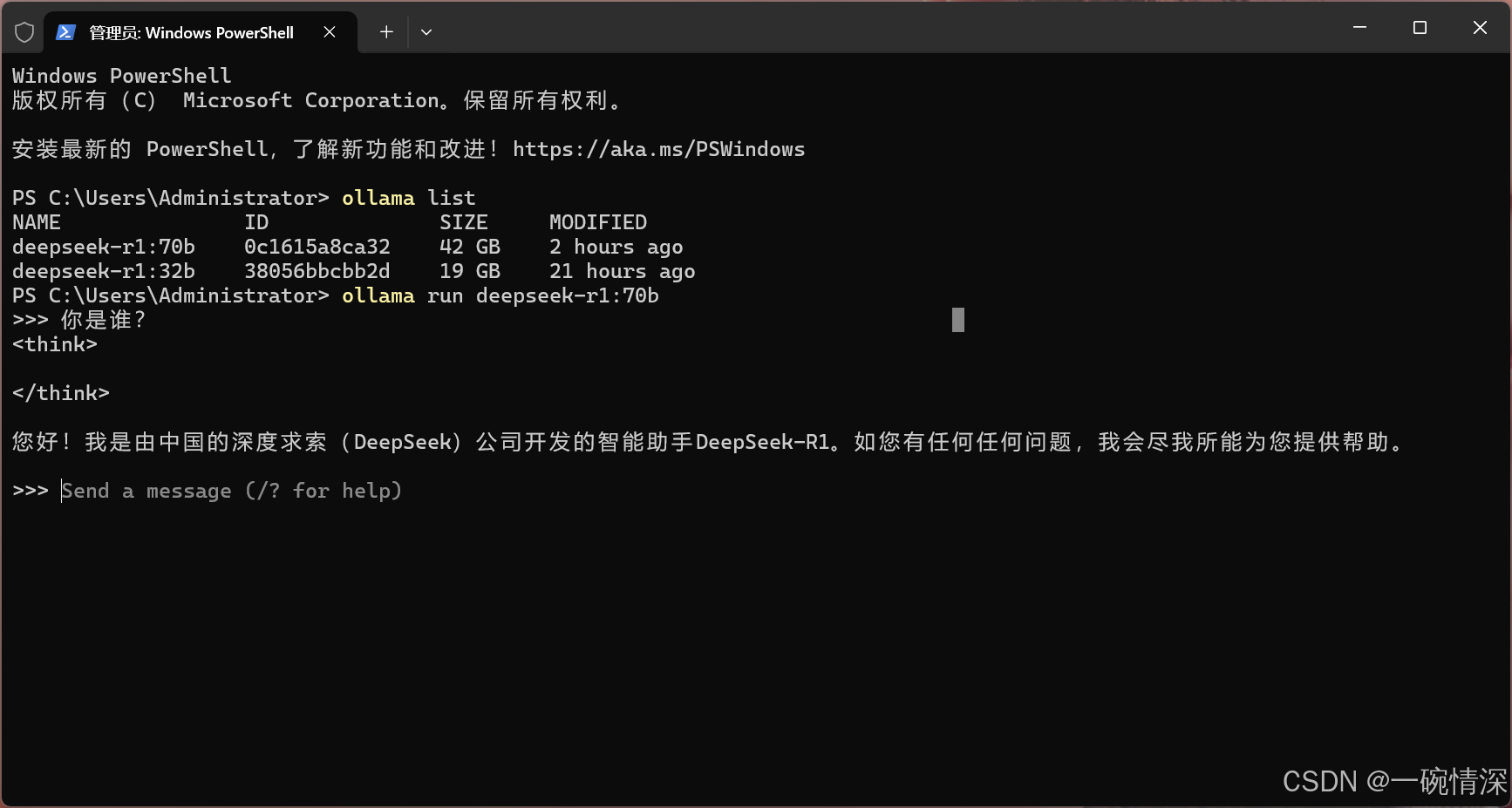
DeepSeek-R1 本地部署教程(超简版)
文章目录 一、DeepSeek相关网站二、DeepSeek-R1硬件要求三、本地部署DeepSeek-R11. 安装Ollama1.1 Windows1.2 Linux1.3 macOS 2. 下载和运行DeepSeek模型3. 列出本地已下载的模型 四、Ollama命令大全五、常见问题解决附:DeepSeek模型资源 一、DeepSeek相关网站 官…...
Vue3学习笔记-模板语法和属性绑定-2
一、文本插值 使用{ {val}}放入变量,在JS代码中可以设置变量的值 <template><p>{{msg}}</p> </template> <script> export default {data(){return {msg: 文本插值}} } </script> 文本值可以是字符串,可以是布尔…...

csapp笔记3.6节——控制(1)
本节解决了x86-64如何实现条件语句、循环语句和分支语句的问题 条件码 除了整数寄存器外,cpu还维护着一组单个位的条件码寄存器,用来描述最近的算数和逻辑运算的某些属性。可检测这些寄存器来执行条件分支指令。 CF(Carry Flag)…...

PYH与MAC的桥梁MII/MIIM
在学习车载互联网时,看到了一句话,Processor通过DMA直接存储访问与MAC之间进行数据的交互,MAC通过MII介质无关接口与PHY之间进行数据的交互。常见的以太网硬件结构是,将MAC集成进Processor芯片,将PHY留在Processor片外…...
)
国内flutter环境部署(记录篇)
设置系统环境变量 export PUB_HOSTED_URLhttps://pub.flutter-io.cn export FLUTTER_STORAGE_BASE_URLhttps://storage.flutter-io.cn使用以下命令下载flutter镜像 git clone -b stable https://mirror.ghproxy.com/https://github.com/<github仓库地址>#例如flutter仓…...

选择排序_75. 颜色分类
75. 颜色分类 - 力扣(LeetCode) 题目不追求稳定 可以选择选择排序 这是我没看教程代码之前写的 有点复杂了 我还把元素后移了 class Solution { public:void sortColors(vector<int>& nums) {int min_num_index -1;int min_num 3;for(int i…...

C++ Primer 标准库vector
欢迎阅读我的 【CPrimer】专栏 专栏简介:本专栏主要面向C初学者,解释C的一些基本概念和基础语言特性,涉及C标准库的用法,面向对象特性,泛型特性高级用法。通过使用标准库中定义的抽象设施,使你更加适应高级…...

C# 数组和列表的基本知识及 LINQ 查询
数组和列表的基本知识及 LINQ 查询 一、基本知识二、引用命名空间声明三、数组3.1、一维数组3.2、二维数组3.3、不规则数组 Jagged Array 四、列表 List4.1、一维列表4.2、二维列表 五、数组和列表使用 LINQ的操作和运算5.1、一维 LIST 删除所有含 double.NaN 的行5.2、一维 LI…...

大厂面试题备份20250201
20250201 面试策略 如果三面往后遇到传说中让人忍受不了的业余面试官,就舔着苟过去,入职大概率见不着他,但一二面遇到,反问环节就主动说不够match,让释放流程。 机器/深度学习 百面机器学习 5.4 通用CS 计算机网…...
w191教师工作量管理系统的设计与实现
🙊作者简介:多年一线开发工作经验,原创团队,分享技术代码帮助学生学习,独立完成自己的网站项目。 代码可以查看文章末尾⬇️联系方式获取,记得注明来意哦~🌹赠送计算机毕业设计600个选题excel文…...

Git 版本控制:基础介绍与常用操作
目录 Git 的基本概念 Git 安装与配置 Git 常用命令与操作 1. 初始化本地仓库 2. 版本控制工作流程 3. 分支管理 4. 解决冲突 5. 回退和撤销 6. 查看提交日志 前言 在软件开发过程中,开发者常常需要在现有程序的基础上进行修改和扩展。但如果不加以管理&am…...

讲清逻辑回归算法,剖析其作为广义线性模型的原因
1、逻辑回归算法介绍 逻辑回归(Logistic Regression)是一种广义线性回归分析模型。虽然名字里带有“回归”两字,但其实是分类模型,常用于二分类。既然逻辑回归模型是分类模型,为什么名字里会含有“回归”二字呢?这是因为其算法原…...

数据结构(1)——算法时间复杂度与空间复杂度
目录 前言 一、算法 1.1算法是什么? 1.2算法的特性 1.有穷性 2.确定性 3.可行性 4.输入 5.输出 二、算法效率 2.1衡量算法效率 1、事后统计方法 2、事前分析估计方法 2.2算法的复杂度 2.3时间复杂度 2.3.1定义 2.3.2大O渐进表示法 2.3.3常见时间复…...

K8s运维管理平台 - xkube体验:功能较多
目录 简介Lic安装1、需要手动安装MySQL,**建库**2、启动命令3、[ERROR] GetNodeMetric Fail:the server is currently unable to handle the request (get nodes.metrics.k8s.io qfusion-1) 使用总结优点优化 补充1:layui、layuimini和beego的详细介绍1.…...

spring源码阅读系列文章目录
对于spring认识首先要了解 spring相关概念术语,然后是如下的几句话牢记并反射出来: Bean怎么来的,通过BeanDefinitionBeanDefinition有Spring框架内置的,有手动定义或者自动配置扫描出来的(写个Demo工程)B…...

快速提升网站收录:利用网站新闻发布功能
本文转自:百万收录网 原文链接:https://www.baiwanshoulu.com/63.html 利用网站新闻发布功能快速提升网站收录是一个有效的策略。以下是一些具体的建议,帮助你更好地利用这一功能: 一、保持新闻更新频率 搜索引擎尤其重视网站的…...

【14】WLC3504 HA配置实例
1.概述 本文档使用 Cisco WLC 3504 实现无线控制器的高可用性。这里所指的HA是指WLC设备box-to-box的冗余。换句话说,即1:1的设备冗余,其中一个 WLC 将处于Active活动状态,而第二个 WLC 将处于Standby-hot热待机状态,通过RP冗余端口持续监控活动 WLC 的运行状况。两个 WLC…...

什么是LPU?会打破全球算力市场格局吗?
在生成式AI向垂直领域纵深发展的关键节点,一场静默的芯片革命正在改写算力规则。Groq研发的LPU(Language Processing Unit)凭借其颠覆性架构,不仅突破了传统GPU的性能天花板,更通过与DeepSeek等国产大模型的深度协同&a…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
