【数学】矩阵、向量(内含矩阵乘法C++)
目录
- 一、前置知识:向量(一列或一行的矩阵)、矩阵
- 1. 行向量
- 2. 列向量
- 3. 向量其余基本概念
- 4. 矩阵基本概念
- 5. 关于它们的细节
- 二、运算
- 1. 转置
- (1)定义
- (2)性质
- 2. 矩阵(向量)与矩阵(向量)的加减法
- 3. 点乘与乘法
- (1)定义:矩阵点乘
- (2)定义:向量点乘
- (3)定义:矩阵(向量)与标量的乘法
- (4)定义:矩阵(向量)与矩阵(向量)的乘法
- (5)性质:矩阵(向量)与矩阵(向量)的乘法
- (6)应用:矩阵快速幂,进行加速
- 三、拓展
- 1. 向量表示里的几何意义
- 2. 向量加法里的几何意义
- 3. 向量求反里的几何意义
- 四、结尾
一、前置知识:向量(一列或一行的矩阵)、矩阵
1. 行向量
例如 [ 1 1 4 ] \begin{bmatrix}1&1&4\end{bmatrix} [114],这就是一个行向量, [ 1 1 4 ] \begin{bmatrix}1&1&4\end{bmatrix} [114]可以理解为一个 1 1 1行 3 3 3列矩阵。
行向量: [ a 1 … a n ] \begin{bmatrix}a_1&\dots&a_n\end{bmatrix} [a1…an], n n n为任意取值。
2. 列向量
例如 [ 5 1 4 ] \begin{bmatrix}5\\1\\4\end{bmatrix} 514 ,这就是一个列向量, [ 5 1 4 ] \begin{bmatrix}5\\1\\4\end{bmatrix} 514 可以理解为一个 3 3 3行 1 1 1列的矩阵。
列向量: [ a 1 ⋮ a n ] \begin{bmatrix}a_1\\\vdots\\a_n\end{bmatrix} a1⋮an , n n n为任意取值。
3. 向量其余基本概念
向量是一个有方向与大小的量,它的起点可以是任意位置。
维度:
[ a 1 ] \begin{bmatrix}a_1\end{bmatrix} [a1],这是一个一维向量,它仅有一个数字。而 [ a 1 ⋮ a n ] \begin{bmatrix}a_1\\\vdots\\a_n\end{bmatrix} a1⋮an 与 [ a 1 … a n ] \begin{bmatrix}a_1&\dots&a_n\end{bmatrix} [a1…an],它们都是 n n n维的。
长度:
向量的长度也就是它的大小,我们称它为模。而模则为向量起点与终点之间的距离。
4. 矩阵基本概念
[ 1 1 4 1 6 1 4 1 5 ] \begin{bmatrix}1&1&4\\1&6&1\\4&1&5\end{bmatrix} 114161415 注: 这是一个维度为 3 × 3 3\times3 3×3的矩阵。
一个矩阵的维度表示为 m × n m\times n m×n,即 m m m行 n n n列的矩阵。
5. 关于它们的细节
向量可以视为一种特殊的矩阵,我们通常用大写字母表示矩阵;小写字母表示向量,可带一个小箭头,例如 v ⃗ \vec{v} v。例如 v i v_i vi表示向量 v v v的第 i i i项(即第 i i i个元素,行向量从左往右数,列向量从上往下), a i , j a_{i,j} ai,j或 A i , j A_{i,j} Ai,j表示矩阵 A A A的第 i i i行第 j j j列的元素。
二、运算
下文由于向量可以视为一种特殊的矩阵,且为了方便所以均用大写字母表示向量或矩阵。
1. 转置
(1)定义
A T A^T AT表示对 A A A进行转置,即 A A A的第 i i i行将变成
A T A^T AT的第 i i i列。若 A = [ 1 1 4 5 1 4 ] A=\begin{bmatrix}1&1&4\\5&1&4\end{bmatrix} A=[151144],则 A T = [ 1 5 1 1 4 4 ] A^T=\begin{bmatrix}1&5\\1&1\\4&4\end{bmatrix} AT= 114514 。
(2)性质
- ( A T ) T = A (A^T)^T=A (AT)T=A
- ( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT
2. 矩阵(向量)与矩阵(向量)的加减法
我们设 A ± B = C A\pm B=C A±B=C。
A ± B A\pm B A±B不是随便的, A A A与 B B B要求维度相同。且 C C C维度仍与 A A A、 B B B相同。
运算方式, C i , j = A i , j ± B i , j C_{i,j}=A_{i,j}\pm B_{i,j} Ci,j=Ai,j±Bi,j。
3. 点乘与乘法
(1)定义:矩阵点乘
我们设 A ∘ B = C A\circ B=C A∘B=C。
矩阵点乘的符号为“ ∘ \circ ∘”,其中 A A A、 B B B、 C C C均为矩阵,且维度相同。运算方法也很简单, C i , j = A i , j × B i , j C_{i,j}=A_{i,j}\times B_{i,j} Ci,j=Ai,j×Bi,j。
(2)定义:向量点乘
我们再设 A ⋅ B = n A\cdot B=n A⋅B=n。
显然 A A A、 B B B均为向量,且维度相同,而 n n n又是一个标量。那 n n n为多少? n = ∑ i = 1 m A i , j B i , j n=\sum_{i=1}^mA_{i,j}B_{i,j} n=∑i=1mAi,jBi,j( m m m为 A A A、 B B B的维度)。
(3)定义:矩阵(向量)与标量的乘法
我们再设 n A = B nA=B nA=B。
则 A A A、 B B B为矩阵(向量), n n n为标量,显而易见 B i , j = n A i , j B_{i,j}=nA_{i,j} Bi,j=nAi,j。
(4)定义:矩阵(向量)与矩阵(向量)的乘法
我们再再设 A B = C AB=C AB=C,设 A A A维度为 m × n m\times n m×n,而 B B B维度为 n × p n\times p n×p,则 C C C维度为 m × p m\times p m×p。
运算方式大概如此(复杂): C i , j = A i 行 ⋅ B j 列 C_{i,j}=A_{i行}\cdot B_{j列} Ci,j=Ai行⋅Bj列,即 C i , j = ∑ i = 1 n A i , k B k , j C_{i,j}=\sum_{i=1}^nA_{i,k}B_{k,j} Ci,j=∑i=1nAi,kBk,j。
(5)性质:矩阵(向量)与矩阵(向量)的乘法
- 没有交换律。
- 有结合律和分配率。
(6)应用:矩阵快速幂,进行加速
现在目光转置P1962,要运用矩阵乘法来解决求斐波那契数列第 n n n项(对 1 0 9 + 7 10^9+7 109+7取模)。
我们构造一个矩阵 A A A与矩阵 B B B, A = [ x y ] A=\begin{bmatrix}x&y\end{bmatrix} A=[xy], B = [ 1 1 1 0 ] B=\begin{bmatrix}1&1\\1&0\end{bmatrix} B=[1110],而 A B = [ x + y x ] AB=\begin{bmatrix}x+y&x\end{bmatrix} AB=[x+yx]。现在设 x x x是斐波那契数列的第 ( i + 1 ) (i+1) (i+1)项(简记 F i + 1 F_{i+1} Fi+1), y y y则为第 i i i项(简记 F i F_i Fi)。再把目光转回矩阵, A = [ F i + 1 F i ] A=\begin{bmatrix}F_{i+1}&F_i\end{bmatrix} A=[Fi+1Fi],
则 A B = [ F i + 1 + F n F i + 1 ] AB=\begin{bmatrix}F_{i+1}+F_n&F_{i+1}\end{bmatrix} AB=[Fi+1+FnFi+1],根据斐波那契数列的规律, F i + 1 + F i = F i + 2 F_{i+1}+F_i=F_{i+2} Fi+1+Fi=Fi+2,so A B = [ F i + 2 F i + 1 ] AB=\begin{bmatrix}F_{i+2}&F_{i+1}\end{bmatrix} AB=[Fi+2Fi+1],很容易发现 A B AB AB比 A A A中每项都进了一位,也就是说只要一直乘 B B B直至结果矩阵为 [ F n F n − 1 ] \begin{bmatrix}F_n&F_{n-1}\end{bmatrix} [FnFn−1],第一项就是P1962的答案。
但是直接递推到 F n F_n Fn是 O ( n ) O(n) O(n)的,乘到 F n F_n Fn也是 O ( n ) O(n) O(n)的。但是多个相同数相乘是数的幂,多个相同矩阵相乘是矩阵的幂,同样也可以使用快速幂,现在复杂度大约为 O ( k l o g 2 n ) O(klog_2n) O(klog2n)(有些小细节没有提及), k k k为矩阵乘法运算时耗掉的。这时当 n n n的值到达一个程度,时间就会大幅减少。
代码如下。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll p=1e9+7;
struct mat{ll nr,nc;ll m[15][15];mat(ll NR=0,ll NC=0){nr=NR,nc=NC;memset(m,0,sizeof(m));}mat operator=(mat b){nr=b.nr;nc=b.nc;for(int i=1;i<=nr;i++)for(int j=1;j<=nc;j++)m[i][j]=b.m[i][j];}
};
mat operator*(mat a,mat b){mat c(a.nr,b.nc);for(int i=1;i<=a.nr;i++){for(int j=1;j<=b.nc;j++){for(int k=1;k<=a.nc;k++){c.m[i][j]=(a.m[i][k]*b.m[k][j]%p+c.m[i][j])%p;}}}return c;
}
mat fastpow(mat a,ll b){if(b==1)return a;if(b%2==0)return fastpow(a*a,b/2);else return fastpow(a*a,b/2)*a;
}
int main(){ll n;cin>>n;if(n<=2){cout<<1;return 0;}mat fib(1,2),tmp(2,2),tmp2;fib.m[1][1]=1,fib.m[1][2]=1;tmp.m[1][1]=1,tmp.m[1][2]=1;tmp.m[2][1]=1;tmp2=fib*fastpow(tmp,n-2);cout<<tmp2.m[1][1];
}
三、拓展
1. 向量表示里的几何意义
例如有一个二维向量, v ⃗ = [ x y ] \vec{v}=\begin{bmatrix}x\\y\end{bmatrix} v=[xy],它将原点 ( 0 , 0 ) (0,0) (0,0)作为起点时,它的终点就是 ( x , y ) (x,y) (x,y)。
2. 向量加法里的几何意义

如图,向量 a a a与向量 b b b头尾相接最终与向量 c c c到达同一目的地,而恰好 a ⃗ + b ⃗ = c ⃗ \vec{a}+\vec{b}=\vec{c} a+b=c。
3. 向量求反里的几何意义
a ⃗ \vec{a} a与 − a ⃗ -\vec{a} −a的区别在于将 a ⃗ \vec{a} a旋转 180 ° 180\degree 180°就可以得 − a ⃗ -\vec{a} −a,即方向相反。
四、结尾

相关文章:

【数学】矩阵、向量(内含矩阵乘法C++)
目录 一、前置知识:向量(一列或一行的矩阵)、矩阵1. 行向量2. 列向量3. 向量其余基本概念4. 矩阵基本概念5. 关于它们的细节 二、运算1. 转置(1)定义(2)性质 2. 矩阵(向量࿰…...

设置git区分大小写
设置git区分大小写 1.全局设置 (影响全部仓库): git config --global core.ignorecase false2.仓库级别设置 (影响当前仓库): git config core.ignorecase false3.已经提交了大小写不一致的文件处理: git mv -f OldName newName # 强制重命名 git commit -m "Fix cas…...

排序算法与查找算法
1.十大经典排序算法 我们希望数据以一种有序的形式组织起来,无序的数据我们要尽量将其变得有序 一般说来有10种比较经典的排序算法 简单记忆为Miss D----D小姐 时间复杂度 :红色<绿色<蓝色 空间复杂度:圆越大越占空间 稳定性&…...

Github 2025-01-31Java开源项目日报 Top10
根据Github Trendings的统计,今日(2025-01-31统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Java项目10C项目1Kotlin项目1Bazel:快速、可扩展的多语言构建系统 创建周期:3564 天开发语言:Java协议类型:Apache License 2.0Star数量:2…...

Java进阶笔记(中级)
-----接Java进阶笔记(初级)----- 目录 集合多线程 集合 ArrayList 可以通过List来接收ArrayList对象(因为ArrayList实现了List接口) 方法:接口名 柄名 new 实现了接口的类(); PS: List list new ArrayList();遍历…...

2025游戏行业的趋势预测
一、市场现状 从总产值的角度来看,游戏总产值的增长率已经放缓,由增量市场转化为存量市场,整体的竞争强度将会加大,技术水平不强(开发技术弱、产品品质低、开发效率低)的公司将会面临更大的生存的困难。 从…...

4-ET框架demo的运行
开始操作 开始运行报错 编译Unity项目 状态同步demo运行 1-设置构建参数 CodeMode:ClientServer EPlayMode:EditorSimulateMode 点击ReGeneratoePerojectFiles调整代码结构 2-编译 在Unity.sln下编译项目 3-运行 以帧同步模式运行 1-合端运行 1.1 修改帧同步标记 …...

kamailio源文件modules.lst的内容解释
在执行make cfg 后,在kamailio/src目录下有一个文件modules.lst,内容如下: # this file is autogenerated by make modules-cfg# the list of sub-directories with modules modules_dirs:modules# the list of module groups to compile cf…...

亚远景-从SPICE到ASPICE:汽车软件开发的标准化演进
一、SPICE标准的起源与背景 SPICE,全称“Software Process Improvement and Capability dEtermination”,即“软件流程改进和能力测定”,是由国际标准化组织ISO、国际电工委员会IEC、信息技术委员会JTC1联合发起制定的ISO 15504标准。该标准旨…...

vue3 + ElementPlus 封装列表表格组件包含分页
在前端开发中,封装组件是必不可少的。今天就来封装一个通用的列表表格组件,包含分页功能,可以提高代码的复用性和可维护性。 1. 组件设计 Props: tableData:表格数据。columns:表格列配置。totalÿ…...

挑战项目 --- 微服务编程测评系统(在线OJ系统)
一、前言 1.为什么要做项目 面试官要问项目,考察你到底是理论派还是实战派? 1.希望从你的项目中看到你的真实能力和对知识的灵活运用。 2.展示你在面对问题和需求时的思考方式及解决问题的能力。 3.面试官会就你项目提出一些问题,或扩展需求…...

Med-R2:基于循证医学的检索推理框架:提升大语言模型医疗问答能力的新方法
Med-R2 : Crafting Trustworthy LLM Physicians through Retrieval and Reasoning of Evidence-Based Medicine Med-R2框架Why - 这个研究要解决什么现实问题What - 核心发现或论点是什么How - 1. 前人研究的局限性How - 2. 你的创新方法/视角How - 3. 关键数据支持How - 4. 可…...
具体踩坑记录(一))
Oh3.2项目升级到Oh5.0(鸿蒙Next)具体踩坑记录(一)
目录 1.自动修复部分 Cause: The project structure and configuration require an upgrade. Solution: 1. Use Migrate Assistant to auto-upgrade the project structure and configuration. 2. Manually upgrade the project structure and configuration by following th…...
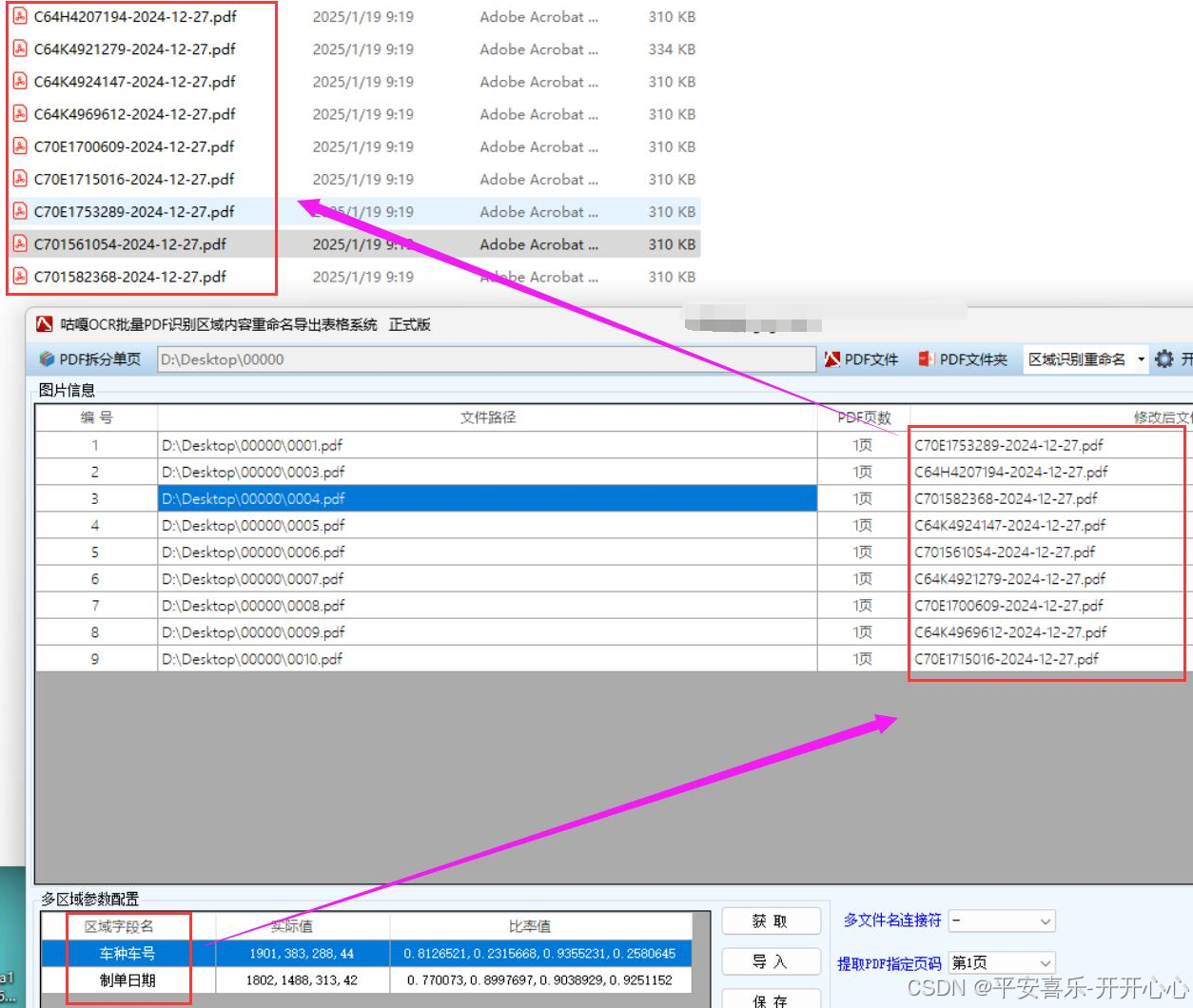
【自动化办公】批量图片PDF自定义指定多个区域识别重命名,批量识别铁路货物运单区域内容改名,基于WPF和飞桨ocr深度学习模型的解决方案
项目背景介绍 铁路货运企业需要对物流单进行长期存档,以便后续查询和审计。不同的物流单可能包含不同的关键信息,通过自定义指定多个区域进行识别重命名,可以使存档的图片文件名具有统一的规范和明确的含义。比如,将包含货物运单…...

Spring Boot篇
为什么要用Spring Boot Spring Boot 优点非常多,如: 独立运行 Spring Boot 而且内嵌了各种 servlet 容器,Tomcat、Jetty 等,现在不再需要打成 war 包部署到 容器 中,Spring Boot 只要打成一个可执行的 jar 包就能独…...
)
Unity3D学习笔记(二)
一、Unity编辑器相关 1、 Unity特殊的专属文件夹 1) Editor:编辑器相关资源可以放到此文件中,包括图片、脚本等文件。 2)Editor Default Resources:配合Editor使用不会打包到包中 3)Plugins:存放第三方SD…...

个人毕业设计--基于HarmonyOS的旅行助手APP的设计与实现(挖坑)
在行业混了短短几年,却总感觉越混越迷茫,趁着还有心情学习,把当初API9 的毕业设计项目改成API13的项目。先占个坑,把当初毕业设计的文案搬过来 摘要:HarmonyOS(鸿蒙系统)是华为公司推出的面向全…...

游戏引擎 Unity - Unity 打开项目、Unity Editor 添加简体中文语言包模块、Unity 项目设置为简体中文
Unity Unity 首次发布于 2005 年,属于 Unity Technologies Unity 使用的开发技术有:C# Unity 的适用平台:PC、主机、移动设备、VR / AR、Web 等 Unity 的适用领域:开发中等画质中小型项目 Unity 适合初学者或需要快速上手的开…...

python开发:爬虫示例——GET和POST请求处理
一、Get请求 import json import requests#输入示例:urlhttps://www.baidu.com #RequestHeader:F12标头-请求标头-原始-复制到这(忽略第一句) def GetRequest(url,RequestHeader""):try:dic{}RequestHeaderList RequestHeader.s…...

开源数据分析工具 RapidMiner
RapidMiner是一款功能强大且广泛应用的数据分析工具,其核心功能和特点使其成为数据科学家、商业分析师和预测建模人员的首选工具。以下是对RapidMiner的深度介绍: 1. 概述 RapidMiner是一款开源且全面的端到端数据科学平台,支持从数据准备、…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...
