ABC 289 G - Shopping in AtCoder store 数学推导+凸包
大意:
n个顾客,每个人有一个购买的欲望bi,m件物品,每一件物品有一个价值ci,每一个顾客会买商品当且仅当bi+ci>=定价.
现在要求对每一个商品定价,求出它的最大销售值(数量*定价)
n,m<=2e5
思路:
首先m件物品都是相互独立的,可以看成m个询问
另外,不妨对n个人的购买力做一个降序排序,显然它们满足单调性
不难发现,一旦我们定下了物品的价格,那么最终的销售额就由销售数量决定,也就是会有多少人买。此时在销售数量减少的情况下,我们一定会尽可能地抬高价格。从而我们得到一个结论:每一个商品i的定价一定是bj+ci(1<=j<=n).这是因为,它刚好可以使某个人会买这件商品。假设最优定价不满足这个结论,显然我们可以直接抬高它使其达到另一个bj+ci,此时我们在购买人数不变的情况下就提高了单价,这是更优的。
现在商品单价就只有n个选择了,对于商品i,我们的销售额就是max{j*(bj+ci)}(1<=j<=n),因为我们是按购买力降序排序,如果第j个人刚好买的起,那么前面的人一定都买的起(这里也不用关心购买力重复的问题,因为重复的话,后面相同购买力的的人对应的决策一定会更好)。
此时我们就转化了题意:对于一个i(1<=i<=m),找到max{j*(bj+ci)}
这里借一下官方题解的图片:
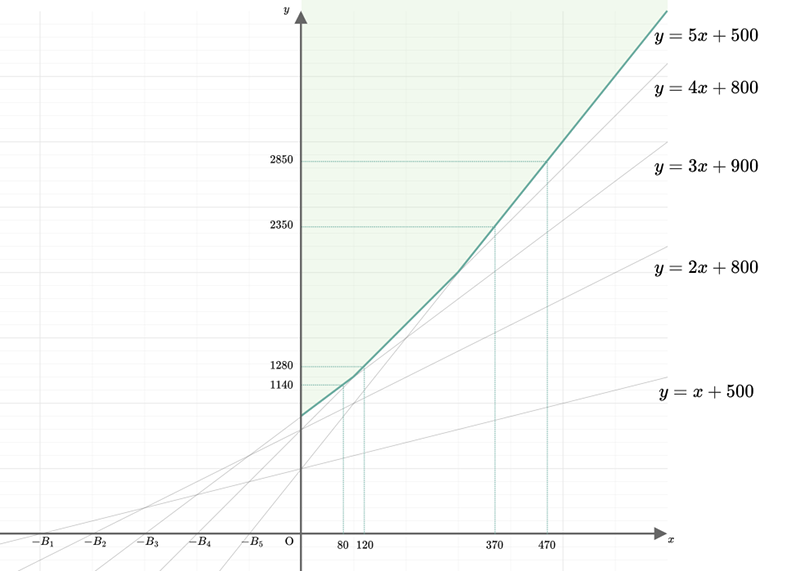
我们令横坐标为ci,纵坐标为对应的价值,不同j的选择对应不同的总价值。显然我们最后是要找一个凸包,最后的答案就是横坐标对应的凸包上的点的纵坐标了
求凸包的话,我们从1-n开始遍历的话,直线的斜率是单调递增的,
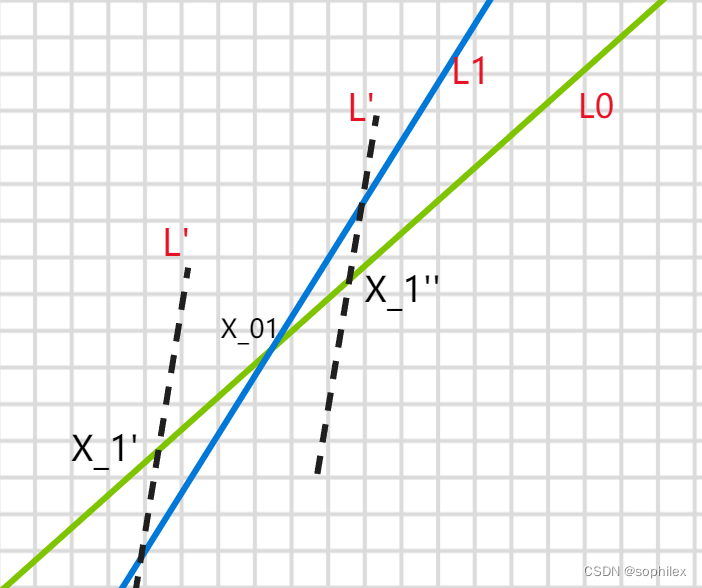
不妨用单调栈来更新当前段的最大值对应的直线
假设当前栈内有两条直线L0,L1,交点为X_01,那么对于新加入的直线L',如果它与L0的交点X_1'的横坐标小于X_01的横坐标,显然就可以把L1淘汰掉了,因为它后面也不会有比L‘更大的机会了。
关于这个判断,就只要计算一下交点横坐标就可以了。
最后我们得到了一个凸包,那么对于一个ci,我们去二分找到它在那一段线段上就可以了
时间复杂度O(n+mlogn)
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define mk make_pair
const ll N=2e5+10;
ll n,m;
ll b[N];
ll c[N];
struct P
{double x,y;
};
vector<pair<double,P>> vt;
double cross(P p1,P p2,P p3) {return (p2.x-p1.x)*(p3.y-p1.y)-(p3.x-p1.x)*(p2.y-p1.y);
}
bool judge(ll x,ll tar)
{return vt[x].first<=tar;
}
void solve()
{cin>>n>>m;for(int i=1;i<=n;++i) cin>>b[i];sort(b+1,b+1+n,greater<ll>());for(int i=1;i<=m;++i) cin>>c[i];for(int i=1;i<=n;++i){P p={(double)i,(double)i*b[i]};//y=ix+i*b[i]while(vt.size()>=2&&cross(p,vt.rbegin()->second,(next(vt.rbegin()))->second)<0) vt.pop_back();//弹出无用的直线double x=0;if(vt.size()){P pp=vt.back().second;x=(pp.y-p.y)/(p.x-pp.x);} vt.push_back(make_pair(x,p));} ll len=vt.size();
// for(auto i:vt)
// {
// cout<<i.second.x<<" "<<i.second.y<<endl;
// }for(int i=1;i<=m;++i){ll l=0,r=len-1;while(l<=r){ll mid=l+r>>1;if(judge(mid,c[i])) l=mid+1;else r=mid-1;}P op=vt[l-1].second;cout<<(ll)(op.x*c[i]+op.y)<<" ";}
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
// ll t;cin>>t;while(t--)solve();return 0;
}相关文章:

ABC 289 G - Shopping in AtCoder store 数学推导+凸包
大意: n个顾客,每个人有一个购买的欲望bi,m件物品,每一件物品有一个价值ci,每一个顾客会买商品当且仅当bici>定价. 现在要求对每一个商品定价,求出它的最大销售值(数量*定价) n,m<2e5 思路&#x…...

ARM Linux 如何在sysfs用户态命令行中控制 GPIO 引脚?
ARM Linux 如何在sysfs用户态命令行中控制 GPIO 引脚?我们在开发工作中,经常需要确定内核gpio驱动,是否有异常,或者在没有应用的情况下,像控制某个外设,这时我们就可以在控制台命令行中,用命令导…...
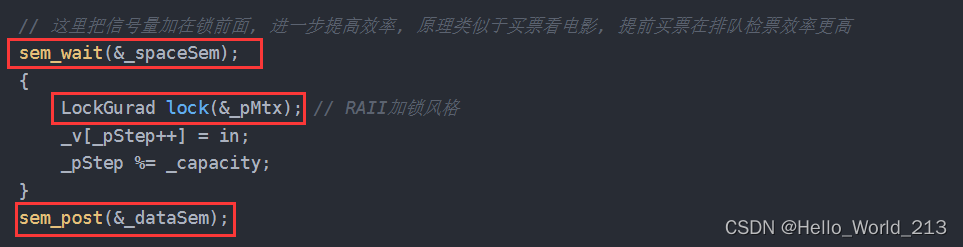
【Linux】生产者消费者模型 - 详解
目录 一.生产者消费者模型概念 1.为何要使用生产者消费者模型 2.生产者消费者之间的关系 3.生产者消费者模型的优点 二.基于阻塞队列的生产消费模型 1.在阻塞队列中的三种关系 2.BlockingQueue.hpp - 阻塞队列类 3.LockGurad.hpp - RAII互斥锁类 4.Task.hpp - 在阻塞队…...

源码深度解析Spring Bean的加载
在应用spring 的过程中,就会涉及到bean的加载,bean的加载经历一个相当复杂的过程,bean的加载入口如下: 使用getBean()方法进行加载Bean,最终调用的是AbstractBeanFactory.doGetBean() 进行Bean的…...
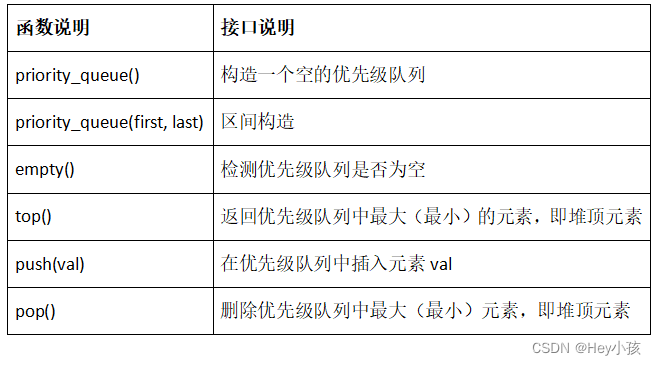
STL——priority_queue
一、priority_queue介绍及使用 1.priority_queue文档介绍 (1)优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。 (2)此上下文类似与堆,在堆中可以…...
Springboot集成工作流Activity
介绍 官网:https://www.activiti.org/ 一 、工作流介绍 1.工作流(workflow) 就是通过计算机对业务流程自动化执行管理,它主要解决的是“使在多个参与这之间按照某种预定义规则自动化进行传递文档、信息或任务的过程,…...

2023软件测试工程师涨薪攻略,3年如何达到月薪30K?
1.软件测试如何实现涨薪 首先涨薪并不是从8000涨到9000这种涨薪,而是从8000涨到15K加到25K的涨薪。基本上三年之内就可以实现。 如果我们只是普通的有应届毕业生或者是普通本科那我们就只能从小公司开始慢慢往上走。 有些同学想去做测试,是希望能够日…...
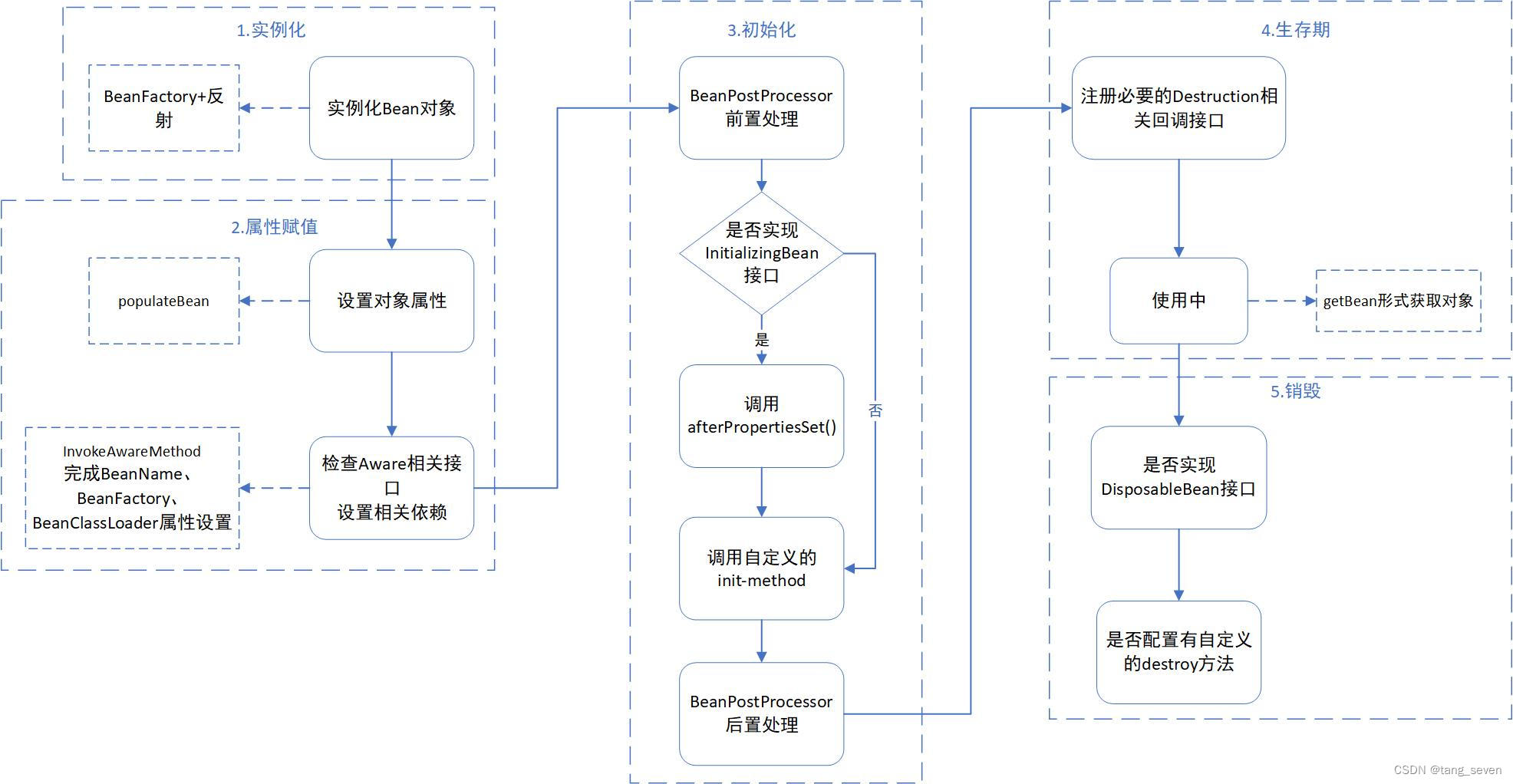
Java面试——Spring Bean相关知识
目录 1.Bean的定义 2.Bean的生命周期 3.BeanFactory及Factory Bean 4.Bean的作用域 5.Bean的线程安全问题 1.Bean的定义 JavaBean是描述Java的软件组件模型。在Java模型中,通过JavaBean可以无限扩充Java程序的功能,通过JavaBean的组合可以快速的生…...

上班在群里摸鱼,逮到一个字节8年测试开发,聊过之后羞愧难当...
老话说的好,这人呐,一旦在某个领域鲜有敌手了,就会闲得某疼。前几天我在上班摸鱼刷群的时候认识了一位字节测试开发大佬,在字节工作了8年,因为本人天赋比较高,平时工作也兢兢业业,现在企业内有一…...
HTTP、WebSocket和Socket.IO
一、HTTP协议 HTTP协议是Hyper Text Transfer Protocol(超文本传输协议)。HTTP 协议和 TCP/IP 协议族内的其他众多的协议相同, 用于客户端和服务器之间的通信。请求访问文本或图像等资源的一端称为客户端, 而提供资源响应的一端称…...

Fluent Python 笔记 第 11 章 接口:从协议到抽象基类
本章讨论的话题是接口:从鸭子类型的代表特征动态协议,到使接口更明确、能验证实现是否符合规定的抽象基类(Abstract Base Class,ABC)。 11.1 Python 文化中的接口和协议 对 Python 程序员来说,“X 类对象”“X 协 议”和“X 接口”都是一个…...

【Spark分布式内存计算框架——Spark Core】11. Spark 内核调度(下)
8.5 Spark 基本概念 Spark Application运行时,涵盖很多概念,主要如下表格: 官方文档:http://spark.apache.org/docs/2.4.5/cluster-overview.html#glossary Application:指的是用户编写的Spark应用程序/代码&#x…...

Java中的函数
1.String.trim() : 主要有2个用法: 1、就是去掉字符串中前后的空白;这个方法的主要可以使用在判断用户输入的密码之类的。 2、它不仅可以去除空白,还可以去除字符串中的制表符,如 ‘\t’,\n等。 2.Integer.parseInt() : 字符串…...

实验6-霍纳法则及变治技术
目录 1.霍纳法则(Horners rule) 2.堆排序 3.求a的n次幂 1.霍纳法则(Horners rule) 【问题描述】用霍纳法则求一个多项式在一个给定点的值 【输入形式】输入三行,第一行是一个整数n,表示的是多项式的最高次数;第二行多项式的系数组P[0...n](从低到高存储);第三行是…...
IP地址:揭晓安欣警官自证清白的黑科技
《狂飙》这部电视剧,此从播出以来可谓是火爆了,想必大家都是看过的。剧中,主人公“安欣”是一名警察。一直在与犯罪分子做斗争。 莽村的李顺案中,有匿名者这个案件在网上发帖恶意造谣,说安欣是黑恶势力的保护伞&#…...
考研复试机试 | C++
目录1.盛水最多的容器<11>题目代码:2.整数转罗马数字题目:代码:3. 清华大学机试题 abc题目题解4.清华大学机试题 反序数题目描述代码对称平方数题目代码:5. 杭电上机题 叠筐题目:代码pass:关于清华大…...
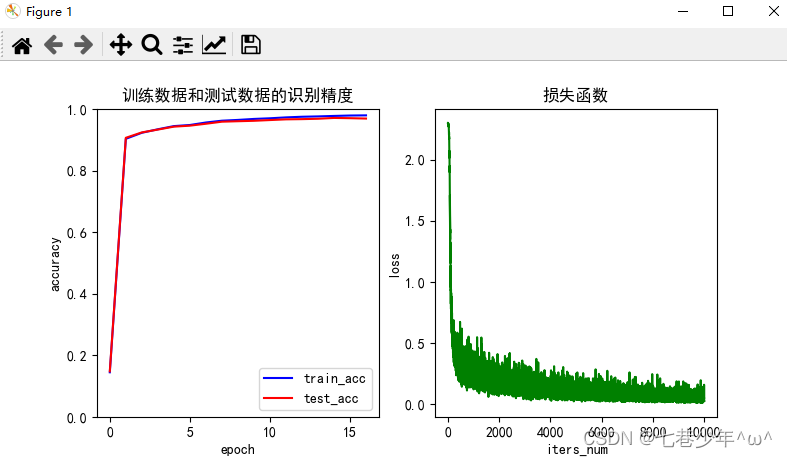
第四章.误差反向传播法—误差反向传播法实现手写数字识别神经网络
第四章.误差反向传播法 4.3 误差反向传播法实现手写数字识别神经网络 通过像组装乐高积木一样组装第四章中实现的层,来构建神经网络。 1.神经网络学习全貌图 1).前提: 神经网络存在合适的权重和偏置,调整权重和偏置以便拟合训练数据的过程称…...

IB学习者的培养目标有哪些?
IB课程强调要培养年轻人的探究精神,在富有渊博知识的同时,更要勤于思考,敢于思考,尊重和理解跨文化的差异,坚持原则维护公平,让这个世界充满爱与和平,让这个世界变得更加美好。上一次我们为大家…...
C++类基础(十三)
类的继承 ● 通过类的继承(派生)来引入“是一个”的关系( 17.2 — Basic inheritance in C) – 通常采用 public 继承( struct V.S. class ) – 注意:继承部分不是类的声明 – 使用基类的指针…...
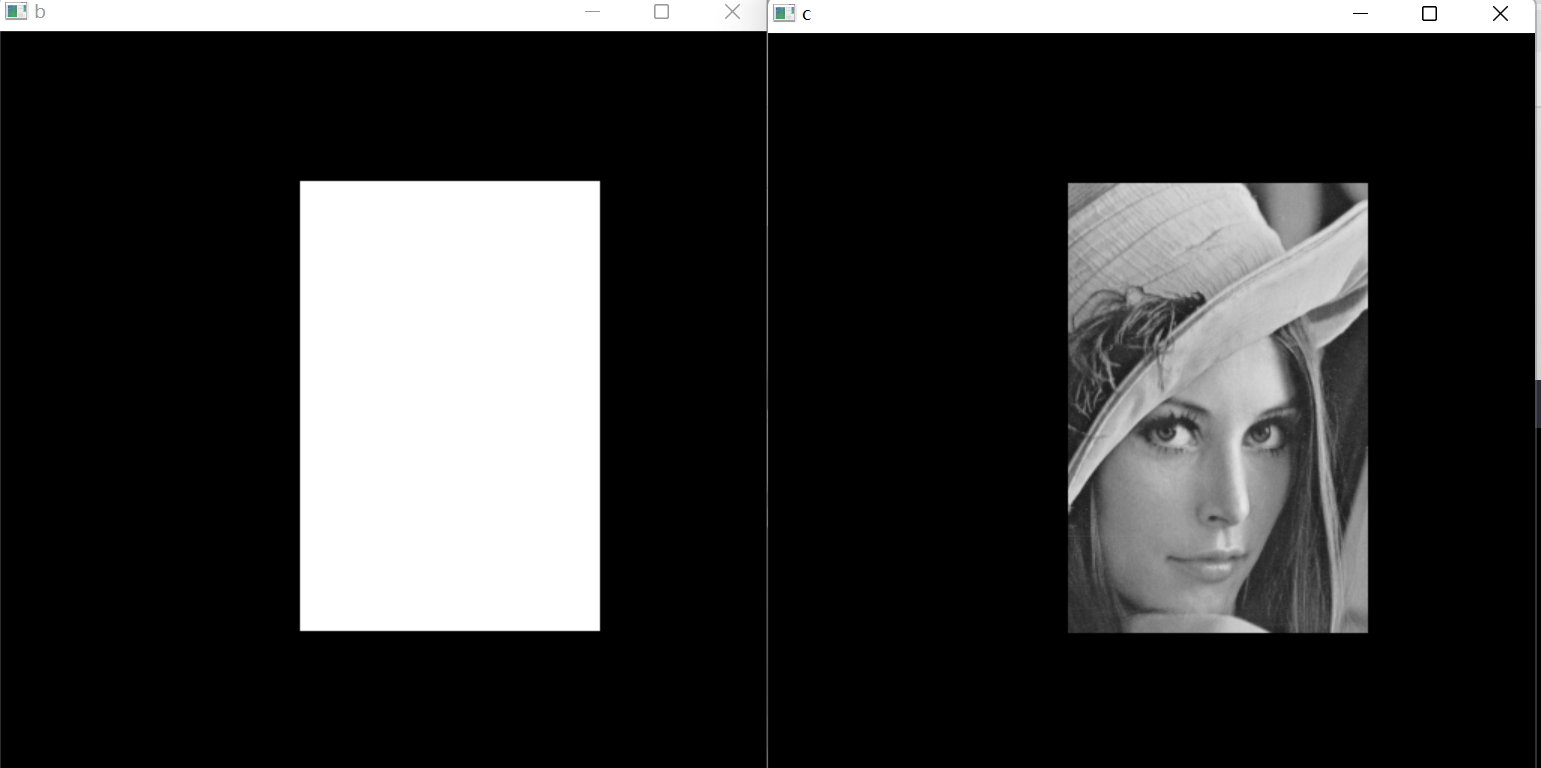
03 OpenCV图像运算
文章目录1 普通加法1 加号相加2 add函数2 加权相加3 按位运算1 按位与运算2 按位或运算、非运算4 掩膜1 普通加法 1 加号相加 在 OpenCV 中,图像加法可以使用加号运算符()来实现。例如,如果要将两幅图像相加,可以使用…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...
