深入剖析B树、B+树与B*树:从二叉树到多叉树的演进
引言
在计算机科学中,树结构是数据存储和检索的核心工具之一。从二叉树到二叉排序树,再到平衡二叉树,我们已经看到了这些数据结构在高效处理数据方面的优势。然而,随着数据量的爆炸式增长,二叉树的局限性逐渐显现出来。面对海量数据,二叉树的深度可能变得过大,导致操作效率下降。为了解决这一问题,多叉树应运而生。本文将深入探讨多叉树中的几种重要变体——B树、B+树和B*树,分析它们的背景、应用场景及实际意义,帮助读者更好地理解这些数据结构。
主体部分
1. 二叉树的局限性
1.1 二叉树的问题
二叉树的操作效率虽然较高,但在处理海量数据时,存在以下问题:
-
树的高度过大:随着数据量的增加,二叉树的高度会迅速增长,导致查找、插入和删除操作的时间复杂度增加。
-
I/O操作频繁:在磁盘存储系统中,二叉树的深度过大意味着需要更多的磁盘I/O操作,这会显著降低数据检索的效率。
-
空间利用率低:二叉树的每个节点只能存储一个数据项,导致空间利用率较低,尤其是在处理大规模数据时。
1.2 多叉树的引入
为了克服二叉树的局限性,多叉树应运而生。多叉树允许每个节点拥有更多的数据项和子节点,从而减少树的高度,优化操作效率。通过重新组织节点,多叉树能够显著降低树的高度,减少I/O操作次数,提升数据检索的效率。
2. 2-3树:多叉树的起点
2.1 2-3树的特点
2-3树是最简单的B树,具有以下特点:
-
节点类型:2-3树的每个节点可以包含1个或2个数据项,并且有2个或3个子节点。
-
平衡性:2-3树始终保持平衡,所有叶子节点位于同一层。
-
插入规则:插入新数据时,若节点已满,则需要进行节点拆分,确保树的结构满足2-3树的条件。
2.2 2-3树的应用案例
以数列{16,24,12,32,14,26,34,10,8,28,38,20}为例,构建2-3树并保证数据插入的顺序。插入时若节点不满足条件,则需拆分节点,确保满足上述条件。
插入规则:
-
如果插入的节点未满,直接插入。
-
如果插入的节点已满,则拆分节点,并将中间值提升到父节点。
-
如果父节点也满了,继续拆分,直到根节点。
通过2-3树的构建过程,我们可以看到多叉树如何通过增加每个节点的数据项和子节点数量来减少树的高度,从而提升操作效率。
3. B树:多叉树的经典代表
3.1 B树的基本介绍
B树(B-tree)是一种平衡的多路搜索树,广泛应用于文件系统和数据库系统中。B树的特点包括:
-
多路分支:每个节点可以有多个子节点,通常远多于2个。
-
平衡性:B树始终保持平衡,所有叶子节点位于同一层。
-
高效检索:B树通过降低树的高度,减少I/O操作次数,显著提升了数据检索效率。
3.2 B树的应用场景
B树在数据库和文件系统中有着广泛的应用。
例如,在600亿个元素中,B树最多只需4次I/O操作即可读取目标元素。
这种高效的检索能力使得B树成为处理大规模数据的理想选择。
4. B+树:B树的优化版本
4.1 B+树的基本介绍
B+树是B树的变体,也是一种多路搜索树,具有以下特点:
-
叶子节点链表:B+树的所有数据项都存储在叶子节点中,并且叶子节点通过链表连接,便于范围查询和顺序访问。
-
非叶子节点只存储索引:B+树的非叶子节点只存储索引信息,不存储实际数据,这使得B+树在范围查询和顺序访问方面具有更高的效率。
4.2 B+树的应用场景
B+树更适合文件索引系统,因为其叶子节点链表结构便于范围查询和顺序访问。
例如,在数据库系统中,B+树常用于索引的存储,能够快速定位数据并进行范围查询。
5. B*树:B+树的进一步优化
5.1 B*树的基本介绍
B树是B+树的变体,在非根和非叶子节点增加了指向兄弟节点的指针。B树的特点包括:
-
兄弟节点指针:B*树通过增加兄弟节点指针,提高了节点的空间利用率。
-
更高的空间效率:B*树在空间利用率方面优于B+树,适用于对空间效率要求较高的场景。
5.2 B*树的应用场景
B树在空间利用率方面优于B+树,适用于对空间效率要求较高的场景。
例如,在内存受限的嵌入式系统中,B树可以更有效地利用存储空间。
结论
通过本文的深入剖析,我们了解到二叉树在处理海量数据时的局限性,以及多叉树(特别是B树、B+树和B*树)如何通过优化节点结构和减少树的高度来提升数据检索效率。这些树结构在文件系统和数据库系统中有着广泛的应用,理解它们的原理和应用场景对于计算机科学从业者至关重要。
希望本文能够帮助读者更好地理解B树、B+树和B*树,并在实际项目中灵活运用这些数据结构。如果你对这个系列的其他文章感兴趣,欢迎继续关注我的博客。
代码示例:
# 2-3树节点插入示例
class Node:def __init__(self, keys=None, children=None):self.keys = keys or []self.children = children or []def is_leaf(self):return len(self.children) == 0def __repr__(self):return f"Node(keys={self.keys}, children={self.children})"def insert(node, key):if not node.keys:node.keys.append(key)return nodeif node.is_leaf():node.keys.append(key)node.keys.sort()if len(node.keys) > 2:return split(node)return nodei = 0while i < len(node.keys) and key > node.keys[i]:i += 1child = insert(node.children[i], key)if len(child.keys) > 2:return split_child(node, i, child)return nodedef split(node):mid = len(node.keys) // 2left = Node(keys=node.keys[:mid])right = Node(keys=node.keys[mid+1:])return Node(keys=[node.keys[mid]], children=[left, right])def split_child(parent, i, child):mid = len(child.keys) // 2parent.keys.insert(i, child.keys[mid])parent.children[i] = Node(keys=child.keys[:mid])parent.children.insert(i+1, Node(keys=child.keys[mid+1:]))return parent# 示例使用
root = Node()
keys = [16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20]
for key in keys:root = insert(root, key)
print(root)系列文章
-
二叉树: 从基础到高级的应用和实现。
-
二叉排序树:如何利用二叉排序树实现高效的数据检索与动态更新。
-
平衡二叉树:如何通过平衡二叉树解决普通二叉树的性能问题。
-
顺序存储二叉树:数据结构的灵活转换与优化。
-
红黑树:红黑树的特性及其在Java集合框架中的应用。
-
其他树结构:B树、B+树、Trie树等多叉树的应用与实现。
如果你对平衡二叉树或其他树结构有任何疑问,欢迎在评论区留言讨论!
相关文章:

深入剖析B树、B+树与B*树:从二叉树到多叉树的演进
引言 在计算机科学中,树结构是数据存储和检索的核心工具之一。从二叉树到二叉排序树,再到平衡二叉树,我们已经看到了这些数据结构在高效处理数据方面的优势。然而,随着数据量的爆炸式增长,二叉树的局限性逐渐显现出来…...

《算法篇:三数之和问题的两种解法》
问题描述 给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a b c 0 ?找出所有满足条件且不重复的三元组。 注意:答案中不可以包含重复的三元组。 给定数组 nums [-1, 0,…...

【2025】基于springboot+uniapp的乡村旅游小程序系统统(源码、万字文档、图文修改、调试答疑)农家乐预约
乡村旅游小程序系统通过 Spring Boot 与 uniapp 技术栈的深度整合,为乡村旅游产业打造了一个功能全面、交互流畅、性能稳定的综合服务平台。系统根据不同角色(管理员、商家、用户)的业务需求,提供了针对性的功能模块,实…...

DeepSeek Kimi详细生成PPT的步骤
以下是使用 DeepSeek 和 Kimi 协作生成 PPT 的详细步骤,结合了两者的优势实现高效创作: 第一步:使用 DeepSeek 生成 PPT 大纲或内容 明确需求并输入提示词 在 DeepSeek 的对话界面中,输入具体指令,要求生成 PPT 大纲或…...

【Film】MM-StoryAgent:沉浸式叙事故事书视频生成,具有跨文本、图像和音频的多代理范式
MM-StoryAgent:沉浸式叙事故事书视频生成,具有跨文本、图像和音频的多代理范式 https://arxiv.org/abs/2503.05242 MM-StoryAgent: Immersive Narrated Storybook Video Generation with a Multi-Agent Paradigm across Text, Image and Audio The rapid advancement of larg…...

Tweak Power:全方位电脑系统优化的高效工具
在日常使用电脑时,系统性能的下降、垃圾文件的堆积以及硬盘的老化等问题常常困扰着用户。为了提升电脑性能、优化系统运行,许多人会选择系统优化工具。然而,国内一些系统优化软件常常因为广告过多或功能冗杂而让人望而却步。此时,…...

LVDS系列3:Xilinx的IOBUFDS原语
前面两节讲解了差分转单端的IBUFDS原语和单端转差分的OBUFDS原语,今天来讲一个同时带有两者功能的原语IOBUFDS; 前述的IBUFDS原语只能接收外部差分信号,此时连接管脚为input管脚,OBUFDS只能向外部输出差分信号,此时连接…...
Git和GitHub基础教学
文章目录 1. 前言2. 历史3. 下载安装Git3.1 下载Git3.2 安装Git3.3 验证安装是否成功 4. 配置Git5. Git基础使用5.1 通过Git Bash使用5.1.1 创建一个新的仓库。5.1.1.1 克隆别人的仓库5.1.1.2 自己创建一个本地仓库 5.1.2 管理存档 5.2 通过Visual Studio Code使用 6. Git完成远…...

Django-ORM-select_related
Django-ORM-select_related 作用使用场景示例无 select_related 的查询有 select_related 的查询 如何理解 "只发起一次查询,包含所有相关作者信息"1. select_related 的工作原理2. 具体示例解析3. 为什么只发起一次查询 数据库中的books量巨大࿰…...

蓝桥杯 k倍区间
题目描述 给定一个长度为 NN 的数列,A1,A2,⋯ANA1,A2,⋯AN,如果其中一段连续的子序列 Ai,Ai1,⋯AjAi,Ai1,⋯Aj ( i≤ji≤j ) 之和是 KK 的倍数,我们就称这个区间 [i,j][i,j] 是 K 倍区间。 你能求出数列中总共有多少个 KK 倍区间…...
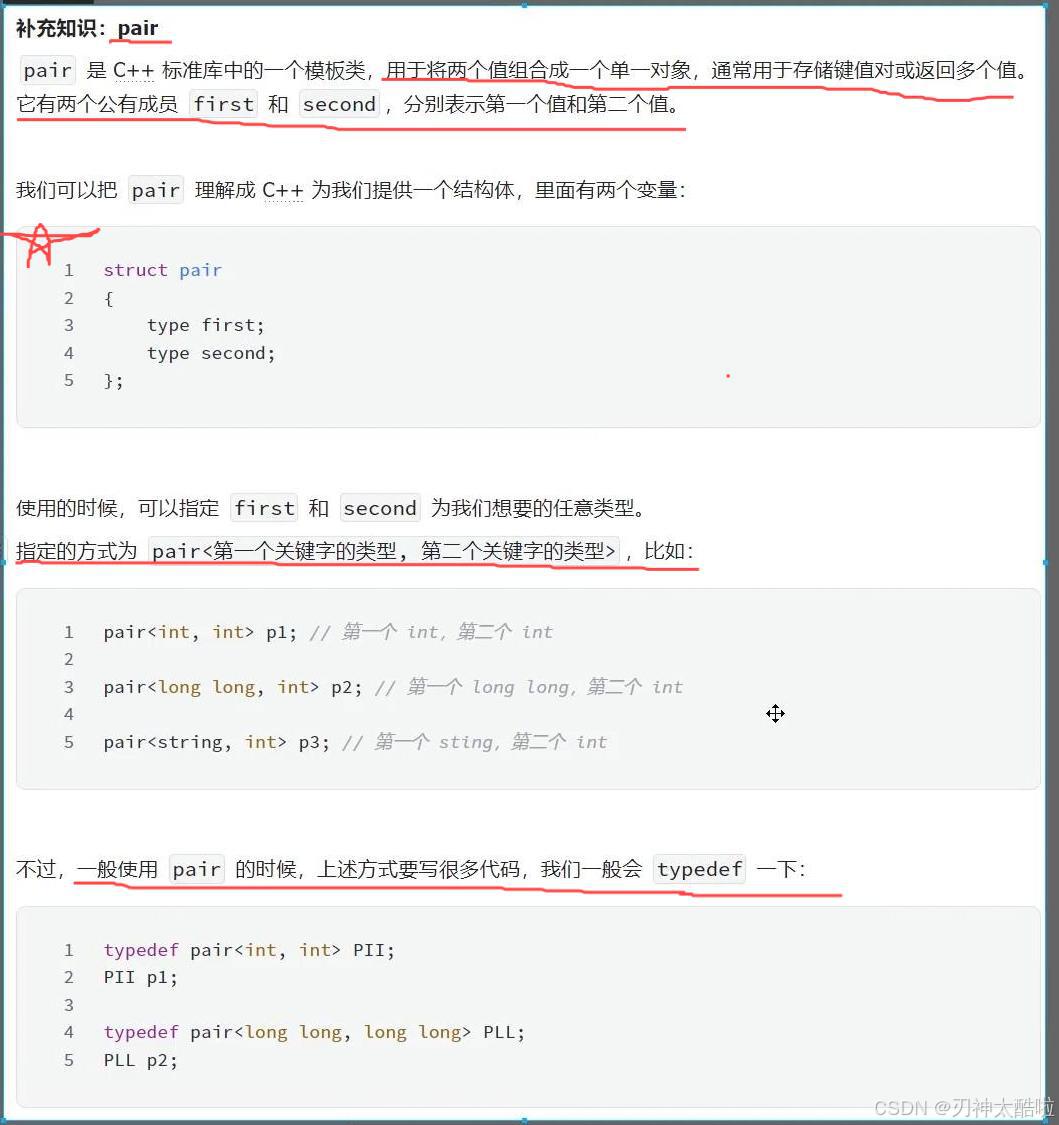
数据结构(蓝桥杯常考点)
数据结构 前言:这个是针对于蓝桥杯竞赛常考的数据结构内容,基础算法比如高精度这些会在下期给大家总结 数据结构 竞赛中,时间复杂度不能超过10的7次方(1秒)到10的8次方(2秒) 空间限制&#x…...

Tomcat+Servlet运行后出现404错误解决方案
TomcatServlet运行后出现404错误解决方案 一、错误效果复现 后续的解决方案,仅仅针对我遇到的情况。对不能涵盖大部分情况感到抱歉。 二、错误分析 先看看源代码? package com.example.secondclass.Servlet; import java.io.*; import jakarta.servl…...
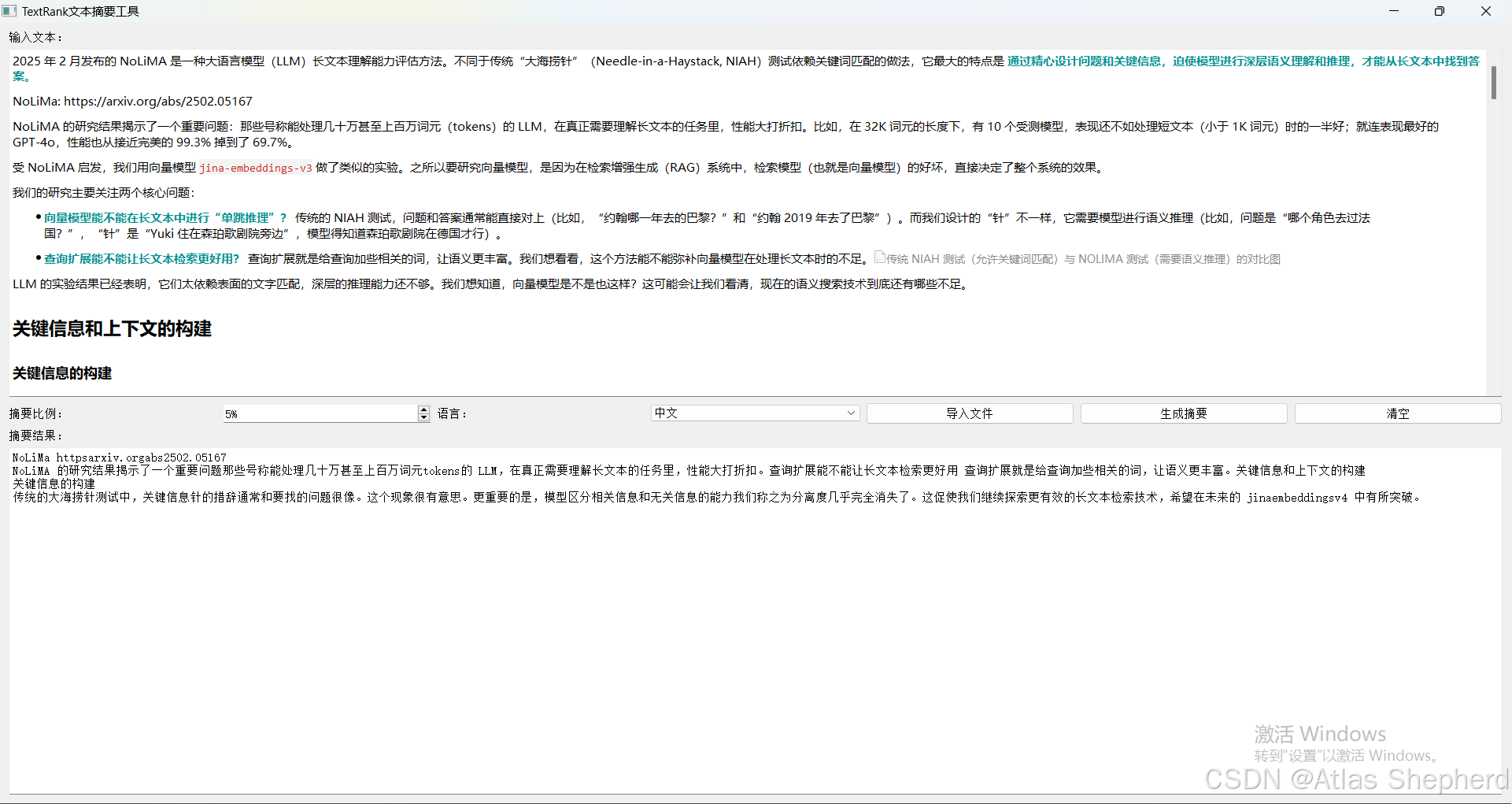
论文摘要生成器:用TextRank算法实现文献关键信息提取
我们基于python代码,使用PyQt5创建图形用户界面(GUI),同时支持中英文两种语言的文本论文文献关键信息提取。 PyQt5:用于创建GUI应用程序。 jieba:中文分词库,用于中文文本的处理。 reÿ…...

Flutter中网络图片加载显示Image.network的具体用法
Image.network的具体用法 Image.network 是 Flutter 中用于从网络加载图片的便捷方法。它基于 NetworkImage,可以快速加载并显示网络图片。以下是 Image.network 的具体用法和常见参数说明。 基本用法 最简单的用法是提供一个图片的 URL: dart 复制 …...
【HarmonyOS Next】鸿蒙应用故障处理思路详解
【HarmonyOS Next】鸿蒙应用崩溃处理思路详解 一、崩溃问题发现后定位 1. 崩溃现象: 常见的崩溃问题表现为,应用操作后白屏闪退,或者应用显示无响应卡死。 2.定位问题: 发现崩溃后,我们首先需要了解复现步骤&#x…...
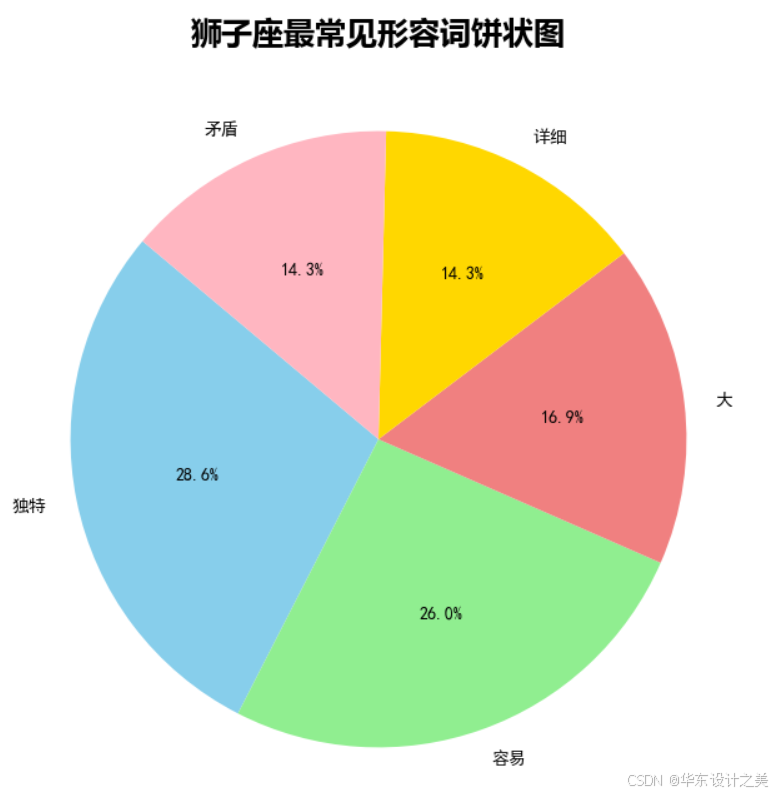
狮子座大数据分析(python爬虫版)
十二星座爱情性格 - 星座屋 首先找到一个星座网站,作为基础内容,来获取信息 网页爬取与信息提取 我们首先利用爬虫技术(如 Python 中的 requests 与 BeautifulSoup 库)获取页面内容。该页面(xzw.com/astro/leo/&…...
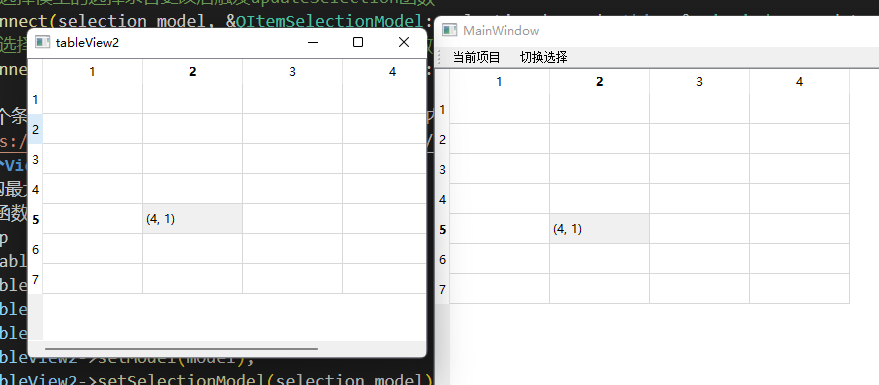
QT系列教程(18) MVC结构之QItemSelectionModel模型介绍
视频教程 https://www.bilibili.com/video/BV1FP4y1z75U/?vd_source8be9e83424c2ed2c9b2a3ed1d01385e9 QItemSelectionModel Qt的MVC结构支持多个View共享同一个model,包括该model的选中状态等。我们可以通过设置QItemSelectionModel,来更改View的选…...

git设置本地仓库和远程仓库
设置本地仓库和远程仓库是使用Git进行版本控制的基本操作。以下是详细步骤: 创建本地仓库 初始化本地仓库: 打开命令行工具(如Terminal或Git Bash)。导航到你希望创建Git仓库的项目文件夹。运行以下命令来初始化一个新的Git仓库&…...

openharmony中HDF驱动框架源码梳理-驱动加载流程
要想大概了解一个公司,我们可能只需要知道它的运行逻辑即可,例如我们只需要知道它有财务有研发有运营等,财务报销、研发负责产品等即可,但是如果想深入具体的了解的话我们就要了解都有什么部门(对象)、各部门都包含哪些职责(对象方…...

golang 高性能的 MySQL 数据导出
需求导出方式对比方案1:快照导出(耗时:1.5s)方案2: 偏移分页(耗时:4s)方案 3:普通分页(耗时:4min40s) 需求 导出 MySQL 数据 分析: 一次性 select 大量数据带来的问题 性能问题: 数据库负载:大量数据查询会增加数据库的CPU、内存和I/O负担ÿ…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
