动态规划,这将是你见过最详细的讲解
文章目录
- 一、为什么要讲动态规划呢?
- 二、什么是动态规划
- 三、感受一下递归算法、备忘录算法、动态规划
- 递归算法
- 带备忘录的递归解法(自定向下)
- 自底向上的动态规划
- 四、动态规划的解题套路
- 1. 穷举分析
- 2. 确定边界
- 3. 确定最优子结构
- 4. 写出状态转移方程
我建议直接看下面的参考文章,因为大佬的讲解非常到位,我这里做的笔记肯定是没那么详细的,这里只是给我自己做个记录
看一遍就理解:动态规划详解
算法-动态规划 Dynamic Programming–从菜鸟到老鸟
一、为什么要讲动态规划呢?
我们刷leetcode的时候,经常会遇到动态规划类型题目。动态规划问题非常非常经典,也很有技巧性,一般大厂都非常喜欢问。学就要学一些回报最大的知识
二、什么是动态规划
动态规划(英语:Dynamic programming,简称 DP),是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
以上定义来自维基百科,看定义感觉还是有点抽象。简单来说,动态规划其实就是,给定一个问题,我们把它拆成一个个子问题,直到子问题可以直接解决。然后呢,把子问题答案保存起来,以减少重复计算。再根据子问题答案反推,得出原问题解的一种方法。
相信看到这里,我们可以知道动态规划也用到HashMap集合,如果还不会,请看我另一篇博客,让你秒懂Java集合框架
动态规划核心思想
动态规划最核心的思想,就在于拆分子问题,记住过往,减少重复计算。然而我认为记不记住过往不重要,重要的是不要重复计算子问题就行了。例如自顶向下就需要备忘录,自底向上就不需要备忘录了。

我们来看下,网上比较流行的一个例子
A : “1+1+1+1+1+1+1+1 =?”
A : “上面等式的值是多少”
B : 计算 “8”
A : 在上面等式的左边写上 “1+” 呢?
A : “此时等式的值为多少”
B : 很快得出答案 “9”
A : “你怎么这么快就知道答案了”
A : “只要在8的基础上加1就行了”
A : “所以你不用重新计算,因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”
三、感受一下递归算法、备忘录算法、动态规划
leetcode原题:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。
有些小伙伴第一次见这个题的时候,可能会有点蒙圈,不知道怎么解决。其实可以试想:
要想跳到第10级台阶,要么是先跳到第9级,然后再跳1级台阶上去;要么是先跳到第8级,然后一次迈2级台阶上去。
同理,要想跳到第9级台阶,要么是先跳到第8级,然后再跳1级台阶上去;要么是先跳到第7级,然后一次迈2级台阶上去。
要想跳到第8级台阶,要么是先跳到第7级,然后再跳1级台阶上去;要么是先跳到第6级,然后一次迈2级台阶上去。
假设跳到第n级台阶的跳数我们定义为f(n),很显然就可以得出以下公式:
f(10) = f(9)+f(8)
f (9) = f(8) + f(7)
f (8) = f(7) + f(6)
…
f(3) = f(2) + f(1)
即通用公式为: f(n) = f(n-1) + f(n-2)
我们现在确定一下界限
通常设为为0和1,但是0代表还没有上阶梯,所以要从1开始。再根据公式f(n) = f(n-1) + f(n-2),可以知道界限需要设为1,2,并且f(1) = 1,f(2) = 2.
递归算法
class Solution {public int numWays(int n) {if(n == 1){return 1;}if(n == 2){return 2;}return numWays(n-1) + numWays(n-2);}
}
去leetcode提交一下,发现有问题,超出时间限制了

为什么超时了呢?递归耗时在哪里呢?先画出递归树看看:
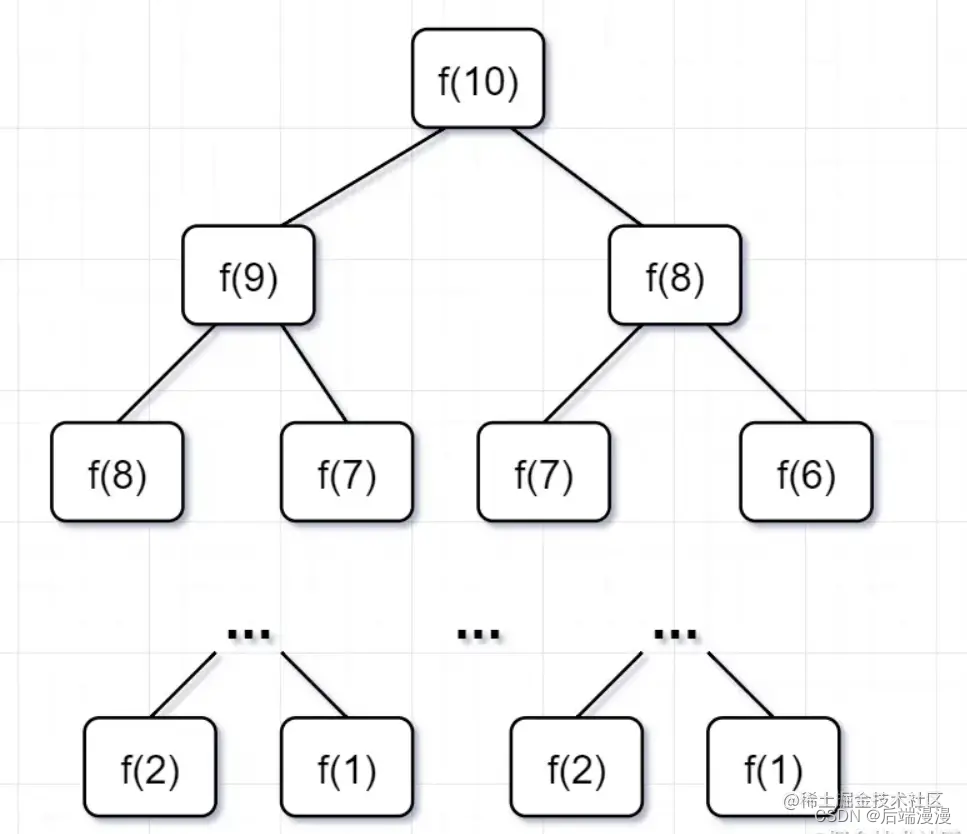
我们先来看看这个递归的时间复杂度吧:
递归时间复杂度 = 解决一个子问题时间*子问题个数
一个子问题时间 = f(n-1)+f(n-2),也就是一个加法的操作,所以复杂度是 O(1);
问题个数 = 递归树节点的总数,递归树的总节点 = 2n-1,所以是复杂度O(2n)。
因此,青蛙跳阶,递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n),就是指数级别的,爆炸增长的,如果n比较大的话,超时很正常的了。
既然存在大量重复计算,那么我们可以先把计算好的答案存下来,即造一个备忘录,等到下次需要的话,先去备忘录查一下,如果有,就直接取就好了,备忘录没有才开始计算,那就可以省去重新重复计算的耗时啦!这就是带备忘录的解法。
带备忘录的递归解法(自定向下)
一般使用一个数组或者一个哈希map充当这个备忘录。
第一步,f(10)= f(9) + f(8),f(9) 和f(8)都需要计算出来,然后再加到备忘录中,如下:

第二步, f(9) = f(8)+ f(7),f(8)= f(7)+ f(6), 因为 f(8) 已经在备忘录中啦,所以可以省掉,f(7),f(6)都需要计算出来,加到备忘录中~
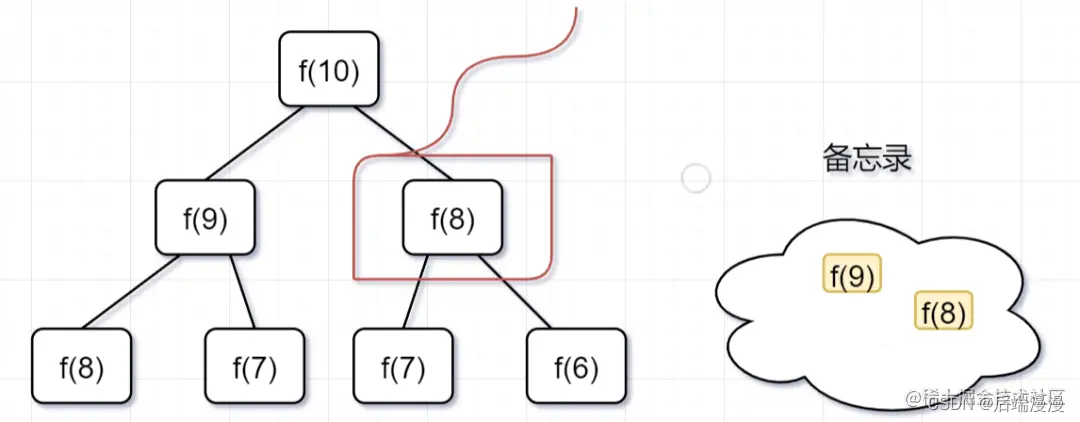
第三步, f(8) = f(7)+ f(6),发现f(8),f(7),f(6)全部都在备忘录上了,所以都可以剪掉。
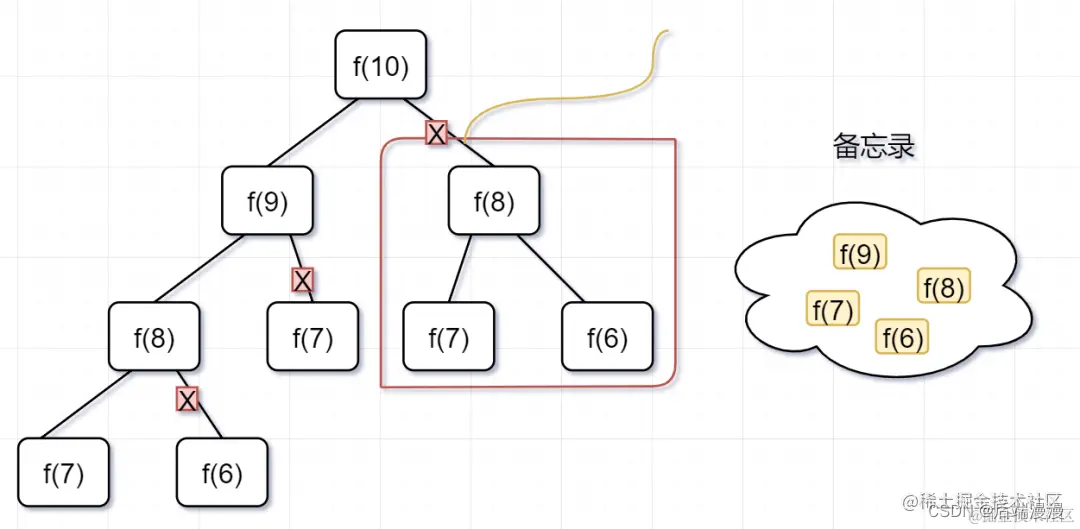
所以呢,用了备忘录递归算法,递归树变成光秃秃的树干咯,如下:
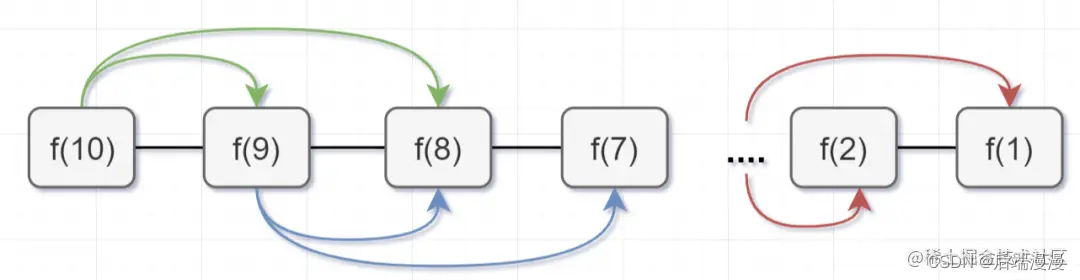
带备忘录的递归算法,子问题个数=树节点数=n,解决一个子问题还是O(1),所以带备忘录的递归算法的时间复杂度是O(n)。接下来呢,我们用带备忘录的递归算法去撸代码,解决这个青蛙跳阶问题的超时问题咯~,代码如下:
public class Solution {//使用哈希map,充当备忘录的作用Map<Integer, Integer> tempMap = new HashMap();public int numWays(int n) {// n = 0 也算1种if (n == 0) {return 1;}if (n <= 2) {return n;}//先判断有没计算过,即看看备忘录有没有if (tempMap.containsKey(n)) {//备忘录有,即计算过,直接返回return tempMap.get(n);} else {// 备忘录没有,即没有计算过,执行递归计算,并且把结果保存到备忘录map中,对1000000007取余(这个是leetcode题目规定的)tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007);return tempMap.get(n);}}
}
自底向上的动态规划
动态规划跟带备忘录的递归解法基本思想是一致的,都是减少重复计算,时间复杂度也都是差不多。但是呢:
带备忘录的递归,是从f(10)往f(1)方向延伸求解的,所以也称为自顶向下的解法。
动态规划从较小问题的解,由交叠性质,逐步决策出较大问题的解,它是从f(1)往f(10)方向,往上推求解,所以称为自底向上的解法。
动态规划有几个典型特征,最优子结构、状态转移方程、边界、重叠子问题,在青蛙跳阶问题中:
- f(n-1)和f(n-2) 称为 f(n) 的最优子结构
- f(n)= f(n-1)+f(n-2)就称为状态转移方程
- f(1) = 1, f(2) = 2 就是边界啦
- 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。
public class Solution {public int numWays(int n) {if (n<= 1) {return 1;}if (n == 2) {return 2;}int a = 1;int b = 2;int temp = 0;for (int i = 3; i <= n; i++) {temp = (a + b)% 1000000007;a = b;b = temp;}return temp;}}
四、动态规划的解题套路
什么样的问题可以考虑使用动态规划解决呢?
如果一个问题,可以把所有可能的答案穷举出来,并且穷举出来后,发现存在重叠子问题,就可以考虑使用动态规划。
比如一些求最值的场景,如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等,都是动态规划的经典应用场景。
动态规划的解题思路:
- 穷举分析,即做树状图找规律
- 确定边界
- 去欸的那个最优子结构
- 写出状态转移方程
1. 穷举分析
当台阶数是1的时候,有一种跳法,f(1) =1
当只有2级台阶时,有两种跳法,第一种是直接跳两级,第二种是先跳一级,然后再跳一级。即f(2) = 2;
当台阶是3级时,想跳到第3级台阶,要么是先跳到第2级,然后再跳1级台阶上去,要么是先跳到第 1级,然后一次迈 2 级台阶上去。所以f(3) = f(2) + f(1) =3
当台阶是4级时,想跳到第3级台阶,要么是先跳到第3级,然后再跳1级台阶上去,要么是先跳到第 2级,然后一次迈 2 级台阶上去。所以f(4) = f(3) + f(2) =5
当台阶是5级时…
2. 确定边界
通过穷举分析,我们发现,当台阶数是1的时候或者2的时候,可以明确知道青蛙跳法。f(1) =1,f(2) = 2,当台阶n>=3时,已经呈现出规律f(3) = f(2) + f(1) =3,因此f(1) =1,f(2) = 2就是青蛙跳阶的边界。
3. 确定最优子结构
n>=3时,已经呈现出规律 f(n) = f(n-1) + f(n-2) ,因此,f(n-1)和f(n-2) 称为 f(n) 的最优子结构。什么是最优子结构?有这么一个解释:
4. 写出状态转移方程
通过前面3步,穷举分析,确定边界,最优子结构,我们就可以得出状态转移方程啦
相关文章:

动态规划,这将是你见过最详细的讲解
文章目录一、为什么要讲动态规划呢?二、什么是动态规划三、感受一下递归算法、备忘录算法、动态规划递归算法带备忘录的递归解法(自定向下)自底向上的动态规划四、动态规划的解题套路1. 穷举分析2. 确定边界3. 确定最优子结构4. 写出状态转移…...

【服务器数据恢复】FreeNAS层UFS2文件系统数据恢复案例
服务器数据恢复环境: Dell存储服务器,采用esxi虚拟化系统,esxi虚拟化系统里有3台虚拟机;上层iSCSI使用FreeNAS构建,通过iSCSI方式实现FCSAN功能;FreeNAS层采用UFS2文件系统。 esxi虚拟化系统里有3台虚拟机中…...

Zookeeper安装和基本使用
目录标题一、下载二、安装三、启动客户端测试四、使用zk一、下载 注意:自zk3.5.5版本以后,已编译的jar包,尾部有bin,应该使用的是apache-zookeeper-3.8.0-bin.tar.gz。,因此在下载高版本时,因该下载后缀带b…...
字节面试惨败,闭关修炼再战美团(Android 面经~)
作者:王旭 前言 本人从事Android 开发已经有5年了,受末日寒气影响,被迫在家休整,事后第一家选择字节跳动面试,无奈的被面试官虐得“体无完肤”,好在自己并未气馁,于是回家开始回家进行闭关修炼…...
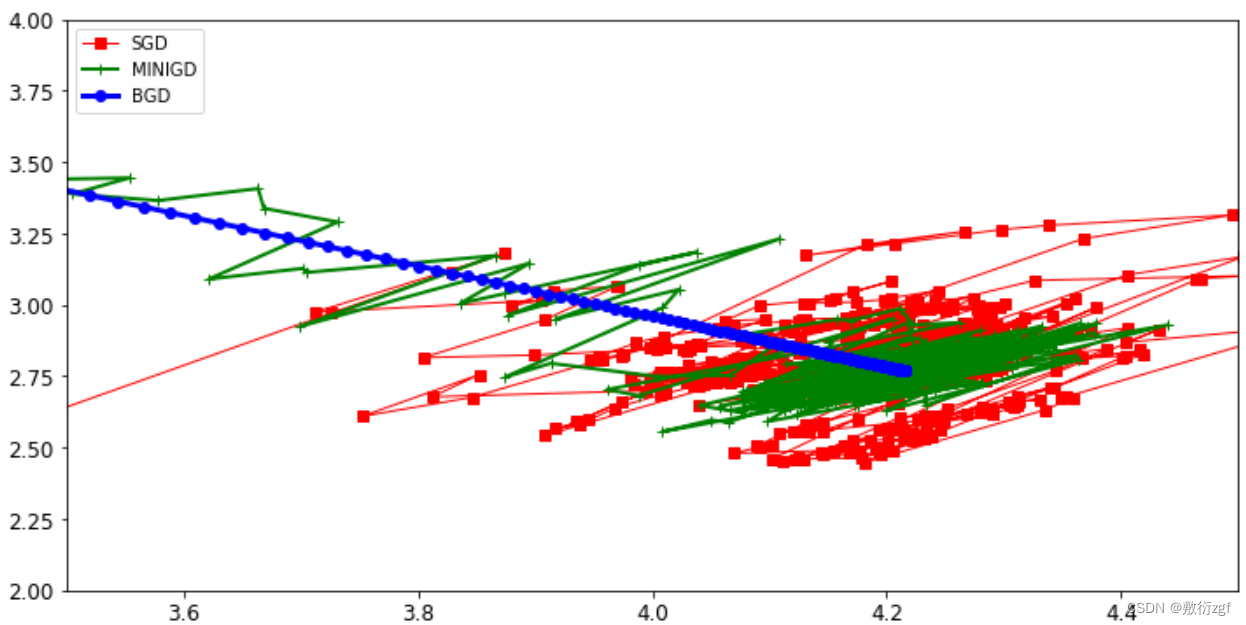
【机器学习实战】七、梯度下降
梯度下降 一、线性回归 线性回归算法推导过程可以基于最小二乘法直接求解,但这并不是机器学习的思想,由此引入了梯度下降方法。本文讲解其中每一步流程与实验对比分析。 1.初始化 import numpy as np import os %matplotlib inline import matplotli…...

什么是极速文件传输,极速文件传输如何进行大文件传输
当谈到大文件传输时,人们总是担心大数据文件的大小以及将它们从一个位置交换到另一个位置需要多长时间。由于数据捕获高分辨率视频和图像的日益复杂,文件的大小不断增加。数据工作流在地理上变得越来越分散。在一个位置生成的文件在其他位置处理或使用。…...

Spring Boot 日志
目录 1.概述 2.切换日志实现 3.使用 3.1.日志级别 3.3.日志离线 3.4.详细定制 1.概述 由一些历史原因,JAVA领域存在有很多日志框架,如Log4j、Logback、log4j2。 log4j是Java日志框架的元老,在log4j被Apache Foundation收入门下之后&a…...

好用的研发管理看板工具有哪些?10款主流看板管理软件盘点
10大企业看板工具软件:1.软件开发项目看板 PingCode;2.通用看板软件 Worktile;3.开源看板软件 Wekan;4.免费看板软件 Trello;5.个人和小团队的看板软件 Todoist ;6.开源免费看 Kanboard;7.面向个…...
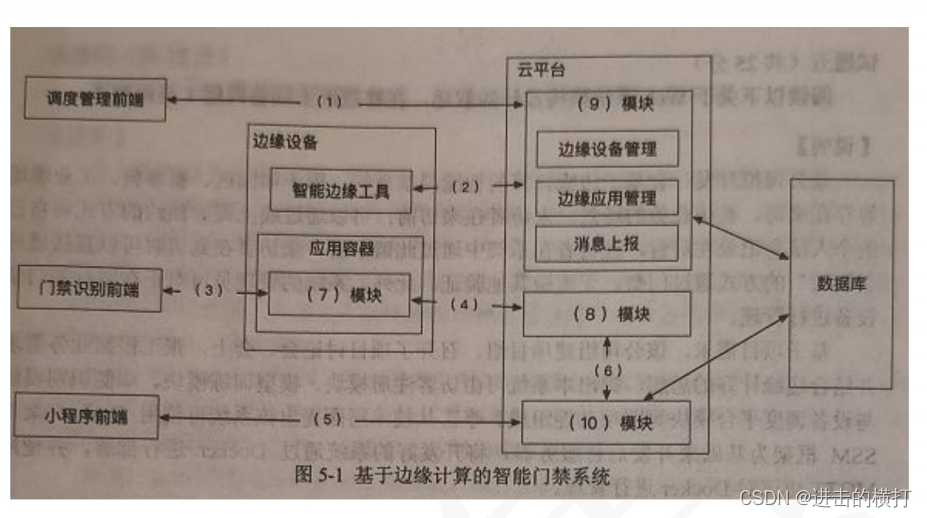
【软考系统架构设计师】2022下案例分析历年真题
【软考系统架构设计师】2022下案例分析历年真题 【软考系统架构设计师】2022下案例分析历年真题【软考系统架构设计师】2022下案例分析历年真题2022下案例分析历年真题第一题(25分)2022下案例分析历年真题第二题(25分)2022下案例分…...

Java skill - @JsonAlias 和 @JsonProperty
Java skill - JsonAlias 和 JsonPropertyJava skill系列目录:JsonAlias 和 JsonProperty使用 JsonProperty 的麻烦场景:使用 JsonAlias 应对麻烦场景:Java skill系列目录: 【Java skill - 统计耗时用StopWatch】 【Java skill - …...
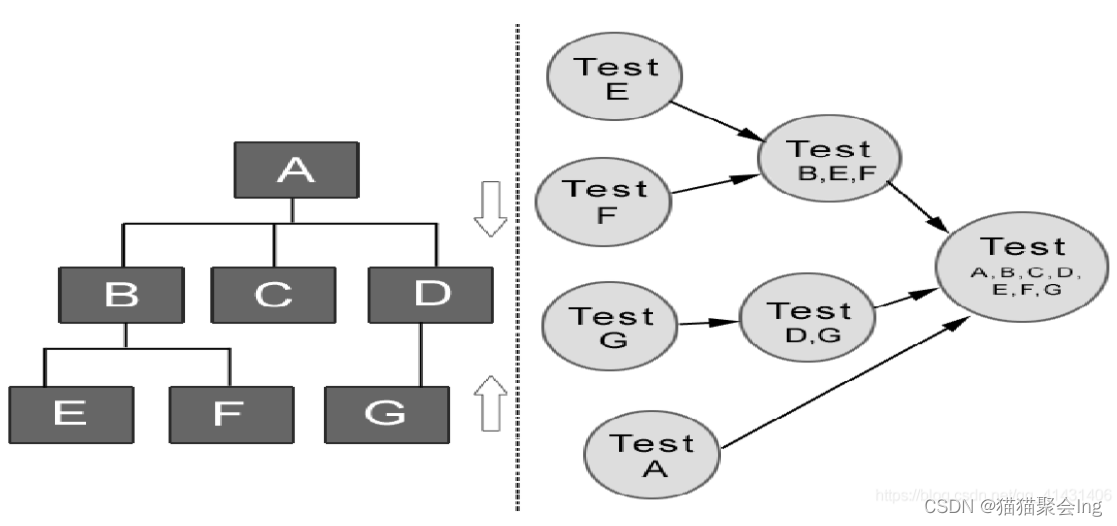
【实际开发18】- 静态 3
目录 1. 调试与评估 2. 单元测试的管理 1. 单元测试的文档 3. 系统集成的模式与方法 1. 集成测试前的准备 2. 集成测试的模式 3. 大棒集成方法 ( Big-bang Integration) 4. 自顶向下和自底向上集成方法 1. 自顶向下法 ( Top-down Integration ) 2. 自底向上法 ( Bott…...

【swagger2】开发api文档
文章目录一、swagger2 简介背景Open API ???swagger2的作用swagger2常用工具组件:二、Springfox三、springBoot使用swagger2(简单示例)四、Swagger-UI使用五、配置文件1、配置类:给docket上下文配置api描述信息2、配置类&#…...

Github 上如何提交 pull request
什么是复刻(forking)? 我们可以通过复刻操作将喜爱的仓库保存自己的Github账户中,以便独立地对其进行操作。 通过复刻,我们可以得到包含完整版本历史的目标仓库的实例,之后可以对复刻得到的仓库进行任意操作而不会影响…...

Redis面试知识
概述 Redis 是速度非常快的非关系型(NoSQL)内存键值数据库,可以存储键和五种不同类型的值之间的映射。 键的类型只能为字符串,值支持五种数据类型:字符串、列表、集合、散列表、有序集合。 Redis 支持很多特性,例如将内存中的数据持久化到硬盘中,使用复制来扩展读性能…...

Spring面试重点(四)——Spring事务
Spring事务 事务的方式 spring中使用事务有两种方式,一种是编程式事务,一种是声明式事务。编程式事务推荐使用TransactionTemplate,实现TransactionCallback接口,需要编码实现;声明式事务只需要在函数增加注解Transa…...

♡ — MySQL 存储引擎
MySQL 存储引擎架构 MySQL 存储引擎采用的是插件式架构,支持多种存储引擎,我们甚至可以为不同的数据库设置不同的存储引擎以适应不同场景的需要;存储引擎是基于表的,而不是数据库。 MyISAM 和 InnoDB 的区别 MySQL 5.5 之前&am…...
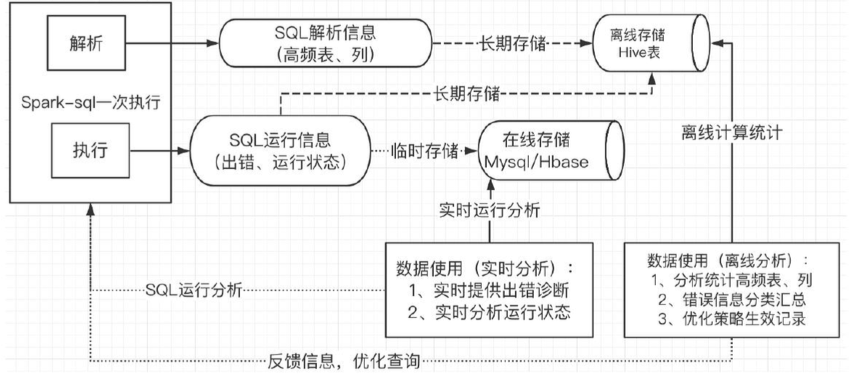
大数据技术架构(组件)34——Spark:Spark SQL--Optimize
2.2.3、Optimize2.2.3.1、SQL3.3.1.1、RB1、Join选择在Hadoop中,MR使用DistributedCache来实现mapJoin。即将小文件存放到DistributedCache中,然后分发到各个Task上,并加载到内存中,类似于Map结构,然后借助于Mapper的迭…...
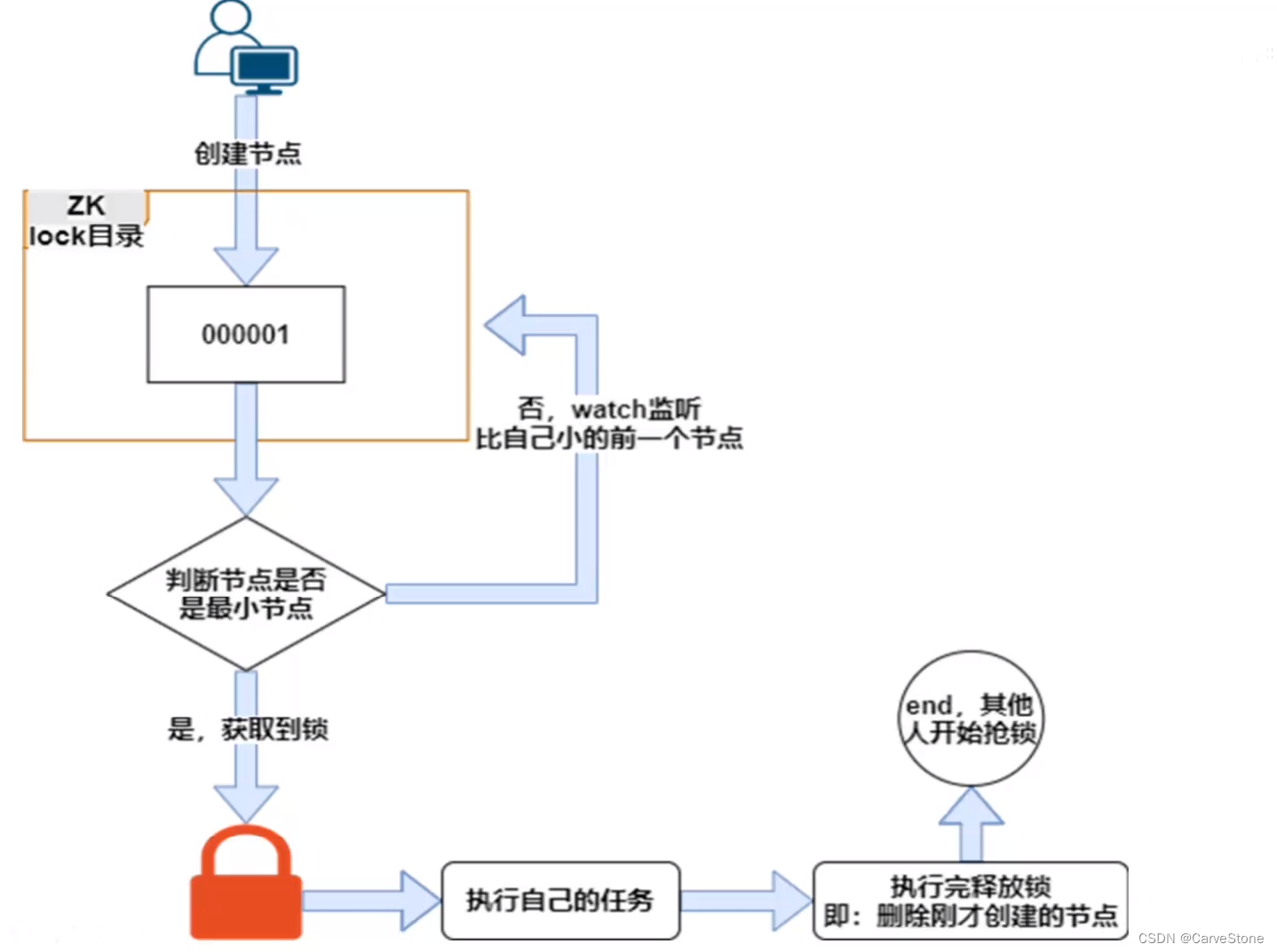
Zookeeper实现分布式锁
文章目录ZK节点类型watch监听机制Zookeeper实现分布式锁锁原理创建锁的过程释放锁的过程ZK锁的种类代码实现Zookeeper是一个开源的分布式协调服务,是一个典型的分布式数据一致性解决方案。 分布式应用程序可以基于Zookeeper实现诸如数据发布/订阅,负载均…...

MFC 添加重新启动管理器支持
重启管理器是添加到 Visual Studio for Windows Vista 或更高版本操作系统的功能 如果发生意外关闭或重启,重新启动管理器将为你的应用程序添加支持。 重新启动管理器的行为取决于应用程序的类型。 如果你的应用程序是文档编辑器,则重新启动管理器让应用…...

一文带你深刻的进入Python,并且了解Python的优缺点
最近几年Python被吹的神乎其神,很多同学都不清楚Python到底能干什么?就盲目去学习Python,今天我就Python的应用领域来简单盘点一下,让想学习Python 的同学找对方向不迷茫。 2. Python 的特点 这里就谈谈自己的看法,首先 Python是…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
