js浮点数四则运算精度丢失以及toFixed()精度丢失解决方法
js浮点数四则运算精度丢失以及tofixed精度丢失解决方法
- 一、js浮点数计算精度丢失的一些例子
- 1、四则运算精度丢失:
- 2、toFixed() 四舍五入精度丢失:
- 二、浮点数计算精度丢失的原因
- 三、解决办法
- 1、使用 big.js(如果有大量连续的计算推荐使用)
- 2、解决四则运算精度丢失问题
- 方法1:没有具体要求保留几位小数的,最简单的方法是直接用 `toFixed()`
- 方法2:有具体要求精确到第几位,用`科学计数法`对运算结果进行四舍五入
- 实现原理:
- 使用方法:
- 3、解决 toFixed() 精度丢失问题:重写 toFixed 方法(重点!!!!)
- 四、判断小数是否相等
- 五、其他由浮点数引起的问题
一、js浮点数计算精度丢失的一些例子
1、四则运算精度丢失:
0.1+0.2 = 0.30000000000000004 0.3 - 0.2 = 0.0999999999999999810.22*100 = 1022.00000000000012.4/0.8 = 2.999999999999999632.2*100 = 3220.000000000000532.2*1000 = 32200.000000000004(32.2*100 + 3.14*100) / 100 = 35.34 // 这里的精度怎么又不丢失了?32.3*100 = 3229.999999999999532.3*1000 = 32299.999999999996...
2、toFixed() 四舍五入精度丢失:
(1.335).toFixed(2); // '1.33'
(6.265).toFixed(2); // '6.26'
二、浮点数计算精度丢失的原因
js采用64位浮点数表示法(几乎所有现代编程语言所采用),这是一种二进制表示法。二进制浮点数表示法并不能精确表示类似 0.1 这样简单的数字。
这个问题不只在js中才会出现,在任何使用二进制浮点数的编程语言中都会出现。
JavaScript的未来版本或许会支持十进制数字类型以避免精度丢失的问题。
三、解决办法
1、使用 big.js(如果有大量连续的计算推荐使用)
- 既解决了浮点数计算精度丢失问题,又解决了 toFixed() 四舍五入精度丢失问题。
big.js是big.js,bignumber.js,decimal.js三姐妹中功能最少的,但也是体积最小的,压缩版只有3k,对于处理js精度丢失已经足够用了。
import Big from 'big.js'// 运算const plus = Big(0.1).plus(0.2); // 加const minus = Big(0.3).minus(0.1); // 减const mul = Big(10.22).times(100); // 乘const div = Big(2.4).div(0.8); // 除// toFixedconst fixed = new Big(6.265).toFixed(2); // 6.27console.log(plus.toNumber(),minus.toNumber(),mul.toNumber(),div.toNumber())// 0.3 0.2 1022 3
2、解决四则运算精度丢失问题
方法1:没有具体要求保留几位小数的,最简单的方法是直接用 toFixed()
从上面四则运算精度丢失的例子可以看到,四则运算的精度丢失主要会出现很多位 0 或很多位 9。
function precision(val) {return +val.toFixed(8);
}precision(0.1 + 0.2)
方法2:有具体要求精确到第几位,用科学计数法对运算结果进行四舍五入
MDN 已经给出了具体代码(也是利用“科学计数法”扩大 10 的 n 次不会出现精度丢失的特性):
function round(number, precision) {return Math.round(+number + 'e' + precision) / Math.pow(10, precision);
}round(1.005, 2); //1.01
round(1.002, 2); //1
或者:
/*** Decimal adjustment of a number.** @param {String} type The type of adjustment.* @param {Number} value The number.* @param {Integer} exp The exponent (the 10 logarithm of the adjustment base).* @returns {Number} The adjusted value.*/
function decimalAdjust(type, value, exp) {// If the exp is undefined or zero...if (typeof exp === 'undefined' || +exp === 0) {return Math[type](value);}value = +value;exp = +exp;// If the value is not a number or the exp is not an integer...if (isNaN(value) || !(typeof exp === 'number' && exp % 1 === 0)) {return NaN;}// Shiftvalue = value.toString().split('e');value = Math[type](+(value[0] + 'e' + (value[1] ? +value[1] - exp : -exp)));// Shift backvalue = value.toString().split('e');value = +(value[0] + 'e' + (value[1] ? +value[1] + exp : exp));return value;
}export default {round: (value, exp) => {return decimalAdjust('round', value, exp);},floor: (value, exp) => {return decimalAdjust('floor', value, exp);},ceil: (value, exp) => {return decimalAdjust('ceil', value, exp);}
};
实现原理:
比如 1022.0000000000001 要保留2位小数,先用 e2 把这个数扩大 100 倍,
再用 Math.round(), Math.floor(), Math.ceil() 取整,然后再用 e-2 缩小回来。
使用方法:
Decimal.round(val, precision)console.log(Decimal.round(1.13265, -3)) //1.133
console.log(Decimal.round(3.17, -3)) //3.17
console.log(Decimal.round(0.1+0.2, -3)) //0.3
console.log(Decimal.round(3.17)) //3
console.log(Decimal.round(3.17, 0)) //3
console.log(Decimal.round(31216, 1)) //31220
console.log(Decimal.round(31213, 2)) //31200
precision 可选值:不传,0,负数,正数。
- 不传、0: 精确到整数。
- 正数: 1就是个位为0,十位是个位四舍五入的值。
- 负数: 精确到小数点后几位
3、解决 toFixed() 精度丢失问题:重写 toFixed 方法(重点!!!!)
function toFixed(number, precision = 2) {number = Math.round(+number + 'e' + precision) / Math.pow(10, precision) + '';let s = number.split('.');if ((s[1] || '').length < precision) {s[1] = s[1] || '';s[1] += new Array(precision - s[1].length).fill('0').join('');}return s.join('.');
}toFixed(6) // '6.00'
四、判断小数是否相等
function epsEqu(x,y) { return Math.abs(x - y) < Math.pow(2, -52);// 因为 Number.EPSILON === Math.pow(2, -52),所以也可以这么写:// return Math.abs(x - y) < Number.EPSILON;
}
// 举例
0.1 + 0.2 === 0.3 // false
epsEqu(0.1 + 0.2, 0.3) // true
小数比较时,要给它一个误差范围,在误差范围内的都算相等。
五、其他由浮点数引起的问题
parseInt(0.0000008) // -> 8
相关文章:
精度丢失解决方法)
js浮点数四则运算精度丢失以及toFixed()精度丢失解决方法
js浮点数四则运算精度丢失以及tofixed精度丢失解决方法一、js浮点数计算精度丢失的一些例子1、四则运算精度丢失:2、toFixed() 四舍五入精度丢失:二、浮点数计算精度丢失的原因三、解决办法1、使用 big.js(如果有大量连续的计算推荐使用&…...

高姿态下的面部表情识别系统
效果展示: python表情、性别识别面部表情识别 (FER) 在计算机安全、神经科学、心理学和工程学方面有大量应用。由于其非侵入性,它被认为是打击犯罪的有用技术。然而,FER 面临着几个挑战,其中最严重的是它在严重的头部姿势下的预测…...

English Learning - Day59 作业打卡 2023.2.13 周一
English Learning - Day59 作业打卡 2023.2.13 周一引言1. 我有一些急事要处理。2. 这个孩子无忧无虑。3. 那个骑在白马上的姑娘是我姐姐。4. 对方正在给我们公司施加压力迫使我们降价。5. 我的医生告诉我要少吃垃圾食品。6. 我从来不熬夜。7.我早就想跟你聊一聊了。8.我一定不…...
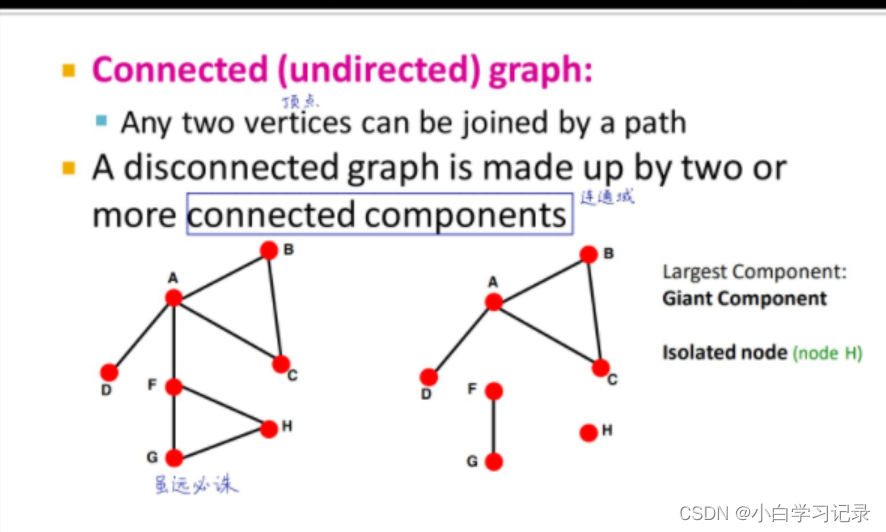
图机器学习
图机器学习1、图机器学习导论1.1图神经网络与普通神经网络的异同2、图的基本表示和特征工程2.1 图的基本表示2.1.1 图的本体设计2.1.2 图的种类2.1.3节点连接数(度)2.1.4图的基本表示(邻接矩阵)节点数量少使用2.1.5图的基本表示&a…...
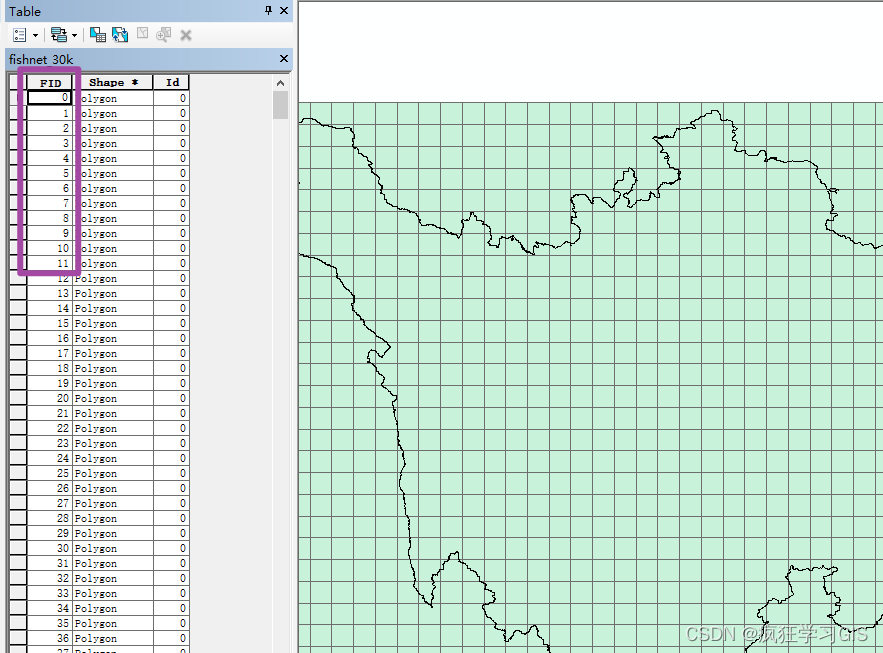
ArcGIS中ArcMap创建渔网Create Fishnet:生成指定大小的格网矢量文件
本文介绍在ArcMap软件中,通过“Create Fishnet”工具创建渔网,从而获得指定大小的矢量格网数据的方法。 首先,我们在创建渔网前,需要指定渔网覆盖的范围。这里我们就以四川省为例,在这一范围内创建渔网;其中…...

TensorRT中的自定义层
TensorRT中的自定义层 文章目录TensorRT中的自定义层9.1. Adding Custom Layers Using The C API9.1.1. Example: Adding A Custom Layer With Dynamic Shape Support Using C重要提示:覆盖检查索引小于pos的连接的格式/类型,但绝不能检查索引大于pos的连…...
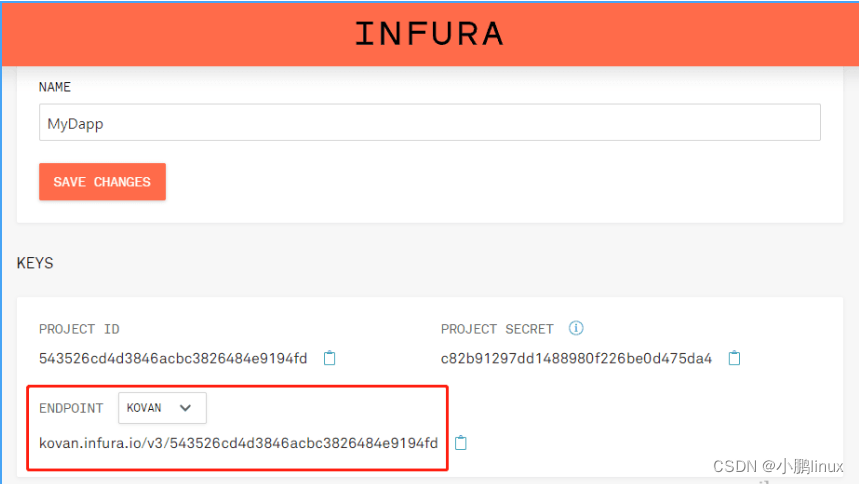
部署智能合约到公链
🍁博主简介: 🏅云计算领域优质创作者 🏅2022年CSDN新星计划python赛道第一名 🏅2022年CSDN原力计划优质作者 🏅阿里云ACE认证高级工程师 🏅阿里云开发者社区专…...
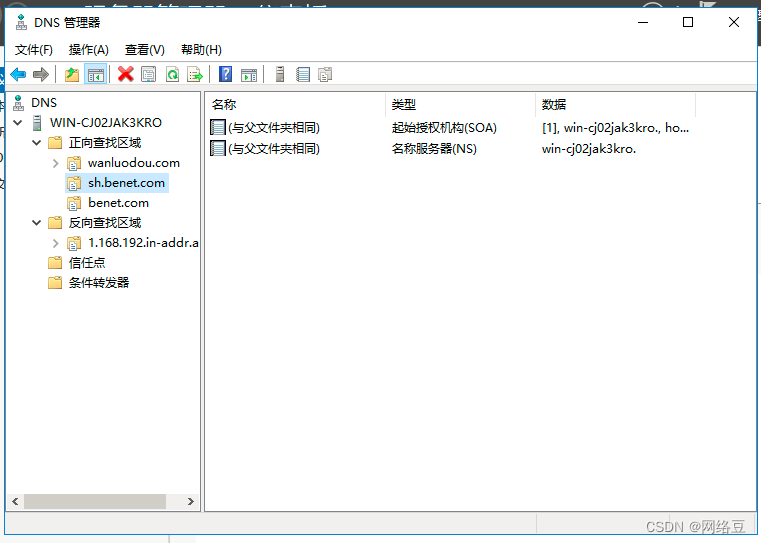
Windows server——部署DNS服务(3)
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.管理DNS服务 1.子域 案例 2. 委派 案例 1)添加主机记录 …...
9. QML_OpenGL--2. 在QQuick中搭建加载OpenGL框架
1. 说明: OPenGL一般在 QtWidget 中使用,但目前使用 QML 做界面开发是一种趋势,同时在QML中使用OPenGL进行渲染也是十分必要,文章简单介绍如何在QML中使用 OPenGL,搭建了一种基本的框架。整体思路和在 QtWidget 中类似…...
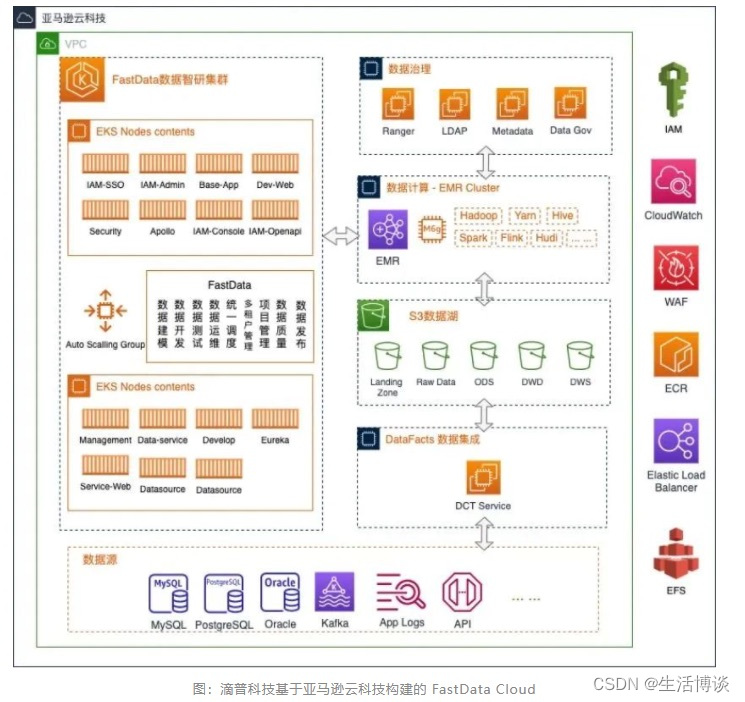
亚马逊云科技携手滴普科技,打造数据智能新标杆
随着企业数字化转型的不断深入,数据对于业务的价值和重要性也逐渐凸显。越来越多企业意识到,只有不断提升底层数据基础平台的性能和能力,才能构建数据驱动的业务,增强企业核心竞争力。作为湖仓一体数据智能基础软件独角兽企业&…...

CGO 跨平台静态编译
什么是跨平台编译? 跨平台编译:即交叉编译,是在一个平台上生成另一个平台上的可执行文件。所谓平台,实际上包含两个概念:体系架构(Architecture)、操作系统 (Operating System)。同一个体系架构可以运行不同…...

股票买卖接口怎么来的?
现在股票买卖接口主要是在线上研发,有专业的开发团队进行源码开发和完善,但是,常常会在开发过程中出现问题,也就是遇到一些特殊的情况需要及时处理,那么股票买卖接口怎么开发实现出来的?一、股票买卖接口开…...

【Python学习笔记】29.Python3 面向对象
前言 Python从设计之初就已经是一门面向对象的语言,正因为如此,在Python中创建一个类和对象是很容易的。本章节我们将详细介绍Python的面向对象编程。 Python3 面向对象 如果你以前没有接触过面向对象的编程语言,那你可能需要先了解一些面…...
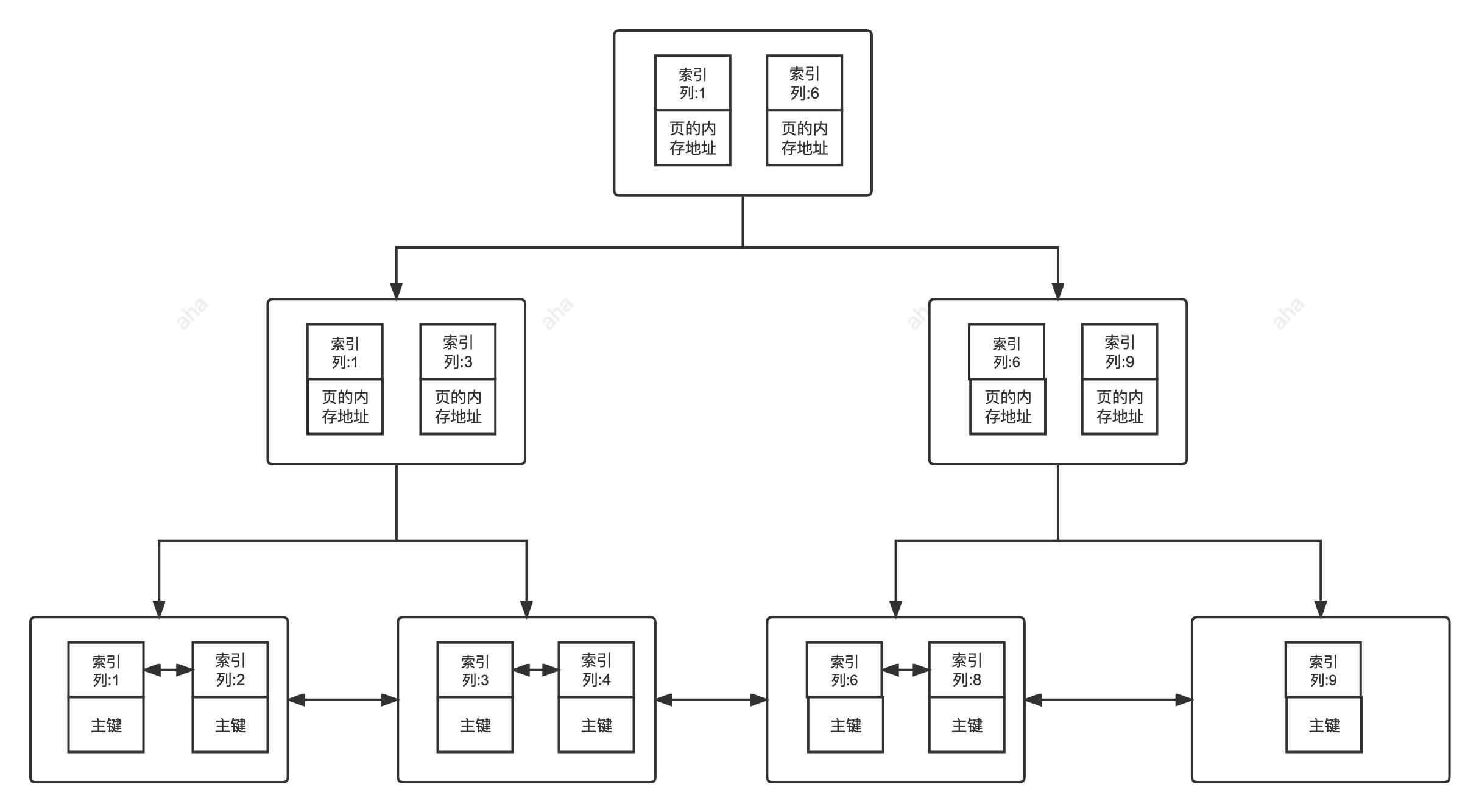
MySQL 索引
索引 索引是一种用于快速查询和检查数据的数据结构,其本质可以看成是一种排好序的数据结构。理解:索引的作用就相当于书的目录📚,可以根据目录快速定位到想要查看的位置。常见的索引结构:B Tree、B Tree、Hash、红黑树…...

学会使用LoadRunner录制脚本
1.LoadRunner安装 https://blog.csdn.net/weixin_48584088/article/details/129012469 2.Loadrunner的基本概念 LoadRunner是一种适用于许多软件体系架构的自动负载测试工具,从用户关注的响应时间、吞吐量, 并发用户和性能计数器等方面来衡量系统的性…...
产品经理必看的高效产品文档撰写指南
对于企业来说,如何推广自己的产品是一个非常重要的话题,而其中必要的就是创建企业产品宣传册,这对于产品宣传非常重要,尤其是一些大公司,非常重视这种产品展示方式。因为它可以更完整地展现产品,撰写一份合…...
Prometheus 的介绍和安装
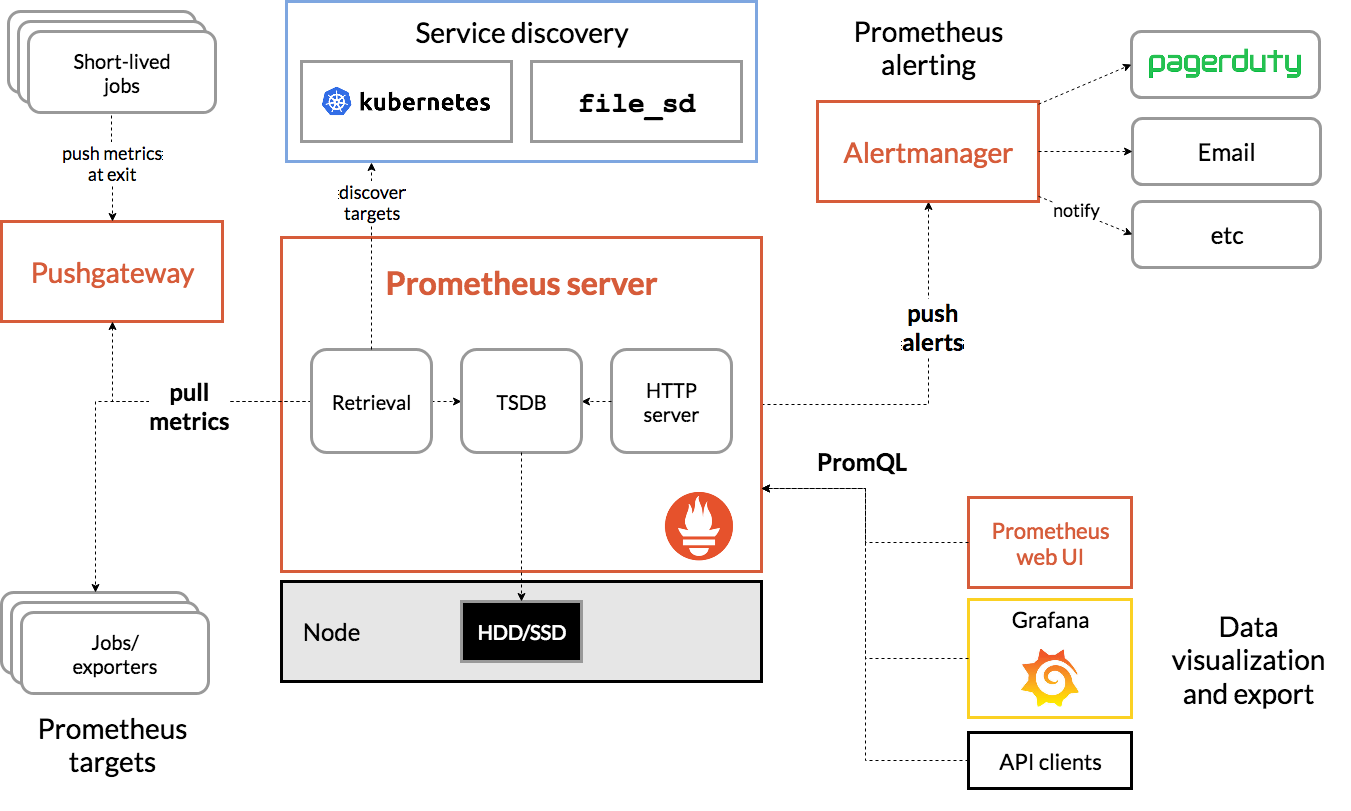
介绍 Prometheus 是一个开源的监控和报警系统,最初由SoundCloud于2012年创建,随着越来越多的公司采用Prometheus以及非常活跃的社区,Prometheus于2016年加入云原生基金会,成为Kubernetes之后的第二个托管项目,并于2018年毕业。 特点 通过PromQL来对基于指标名称和键值对…...

ViewModel快速上手1-原生kotlin
ViewModel 原生支持 kotlin 案例 基本案例 viewmodel 是为了保存当当前 activity 切出或者销毁时,如何保存数据,以便下一次创建新的 activity 时进行调用 首先引入 lifecycle 依赖 implementation androidx.lifecycle:lifecycle-extensions:2.2.0 之后…...
Flutter(一)介绍、Dart语言简介
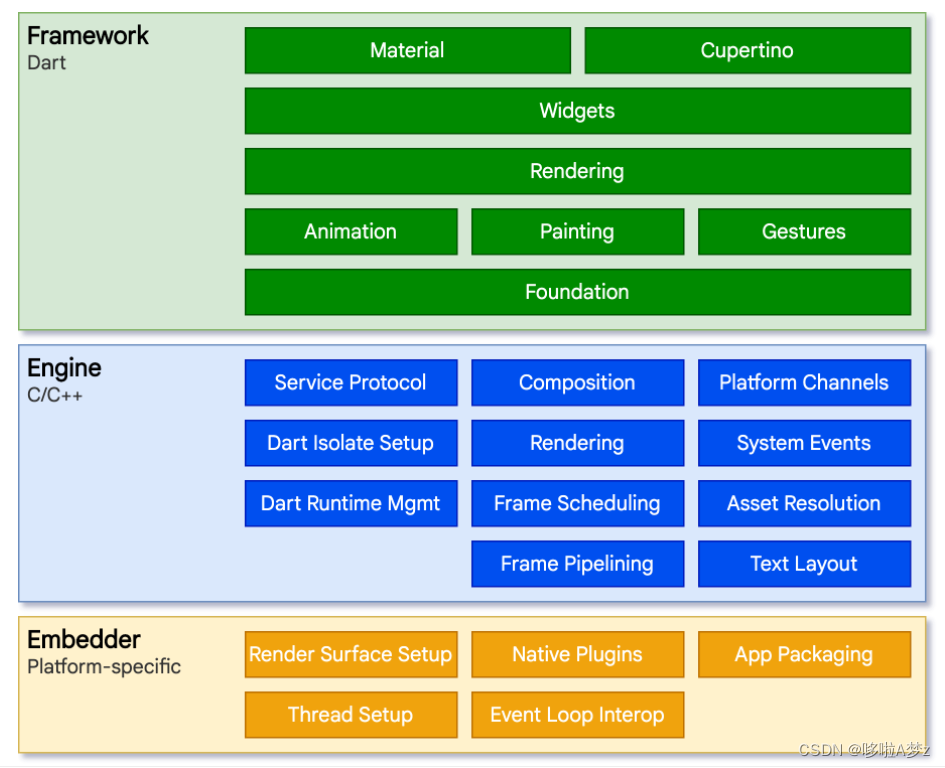
Flutter介绍 纯原生开发主要面临动态化更新和开发成本两个问题,而针对这两个问题,诞生了一些跨平台的动态化框架 跨平台技术简介 Flutter 是 Google 推出并开源的移动应用开发框架,主打跨平台、高保真、高性能。开发者可以通过 Dart 语言开…...
【数据结构】---顺序表的实现
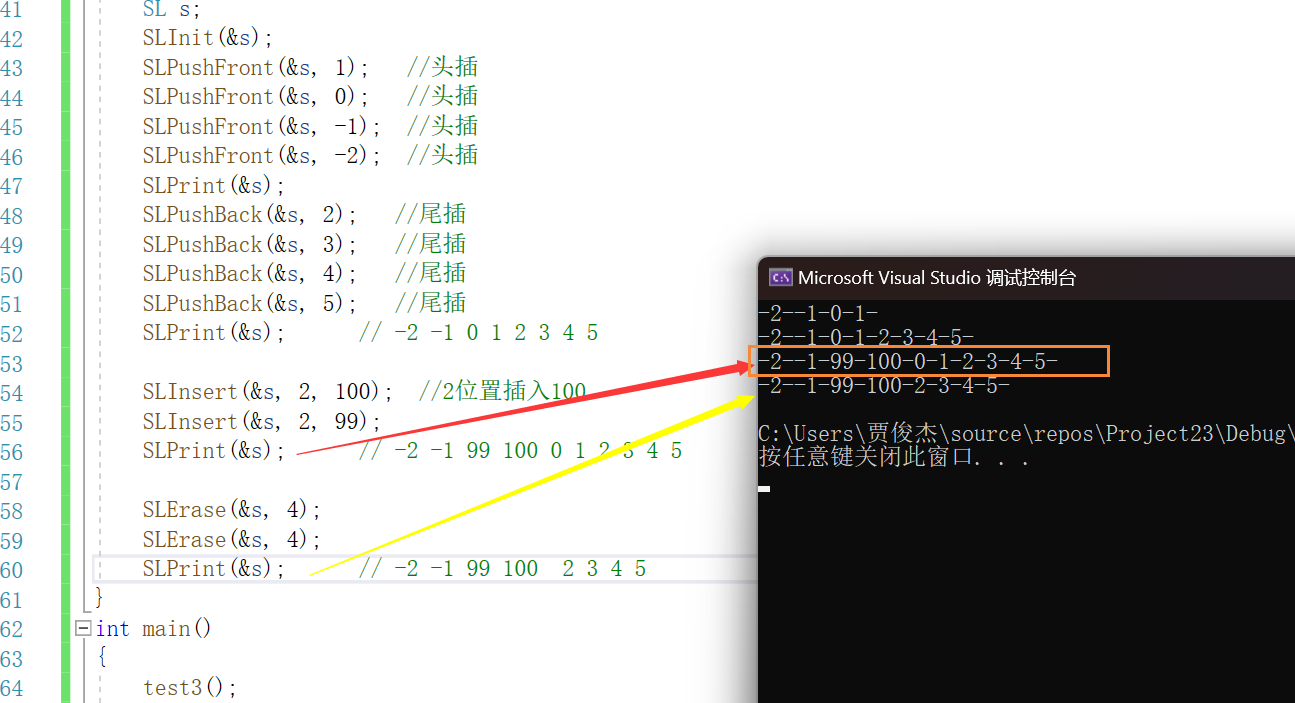
最近学校开始学习数据结构了,没事就手搓一个顺序表。🌈线性表线性表是n个具有相同特性的数据元素的有限序列,是一种实际中广泛使用的数据结构,常见的线性表有顺序表、链表、栈、队列、字符串。线性表在逻辑上是线性结构࿰…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
