设备树信息解析相关函数
一。可以通过三种不同的方式解析设备树节点:
1.根据设备树节点的名字解析设备树节点
struct device_node *of_find_node_by_name(struct device_node *from, const char *name);
参数:
from:当前节点父节点首地址
name:设备树节点名字
返回值:
成功获取到解析的设备树节点信息结构体首地址,失败返回NULL
2.根据设备树节点路径解析设备树节点
struct device_node *of_find_node_by_path(const char *path)
参数:
path:设备树节点路径 /mynode0x12345678
返回值:
成功获取到解析的设备树节点信息结构体首地址,失败返回NULL
3.根据设备树节点中compatibe键来解析设备树节点
struct device_node *of_find_compatible_node(struct device_node *from, const char *type, const char *compat);
参数:
from:填NULL,默认从根节点开始解析
type:NULL
compat:填写要解析的设备树节点中compatible的值
返回值:成功获取到解析的设备树节点信息结构体首地址,失败返回NULL
二、
解析设备树节点属性:
1.基于解析后的设备树节点信息结构体解析指定属性键值对
struct property *of_find_property(const struct device_node *np, const char *name, int *lenp)
参数:
np:设备树节点信息结构体指针
name:指定的键名
lenp:获取到的字节个数
返回值:成功返回属性结构体首地址,失败返回NULL
相关文章:

设备树信息解析相关函数
一。可以通过三种不同的方式解析设备树节点: 1.根据设备树节点的名字解析设备树节点 struct device_node *of_find_node_by_name(struct device_node *from, const char *name); 参数: from:当前节点父节点首地址 name:设备树节点名字 …...

LeetCode-1124. 表现良好的最长时间段【哈希表,前缀和,单调栈】
LeetCode-1124. 表现良好的最长时间段【哈希表,前缀和,单调栈】题目描述:解题思路一:查字典。cur是当前的前缀和(劳累与不劳累天数之差),向前遍历。有两种情况。情况一,若cur大于0则是[0,i]的劳累与不劳累天…...
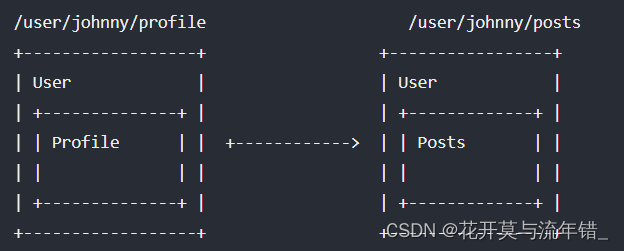
vue-router路由配置
介绍:路由配置主要是用来确定网站访问路径对应哪个文件代码显示的,这里主要描述路由的配置、子路由、动态路由(运行中添加删除路由) 1、npm添加 npm install vue-router // 执行完后会自动在package.json中添加 "vue-router…...

中国计算机设计大赛来啦!用飞桨驱动智慧救援机器狗
中国大学生计算机设计大赛是我国高校面向本科生最早的赛事之一,自2008年开赛至今,一直由教育部高校与计算机相关教指委等或独立或联合主办。大赛的目的是以赛促学、以赛促教、以赛促创,为国家培养德智体美劳全面发展的创新型、复合型、应…...

嘉定区2022年高新技术企业认定资助申报指南
各镇人民政府,街道办事处,嘉定工业区、菊园新区管委会,各相关企业: 为推进实施创新驱动发展战略,加快建设具有全球影响力的科技创新中心,根据《嘉定区关于加快本区高新技术企业发展的实施方案(…...

【C++】关键字、命名空间、输入和输出、缺省参数、函数重载
C关键字(C98)命名空间产生背景命名空间定义命名空间使用输入&输出缺省参数什么叫缺省参数缺省参数分类函数重载函数重载概念C支持函数重载的原理--名字修饰C关键字(C98) C总计63个关键字,C语言32个关键字。 下面我们先看一下C有多少关键字,不对关键…...

【一道面试题】关于HashMap的一系列问题
HashMap底层数据结构在1.7与1.8的变化 1.7是基于数组链表实现的,1.8是基于数组链表红黑树实现的,链表长度达到8时会树化 使用哈希表的好处 使用hash表是为了提升查找效率,比如我现在要在数组中查找一个A对象,在这种情况下是无法…...

论文笔记: Monocular Depth Estimation: a Review of the 2022 State of the Art
中文标题:单目深度估计:回顾2022年最先进技术 本文对比了物种最近的基于深度学习的单目深度估计方法: GPLDepth(2022)[15]: Global-Local Path Networks for Monocular Depth Estimation with Vertical CutDepthAdabins(2021)[1]: Adabins:…...
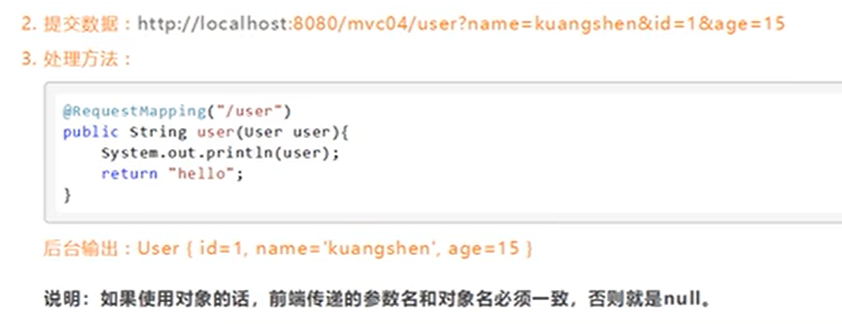
Springmvc补充配置
Controller配置总结 控制器通常通过接口定义或注解定义两种方法实现 在用接口定义写控制器时,需要去Spring配置文件中注册请求的bean;name对应请求路径,class对应处理请求的类。 <bean id"/hello" class"com.demo.Controller.HelloCo…...

MySQL 的 datetime等日期和时间处理SQL函数及格式化显示
MySQL 的 datetime等日期和时间处理SQL函数及格式化显示MySQL 时间相关的SQL函数:MySQL的SQL DATE_FORMAT函数:用于以不同的格式显示日期/时间数据。DATE_FORMAT(date, format) 根据格式串 format 格式化日期或日期和时间值 date,返回结果串。…...

基于微信云开发的防诈反诈宣传教育答题小程序
基于微信云开发的防诈反诈宣传教育答题小程序一、前言介绍作为当代大学生,诈骗事件的发生屡见不鲜,但却未能引起大家的重视。高校以线上宣传、阵地展示为主,线下学习、实地送法为辅,从而构筑立体化反诈骗防线。在线答题考试是一种…...
Map和Set
Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例化子类有关。数据的一般查找方式有两种:直接遍历和二分查找。但这两种查找方式都有很大的局限性,也不便于对数据进行增删查改等操作。对于这一类数据的查找&…...
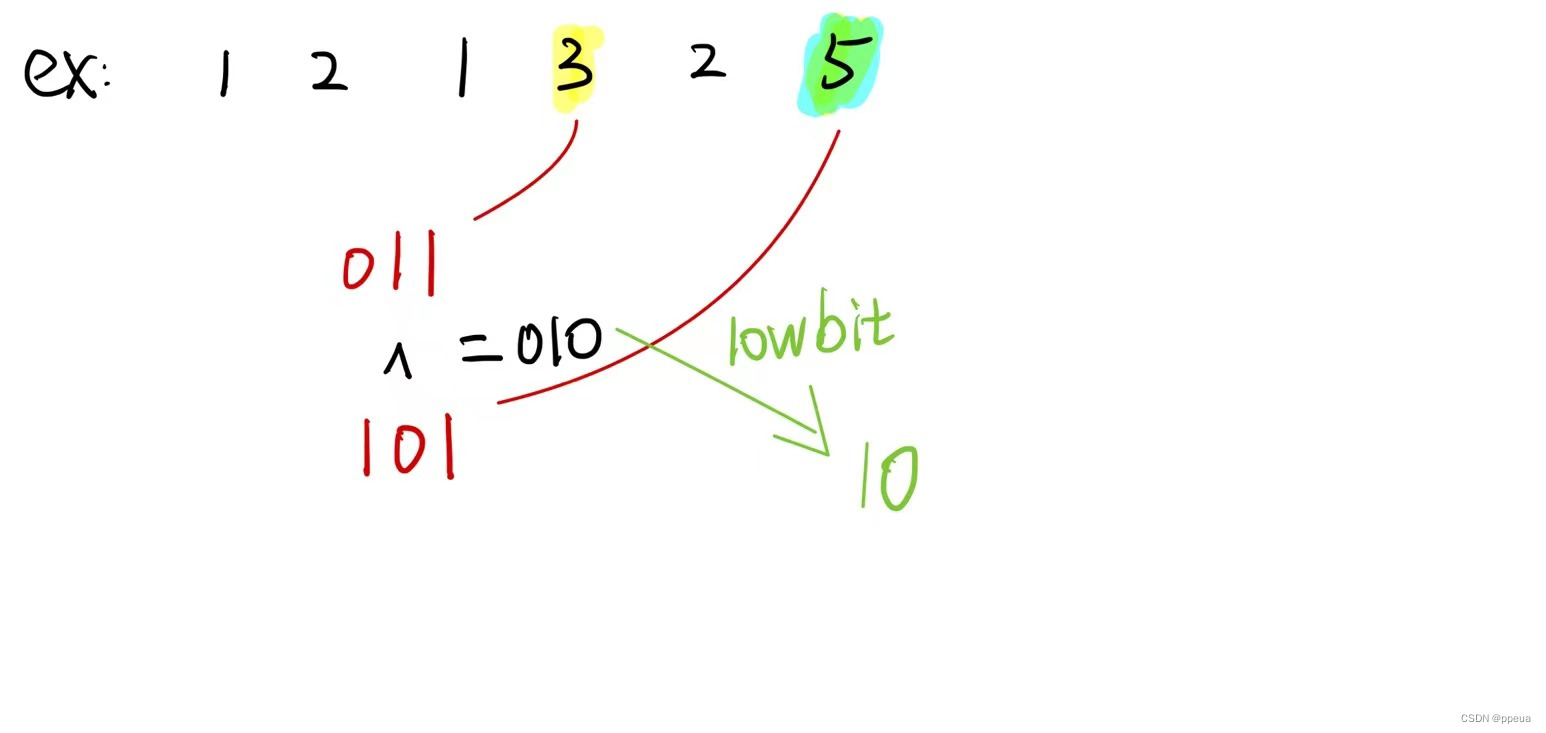
【位运算问题】Leetcode 136、137、260问题详解及代码实现
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

同花顺2023届春招内推
同花顺2023届春招开始啦! 同花顺是国内首家上市的互联网金融信息服务平台,如果你对互联网金融感兴趣,如果你有志向在人工智能方向发挥所长,如果你也是一个激情澎湃的小伙伴,欢迎加入我们!岗位类别…...
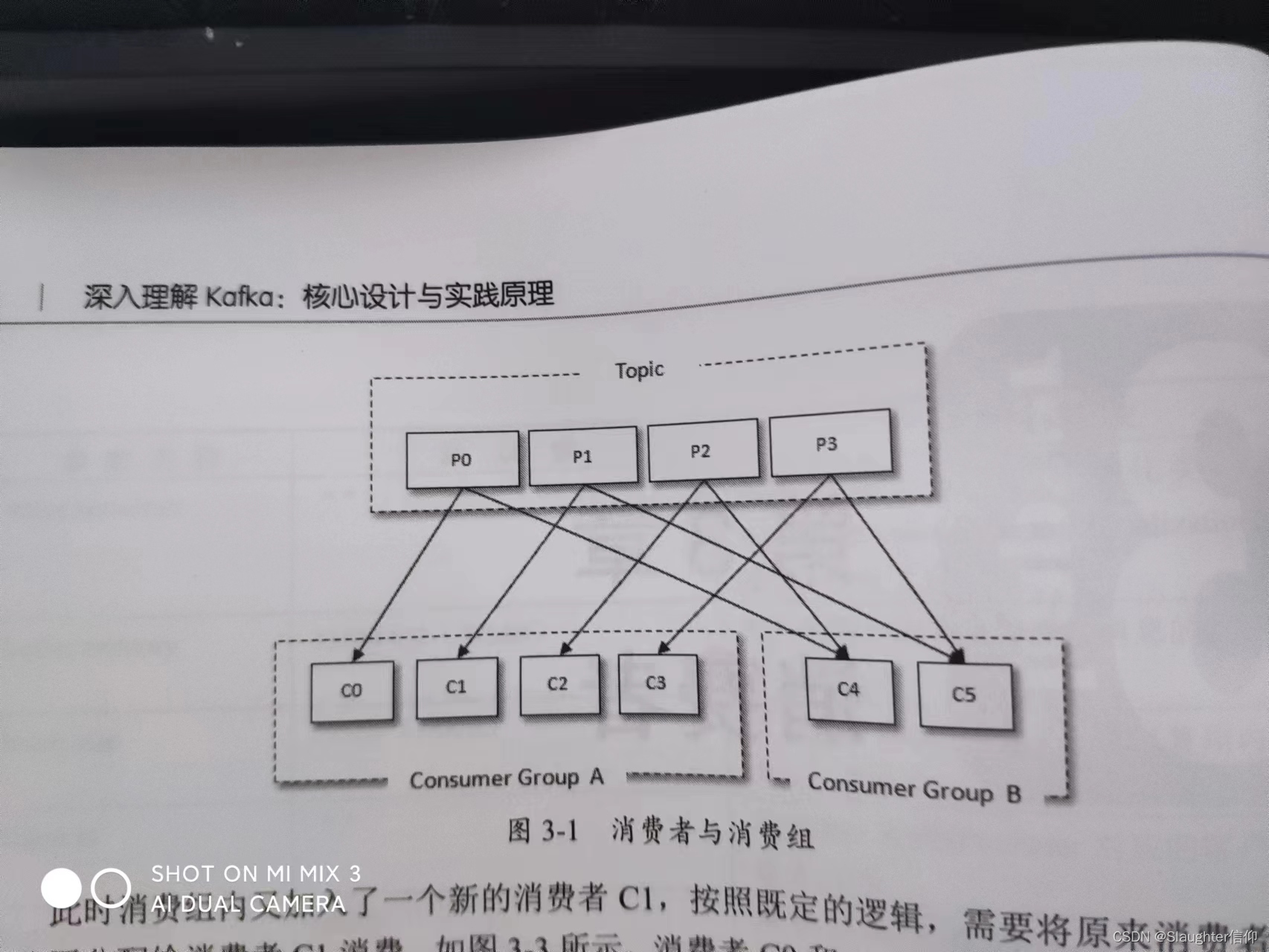
深入Kafka核心设计与实践原理读书笔记第三章消费者
消费者 消费者与消费组 消费者Consumer负责定于kafka中的主题Topic,并且从订阅的主题上拉取消息。与其他消息中间件不同的在于它有一个消费组。每个消费者对应一个消费组,当消息发布到主题后,只会被投递给订阅它的消费组的一个消费者。 如…...

IDEA 中使用 Git 图文教程详解
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

【Linux系统】进程概念
目录 1 冯诺依曼体系结构 2 操作系统(Operator System) 概念 设计OS的目的 定位 总结 系统调用和库函数概念 3 进程 3.1 基本概念 3.2 描述进程-PCB 3.2 组织进程 3.3 查看进程 3.4 通过系统调用获取进程标示符 3.5 进程状态 在了解进程概念前我们还得了解下冯诺…...
)
上课睡觉(2023寒假每日一题 4)
有 NNN 堆石子,每堆的石子数量分别为 a1,a2,…,aNa_1,a_2,…,a_Na1,a2,…,aN。 你可以对石子堆进行合并操作,将两个相邻的石子堆合并为一个石子堆,例如,如果 a[1,2,3,4,5]a[1,2,3,4,5]a[1,2,3,4,5],合并第 2,32…...

【Selenium学习】Selenium 中常用的基本方法
1.send_keys 方法模拟键盘键入此方法类似于模拟键盘键入。以在百度首页搜索框输入“Selenium”为例,代码如下:# _*_ coding:utf-8 _*_ """ name:zhangxingzai date:2023/2/13 form:《Selenium 3Python 3自动化测试项目实战》 …...
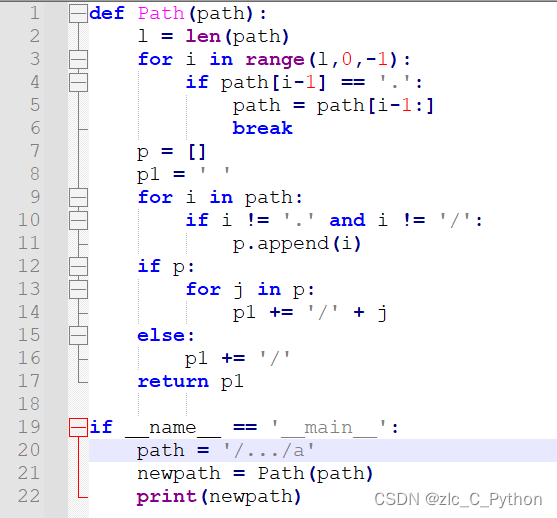
python练习——简化路径
项目场景: 给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 /开头),请你将其转化为更加简洁的规范路径。在 Unix 风格的文件系统中,一个点(.)表示当前目录本…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
