12- 降维算法 (PCA降维/LDA分类/NMF) (数据处理)
- 数据降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。
- PCA算法有两种实现方法:
- 基于特征值分解协方差矩阵实现PCA算法
- 基于SVD分解协方差矩阵实现PCA算法
from sklearn.decomposition import PCApca = PCA(n_components= 2)X_pca = pca.fit_transform(X)- LDA线性判别分析也是一种经典的降维方法,LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
- NMF非负矩阵分解: NMF的基本思想可以简单描述为:对于任意给定的一个非负矩阵A,NMF算法能够寻找到一个非负矩阵U和一个非负矩阵V,使得满足 ,从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。
from sklearn.decomposition import NMF
nmf = NMF(n_components=2,init = 'nndsvda',max_iter=1000)
# 降维之后的数据
W = nmf.fit_transform(X)-
LLE局部线性嵌入降维算法: 在处理所谓流形降维的时候,效果比PCA要好很多。首先,所谓流形,我们脑海里最直观的印象就是Swiss roll,在吃它的时候喜欢把它整个摊开成一张饼再吃,其实这个过程就实现了对瑞士卷的降维操作,即从三维降到了两维。
from sklearn.manifold import LocallyLinearEmbeddinglle = LocallyLinearEmbedding(n_neighbors=10,n_components=2)lle.fit(X)数据降维简介: 降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。
降维算法优点
- 减少所需的存储空间。
- 加快计算速度(例如在机器学习算法中),更少的维数意味着更少的计算,并且更少的维数可以允许使用不适合大量维数的算法。
- 去除冗余特征,例如在以平方米和平方公里在存储地形尺寸方面,两者一起用没有意义(数据收集有缺陷)。
- 将数据的维数降低到2D或3D可以允许我们绘制和可视化它,可能观察模式,给我们提供直观感受。
- 太多的特征或太复杂的模型可以导致过拟合。
- 较简单的模型在小数据集上有更强的鲁棒性。
一 降维算法适用性
在许多领域的研究与应用中,通常需要对含有多个变量的数据进行观测,收集大量数据后进行分析研究寻找规律。多变量大数据集无疑会为研究和应用提供丰富的信息,但是也在一定程度上增加了数据采集的工作量。更重要的是在很多情形下,多变量之间可能存在相关性,从而增加了问题分析的复杂性。如果分别对每个指标进行分析,分析往往是孤立的,不能完全利用数据中的信息,因此盲目减少指标会损失很多有用的信息,从而产生错误的结论。
因此需要找到一种合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。
二 数据降维方法
主要的方法是线性映射和非线性映射方法两大类。
- 线性映射方法的代表方法有:PCA(Principal Component Analysis),LDA(Discriminant Analysis)。
- 非线性映射方法的代表方法有:核方法(KernelPCA)、流形学习(ISOMap,LLE)。
- 非负矩阵分解(NMF)是在矩阵中所有元素均为非负数的约束条件之下的矩阵分解方法 。
三 PCA降维
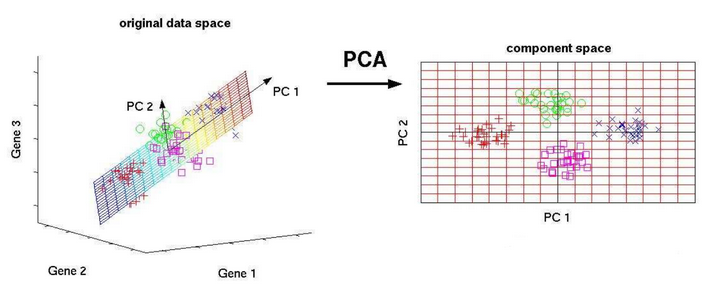
- PCA(Principal Components Analysis)即主成分分析,是一种图像处理中使用最广泛的数据降维算法。它不仅仅是对高维数据进行降维,更重要的是经过降维去除了噪声,发现了数据中的模式。PCA把原先的n个特征用数目更少的m个特征取代,新特征是旧特征的线性组合,这些线性组合最大化样本方差,尽量使新的m个特征互不相关。
- PCA方法通过消除数据的相关性,找到一个空间,使得各个类别的数据在该空间上能够很好地分离。在下图中,有一些离散的二维分布点,其中棕色表示一类集合,黄色表示另一类集合,假设这两个类别可以用特征X和特征Y进行描述,由图可知,在X轴和Y轴上这两个类别的投影是重叠的,表明这些点的两个特征X和Y没有表现出突出的识别性。但是两个类的投影在Z轴上区分度较大,显示出很好的识别性。PCA就是这样的一个工具,它可以产生非常好的降维效果。
- PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。

通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中,实现数据特征的降维。
由于得到协方差矩阵的特征值特征向量有两种方法:特征值分解协方差矩阵、奇异值分解协方差矩阵,所以PCA算法有两种实现方法:基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。
四 PCA降维原理
4.1. 协方差和散度矩阵
样本均值:
样本方差:
样本X和样本Y的协方差:
由上面的公式,我们可以得到以下结论:
-
方差的计算公式是针对一维特征,即针对同一特征不同样本的取值来进行计算得到;而协方差则必须要求至少满足二维特征;方差是协方差的特殊情况。
-
方差和协方差的除数是n-1,这是为了得到方差和协方差的无偏估计。
-
协方差为正时,说明X和Y是正相关关系;协方差为负时,说明X和Y是负相关关系;协方差为0时,说明X和Y是相互独立。Cov(X,X)就是X的方差。
-
当样本是n维数据时,它们的协方差实际上是协方差矩阵(对称方阵)。如: 对于3维数据(x,y,z)。
-
对于数据X的散度矩阵为Scatter matrix。其实协方差矩阵和散度矩阵关系密切,散度矩阵就是协方差矩阵乘以(总数据量n-1)。因此它们的特征值和特征向量是一样的。这里值得注意的是,散度矩阵是SVD奇异值分解的一步,因此PCA和SVD是有很大联系。
import numpy as np
A = np.random.randint(0,10,size = (3,3))
# 协方差
cov = np.cov(A,rowvar=True)
# 散度矩阵
B = (A - A.mean(axis = 1).reshape(-1,1))
scatter = B.dot(B.T)
display(A,cov,scatter)4.2.特征值分解矩阵原理
-
特征值与特征向量:
其中,λ是特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量
-
特征值分解矩阵,对于矩阵A,有一组特征向量v,将这组向量进行正交化单位化,就能得到一组正交单位向量。特征值分解,就是将矩阵A分解为如下式:
-
其中,P是矩阵A的特征向量组成的矩阵,则是一个对角阵,对角线上的元素就是特征值。
五 SVD分解矩阵原理
是一种因子分解运算,将一个矩阵分解为3个矩阵的乘积
-
3个矩阵: U, Σ 和 V,其中U和V是正交矩阵,分别称为左奇异值、右奇异值,Σ 为奇异值
-
奇异值分解是一个能适用于任意矩阵的一种分解的方法,对于任意矩阵A总是存在一个奇异值分解:
-
full_matrices =True 时,表示U和V是全矩阵
假设A是一个
的矩阵,那么得到的U是一个
的方阵,U里面的正交向量被称为左奇异向量。Σ是一个
的矩阵,Σ除了对角线其它元素都为0,对角线上的元素称为奇异值。v的转置矩阵,是一个
的矩阵,它里面的正交向量被称为右奇异值向量。而且一般来讲,我们会将Σ上的值按从大到小的顺序排列。
-
full_matrices=False 时,表示U和V不是全矩阵
假设A是一个
的矩阵,那么得到的U是一个
的方阵,U里面的正交向量被称为左奇异向量。Σ是一个
的矩阵,Σ除了对角线其它元素都为0,对角线上的元素称为奇异值。v的转置矩阵,是一个
的矩阵,它里面的正交向量被称为右奇异值向量。而且一般来讲,我们会将Σ上的值按从大到小的顺序排列。
-
六 PCA算法两种实现方式
6.1.基于特征值分解协方差矩阵实现PCA算法
-
去平均值(即去中心化),即每一位特征减去各自的平均值
-
计算协方差矩阵
-
用特征值分解方法求协方差矩阵的特征值与特征向量
-
对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵ev
-
将数据转换到k个特征向量构建的新空间中,即 X_pca=
# 1、去中心化
# B = X - X.mean(axis = 0)
# B[:5]# 2、协方差
# 方差是协方差特殊形式
# 协方差矩阵
V = np.cov(B,rowvar=False,bias = True)# 3、协方差矩阵的特征值和特征向量
# 特征值和特征向量矩阵的概念
eigen,ev = np.linalg.eig(V)
display(eigen,ev)# 4、降维标准,2个特征,选取两个最大的特征值所对应的特征的特征向量
# 百分比,计算各特征值,占权重,累加可以
cond = (eigen/eigen.sum()).cumsum() >= 0.98
index = cond.argmax()
ev = ev[:,:index + 1]# 5、进行矩阵运算
pca_result = B.dot(ev)# 6、标准化
pca_result = (pca_result -pca_result.mean(axis = 0))/pca_result.std(axis = 0)
pca_result[:5]6.2.基于SVD分解协方差矩阵实现PCA算法
-
去平均值 (即去中心化),即每一位特征减去各自的平均值
-
通过SVD对第一步结果进行奇异值分解
-
特征值默认从大到小排列,选择k个作为降维特征,对左奇异值矩阵进行切片即可(U[:,:k])
-
归一化处理(无偏差、偏差)
-
无偏估计
-
总体标准差
-
样本标准差
from scipy import linalg
from sklearn import datasetsn_components_ = 3
X,y = datasets.load_iris(return_X_y = True)# 1、去中心化
mean_ = np.mean(X, axis=0)
X -= mean_# 2、奇异值分解
U, S, Vt = linalg.svd(X, full_matrices=False)# 3、符号翻转(如果为负数,那么变成正直)
max_abs_cols = np.argmax(np.abs(U), axis=0)
signs = np.sign(U[max_abs_cols, range(U.shape[1])])
U *= signs# 4、降维特征筛选
U = U[:, :n_components_]# 5、归一化
# U = (U - U.mean(axis = 0))/U.std(axis = 0)
U *= np.sqrt(X.shape[0] - 1)
U[:5]七 LDA线性判别
LDA线性判别分析也是一种经典的降维方法,LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
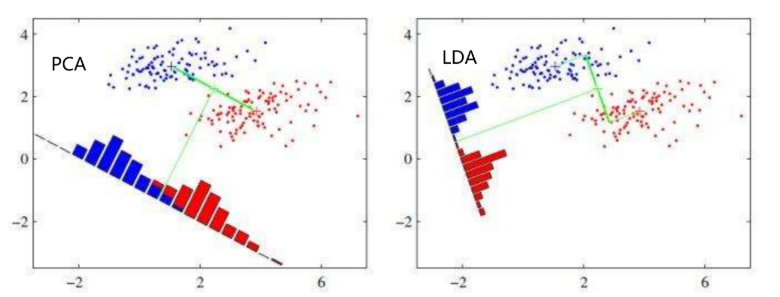
给定训练集样例,设法将样例投影到一条直线上,使得同类样例的投影尽可能接近,异类样例的投影点尽可能原理;在对新的样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。
LDA算法实现方式:
-
计算数据总的散度矩阵
-
计算数据类内散度矩阵
-
计算类间散度矩阵
-
特征值和特征向量计算
-
筛选特征向量,进行矩阵运算返回输出结果
import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn import datasets
# scipy这个模块下的线性代数子模块
from scipy import linalg# 加载数据
X,y = datasets.load_iris(return_X_y=True)# 1、总的散度矩阵
# 协方差
St = np.cov(X.T,bias = 1)# 2、类内的散度矩阵
# Scatter散点图,within(内)
Sw = np.full(shape = (4,4),fill_value=0,dtype=np.float64)
for i in range(3):Sw += np.cov(X[y == i],rowvar = False,bias = 1)
Sw/=3# 3、计算类间的散度矩阵
# Scatter between
Sb = St - Sw# 4、特征值,和特征向量
eigen,ev = linalg.eigh(Sb,Sw)
ev = ev[:, np.argsort(eigen)[::-1]][:,:2]# 5、删选特征向量,进行矩阵运算
X.dot(ev)[:5]八 NMF非负矩阵分解
NMF的基本思想可以简单描述为:对于任意给定的一个非负矩阵A,NMF算法能够寻找到一个非负矩阵U和一个非负矩阵V,使得满足 ,从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。
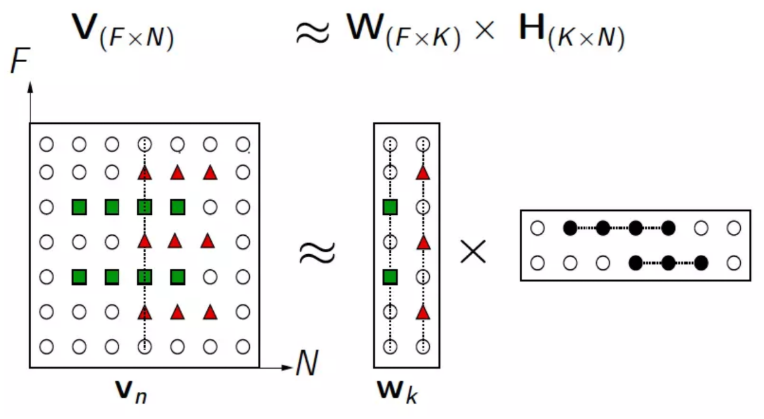
解前后可理解为:原始矩阵V的列向量是对左矩阵W中所有列向量的加权和,而权重系数就是右矩阵对应列向量的元素,故称W为基矩阵,H为系数矩阵。
原矩阵V中的一列向量可以解释为对左矩阵W中所有列向量(称为基向量)的加权和,而权重系数为右矩阵H中对应列向量中的元素。这种基于基向量组合的表示形式具有很直观的语义解释,它反映了人类思维中“局部构成整体”的概念。
虽然NMF是一个很厉害的算法,但其实质是加权和,我们可以在原理上等效为基本的线性方程。
import numpy as np
from sklearn import datasets
from sklearn.decomposition import NMF# 加载数据
X,y = datasets.load_iris(return_X_y=True)# 声明算法
nmf = NMF(n_components=2,init = 'nndsvda',max_iter=1000)# 降维之后的数据
W = nmf.fit_transform(X)
display(W[:5])# NMF另一半矩阵H
H = nmf.components_# X ≈ W • H九 LLE局部线性嵌入降维算法
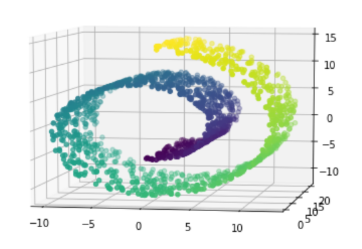
所谓LLE(局部线性嵌入)即”Locally Linear Embedding”的降维算法,在处理所谓流形降维的时候,效果比PCA要好很多。首先,所谓流形,我们脑海里最直观的印象就是Swiss roll,在吃它的时候喜欢把它整个摊开成一张饼再吃,其实这个过程就实现了对瑞士卷的降维操作,即从三维降到了两维。降维前,我们看到相邻的卷层之间看着距离很近,但其实摊开成饼状后才发现其实距离很远,所以如果不进行降维操作,而是直接根据近邻原则去判断相似性其实是不准确的。
和传统的PCA,LDA等关注样本方差的降维方法相比,LLE关注于降维时保持样本局部的线性特征(保持原有拓扑结构),由于LLE在降维时保持了样本的局部特征,它广泛的用于图像识别,高维数据可视化等领域。LLE是非线性降维技术,可以说是流形学习方法最经典的算法之一。很多后续的流形学习、降维方法都与LLE有密切联系。
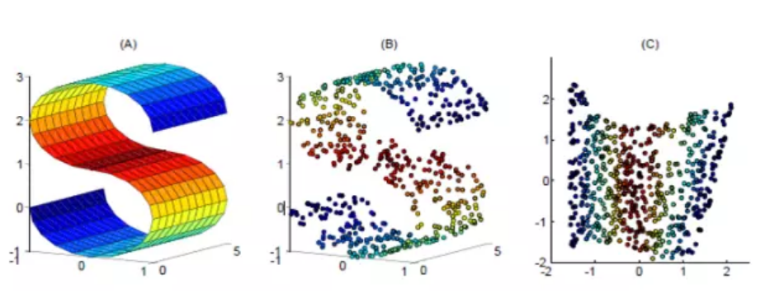
LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到,LLE算法主要步骤:
-
寻找每个样本点的k个近邻点;
-
由每个样本点的近邻点计算出该样本点的局部重建权值矩阵;
-
由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。
# 降维,高维数据降成低维的数据# manifold 流形from sklearn.manifold import LocallyLinearEmbeddingfrom sklearn.decomposition import PCAfrom sklearn import datasetsimport matplotlib.pyplot as plt%matplotlib inlinefrom mpl_toolkits.mplot3d.axes3d import Axes3DX,t = datasets.make_swiss_roll(n_samples=1500,noise=0.05,random_state= 1024)fig = plt.figure(figsize=(12,9))# axes3D = Axes3D(fig)axes3D = fig.add_subplot(projection = '3d')axes3D.view_init(7,-80)axes3D.scatter(X[:,0],X[:,1],X[:,2],c = t)pca = PCA(n_components= 2)X_pca = pca.fit_transform(X)plt.scatter(X_pca[:,0],X_pca[:,1],c = t)lle = LocallyLinearEmbedding(n_neighbors=10,n_components=2)lle.fit(X)X_lle = lle.transform(X)plt.scatter(X_lle[:,0],X_lle[:,1],c = t)
相关文章:

12- 降维算法 (PCA降维/LDA分类/NMF) (数据处理)
数据降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。PCA算法有两种实现方法: 基于特征值分解协方差矩阵实现PCA算法基于SVD分解协方差矩阵实…...

QT+ OpenGL学习
文章目录QT OpenGLQOpenGLWidget:不需要GLFWQOpenGLFunction_X_X_Core:不需要GLAD你好,三角形顶点输入顶点着色器片段着色器链接着色器本节代码元素缓冲对象EBOQT交互GLSLGLSL支持的类型输入输出Uniform纹理纹理单元纹理环绕纹理过滤多级渐远纹理QT OpenGL 本篇完整…...

C语言(字符串输入)
目录 一.gets和puts组合 二.fgets()和fputs() 三.fgets()函数返回 四.fgets读取满问题 五.修改fgets函数,自动用\0替换\n 一.gets和puts组合 Gets()读取整行输入,知道遇到换行符,然后丢弃换行符,存储其余字符,并在这些字符的…...
(JAVA))
背包问题求方案数(AcWing)(JAVA)
有 N件物品和一个容量是 V 的背包。每件物品只能使用一次。 第 i 件物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出 最优选法的方案数。注意答案可能很大,请输出答…...
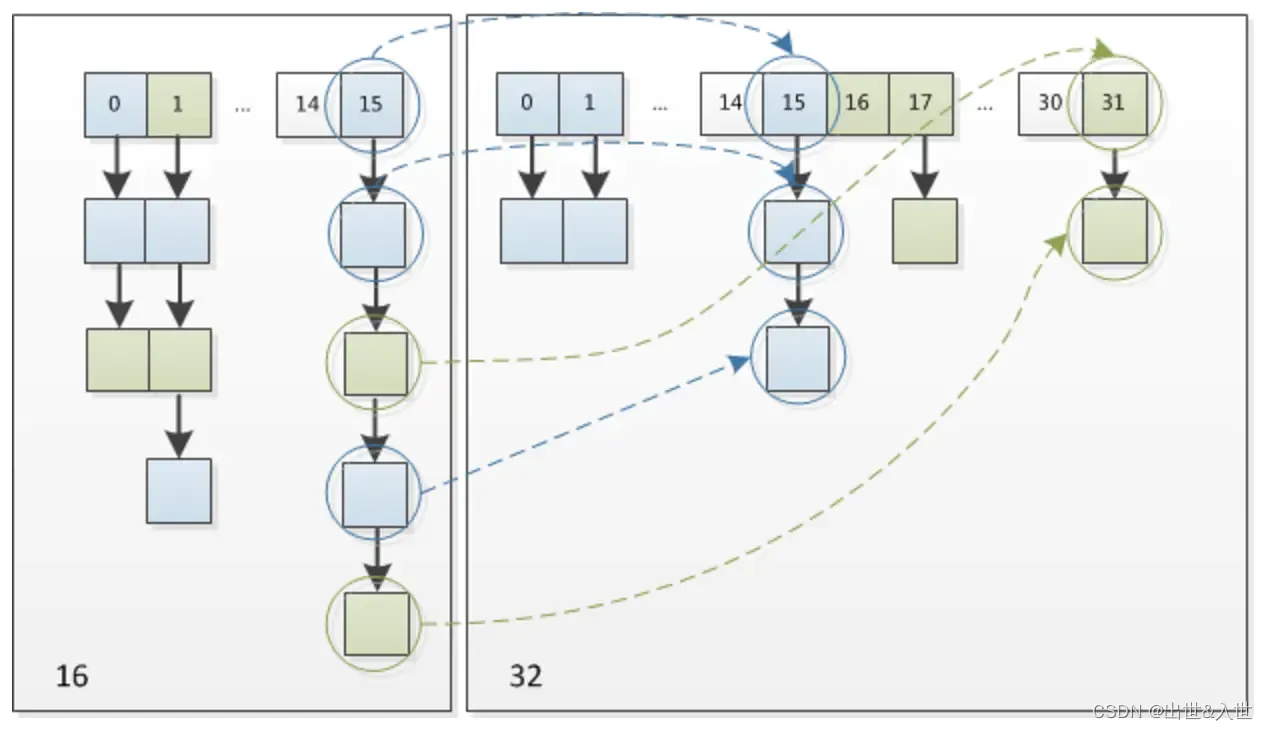
一篇文章带你读懂HashMap
HashMap是面试中经常问到的一个知识点,也是判断一个候选人基础是否扎实的标准之一。可见HashMap的掌握是多重要。 一、HashMap源码分析 1、构造函数 让我们先从构造函数说起,HashMap有四个构造方法,别慌 1.1 HashMap() // 1.无参构造方法、// 构造一…...

Java如何进行优雅的判空——Optional类的灵活应用
0 引言 在Java Web项目开发中,经常令人头疼的NPE问题(NullPointerException)——空指针,例如我们在调用equal()方法时,就经常会出现NPE问题: String str null; str.equals("fsfs");…...

Fluent Python 笔记 第 12 章 继承的优缺点
重点是说明对 Python 而言尤为重要的两个细节: 子类化内置类型的缺点多重继承和方法解析顺序 12.1 子类化内置类型很麻烦 内置类型(使用 C 语言编写)不会调用用户定义的类覆盖的特殊方法。 不要子类化内置类型,用户自己定义的类应 该继承 collections 模块(http…...

Go语言读取解析yml文件,快速转换yml到go struct
YAML (YAML Aint a Markup Language)是一种标记语言,通常以.yml为后缀的文件,是一种直观的能够被计算机程序识别的数据序列化格式,并且容易被人类阅读,容易和脚本语言交互的,可以被支持YAML库的不同的编程语言程序导入…...
)
第二十六章 java并发常见知识内容(ThreadLocal 详解)
JAVA重要知识点带着疑问看ThreadLocalGC 之后 key 是否为 null?ThreadLocalMap Hash 算法ThreadLocalMap Hash 冲突ThreadLocalMap.set()方法ThreadLocalMap过期 key 的探测式清理流程ThreadLocalMap扩容机制ThreadLocalMap.get()详解ThreadLocalMap过期 key 的启发…...

人类的第一语言是什么
其实机器智能始终存在一个争议 没有人类的肢体和感受器无法理解和感同身受 这不用想是自然,但是可以通过虚拟数据进行模拟,深度学习便是 深度学习是模拟简单输入输出的最好选择,但不是开放性的学习 没有智能交互的智能永远不是智能 就像狼孩一…...

jsp(全部知识点)
👌 棒棒有言:也许我一直照着别人的方向飞,可是这次,我想要用我的方式飞翔一次!人生,既要淡,又要有味。凡事不必太在意,一切随缘,缘深多聚聚,缘浅随它去。凡事…...

测试开发面试基础题
1.对测试开发的理解 测试开发首先离不开测试,而软件测试是指,在规定的条件下对程序进行操作,以发现程序错误,衡量软件质量,并对其是否能满足设计要求进行评估的过程。 而且,现在不仅仅是通过手工测试来发…...
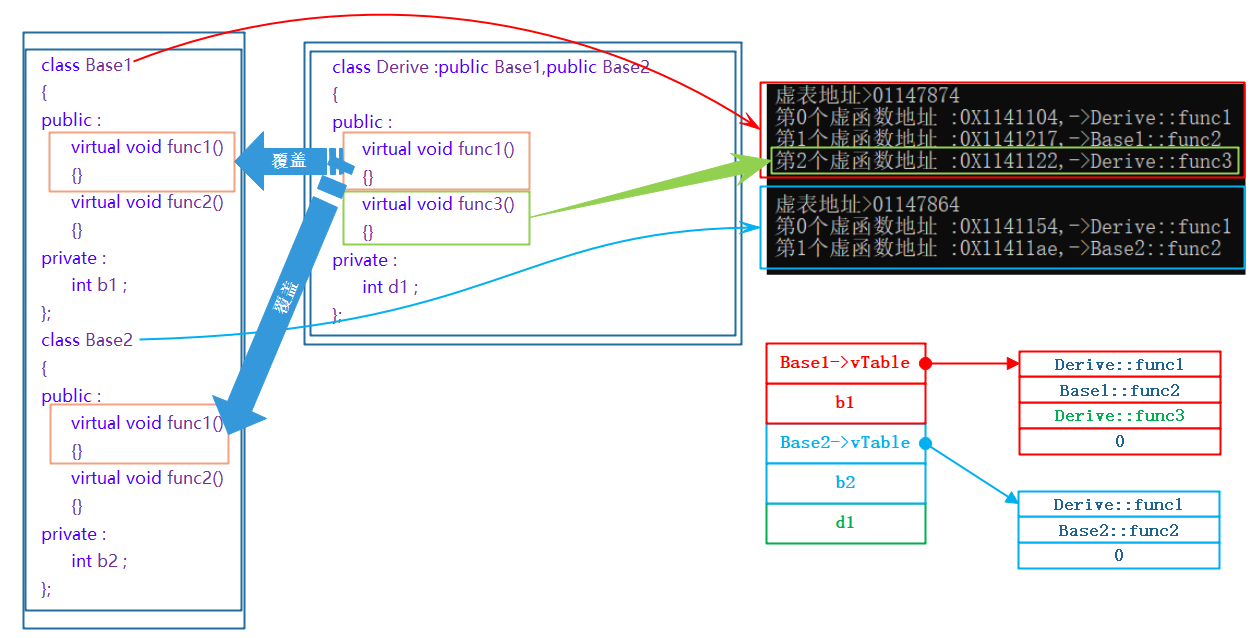
C++——多态|虚函数|重写|虚表
文章目录1. 多态的概念1.1 概念2. 多态的定义及实现2.1多态的构成条件2.2 虚函数2.3虚函数的重写虚函数重写的三个例外:2.4 普通调用和多态调用:2.5 C11 override 和 final2.6 重载、虚函数的覆盖(重写)、隐藏(重定义)的对比3. 抽象类(有关纯虚函数)3.1 …...

IPV4地址详解
文章目录IPV4地址分类编址划分子网无分类编制CIDR路由聚合应用规划(子网划分的细节)定长的子网掩码FLSM变长的子网掩码VLSMIPV4地址 IPV4地址就是给因特网(Internet)上的每一台主机(或路由器)的每一个接口…...
(一)初识Streamlit(附安装)
本入门指南介绍Streamlit的工作原理、如何在您首选的操作系统上安装Streamlit,以及如何创建第一个Streamlit应用程序! 1 安装 1.1 先决条件 Python 3.7 – Python 3.11 **注:我这里使用的是anaconda的虚拟环境,用pycharm编写代…...
| 刷完获取OD招聘渠道)
【新】华为OD机试 - 斗地主 2(Python)| 刷完获取OD招聘渠道
斗地主 2 题目描述 在斗地主扑克牌游戏中,扑克牌由小到大的顺序为3 4 5 6 7 8 9 10 J Q K A 2 玩家可以出的扑克牌阵型有,单张,对子,顺子,飞机,炸弹等 其中顺子的出牌规则为,由至少 5 张由小到大连续递增的扑克牌组成 且不能包含2 例如:{3,4,5,6,7}、{3,4,5,6,7,8,9,1…...
秒杀项目之消息推送
目录一、创建消费者二、创建订单链路配置2.1 定义RabbitMQ配置类2.2 创建RabbitmqOrderConfig配置类三、如何实现RabbitMQ重复投递机制3.1 开启发送者消息确认模式3.2 消费发送确认3.2.1 创建ConfirmCallBack确认模式3.2.2 创建ReturnCallBack退回模式3.3 创建生产者3.4 创建消…...
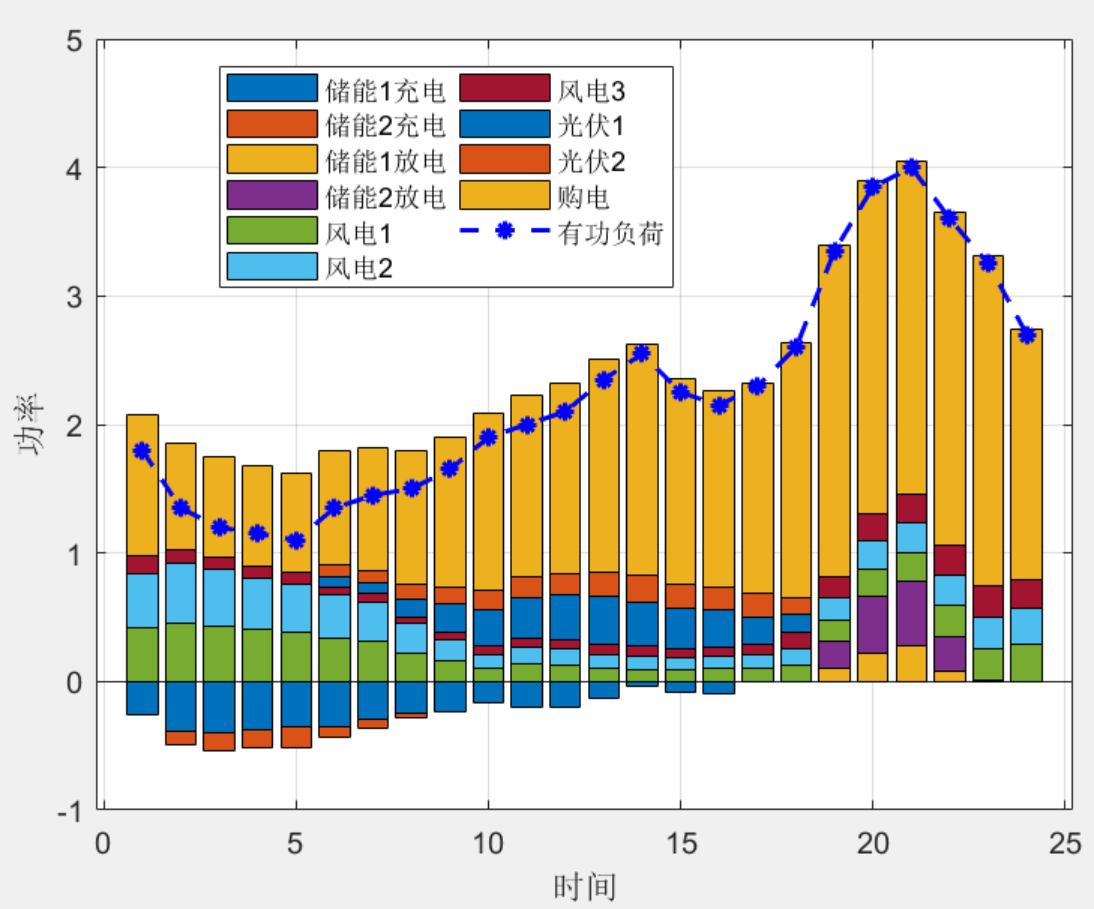
【重磅】IEEE33配电网两阶段鲁棒优化调度CCG
目录 1 前言 2基本内容 2.1 配网两阶段鲁棒模型 2.2 求解步骤 3部分程序 4程序结果 5程序链接 1 前言 鲁棒优化是电力系统研究的热点,而两阶段鲁棒和分布鲁棒研究就成为各类期刊(sci/ei/核心)的宠儿,最简单的思路是通过改…...

GPT2代码拆解+生成实例
本文代码来自博客,GPT2模型解析参考 import torch import copy import torch.nn as nn import torch.nn.functional as F from torch.nn.modules import ModuleList from torch.nn.modules.normalization import LayerNorm import numpy as np import os from tqd…...

基于android的即时通讯APP 聊天APP
基于android的即时通讯APP 或者 聊天APP 一 项目概述 该项目是基于Android 的聊天APP系统,该APP包含前台,后台管理系统,前台包含用户通讯录,用户详情,用户聊天服务,用户二维码,发现功能,发现详情 , 个人中心, 个人信…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
