CF1707E Replace
题目描述
给定一个长为 nnn 的序列 a1,…,ana_1,\ldots,a_na1,…,an,其中对于任意的 iii 满足 1≤ai≤n1 \leq a_i \leq n1≤ai≤n。
定义一个二元组函数如下:
f((l,r))=(min{al,…,ar},max{al,…,ar})(l≤r)f((l,r))=(\min\{a_l,\ldots,a_r\},\max\{a_l,\ldots,a_r\})(l \leq r)f((l,r))=(min{al,…,ar},max{al,…,ar})(l≤r)
你需要回答 qqq 次询问,每次给定 (li,ri)(l_i,r_i)(li,ri),问其最少经过多少次 fff 的调用(即 (l,r)→f((l,r))(l,r) \rightarrow f((l,r))(l,r)→f((l,r)))使得 (li,ri)(l_i,r_i)(li,ri) 变成 (1,n)(1,n)(1,n),若无解请输出 -1。
题解
智慧的性质题
首先注意到f((l,r))=⋃i=lr−1f((i,i+1))f((l,r))=\bigcup_{i=l}^{r-1}f((i,i+1))f((l,r))=⋃i=lr−1f((i,i+1))
发现可以推广到fk((l,r))=⋃i=lr−1fk((i,i+1))f^k((l,r))=\bigcup_{i=l}^{r-1}f^k((i,i+1))fk((l,r))=⋃i=lr−1fk((i,i+1)),可以用归纳法证明
接下来的做法就容易可以想出了
设Fi,j=f2i((j,j+1))F_{i,j}=f^{2^i}((j,j+1))Fi,j=f2i((j,j+1)),然后倍增解决,合并区间可以用线段树,长度为111的线段需要特别处理
code\text{code}code
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
void read(int &res)
{res=0;char ch=getchar();while(ch<'0'||ch>'9') ch=getchar();while('0'<=ch&&ch<='9') res=(res<<1)+(res<<3)+(ch^48),ch=getchar();
}
const int N=1e5+100,B=40;
int n,q,a[N+10];
struct seg
{int l,r;
}f[B+10][N+10];
int g[B+10][N+10];
seg merge(seg a,seg b){return (seg){min(a.l,b.l),max(a.r,b.r)};}
struct SEG
{seg t[N<<2|1];#define ls (p<<1)#define rs (p<<1|1)#define mid ((l+r)>>1)void build(seg *f,int p=1,int l=1,int r=n-1){if(l==r){t[p]=f[l];return;}build(f,ls,l,mid),build(f,rs,mid+1,r);t[p]=merge(t[ls],t[rs]);}seg query(int L,int R,int p=1,int l=1,int r=n-1){if(L<=l&&r<=R) return t[p];if(R<=mid) return query(L,R,ls,l,mid);else if(L>mid) return query(L,R,rs,mid+1,r);else return merge(query(L,R,ls,l,mid),query(L,R,rs,mid+1,r));}#undef ls#undef rs#undef mid
}t[B+10];
int main()
{
// freopen("a.in","r",stdin);read(n),read(q);if(n==1){for(;q--;) printf("0\n");return 0;}for(int i=1;i<=n;i++) read(a[i]);for(int i=1;i<n;i++) f[0][i]=(seg){min(a[i],a[i+1]),max(a[i],a[i+1])},g[0][i]=a[i];t[0].build(f[0]);for(int j=1;j<=B;j++){for(int i=1;i<n;i++){if(f[j-1][i].l==f[j-1][i].r) f[j][i]=(seg){g[j-1][f[j-1][i].l],g[j-1][f[j-1][i].l]};else f[j][i]=t[j-1].query(f[j-1][i].l,f[j-1][i].r-1);}t[j].build(f[j]);for(int i=1;i<=n;i++) g[j][i]=g[j-1][g[j-1][i]];}for(int l,r;q--;){read(l),read(r);if(l==1&&r==n){printf("0\n");continue;}ll ans=0;if(l!=r)for(int i=B;i>=0;i--){seg tmp=t[i].query(l,r-1);if(tmp.l!=1||tmp.r!=n){l=tmp.l,r=tmp.r;ans+=(1ll<<i);}if(l==r) break;}if(l==r) printf("-1\n");else{seg tmp=t[0].query(l,r-1);if(tmp.l==1&&tmp.r==n) printf("%lld\n",ans+1);else printf("-1\n");}}return 0;
}
相关文章:

CF1707E Replace
题目描述 给定一个长为 nnn 的序列 a1,…,ana_1,\ldots,a_na1,…,an,其中对于任意的 iii 满足 1≤ai≤n1 \leq a_i \leq n1≤ai≤n。 定义一个二元组函数如下: f((l,r))(min{al,…,ar},max{al,…,ar})(l≤r)f((l,r))(\min\{a_l,\ldots,a_r\}…...
【Hello Linux】Linux工具介绍 (make/makefile git)
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:介绍Linux的常用工具make/makefile git Linux项目自动化构建工具 – make/Makefile 背景 会不会写Makefile 从侧面说明了一个人是否具…...
享元模式flyweight
享元模式属于结构型模式。享元模式是池技术的重要实现方式,它可以减少重复对象的创建,使用缓存来共享对象,从而降低内存的使用。细粒度的对象其状态可以分为两种:内部状态和外部状态。应用场景系统存在大量相似或相同的对象。外部…...
Pulsar
一、简介Apache Pulsar是Apache软件基金会顶级项目,是下一代云原生分布式消息流平台,集消息、存储、轻量化函数式计算为一体,采用计算与存储分离架构设计,支持多租户、持久化存储、多机房跨区域数据复制,具有强一致性、…...

项目介绍 + 定长内存池设计及实现
你好,我是安然无虞。 文章目录项目介绍当前项目做的是什么?技术栈内存池是什么?池化技术内存池内存池主要解决的问题malloc定长内存池学习目的定长内存池设计项目介绍 当前项目做的是什么? 这个项目是实现一个高并发的内存池, 它的原型是 Google 的一个开源项…...

Linux--线程安全的单例模式--自旋锁--0211
1. 线程安全的单例模式 1.1 什么是单例模式 某些类, 只应该具有一个对象(实例), 就称之为单例. 1.1.1 懒汉方式实现单例模式 以上篇博文的线程池为例 Liunx--线程池的实现--0208 09_Gosolo!的博客-CSDN博客 实现懒汉模式首先要先将构造函数私有化,…...
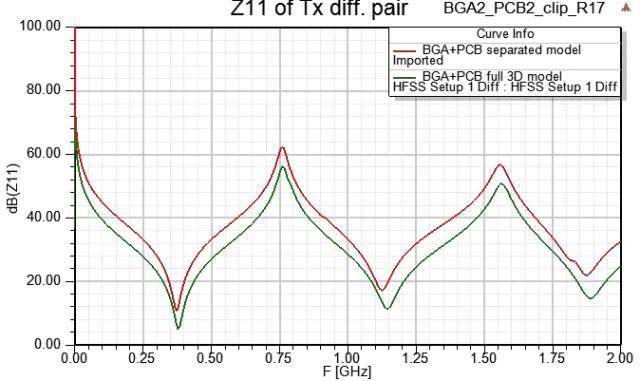
图文解说S参数(进阶篇)
S参数是RF工程师/SI工程师必须掌握的内容,业界已有多位大师写过关于S参数的文章,即便如此,在相关领域打滚多年的人, 可能还是会被一些问题困扰着。你懂S参数吗? 图文解说S参数(基础篇) 请继续往下看...台湾…...
Sentinel源码阅读
基础介绍 Sentinel 的使用可以分为两个部分: 核心库(Java 客户端):不依赖任何框架/库,能够运行于 Java 8 及以上的版本的运行时环境,同时对 Dubbo / Spring Cloud 等框架也有较好的支持(见 主流框架适配&…...
2023年浙江食品安全管理员考试真题题库及答案
百分百题库提供食品安全管理员考试试题、食品安全管理员考试预测题、食品安全管理员考试真题、食品安全管理员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、判断题 7.(重点)《餐饮服务食品安全…...
Webstorm 代码没有提示,uniapp 标签报错
问题 项目是用脚手架创建的: vue create -p dcloudio/uni-preset-vue my-project 打开之后,添加view标签警告报错的。代码也没有提示,按官方说法:CLI 工程默认带了 uni-app 语法提示和 5App 语法提示。 但是我这里就是有问题。…...

MySQL-Innodb引擎事务原理
文章目录1.事务介绍2 事务特性3. 事务的实现原理4 redo log 保证持久性5 undo log 保证原子性6 MVCC 概念6.1 隐藏字段6.2 版本链6.3 ReadView6.3.1readview 版本控制规则7 隔离性 实现7.2 隔离性- REPEATABLE READ 可重复读下8 一致性1.事务介绍 事务是一组操作的集合…...

Linux操作系统学习(了解环境变量)
文章目录环境变量初识除了上述介绍的PATH,还有一些常见的环境变量如:查看环境变量方法 :环境变量的基本概念:本地变量:环境变量初识 环境变量解释起来比较抽象,先看示例: #include <stdio.…...
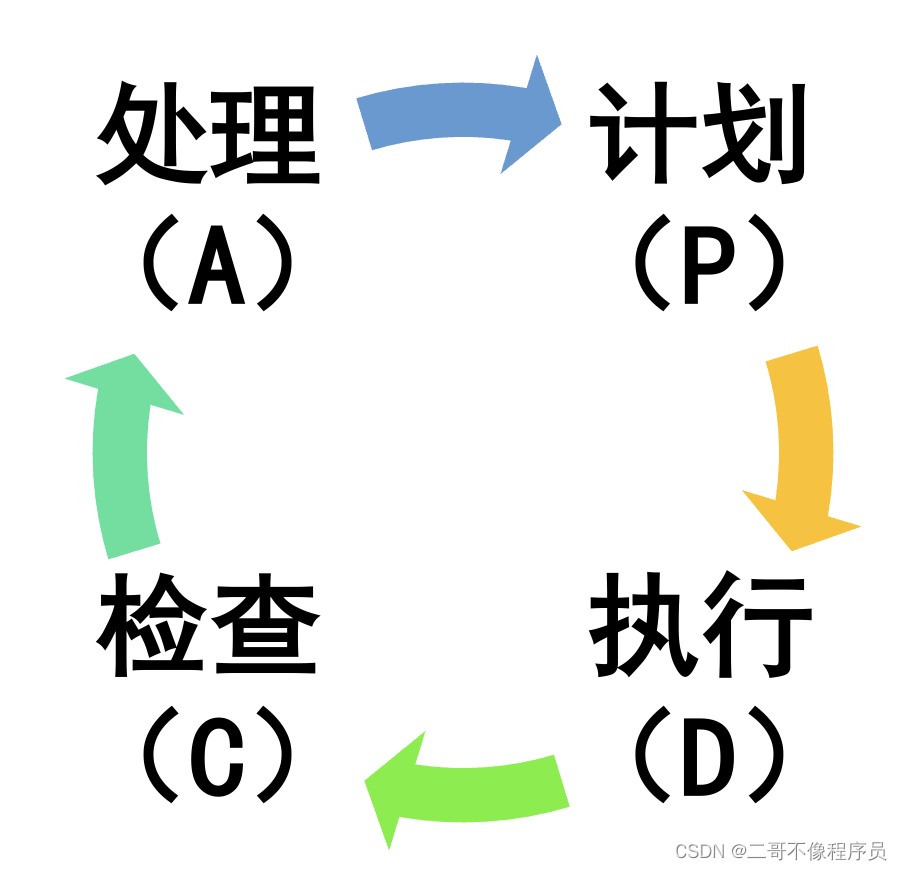
数据分析思维(六)|循环/闭环思维
循环/闭环思维 1、概念 在很多的分析场景下,我们需要按照一套流程反复分析,而不是进行一次性的分析,也就是说这套流程的结果会成为该流程的新一次输入,从而形成一个闭环,此时的分析思维我们称之为循环/闭环思维。 常…...

C++:类和对象(下)
文章目录1 再谈构造函数1.1 构造函数体赋值1.2 初始化列表1.3 explicit关键字2 static成员2.1 概念2.2 特性3 友元3.1 友元函数(流插入(<<)及流提取(>>)运算符重载)3.2 友元类4 内部类5 匿名对…...

ASP.NET Core MVC 项目 AOP之IResultFilter和IAsyncResultFilter
目录 一:说明 二:IActionFilter同步 三:IAsyncActionFilter异步 一:说明 IResultFilter同步过滤器与IAsyncResultFilter异步过滤器常常被用作于渲染视图或处理结果。 IResultFilter同步过滤器执行顺序: 1:执行控制器中的构造函数,实例化控制器 2:执行具体的Acti…...
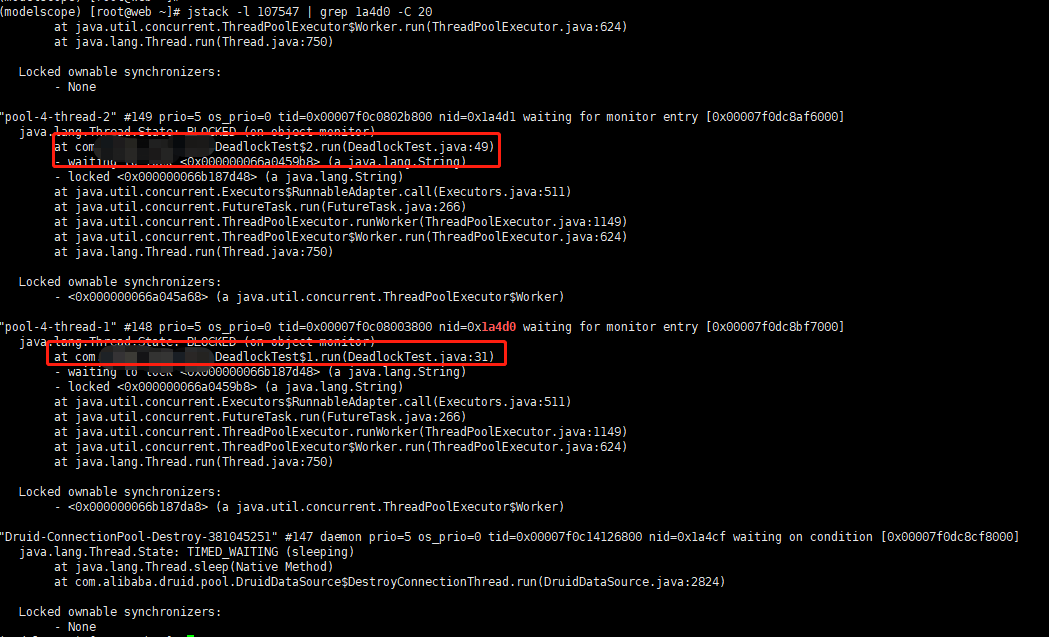
jstack排查cpu占用高[复习]
这样就可以看到占用CPU高的代码位置。 总结:就是先查到占用高的应用和具体的线程,然后根据线程到堆积信息查找即可。 不过堆栈信息非十进制,需提前把线程号转为十六进制。 这样就可以看到占用CPU高的代码位置。 总结:就是先查到…...
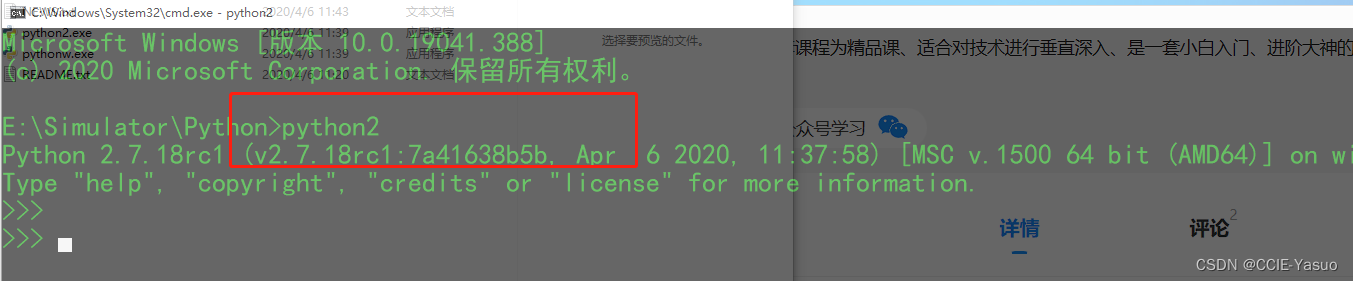
网络安全-Pyhton环境搭建
网络安全-Pyhton环境搭建 https://www.kali.org/get-kali/#kali-installer-images—kali官网下载地址 python这个东东呢 是目前来说最简单,方便的开源的脚本语言 广泛用于Web开发,AI,网站开发等领域 python要装2和3 为什么要安装两个版本…...

SpringBoot Mybatis 分页实战
pageInfo的属性 pageNum:当前页 pageSize:页面数据量 startRow:当前页首条数据为总数据的第几条 endRow:当前页最后一条数据为总数据的第几条 total:总数据量 pages:总页面数 listPage{}结果集 reasonable …...

计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性
计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性 Feasibility of Simultaneous Computed Tomographic Colonography and Fully Automated Bone Mineral Densitometry in a Single Examination 简单总结: 数据:患者的结肠镜检查和腹部CT检查…...
Java多级缓存是为了解决什么的?
前言 提到缓存,想必每一位软件工程师都不陌生,它是目前架构设计中提高性能最直接的方式。 缓存技术存在于应用场景的方方面面。从网站提高性能的角度分析,缓存可以放在浏览器,可以放在反向代理服务器,还可以放…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
