算法设计与分析(屈婉玲)视频笔记day2
序列求和的方法
数列求和公式
等差、等比数列与调和级数
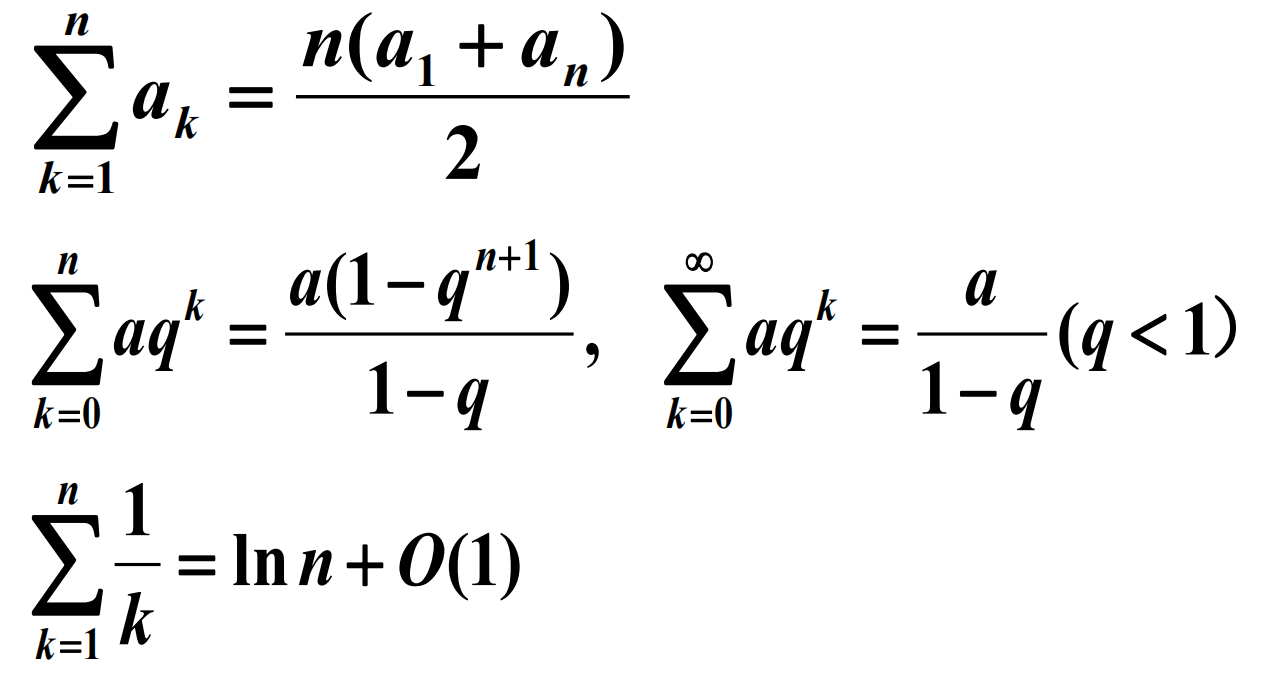
求和的例子

二分检索算法

二分检索运行实例
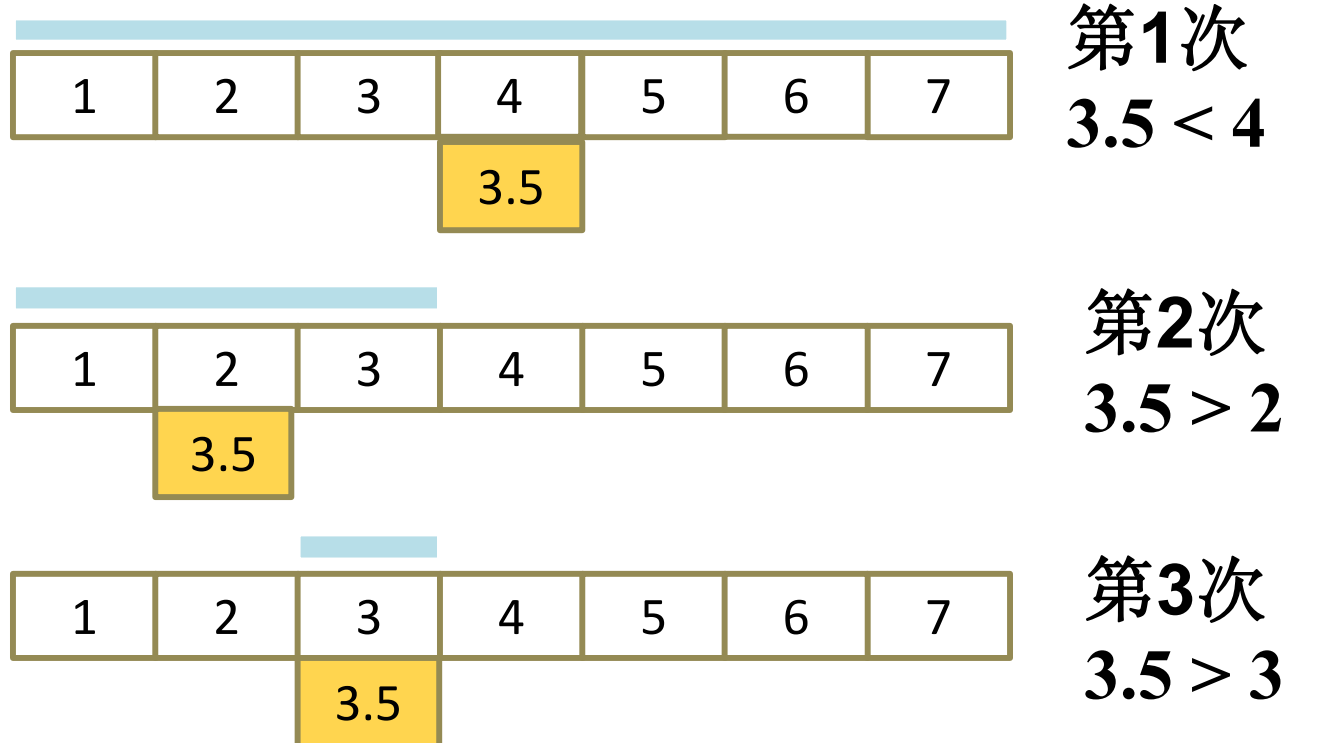
2 n +1个输入
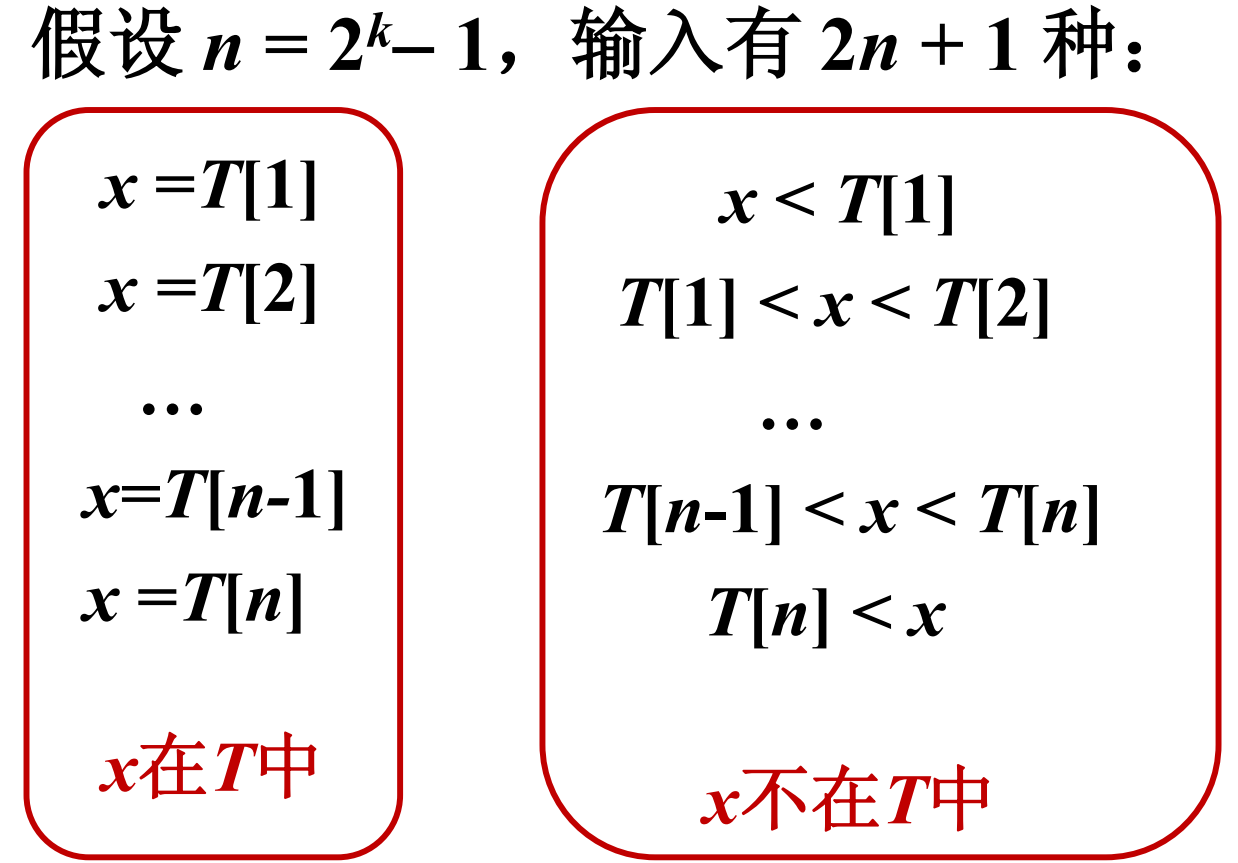
比较 t 次的输入个数
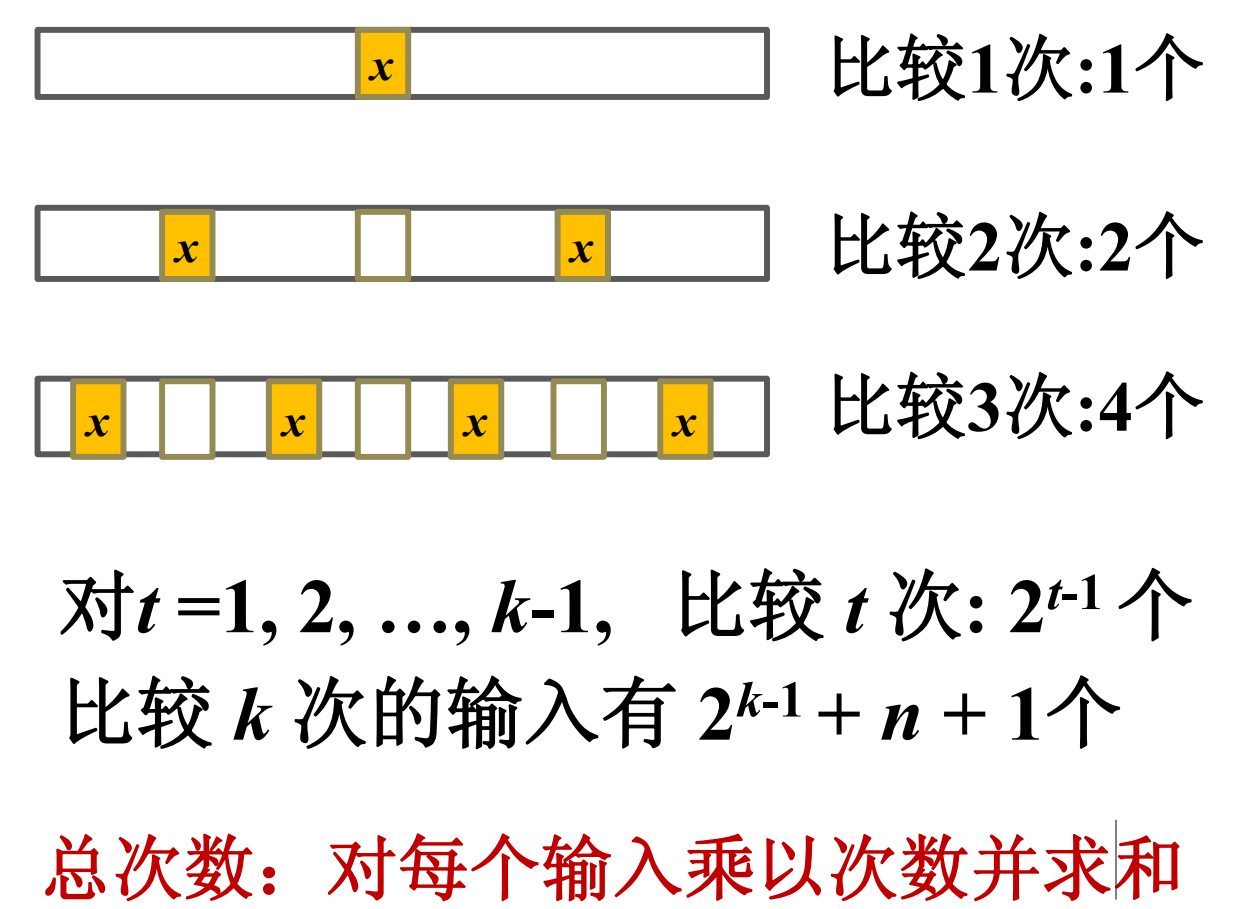
二分检索平均时间复杂度

估计和式上界的放大法
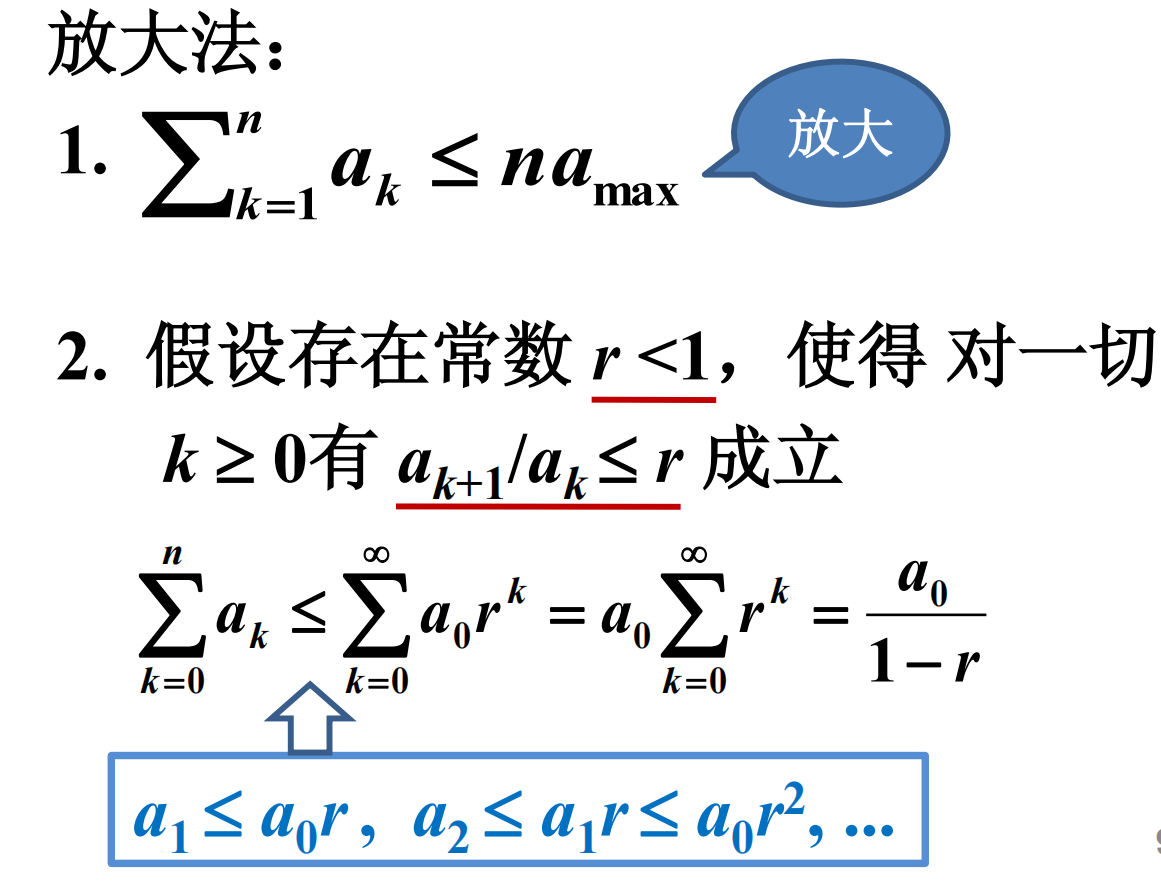
放大法的例子

估计和式渐近的界
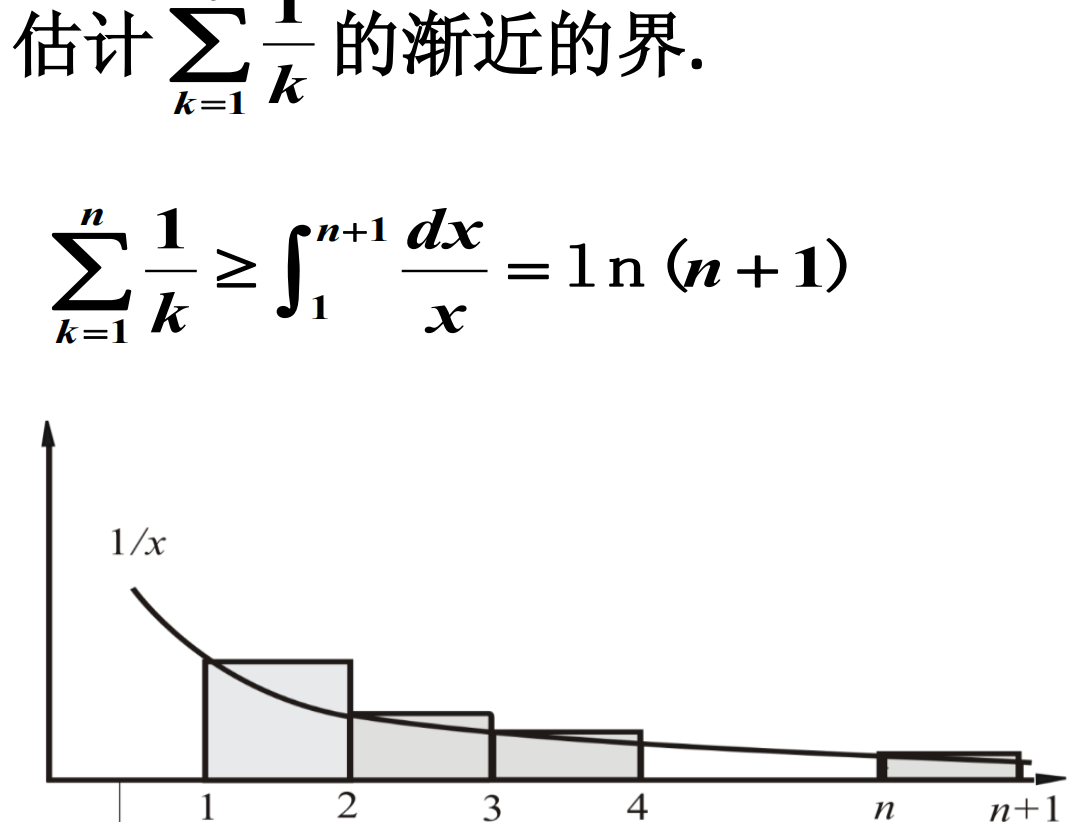
估计和式渐近的界
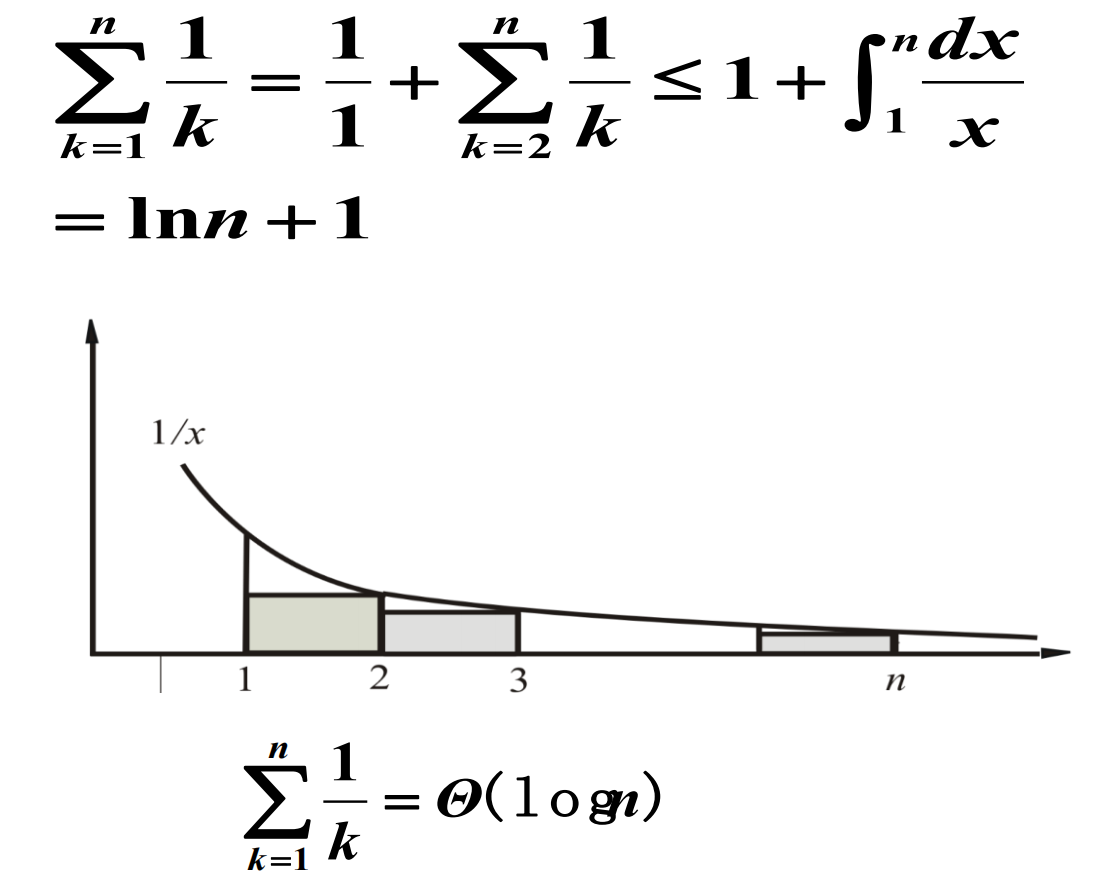
小结
• 序列求和基本公式:
等差数列
等比数列
调和级数
• 估计序列和:
放大法求上界
用积分做和式的渐近的界
• 应用:计数循环过程的基本运算次数
递推方程与算法分析
递推方程

递推方程的例子

Fibonacci数的存在
Hanoi塔问题
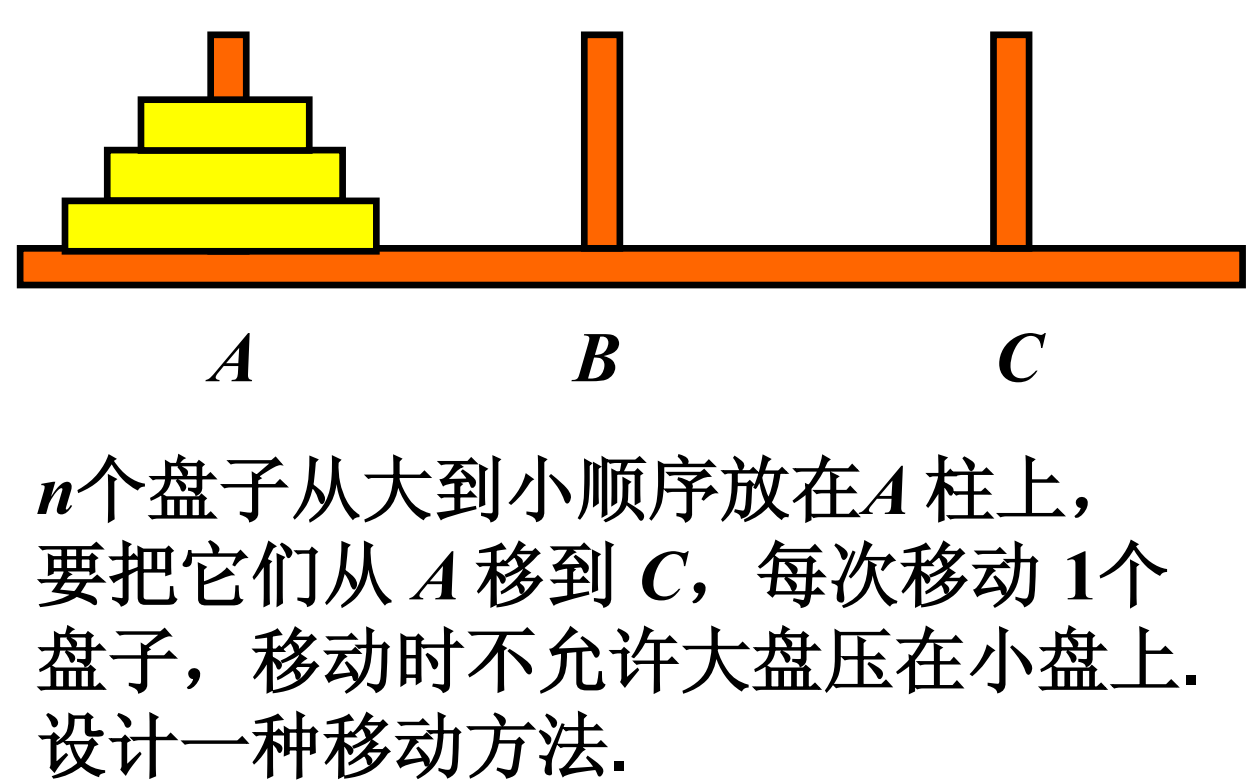
递归算法

分析算法

插入排序

最坏情况下时间复杂度
插入排序:
设基本运算是元素比较,对规模为 n
的输入最坏情况下的时间复杂度 W ( n )
W ( n )= W ( n -1)+ n -1 W (1)=0
解为 W ( n ) = n ( n -1)/2
小结
•递推方程的定义及初值
•递推方程与算法时间复杂度的关系
Hanoi塔的递归算法 插入排序的迭代算法
迭代法求解递推方程
迭代法
•不断用递推方程的右部替换左部
•每次替换,随着 n 的降低在和式中
多出一项
•直到出现初值停止迭代
•将初值代入并对和式求和
•可用数学归纳法验证解的正确性
Hanoi 塔算法

插入排序算法

换元迭代
•将对 n 的递推式换成对其他变元 k 的递推式
•对 k 直接迭代
•将解 (关于 k 的函数) 转换成关于 n 的函数
二分归并排序
MergeSort ( A , p , r )
输入:数组 A [ p … r ]
输出:按递增顺序排序的数组 A
1. if p < r
2. then q ( p+r )/2
3. MergeSort ( A , p , q )
4. MergeSort ( A , q +1, r )
换元
假设 n =2 k , 递推方程如下:
W ( n )=2 W ( n /2)+ n 1
W (1)=0
换元:
W (2 k ) = 2 W (2 k -1 ) + 2 k 1
W (0) = 0
迭代求解

解的正确性-归纳验证
证明 : 下述递推方程的解是 W ( n )= n ( n 1)/2
W ( n )= W ( n 1)+ n 1
W (1)=0
方法:数学归纳法
证 n =1 , W (1)=1 (1 1)/2 = 0
假设对于 *n , *解满足方程,则
W ( n +1)
= W ( n )+ n = n ( n 1)/2 + n
= n [( n 1)/2+1] = n ( n +1)/2
小结
迭代法求解递推方程
• 直接迭代,代入初值,然后求和
• 对递推方程和初值进行换元,然
后求和,求和后进行相反换元,
得到原始递推方程的解
• 验证方法——数学归纳法
差消法化简高阶递推方程
快速排序
• 假设 A [ p … r ] 的元素彼此不等
以首元素 A [1] 对数组 A [ p…r ] 划分 , 使得:
小于 x 的元素放在 A [ p … q 1]
大于 x 的元素放在 A [ q +1… r ]
• 递归对 A [ p … q 1] 和 A [ q +1… r ] 排序
工作量: 子问题工作量+划分工作量
输入情况
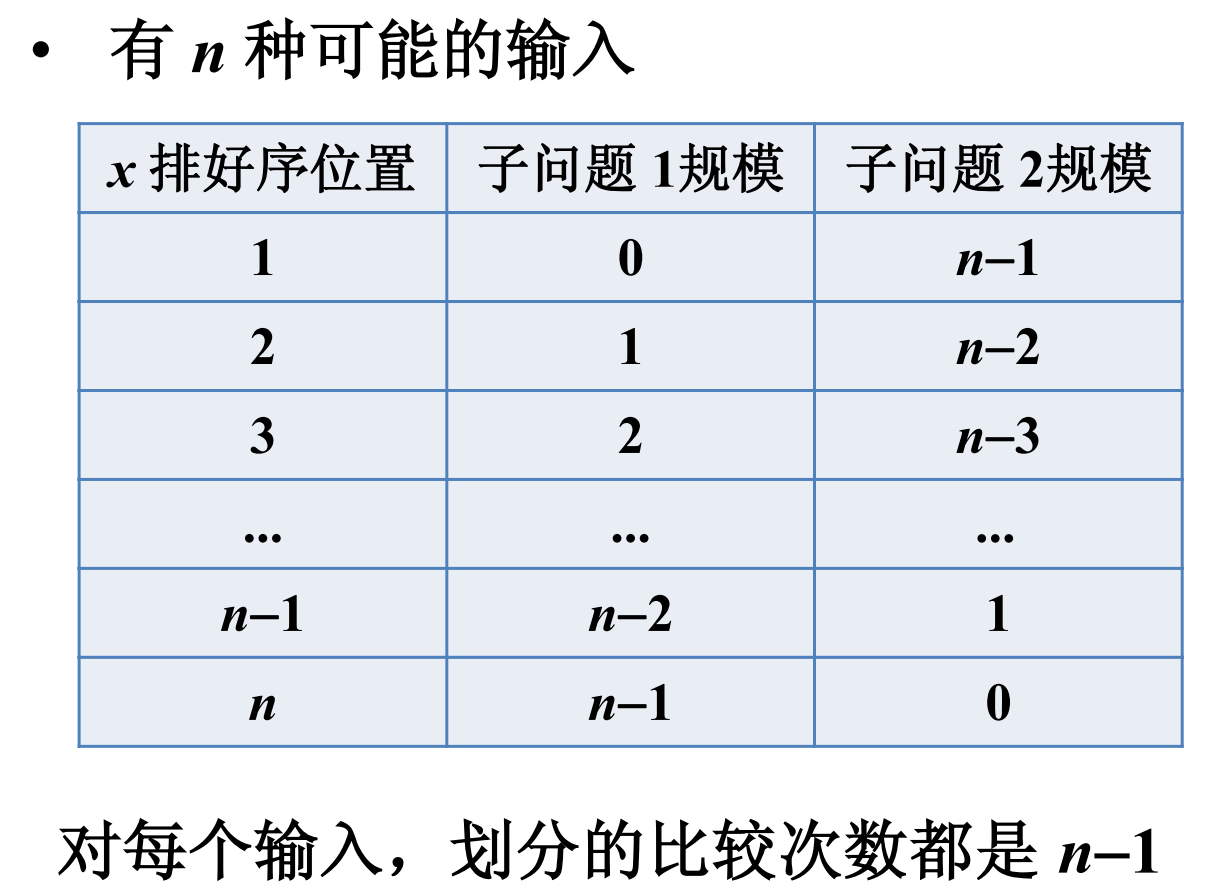
工作量总和
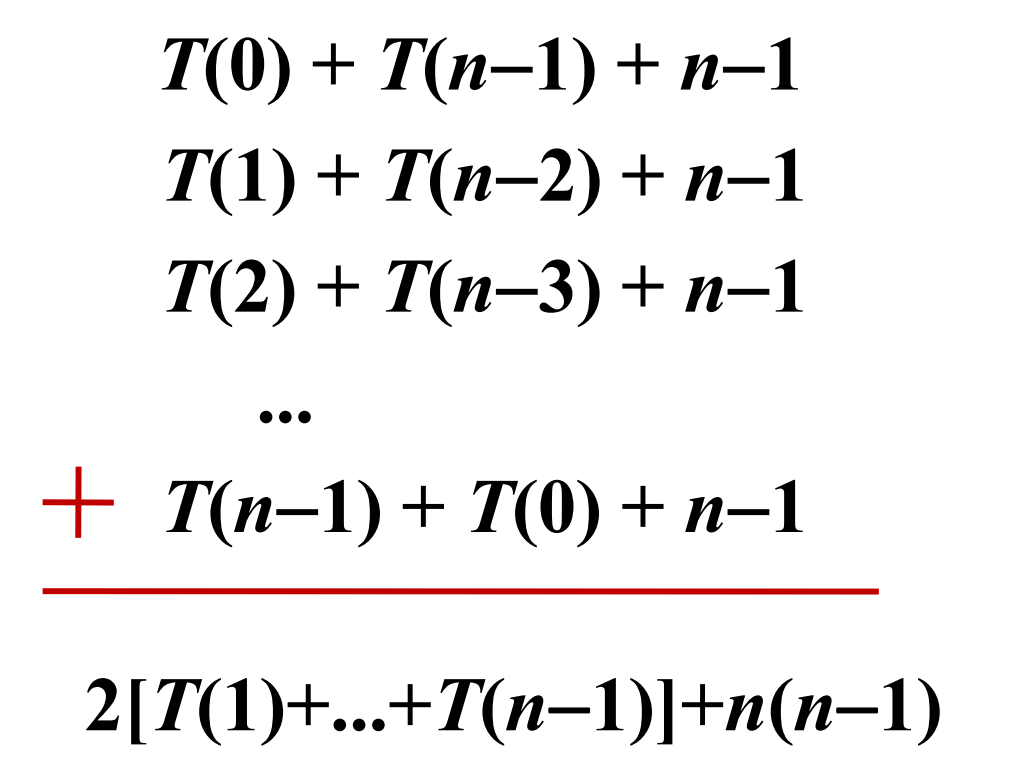
快速排序平均工作量
假设首元素排好序在每个位置是等
概率的
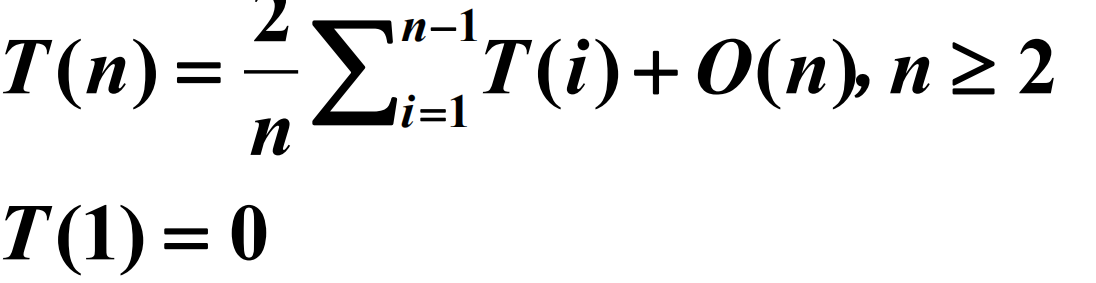
全部历史递推方程
对于高阶方程应该先化简,然后迭代
差消化简
利用两个方程相减,将右边的项尽可能
消去,以达到降阶的目的
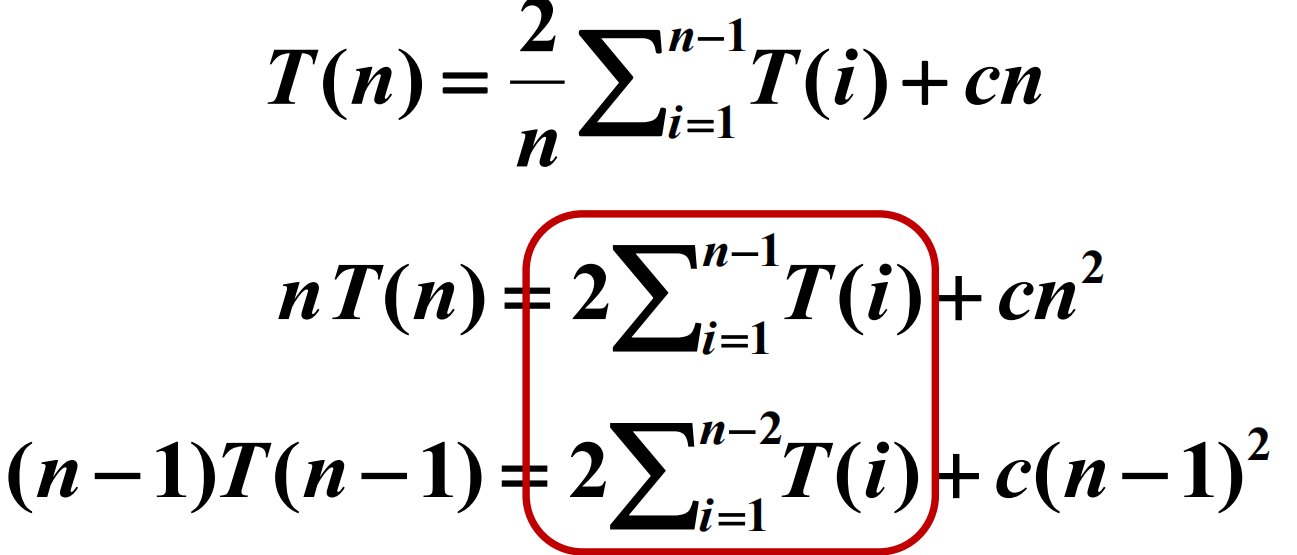
差消化简

迭代求解

小结
• 对于高阶递推方程先要用差消法化简为一阶方程
• 迭代求解
递归树
有关基 递归树的概念 本概
• 递归树是迭代计算的模型 .
• 递归树的生成过程与迭代过程一致 .
• 递归树上所有项恰好是迭代之后产
生和式中的项 .
• 对递归树上的项求和就是迭代后方
程的解.
迭代在递归树中的表示
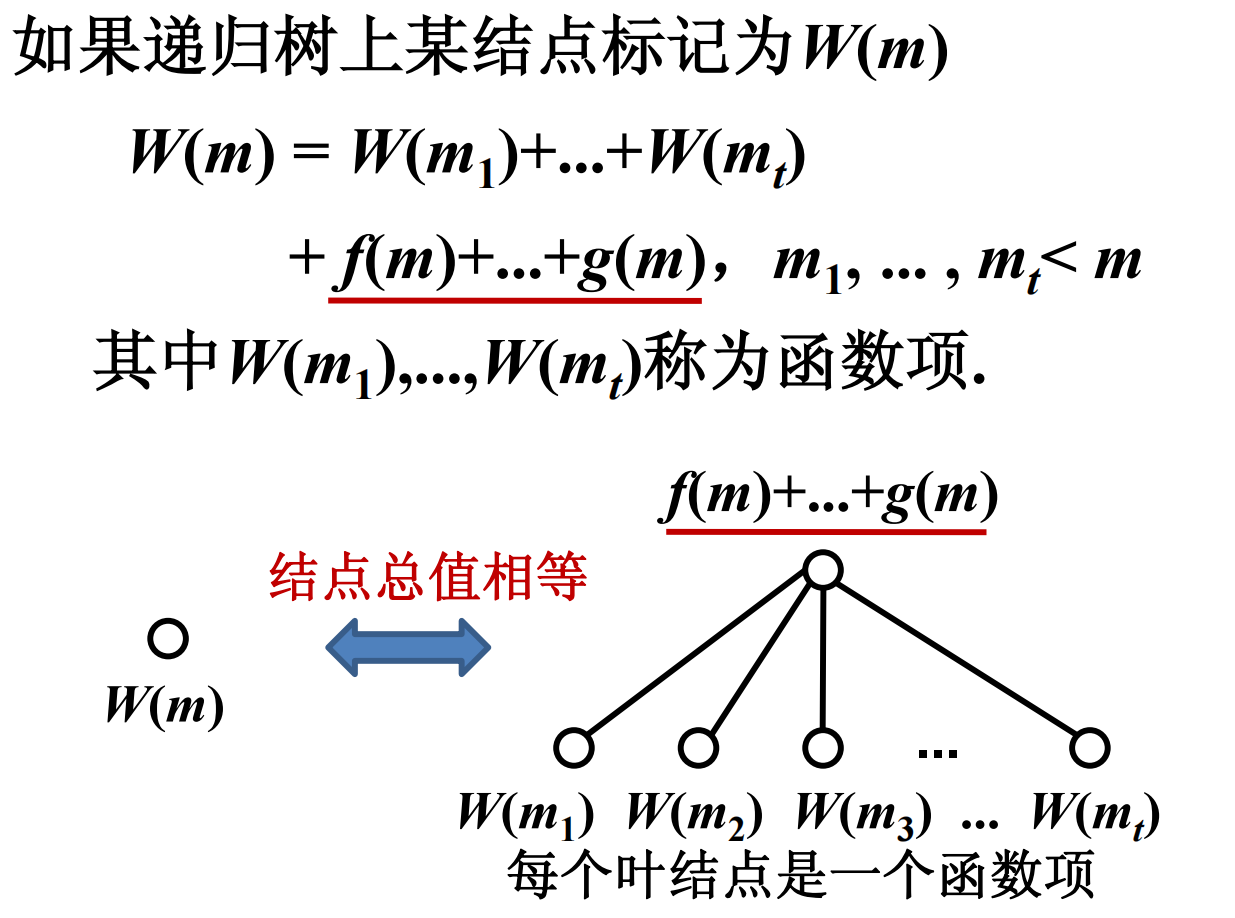
二层子树的例子
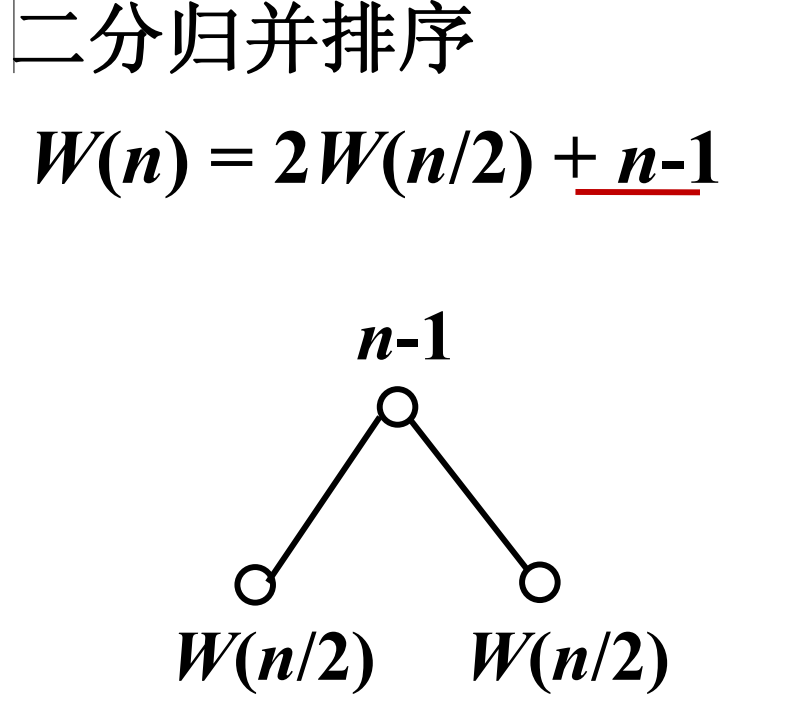
递归树的生成规则
• 初始,递归树只有根结点 , 其值为 W ( n )
• 不断继续下述过程:
将函数项叶结点的迭代式 W ( m ) 表示成二
层子树
用该子树替换该叶结点
• 继续递归树的生成,直到树中无函数项
(只有初值)为止.
递归树生成实例
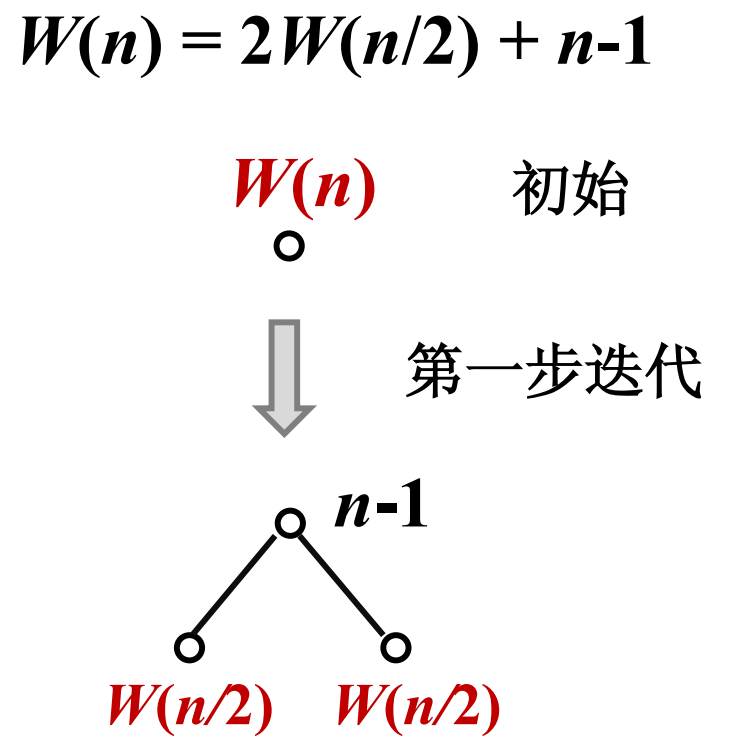
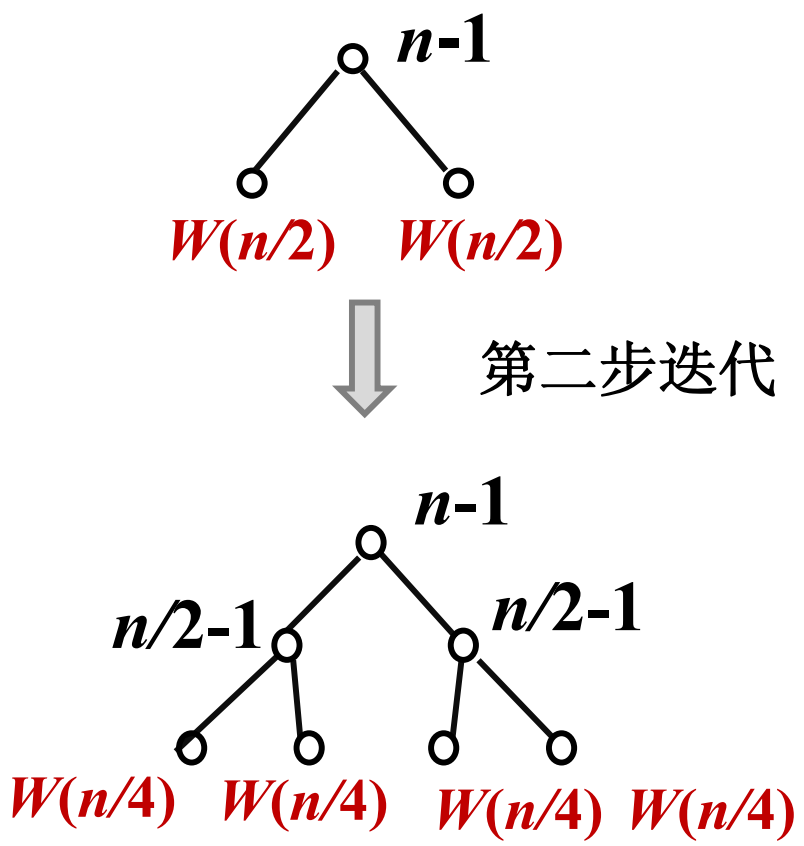
递归树
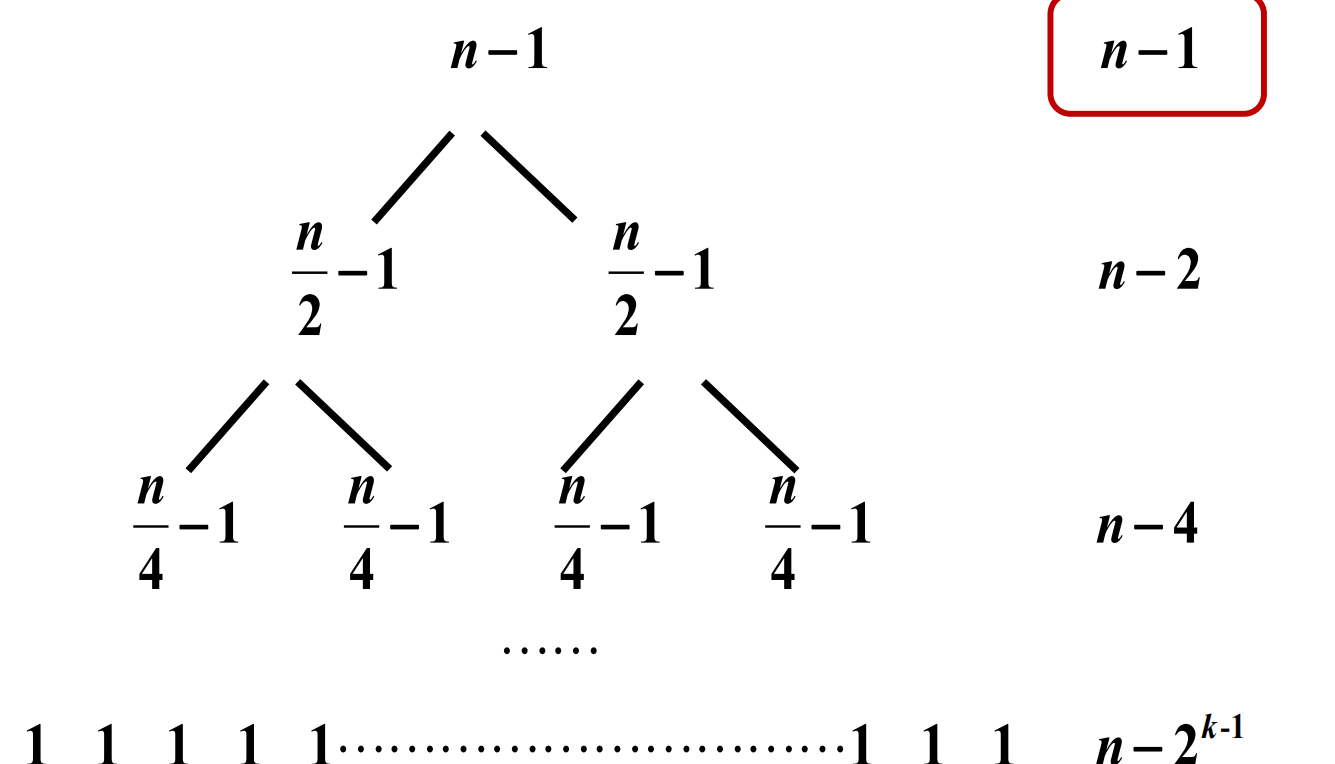
对递归树上的量求和
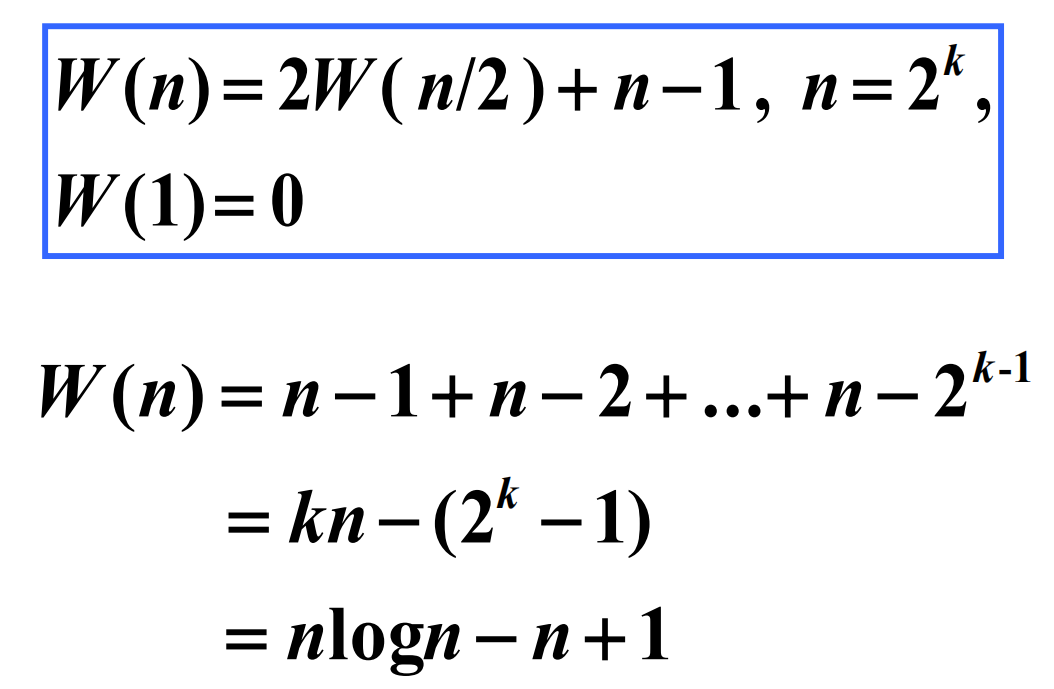
递归树应用实例
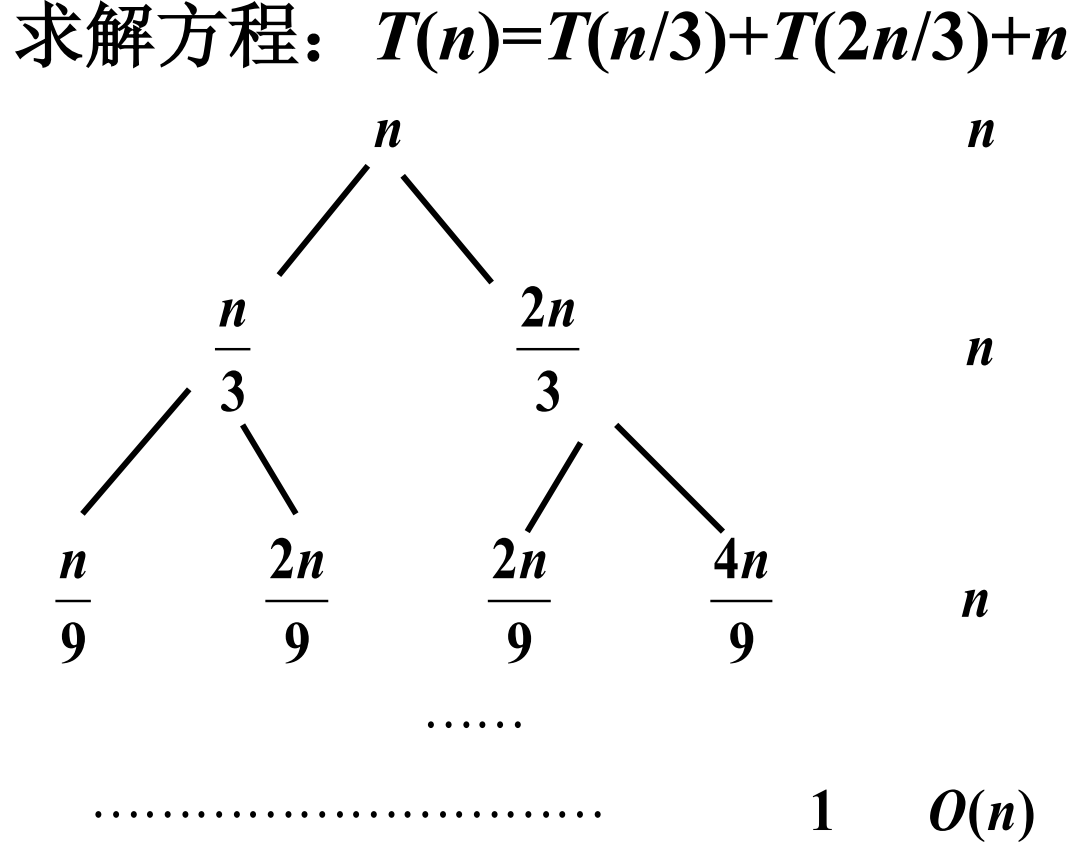
求和
方程: T ( n )= T ( n /3)+ T (2 n /3)+ n
递归树层数 k ,每层 O ( n )
******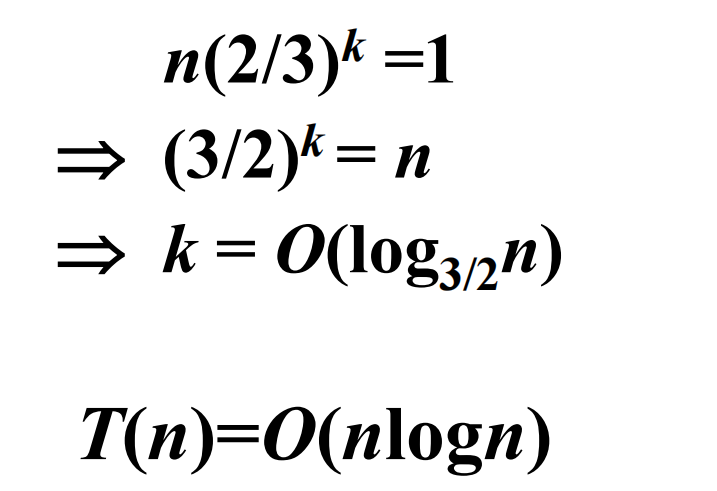
小结
• 递归树是迭代的图形表述
• 递归树的生成规则
• 如何利用递归树求解递推方程?
主定理及其证明
主定理的应用背景
求解递推方程
T ( n ) = a T ( n / b ) + f ( n )
a : 归约后的子问题个数
n/b :归约后子问题的规模
f ( n ) :归约过程及组合子问题的解的
工作量
二分检索: T ( n ) = T ( n /2)+1
二分归并排序: T ( n ) =2 T ( n /2)+ n -1
主定理

迭代

迭代结果



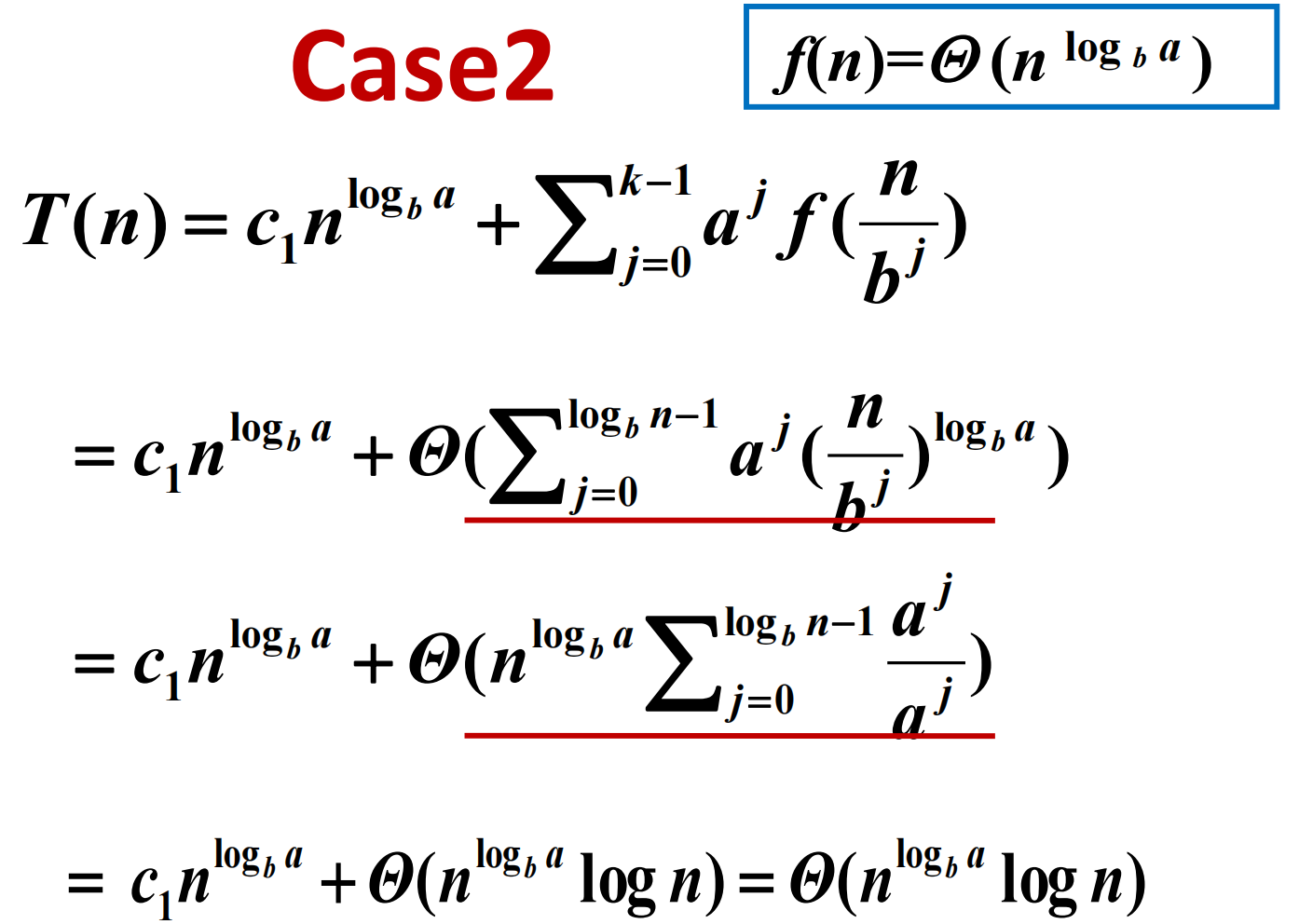


小结
• 主定理的应用背景
• 主定理的内容
• 主定理的证明
主定理的应用
求解递推方程:例1
例 1 求解递推方程
T ( n ) = 9 T ( n /3) + n
解 上述递推方程中的
a = 9 , b = 3 , f ( n ) = n
n log 3 9 = n 2 , f ( n ) = O ( n log 3 9-1 )
相当于主定理的 case1 ,其中 =1.
根据定理得到 T ( n ) = ( n 2 )
求解递推放出:例2
例 2 求解递推方程
T ( n ) = T (2 n /3) + 1
****求解递推方程:例2
解 上述递推方程中的
a = 1, b = 3/2, f ( n ) = 1 ,
n log 3/2 1 = n 0 = 1
相当于主定理的
Case2 .
根据定理得到 T ( n ) = ( log n )

条件验证

递归算法分析

不能使用主定理的例子

递归树求解
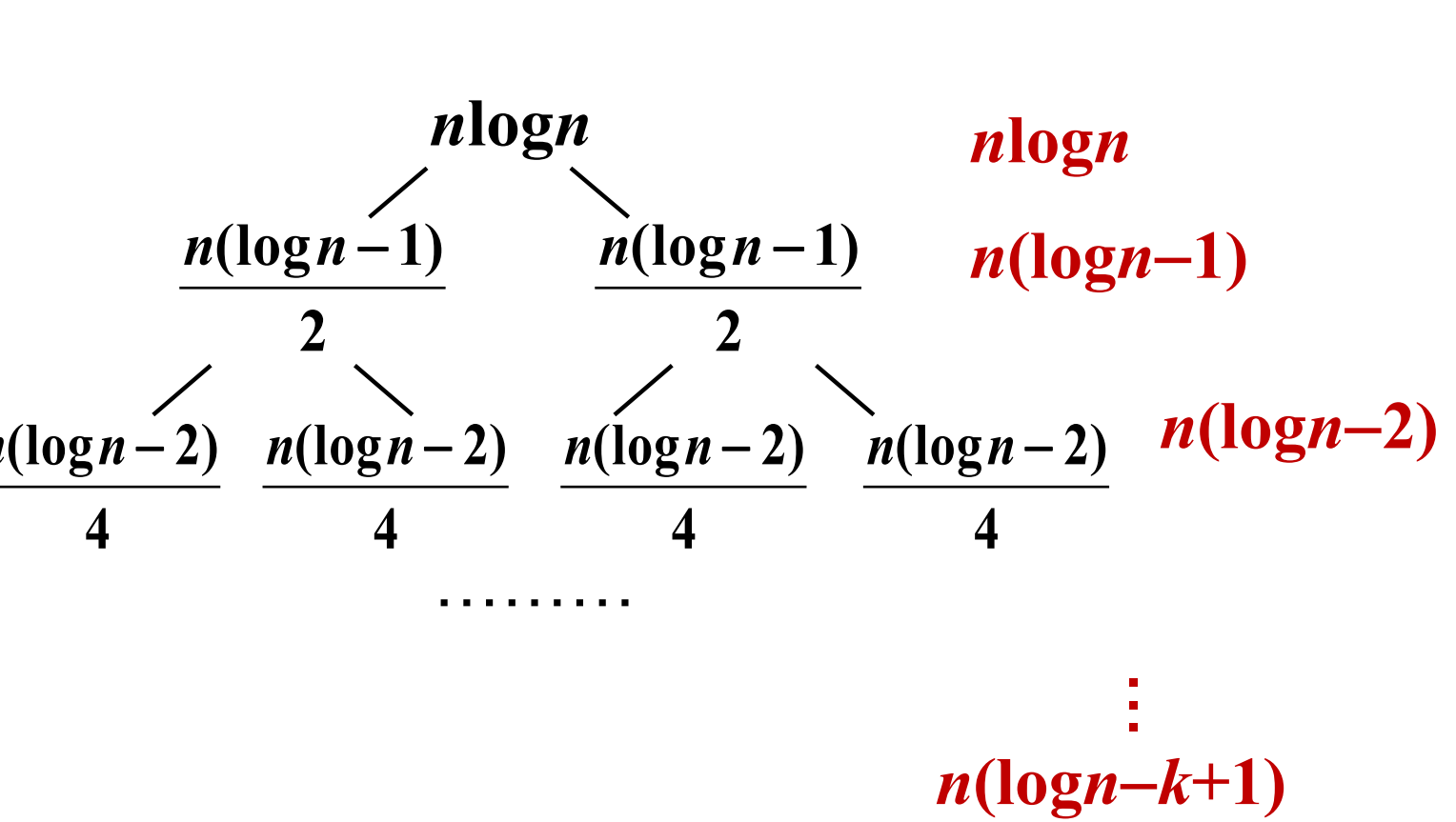
求和
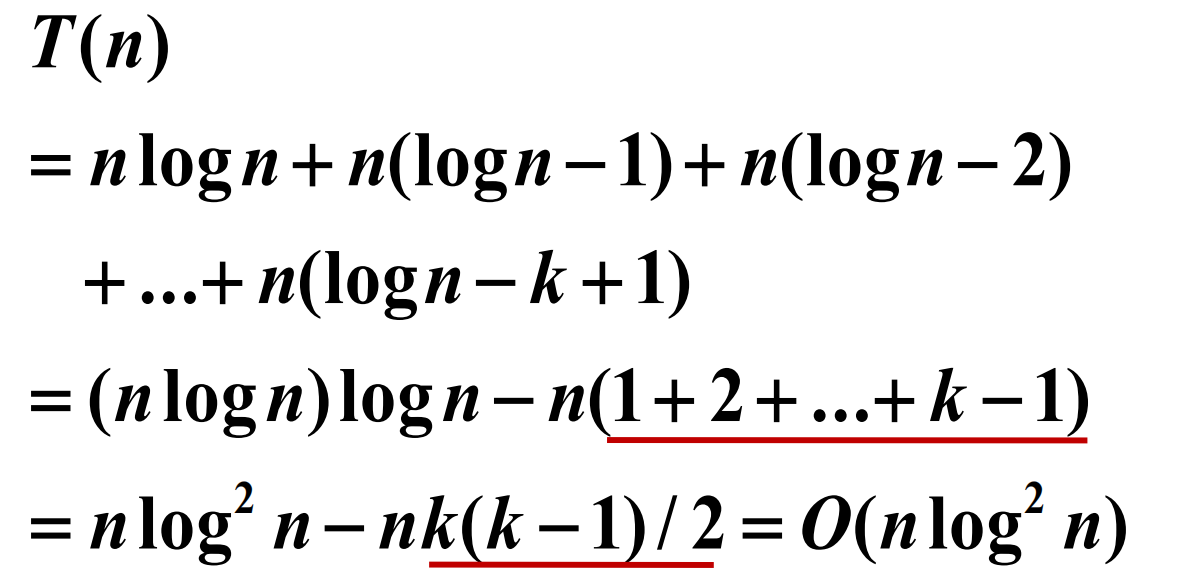
小结
• 使用主定理求解递推方程需要
满足什么条件?
• 主定理怎样用于算法复杂度分
析?
相关文章:
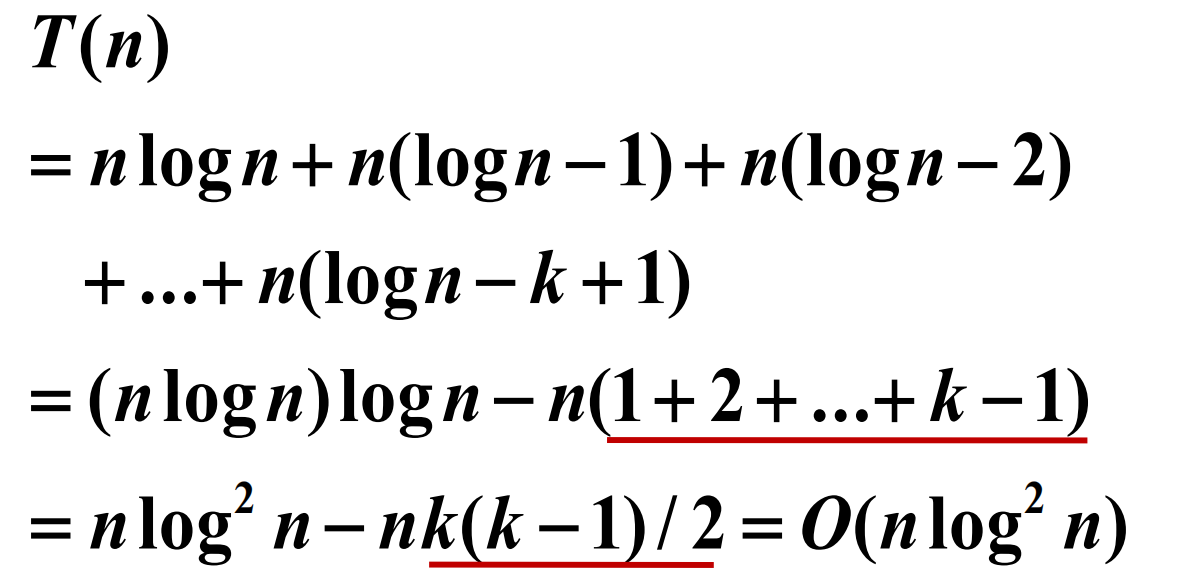
算法设计与分析(屈婉玲)视频笔记day2
序列求和的方法 数列求和公式 等差、等比数列与调和级数 求和的例子 二分检索算法 二分检索运行实例 2 n 1个输入 比较 t 次的输入个数 二分检索平均时间复杂度 估计和式上界的放大法 放大法的例子 估计和式渐近的界 估计和式渐近的界 小结 • 序列求和基本公式:…...

14-PHP使用过的函数 131-140
131、session_unset 释放当前会话注册的所有会话变量。 没有返回值。 132、session_destroy 销毁当前会话中的全部数据, 但是不会重置当前会话所关联的全局变量, 也不会重置会话 cookie。 如果需要再次使用会话变量, 必须重新调用 session_…...

【第39天】实现一个冒泡排序
本文已收录于专栏 🌸《Java入门一百例》🌸 学习指引 序、专栏前言一、冒泡排序一、【例题1】1、题目描述2、解题思路3、模板代码三、推荐专栏序、专栏前言 本专栏开启,目的在于帮助大家更好的掌握学习Java,特别是一些Java学习者难以在网上找到系统地算法学习资料帮助自身…...

「2」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 方阵的行列式 (1) |A^T||A|(2) |ǖ…...

动态规划专题——背包问题
🧑💻 文章作者:Iareges 🔗 博客主页:https://blog.csdn.net/raelum ⚠️ 转载请注明出处 目录前言一、01背包1.1 使用滚动数组优化二、完全背包2.1 使用滚动数组优化三、多重背包3.1 使用二进制优化四、分组背包总结…...

数据的分组聚合
1:分组 t.groupby #coding:utf-8 import pandas as pd import numpy as np file_path./starbucks_store_worldwide.csv dfpd.read_csv(file_path) #print(df.head(1)) #print(df.info()) groupeddf.groupby(byCountry) print(grouped) #DataFrameGroupBy #可以遍历…...
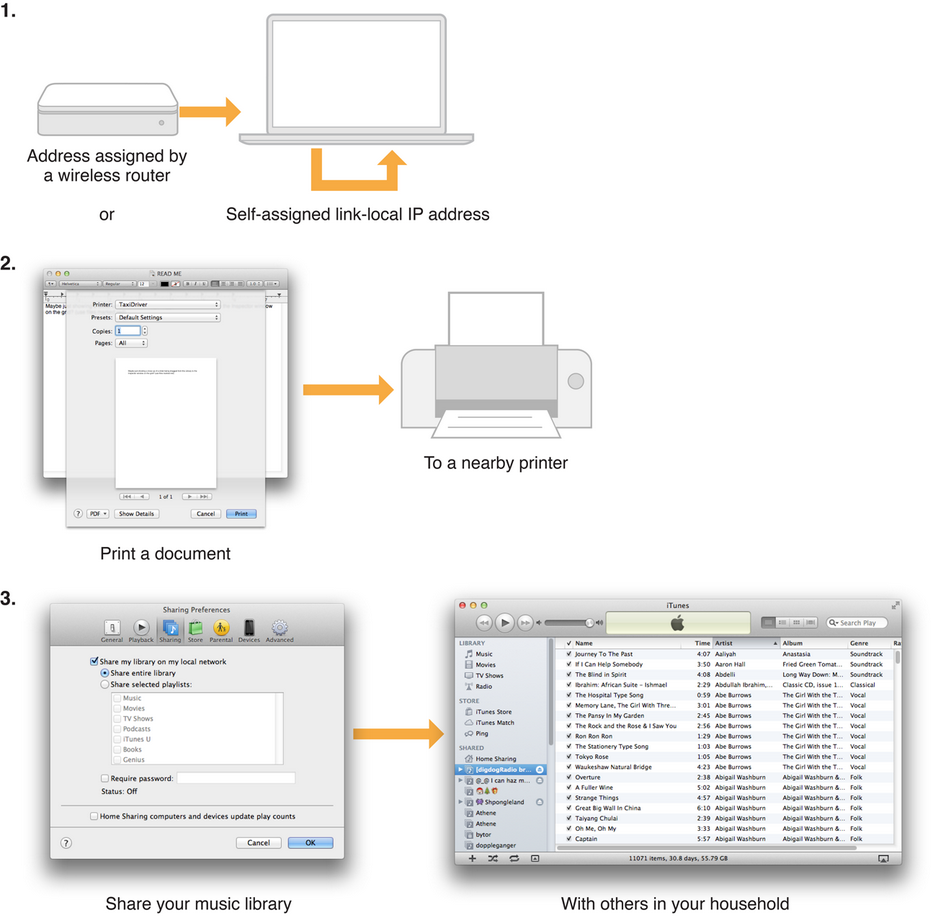
【Airplay_BCT】Bonjour conformance tests苹果IOT
从Airplay开始,接触到BCT,这是什么?被迫从安卓变成ios用户和开发。。。开始我的学习之旅,记录成长过程,不定时更新 Bonjour 下面是苹果官网关于bonjour的解释 Bonjour, also known as zero-configuration networking, …...
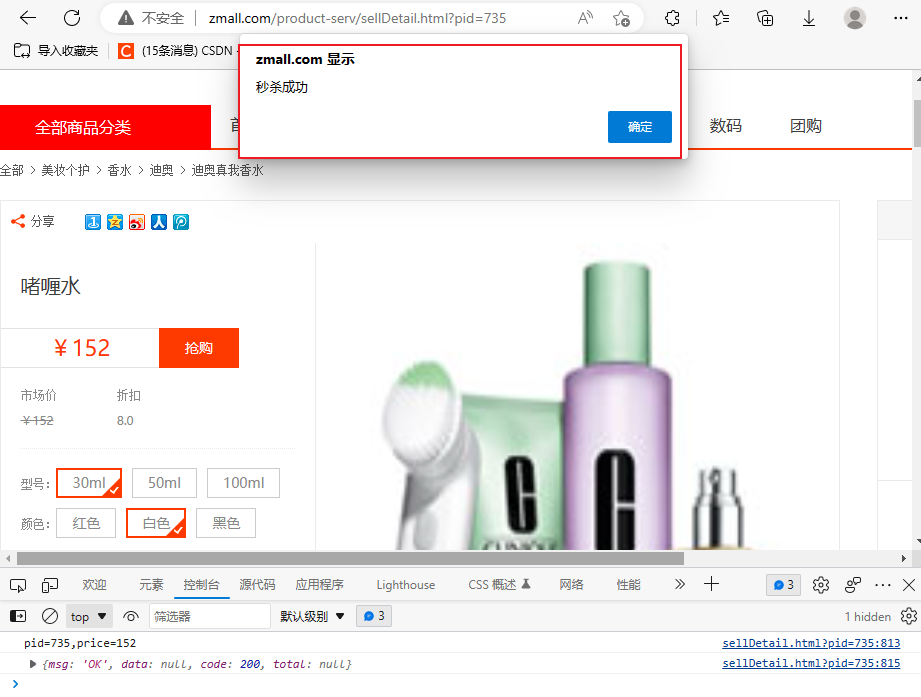
开发微服务电商项目演示(五)
登录方式调整第1步:从zmall-common的pom.xml中移除spring-session-data-redis依赖注意:本章节中不采用spring-session方式,改用redis直接存储用户登录信息,主要是为了方便之后的jmeter压测;2)这里只注释调用…...

Git删除大文件历史记录
Git删除大文件历史记录 git clone 仓库地址 查看大文件并排序 git rev-list --objects --all |grep $(git verify-pack -v .git/objects/pack/pack-*.idx | sort -k 3 -g | tail -1|awk {print $1})删除大文件 git filter-branch --force --index-filter git rm --cached --ig…...
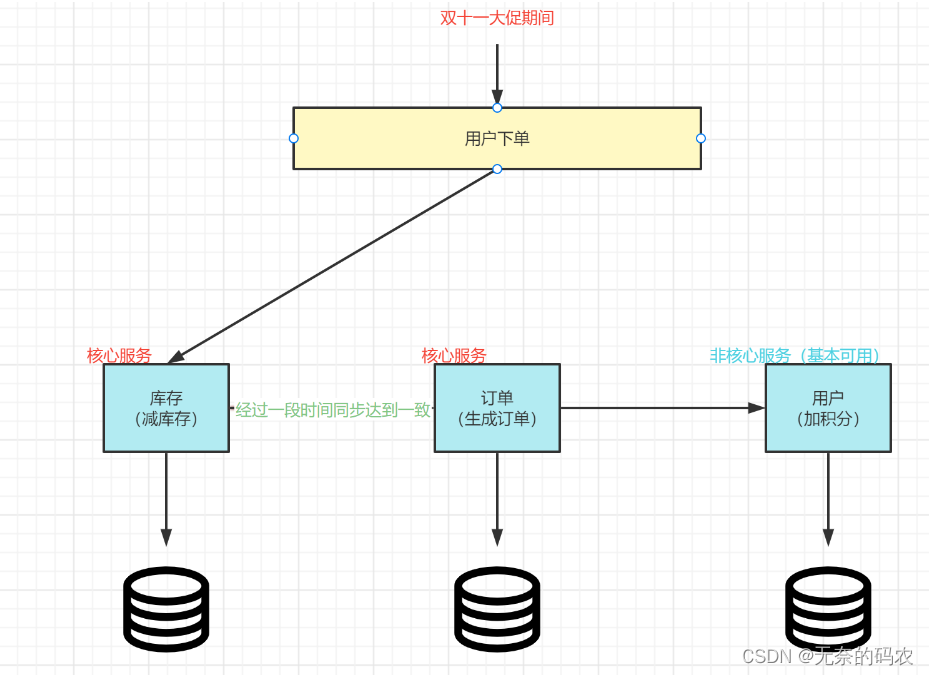
Seata-Server分布式事务原理加源码(一) - 微服务之分布式事务原理
概念 基础概念:事务ACID • A(Atomic):原子性,构成事务的所有操作,要么都执行完成,要么全部不执行,不可能出现部分成功部分失 败的情况。 • C(Consistency)…...

【ZooKeeper】zookeeper源码9-ZooKeeper读写流程源码分析
源码项目zookeeper-3.6.3:核心工作流程ZooKeeper选举和状态同步结束之后的服务启动ZooKeeper SessionTracker启动和工作机制ZooKeeper选举和状态同步结束之后的服务启动 在Leader的lead()方法的最后,即Leader完成了和集群过半Follower的同步之后&#x…...

Python实现批量导入xlsx数据1000条
遇到的问题:用户批量导入数据1000条,导入不成功的问题,提示查询不到商品资料。这个场景需要依靠批量的数据,每次测试的时候需要手动生成批量的数据,然后再导入操作,费时费劲。所以写了个脚本来实现。在前面…...
Ubuntu20.04安装redis与远程连接
一、安装Redis5.7 1、安装Redis apt-get install redis-server2、安装完成后,Redis服务器会自动启动。查看redis是否启动成功 service redis-server status #查看状态如下显示Active:active(running)状态:表示redis已在运行,启动成功。 …...

SAS应用入门学习笔记5
input 操作符: 代码说明: 1)1 表示第1列字符;7表示第7列字符; 2)col1 表示第一列数据;col2 表示第二列数据; 3)4.2 表示的是4个字符,2表示小数点后两位&a…...
PHP新特性集合
php8新特性命名参数function foo(string $a, string $b, ?string $c null, ?string $d null) { /* … */ }你可以通过下面的方式传入参数进行调用foo(b: value b, a: value a, d: value d, );联合类型php7class Number {/** var int|float */private $number;/*** param f…...
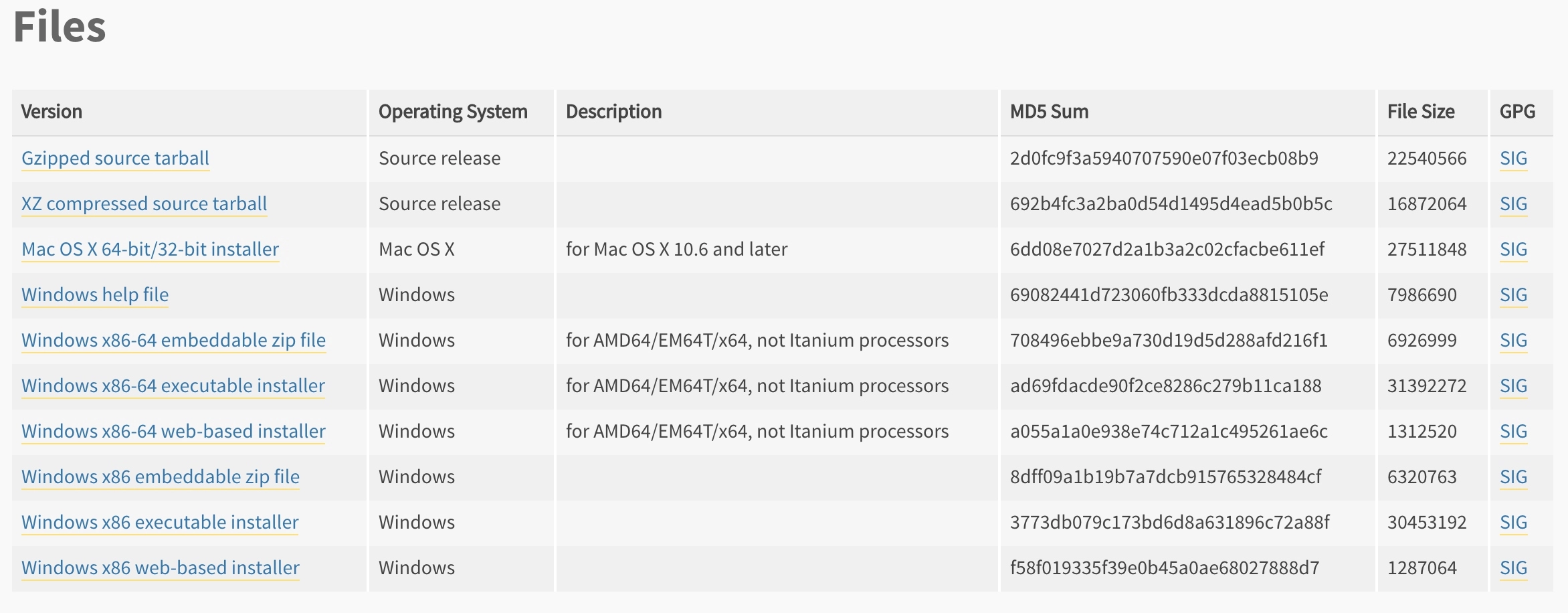
【开发环境配置】--Python3的安装
1-开发环境配置 工欲善其事,必先利其器! 编写和运行程序之前,我们必须先把开发环境配置好。只有配置好了环境并且有了更方便的开发工具,我们才能更加高效地用程序实现相应的功能。然而很多情况下,我们可能在最开始就…...

postman实现接口测试详细教程
各位小伙伴大家好, 今天为大家带来postman实战接口测试详细教程 一、通过接口文档集合抓包分析接口 通过fiddler抓包获取到注册接口URL地址及相关参数数据,并通过接口文档分析接口参数内容及参数说明, 如有必要的依赖条件必须进行梳理, 如token等 Fiddler抓包注册接口请求与…...
使用crontab执行定时任务
本来这个东西是挺简单的,是我脑子一直没转过来弯,我就想看看有多少人跟我一样😏 crontab语法自己去菜鸟教程看看就知道了,没什么难度 需求:每分钟定时执行一个PHP文件或者一个PHP命令 这是需要执行的文件࿰…...
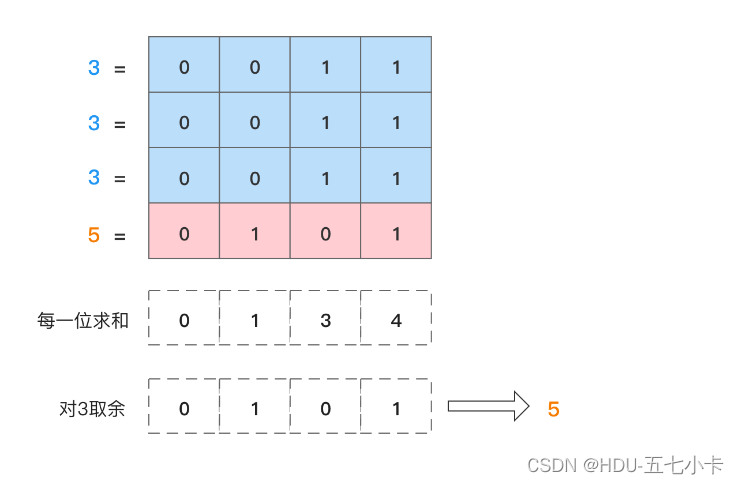
剑指 Offer 56 - II. 数组中数字出现的次数 II
题目 在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。 思路 这题是剑指 Offer 56 - I. 数组中数字出现的次数的变体,本题只有一个数num出现一次,其余的均出现三次 三次的话使用异或消无法…...

C语言学习笔记(八): 自定义数据类型
结构体变量 什么是结构体 C语言允许用户自己建立由不同类型数据组成的组合型的数据结构,它称为结构体 结构体的成员可以是任何类型的变量,如整数,字符串,浮点数,其他结构体,指针等 struct Student //s…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...

今日行情明日机会——20250609
上证指数放量上涨,接近3400点,个股涨多跌少。 深证放量上涨,但有个小上影线,相对上证走势更弱。 2025年6月9日涨停股主要行业方向分析(基于最新图片数据) 1. 医药(11家涨停) 代表标…...
