【代码随想录训练营】【Day14】第六章|二叉树|理论基础|递归遍历|迭代遍历|统一迭代
理论基础
二叉树的定义形式有:节点指针和数组
- 在数组中,父节点的下标为
i,那么其左孩子的下标即i*2+1,右孩子的下标即为i*2+2
二叉树的常见遍历形式有:前序遍历、后序遍历、中序遍历和层序遍历
- 前序遍历:二叉树的节点遍历顺序为,根节点、左节点、右节点,常记为“根左右”
- 同理后序遍历则为“左右根”,中序遍历则为“左根右”,其主要的区别在于“根节点”的遍历顺序
- 但是注意,访问顺序和遍历顺序不是相同的概念,例如中序遍历应该理解为已访问过中节点,只是未处理它,需要优先处理它的左节点
- 层序遍历:顾名思义,就是按照从根节点到叶节点、从左到右的顺序,一层一层地遍历节点
根据二叉树的定义不同,又可分为不同类型的二叉树,常见的有:
- 满二叉树:只有度为0的结点和度为2的节点,并且度为0的结点都在同一层上。
- 完全二叉树:整颗树(包括其每一棵子树)
除了叶节点,其他每一个节点都有左右节点(节点不为空),同时要保证父子节点的顺序关系。 - 二叉搜索树:整颗树(包括其每一棵子树)都满足
左节点 < 父节点,右节点 > 父节点的条件,其中序遍历的结果为递增序列。 - 二叉平衡树:整颗树(包括其每一棵子树)每一个节点都满足
|其左右节点的树的高度的差值| <= 1
更多有关二叉树的理论基础可查阅:《代码随想录》二叉树理论基础
对于二叉树的遍历在《代码随想录》中都有非常详细的解释,我也是阅读学习之后再来解题的,所以在下面的解题过程中就不加以赘述了,仅贴出实现不同遍历形式的程序代码。
递归遍历二叉树
Java解法(递归,前序遍历):
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.preorder(root, ans);return ans;}public void preorder(TreeNode root, List<Integer> list){if(null == root){return;}list.add(root.val);this.preorder(root.left, list);this.preorder(root.right, list);}
}
Java解法(递归,中序遍历):
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.inorder(root, ans);return ans;}public void inorder(TreeNode root, List<Integer> list){if(null == root){return;}this.inorder(root.left, list);list.add(root.val);this.inorder(root.right, list);}
}
Java解法(递归,后序遍历):
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.postorder(root, ans);return ans;}public void postorder(TreeNode root, List<Integer> list){if(null == root){return;}this.postorder(root.left, list);this.postorder(root.right, list);list.add(root.val);}
}
迭代遍历二叉树
Java解法(迭代,前序遍历):
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.preorder(root, ans);return ans;}public void preorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.pop();list.add(root.val);if(null != root.right) stack.push(root.right);if(null != root.left) stack.push(root.left);}}
}
Java解法(迭代,中序遍历):
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.inorder(root, ans);return ans;}public void inorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();while(null != root || !stack.isEmpty()){if(null != root){stack.push(root);root = root.left;}else{root = stack.pop();list.add(root.val);root = root.right;}}}
}
Java解法(迭代,后序遍历):
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.postorder(root, ans);return ans;}public void postorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.pop();list.add(root.val);if(null != root.left) stack.push(root.left);if(null != root.right) stack.push(root.right);}Collections.reverse(list);}
}
我们发现迭代法实现的先中后序,其实风格也不是那么统一,除了先序和后序,有关联,中序完全就是另一个风格了,一会用栈遍历,一会又用指针来遍历。那么如何针对三种不同的遍历方式,使用迭代法是可以写出统一风格的代码?
统一迭代遍历二叉树【重点】
可以利用标记法来做到统一迭代:
- 将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
- 在这里,我们利用空指针来做标记,在要处理的节点放入栈之后,紧接着放入一个空指针作为标记。
- 详细的解释和实现可以查阅:《代码随想录》二叉树的统一迭代法
Java解法(统一迭代,前序遍历):
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.preorder(root, ans);return ans;}public void preorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.peek();if(null != root){stack.pop(); // 需要先弹出节点,避免后续重复访问// 节点按照右左根的顺序进栈,后续出栈顺序为根左右(前序遍历)if(null != root.right) stack.push(root.right);if(null != root.left) stack.push(root.left);stack.push(root);stack.push(null); // 对需要处理的节点,在其后面跟上空指针作为标记}else{stack.pop(); // 遇到标记时,先弹出标记// 再弹出下一个节点进行处理root = stack.pop();list.add(root.val);}}}
}
Java解法(统一迭代,中序遍历):
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.inorder(root, ans);return ans;}public void inorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.peek();if(null != root){stack.pop(); // 需要先弹出节点,避免后续重复访问// 节点按照右根左的顺序进栈,后续出栈顺序为左根右(中序遍历)if(null != root.right) stack.push(root.right);stack.push(root);stack.push(null); // 对需要处理的节点,在其后面跟上空指针作为标记if(null != root.left) stack.push(root.left);}else{stack.pop(); // 遇到标记时,先弹出标记// 再弹出下一个节点进行处理root = stack.pop();list.add(root.val);}}}
}
Java解法(统一迭代,后序遍历):
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.postorder(root, ans);return ans;}public void postorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.peek();if(null != root){stack.pop();// 需要先弹出节点,避免后续重复访问// 节点按照根右左的顺序进栈,后续出栈顺序为左右根(后序遍历)stack.push(root);stack.push(null);// 对需要处理的节点,在其后面跟上空指针作为标记if(null != root.right) stack.push(root.right);if(null != root.left) stack.push(root.left);}else{stack.pop();// 遇到标记时,先弹出标记// 再弹出下一个节点进行处理root = stack.pop();list.add(root.val);}}}
}
二叉树结构也是在编程中常见的数据结构之一,例如堆其实就是一个树结构,以及哈希表中也运用到了红黑树来优化哈希表的存储结构等等。
通过今天的练习,我第一次了解并学习到了二叉树的统一迭代遍历算法,利用标记法来遍历二叉树的方法真的是非常巧妙,同时通过迭代算法的练习,也加深了对递归是如何模拟一个栈,以及递归算法如何转变为迭代算法有了一个初步的思路:
门径初窥书海奥, 欣喜若狂凯歌还。
相关文章:

【代码随想录训练营】【Day14】第六章|二叉树|理论基础|递归遍历|迭代遍历|统一迭代
理论基础 二叉树的定义形式有:节点指针和数组 在数组中,父节点的下标为i,那么其左孩子的下标即i*21,右孩子的下标即为i*22 二叉树的常见遍历形式有:前序遍历、后序遍历、中序遍历和层序遍历 前序遍历:二…...

AXI-Stream 学习笔记
参考 https://wuzhikai.blog.csdn.net/article/details/121326701 https://zhuanlan.zhihu.com/p/152283168 AXI4 介绍 AXI4 是ARM公司提出的一种片内总线,描述了主从设备之间的数据传输方式。主要有AXI4_LITE、AXI4_FULL、AXI4_STREAM三种。 AXI4_LITE࿱…...
【Linux】程序进程地址空间
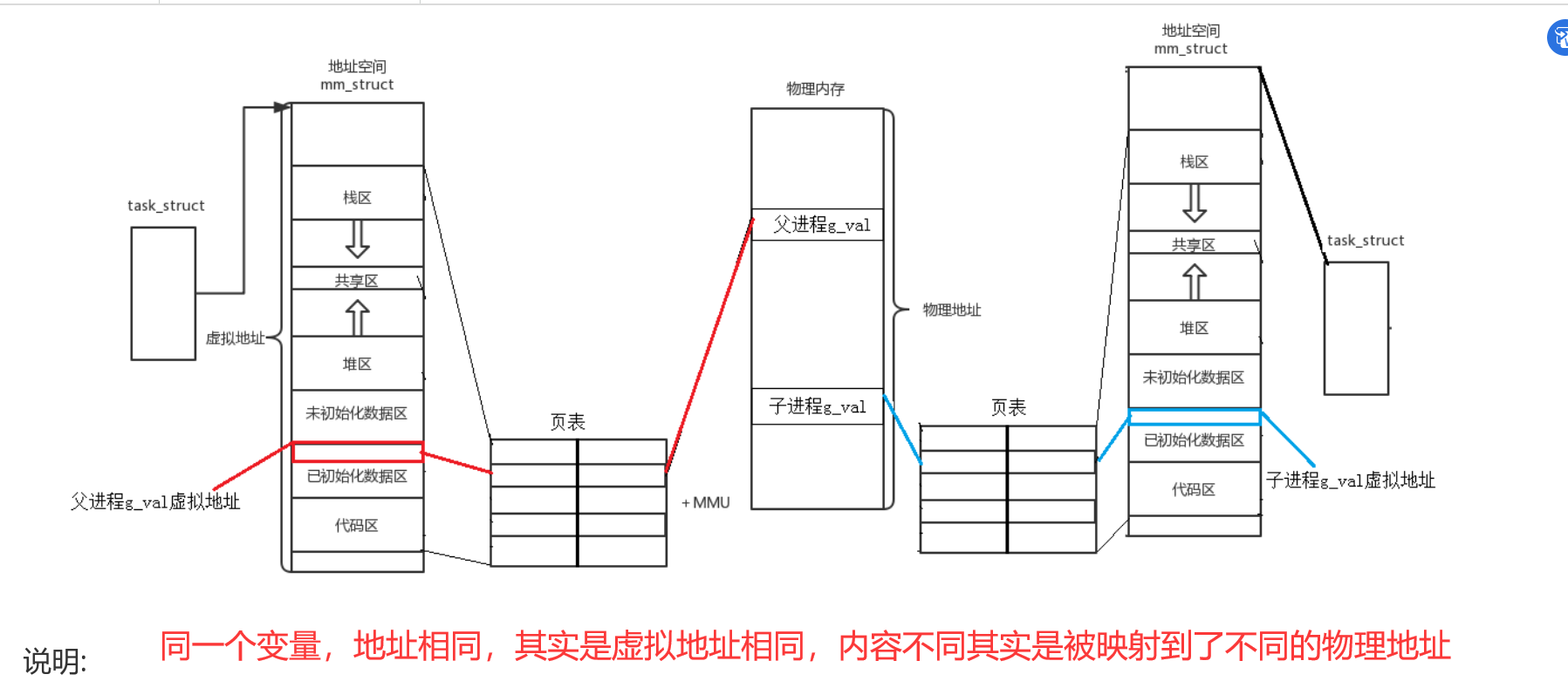
文章目录程序地址空间进程地址空间程序地址空间 在Linux下,这种地址叫做 虚拟地址, 我们在用C/C语言所看到的地址,全部都是虚拟地址!物理地址,用户一概看不到,由OS统一管理 问:C/C程序地址空间是内存吗? -> 根本就不是内存! 是进程虚拟地址空间 堆栈…...

电压放大器在液滴微流控芯片的功能研究中的应用
实验名称:电压放大器在液滴微流控芯片的功能研究中的应用研究方向:微流控生物芯片测试目的:液滴微流控技术能够在微通道内实现液滴生成,精准控制生成液滴的尺寸以及生成频率。结合芯片结构设计和外部控制条件,可以对液…...
Linux操作系统学习(进程地址空间)
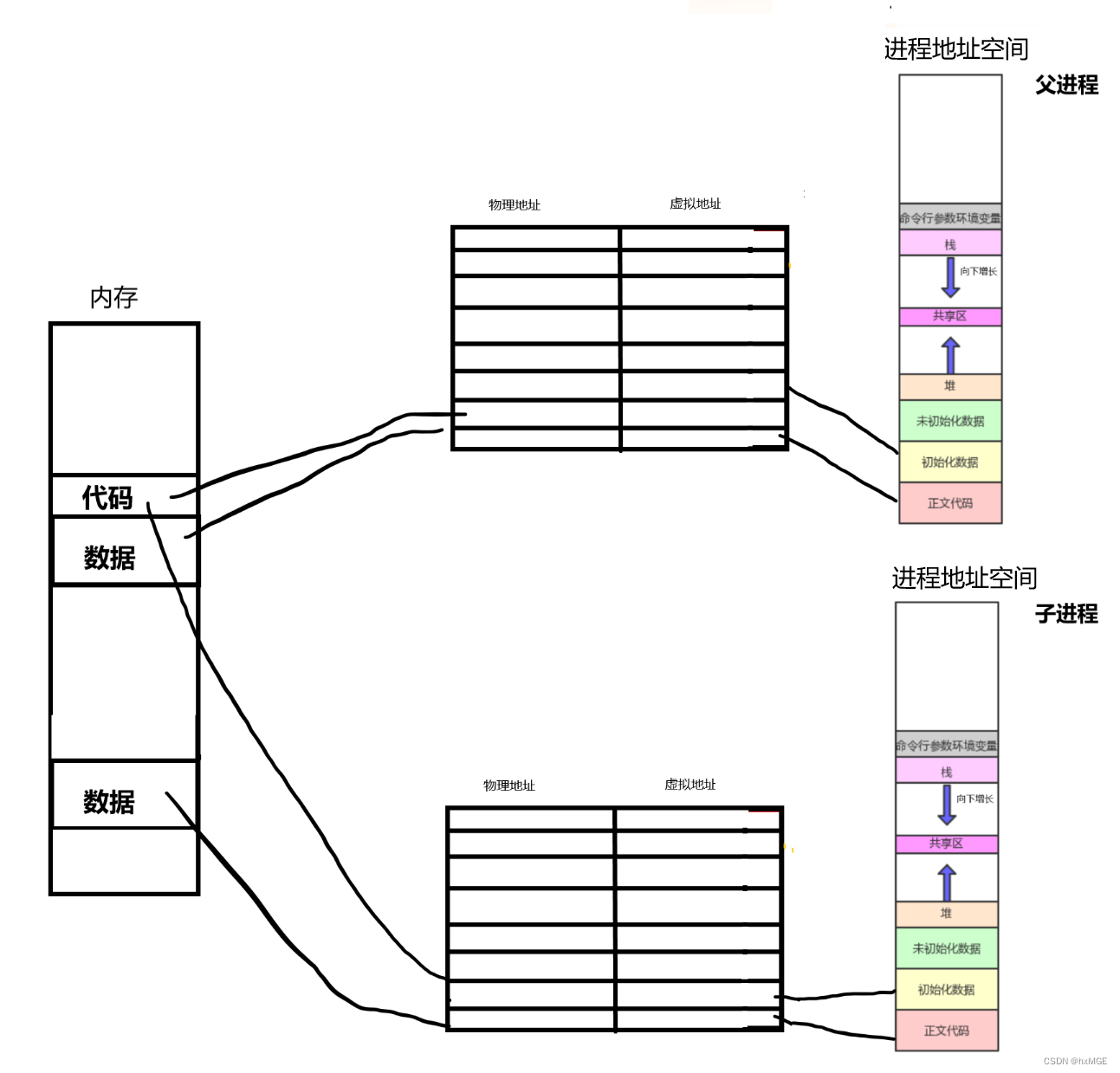
文章目录进程地址空间奇怪的现象什么是进程地址空间???虚拟地址是如何与物理内存联系的?页表是什么呢?为什么要有页表和地址空间,让进程直接访问内存不行吗?现象解释进程地址空间 在我们学习其…...

【排序】快速排序实现
目录 一、快速排序是什么? 二、左右指针法 1.实现原理 2.代码如下: 三、挖坑法 1.实现原理 2.代码如下: 四、前后指针法 1.实现原理 2.代码如下: 五、三数取中 1.实现思想 2.代码如下: 3.使用方法 总结…...

YOLOv5/v7 Flask Web 车牌识别 | YOLOv7 + EasyOCR 实现车牌识别
YOLOv7 Flask Web 车牌识别图片效果展示 本篇博文只包含源码以及使用方式,目前不同提供详细开发教程。 YOLOv7 Flask Web 车牌识别视频效果展示 YOLOv7 + EasyOCR 实现车牌识别 什么是Flask? 简介 Flask是一个轻量级的可定制框架,使用Python语言编写,较其他同类型框架更…...

【Opencv实战】几十年前的Vlog火了:黑白老照片如何上色?这黑科技操作一定要知道,复原度超高,竟美的出奇~(图像修复神级代码)
导语 哈喽大家好呀!我是每天疯狂赶代码的木木子吖~情人节快乐呀! 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末公众hao即可免费。 我们都知道,有很多经典的老照片…...

React源码分析(一)Fiber
前言 本次React源码参考版本为17.0.3。 React架构前世今生 查阅文档了解到, React16.x是个分水岭。 React15及之前 在16之前,React架构大致可以分为两层: Reconciler: 主要职责是对比查找更新前后的变化的组件;R…...
小樽 C++指针—— (壹) 指针变量
(壹) 指针变量 一、指针的概念与定义 二、给指针变量p赋值 三、指针变量的的、-运算 四、无类型指针 五、多重指针 C (壹) 指针变量 小明想把从李华家借来的书——《CCF中学生计算机程序设计》还给李华,但李华不在家,于是把书放到书架第3层的最右边…...
java 代码块 万字详解
概述 : 特点 : 格式 : 情景 : 细节 : 演示 : 英文 : //v,新版编辑器无手动添加目录的功能,PC端阅读建议通过侧边栏进行目录跳转;移动端建议用PC端阅读。😂一、概述 :代码块,也称为初始化块,属于类中的成员&…...
杂项-图片隐写
图片隐写的常见隐写方法: 三基色:RGB(Red Green Blue) 图片文件隐写 1.Firework 使用winhex打开文件时会看到文件头部中包含firework的标识,通过firework可以找到隐藏图片。 使用场景:查看隐写的图片文件…...

【高性价比】初学者入门吉他值得推荐购买的民谣单板吉他品牌—VEAZEN费森吉他
“在未知的世界里,我们是一群不疲不倦的行者,执念于真善美,热衷于事物的极致。我们抽丝剥茧,不断地打败自己,超越自己,我们无所畏惧终将成为巨人。”这是VEAZEN吉他官网首页上很明显的一段话,也…...
2023年浙江交安安全员考试题库及答案
百分百题库提供交安安全员考试试题、交安安全员考试真题、交安安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 50.根据《建设工程安全生产管理条例》第65条规定,施工单位有下列()行…...
)
【新】华为OD机试 - 跳格子(Python)
跳格子 题目 地上共有 N 个格子,你需要跳完地上所有的格子, 但是格子间是有强依赖关系的,跳完前一个格子后, 后续的格子才会被开启,格子间的依赖关系由多组 steps 数组给出, steps[0] 表示前一个格子, steps[1] 表示 steps[0] 可以开启的格子: 比如 [0,1] 表示从跳完第…...

乡村能做社区团购吗?怎么做?我走访调查后发现机会很大
乡村能做社区团购吗?怎么做?我走访调查后发现机会很大#深度触网 #社区团购 #乡村振兴##乡村旅游##县域经济##市场经济##农文旅产业振兴研究院#乡村旅游能带动农产品加工业、服务业、商贸业等相关联产业的发展 乡村能做社区团购吗?怎么做&…...

态路小课堂丨下一代数据中心100G接口第二篇——SFP-DD封装
100G光模块根据封装模式可分为QSFP28、CXP、CFP、CFP2、FCP4、DSFP和SFP-DD等。态路小课堂之前已经大量介绍了相关内容(。 态路小课堂丨下一代数据中心100G接口——DSFP态路小课堂丨100G解决方案-425G NRZ光模块态路小课堂丨什么是100G QSFP28单波光模块?…...

状态栏和导航栏高度获取
/*** 获取导航栏高度*/public static int getNavigationBarHeight(Context context){int navigationBarHeight 0;int resourceId context.getResources().getIdentifier("navigation_bar_height", "dimen", "android")if (resourceId > 0) {…...

插曲:第一桶金 1w 的来由
因为前天跟同事聊天,发现有个比较严重的认知,就是关于赚钱思维。 同事反馈说工作十来年,却没有接过私活,这里话分两头,有可能私 活钱少,但他给我的理由是:私活太麻烦,有时候不敢接&a…...

中国甲基异丁基甲醇行业头部企业市场占有率及排名调研报告
内容摘要 本文调研和分析全球甲基异丁基甲醇发展现状及未来趋势,核心内容如下: (1)全球市场总体规模,分别按销量和按收入进行了统计分析,历史数据2018-2022年,预测数据2023至2029年。 …...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
