对抗生成网络GAN系列——Spectral Normalization原理详解及源码解析
🍊作者简介:秃头小苏,致力于用最通俗的语言描述问题
🍊专栏推荐:深度学习网络原理与实战
🍊近期目标:写好专栏的每一篇文章
🍊支持小苏:点赞👍🏼、收藏⭐、留言📩
对抗生成网络GAN系列——Spectral Normalization原理详解及源码解析
写在前面
Hello,大家好,我是小苏🧒🏽🧒🏽🧒🏽
在前面的文章中,我已经介绍过挺多种GAN网络了,感兴趣的可以关注一下我的专栏:深度学习网络原理与实战 。目前专栏主要更新了GAN系列文章、Transformer系列和语义分割系列文章,都有理论详解和代码实战,文中的讲解都比较通俗易懂,如果你希望丰富这方面的知识,建议你阅读试试,相信你会有蛮不错的收获。🍸🍸🍸
在阅读本篇教程之前,你非常有必要阅读下面两篇文章:
- [1]对抗生成网络GAN系列——DCGAN简介及人脸图像生成案例
- [2]对抗生成网络GAN系列——WGAN原理及实战演练
其实啊,我相信大家来看这篇文章的时候,一定是对上文提到的文章有所了解了,因此大家要是觉得自己对GAN和WGAN了解的已经足够透彻了,那么完全没有必要再浪费时间阅读了。如果你还对它们有一些疑惑或者过了很久已经忘了希望回顾一下的话,那么文章[1]和文章[2]获取对你有所帮助。
大家准备好了嘛,我们这就开始准备学习Spectral Normalization啦!🚖🚖🚖
Spectral Normalization原理详解
首先,让我们简单的回顾一下WGAN。🌞🌞🌞由于原始GAN网络存在训练不稳定的现象,究其本质,是因为它的损失函数实际上是JS散度,而JS散度不会随着两个分布的距离改变而改变(这句不严谨,细节参考WGAN中的描述),这就会导致生成器的梯度会一直不变,从而导致模型训练效果很差。WGAN为了解决原始GAN网络训练不稳定的现象,引入了EM distance代替原有的JS散度,这样的改变会使生成器梯度一直变化,从而使模型得到充分训练。但是WGAN的提出伴随着一个难点,即如何让判别器的参数矩阵满足Lipschitz连续条件。
如何解决上述所说的难点呢?在WGAN中,我们采用了一种简单粗暴的方式来满足这一条件,即直接对判别器的权重参数进行剪裁,强制将权重限制在[-c,c]范围内。大家可以动动我们的小脑瓜想想这种权重剪裁的方式有什么样的问题——(滴,揭晓答案🍍🍍🍍)如果权重剪裁的参数c很大,那么任何权重可能都需要很长时间才能达到极限,从而使训练判别器达到最优变得更加困难;如果权重剪裁的参数c很小,这又容易导致梯度消失。因此,如何确定权重剪裁参数c是重要的,同时这也是困难的。WGAN提出之后,又提出了WGAN-GP来实现Lipschitz 连续条件,其主要通过添加一个惩罚项来实现。【关于WGAN-GP我没有做相关教程,如果不明白的可以评论区留言】那么本文提出了一种归一化的手段Spectral Normalization来实现Lipschitz连续条件,这种归一化具体是怎么实现的呢,下面听我慢慢道来。🍻🍻🍻
我们还是来先回顾一下Lipschitz连续条件,如下:
∣f(x1)−f(x2)∣≤K∣x1−x2∣|f(x_1)-f(x_2)| \le K|x_1-x_2|∣f(x1)−f(x2)∣≤K∣x1−x2∣
这个式子限制了函数f(⋅){\rm{f}}( \cdot )f(⋅)的导数,即其导数的绝对值小于K,∣f(x1)−f(x2)∣∣x1−x2∣≤K\frac{|f(x_1)-f(x_2)|}{|x_1-x_2|} \le K∣x1−x2∣∣f(x1)−f(x2)∣≤K。 🍋🍋🍋
本文介绍的Spectral Normalization的K=1,让我们一起来看看怎么实现的吧!!!
上文提到,WGAN的难点是如何让判别器的参数矩阵满足Lipschitz连续条件。那么我们就从判别器入手和大家唠一唠。实际上,判别器也是由多层卷积神经网络构成的,我们用下式表示第n层网络输出和第n-1层输入的关系:
Xn=an(Wn⋅Xn−1+bn)X_n=a_n(W_n \cdot X_{n-1}+b_n)Xn=an(Wn⋅Xn−1+bn)
其中an(⋅)a_n(\cdot)an(⋅)表示激活函数,WnW_nWn表示权重参数矩阵。为了方便起见,我们不设置偏置项bnb_nbn,即bn=0b_n=0bn=0。那么上式变为:
Xn=an(Wn⋅Xn−1)X_n=a_n(W_n \cdot X_{n-1})Xn=an(Wn⋅Xn−1)
再为了方便起见🤸🏽♂️🤸🏽♂️🤸🏽♂️,我们设an(⋅)a_n(\cdot)an(⋅),即激活函数为Relu。Relu函数在大于0时为y=x,小于0时为y=0,函数图像如下图所示:
这样的话式Xn=an(Wn⋅Xn−1)X_n=a_n(W_n \cdot X_{n-1})Xn=an(Wn⋅Xn−1)可以写成Xn=Dn⋅Wn⋅Xn−1X_n=D_n \cdot W_n \cdot X_{n-1}Xn=Dn⋅Wn⋅Xn−1,其中DnD_nDn为对角矩阵。【大家这里能否理解呢?如果我们的输入为正数时,通过Relu函数值是不变的,那么此时DnD_nDn对应的对角元素应该为1;如果我们的输入为负数时,通过Relu函数值将变成0,那么此时DnD_nDn对应的对角元素应该为0。也就是说我们将XnX_nXn改写成Dn⋅Wn⋅Xn−1D_n \cdot W_n \cdot X_{n-1}Dn⋅Wn⋅Xn−1形式是可行的。】
接着我们做一些简单的推理,得到判别器第n层输出和原始输入的关系,如下图所示:

最后一层的输出XnX_nXn即为判别器的输出,接下来我们用f(x)f(x)f(x)表示;原始输入数据x0x_0x0我们接下来用xxx表示。则判别器最终输入输出的关系式如下:
f(x)=Dn⋅Wn⋅Dn−1⋅Wn−1⋯D3⋅W3⋅D2⋅W2⋅D1⋅W1⋅xf(x) = {D_n} \cdot {W_n} \cdot {D_{n - 1}} \cdot {W_{n - 1}} \cdots {D_3} \cdot {W_3} \cdot {D_2} \cdot {W_2} \cdot {D_1} \cdot {W_1} \cdot xf(x)=Dn⋅Wn⋅Dn−1⋅Wn−1⋯D3⋅W3⋅D2⋅W2⋅D1⋅W1⋅x
上文说到Lipschitz连续条件本质上就是限制函数f(⋅){\rm{f}}( \cdot )f(⋅)的导数变化范围,其实就是对f(x)f(x)f(x)梯度提出限制,如下:
∣∣∇xf(x)∣∣2=∣∣Dn⋅Wn⋅Dn−1⋅Wn−1⋯D3⋅W3⋅D2⋅W2⋅D1⋅W1∣∣2≤∣∣Dn∣∣2⋅∣∣Wn∣∣2⋅∣∣Dn−1∣∣2⋅∣∣Wn−1∣∣2⋯∣∣D1∣∣2⋅∣∣W1∣∣2||{\nabla _x}f(x)|{|_2} = ||{D_n} \cdot {W_n} \cdot {D_{n - 1}} \cdot {W_{n - 1}} \cdots {D_3} \cdot {W_3} \cdot {D_2} \cdot {W_2} \cdot {D_1} \cdot {W_1}|{|_2} \le ||{D_n}|{|_2} \cdot ||{W_n}|{|_2} \cdot ||{D_{n - 1}}|{|_2} \cdot ||{W_{n - 1}}|{|_2} \cdots ||{D_1}|{|_2} \cdot ||{W_1}|{|_2}∣∣∇xf(x)∣∣2=∣∣Dn⋅Wn⋅Dn−1⋅Wn−1⋯D3⋅W3⋅D2⋅W2⋅D1⋅W1∣∣2≤∣∣Dn∣∣2⋅∣∣Wn∣∣2⋅∣∣Dn−1∣∣2⋅∣∣Wn−1∣∣2⋯∣∣D1∣∣2⋅∣∣W1∣∣2
其中∣∣A∣∣2||A||_2∣∣A∣∣2表示矩阵A的2范数,也叫谱范数,它的值为λ1\sqrt {{\lambda _1}}λ1,λ1{\lambda _1}λ1为 AHA{{\rm{A}}^H}{\rm{A}}AHA的最大特征值。λ1\sqrt {{\lambda _1}}λ1又称作矩阵A的奇异值【注:奇异值是AHA{{\rm{A}}^H}{\rm{A}}AHA的特征值的开根号,也就是说λ1\sqrt {{\lambda _1}}λ1为A的其中一个奇异值或谱范数是最大的奇异值,这里我们将谱范数,即最大的奇异值记作σ(A)=λ1\sigma {(A)} = \sqrt {{\lambda _1}}σ(A)=λ1。由于D是对角矩阵且由0、1构成,其奇异值总是小于等于1,故有下式:

即∇xf(x)∣∣2=∣∣Dn∣∣2⋅∣∣Wn∣∣2⋯∣∣D1∣∣2⋅∣∣W1∣∣2≤Π1nσ(Wi){\nabla _x}f(x)|{|_2}= ||{D_n}|{|_2}\cdot ||{W_n}|{|_2} \cdots ||{D_1}|{|_2} \cdot ||{W_1}|{|_2} \le \mathop \Pi \limits_1^{\rm{n}} \sigma ({W_i})∇xf(x)∣∣2=∣∣Dn∣∣2⋅∣∣Wn∣∣2⋯∣∣D1∣∣2⋅∣∣W1∣∣2≤1Πnσ(Wi)。为满足Lipschitz连续条件,我们应该让∣∣∇xf(x)∣∣2≤K||{\nabla _x}f(x)|{|_2} \le K∣∣∇xf(x)∣∣2≤K ,这里的K设置为1。那具体要怎么做呢,其实就是对上式做一个归一化处理,让每一层参数矩阵除以该层参数矩阵的谱范数,如下:
∣∣∇xf(x)∣∣2=∣Dn∣∣2⋅∣∣Wn∣∣2σ(Wn)⋯∣∣D1∣∣2⋅∣∣W1∣∣2σ(W1)≤Π1nσ(Wi)σ(Wi)=1||{\nabla _x}f(x)|{|_2} = |{D_n}|{|_2} \cdot \frac{{||{W_n}|{|_2}}}{{\sigma ({W_n})}} \cdots ||{D_1}|{|_2} \cdot \frac{{||{W_1}|{|_2}}}{{\sigma ({W_1})}} \le \mathop \Pi \limits_1^{\rm{n}} \frac{{\sigma ({W_i})}}{{\sigma ({W_i})}} = 1∣∣∇xf(x)∣∣2=∣Dn∣∣2⋅σ(Wn)∣∣Wn∣∣2⋯∣∣D1∣∣2⋅σ(W1)∣∣W1∣∣2≤1Πnσ(Wi)σ(Wi)=1
这样,其实我们的Spectral Normalization原理就讲的差不多了,最后我们要做的就是求得每层参数矩阵的谱范数,然后再进行归一化操作。要想求矩阵的谱范数,首先得求矩阵的奇异值,具体求法我放在附录部分。
但是按照正常求奇异值的方法会消耗大量的计算资源,因此论文中使用了一种近似求解谱范数的方法,伪代码如下图所示:

在代码的实战中我们就是按照上图的伪代码求解谱范数的,届时我们会为大家介绍。🍄🍄🍄
注:大家阅读这部分有没有什么难度呢,我觉得可能还是挺难的,你需要一些矩阵分析的知识,我已经尽可能把这个问题描述的简单了,有的文章写的很好,公式推导的也很详尽,我会在参考链接中给出。但是会涉及到最优化的一些理论,估计这就让大家更头疼了,所以大家慢慢消化吧!!!🍚🍚🍚在最后的附录中,我会给出本节内容相关的矩阵分析知识,是我上课时的一些笔记,笔记包含本节的知识点,但针对性可能不是很强,也就是说可能包含一些其它内容,大家可以选择忽略,当然了,你也可以细细的研究研究每个知识点,说不定后面就用到了呢!!!🥝🥝🥝
Spectral Normalization源码解析
源码下载地址:Spectral Normalization📥📥📥
这个代码使用的是CIFAR10数据集,实现的是一般生成对抗网络的图像生成任务。我不打算再对每一句代码进行详细的解释,有不明白的可以先去看看我专栏中的其它GAN网络的文章,都有源码解析,弄明白后再看这篇你会发现非常简单。那么这篇文章我主要来介绍一下Spectral Normalization部分的内容,其相关内容在spectral_normalization.py文件中,我们理论部分提到Spectral Normalization关键的一步是求解每个参数矩阵的谱范数,相关代码如下:
def _update_u_v(self):u = getattr(self.module, self.name + "_u")v = getattr(self.module, self.name + "_v")w = getattr(self.module, self.name + "_bar")height = w.data.shape[0]for _ in range(self.power_iterations):u.data = l2normalize(torch.mv(w.view(height, -1).data, v.data)) v.data = l2normalize(torch.mv(torch.t(w.view(height,-1).data), u.data))sigma = u.dot(w.view(height, -1).mv(v))setattr(self.module, self.name, w / sigma.expand_as(w))def l2normalize(v, eps=1e-12):return v / (v.norm() + eps)
对上述代码做一定的解释,6,7,8,9,10行做的就是理论部分伪代码的工作,最后会得到谱范数sigma。11行为使用参数矩阵除以谱范数sigma,以此实现归一化的作用。【torch.mv实现的是矩阵乘法的操作,里面可能还有些函数你没见过,大家百度一下用法就知道了,非常简单】
其实关键的代码就这些,是不是发现特别简单呢🍸🍸🍸每次介绍代码时我都会强调自己动手调试的重要性,很多时候写文章介绍源码都觉得有些力不从心,一些想表达的点总是很难表述,总之,大家要是有什么不明白的就尽情调试叭,或者评论区留言,我天天在线摸鱼滴喔。⭐⭐⭐后期我也打算出一些视频教学了,这样的话就可以带着大家一起调试,我想这样介绍源码彼此都会轻松很多。🛩🛩🛩
小结
Spectral Normalization确实是有一定难度的,我也有许多地方理解的也不是很清楚,对于这种难啃的问题我是这样认为的。我们可以先对其有一个大致的了解,知道整个过程,知道代码怎么实现,能使用代码跑通一些模型,然后考虑能否将其用在自己可能需要使用的地方,如果加入的效果不好,我们就没必要深究原理了,如果发现效果好,这时候我们再回来慢慢细嚼原理也不迟。最后,希望各位都能获取新知识,能够学有所成叭!!!🌹🌹🌹
参考链接
GAN — Spectral Normalization 🍁🍁🍁
Spectral Normalization for GAN🍁🍁🍁
详解GAN的谱归一化(Spectral Normalization)🍁🍁🍁
谱归一化(Spectral Normalization)的理解🍁🍁🍁
附录
这部分是我学习矩阵分析这门课程时的笔记,截取一些包含此部分的内容,有需求的感兴趣的可以看一看。🌱🌱🌱




如若文章对你有所帮助,那就🛴🛴🛴

相关文章:

对抗生成网络GAN系列——Spectral Normalization原理详解及源码解析
🍊作者简介:秃头小苏,致力于用最通俗的语言描述问题 🍊专栏推荐:深度学习网络原理与实战 🍊近期目标:写好专栏的每一篇文章 🍊支持小苏:点赞👍🏼、…...

Solon2 开发之插件,一、插件
Solon Plugin 是框架的核心接口,简称“插件”。其本质是一个“生命周期”接口。它可让一个组件类参与程序的生命周期过程(这块看下:《应用启动过程与完整生命周期》): FunctionalInterface public interface Plugin {…...
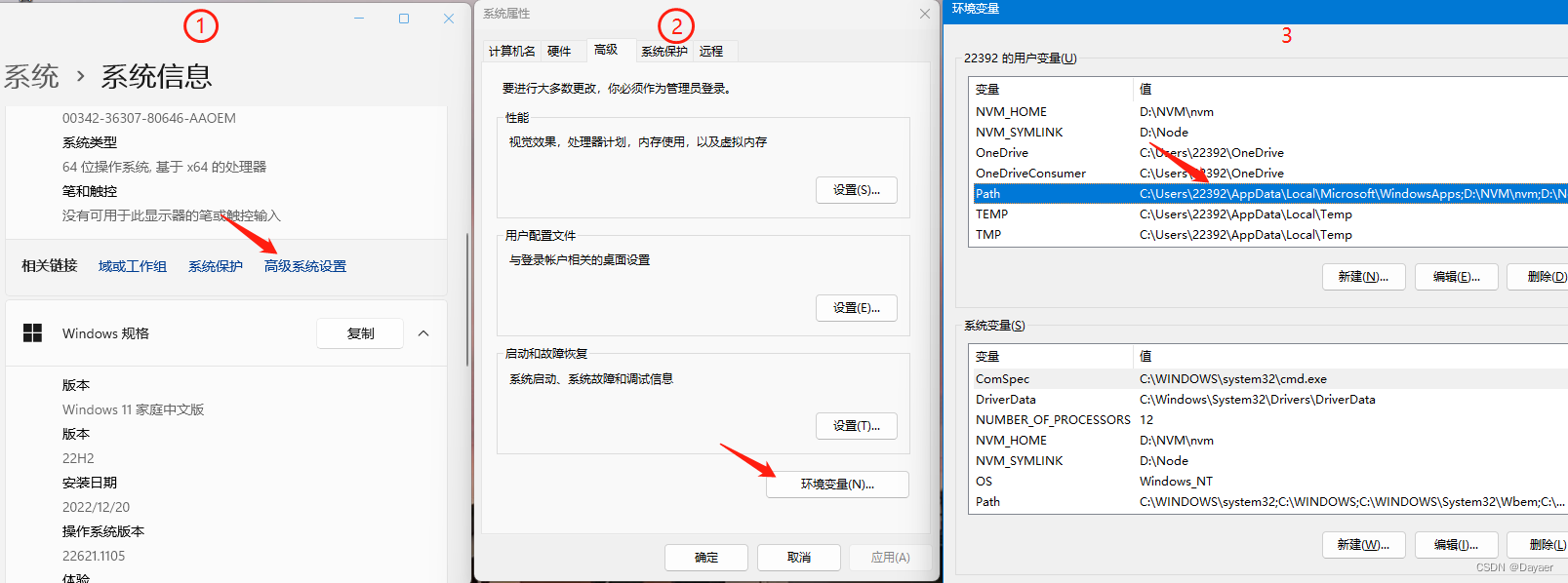
使用nvm管理node
nvm介紹 node的版本管理器,可以方便地安装&切换不同版本的node 我们在工作中,可以会有老版本的node的项目需要维护,也可能有新版本的node的项目需要开发,如果只有一个node版本的话将会很麻烦,nvm可以解决我们的难点…...

Linux
第一章 Linux 1.1 计算机硬件软件体系 冯诺依曼 (数学家,计算机之父) 冯诺依曼体系 计算机的指令和数据都是二进制存储,并且存放到一起程序和指令都是顺序执行的计算机硬件由输入,输出,存储,运算器与控制器组成 输入设备 比如:键盘,鼠标等. 输出设备 打印机输出࿰…...
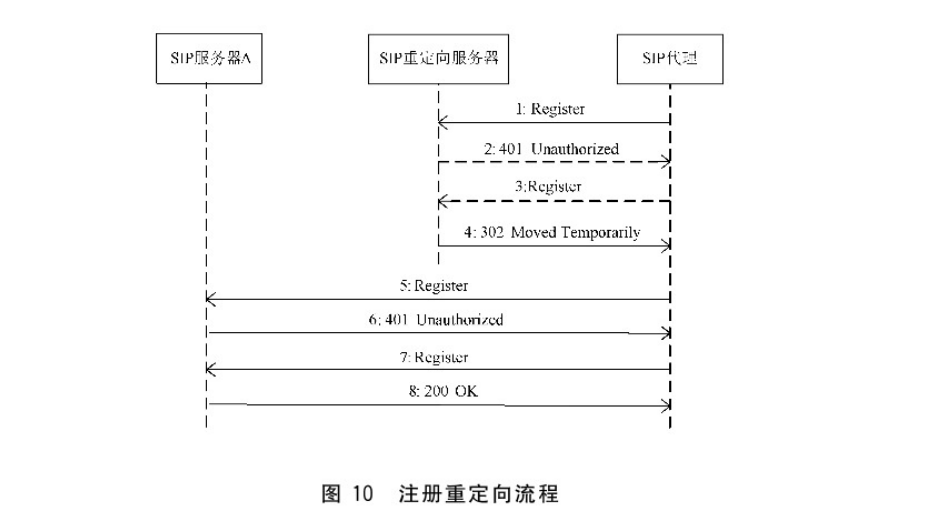
GB28181-2022注册注销基本要求、注册重定向解读和技术实现
规范解读GB28181-2022注册、注销基本要求相对GB28181-2016版本,做了一定的调整,新调整的部分如下:——更改了注册和注销基本要求(见 9.1.1,2016 年版的 9.1.1)。1.增加对NAT模式网络传输要求,宜…...

2023年二建报考条件是什么?考试考什么?来考网
2023年二建报考条件是什么?考试考什么?来考网 2023年二建报考条件是什么?考试考什么?来考网 二建报考条件: 1、中专及以上学历 2、工程或工程经济类专业 3、从事施工管理工作满2年 二建考试科目: 《建设工…...
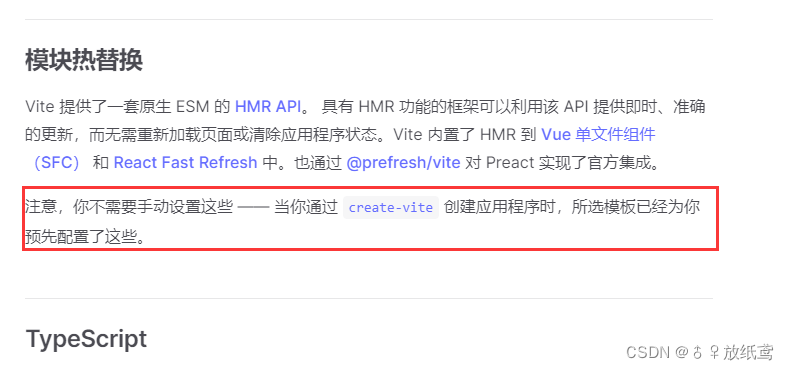
vite+vue3搭建的工程热更新失效问题
前段时间开发新的项目,由于没有技术上的限制,所以选择了vitevue3ts来开发新的项目,一开始用vite来开发新项目过程挺顺利,确实比vue2webpack的项目高效些(为什么选择vite),但是过了一段时间后,不…...
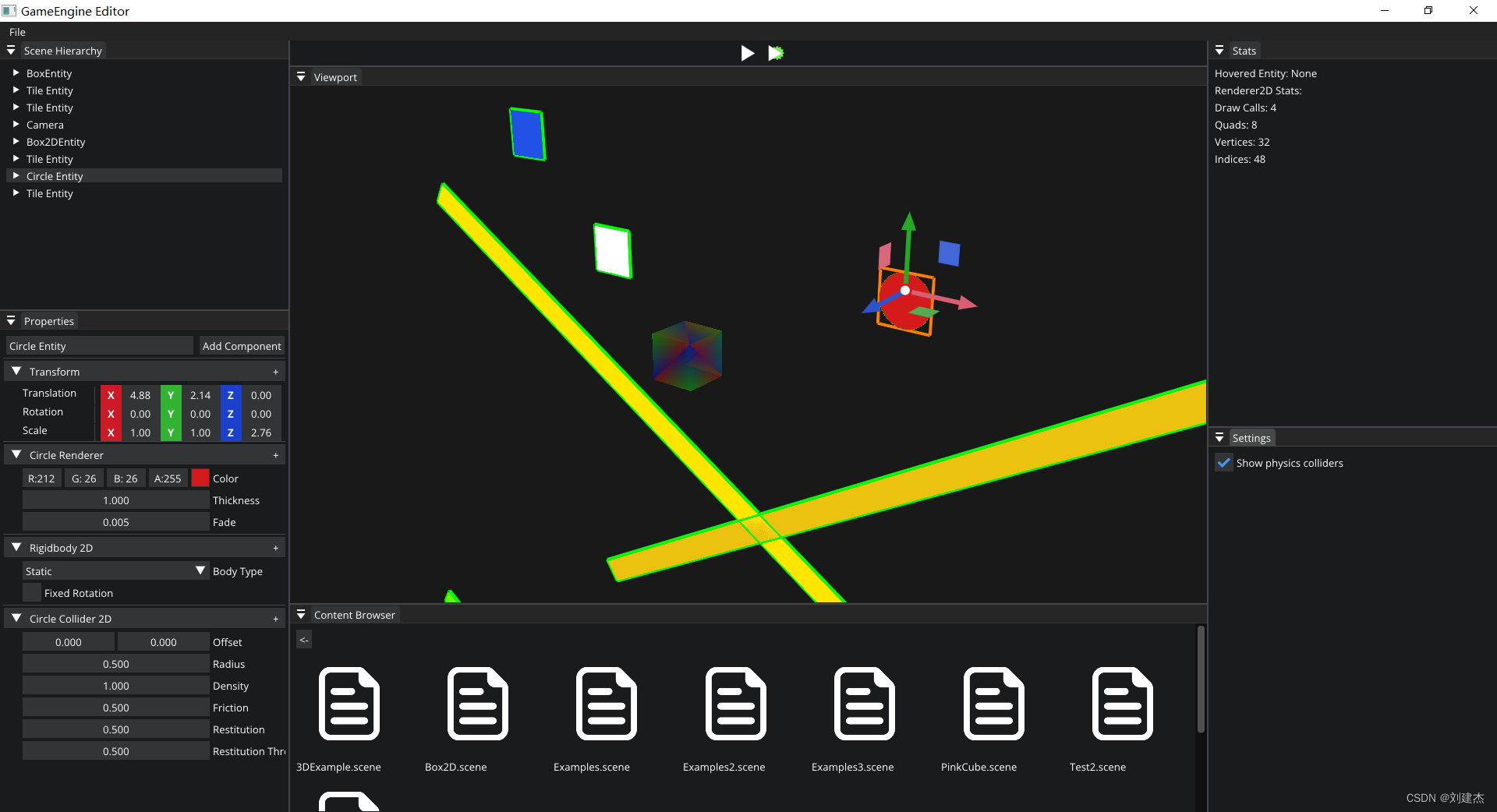
Hazel游戏引擎(001-003)
文章目录前言001.游戏引擎介绍002.什么是游戏引擎003设计我们的游戏引擎本人菜鸟,文中若有代码、术语等错误,欢迎指正 前言 我写的项目地址 https://github.com/liujianjie/GameEngineLightWeight(中文的注释适合中国人的你) 关于…...

耗时一个星期整理的APP自动化测试工具大全
在本篇文章中,将给大家推荐14款日常工作中经常用到的测试开发工具神器,涵盖了自动化测试、APP性能测试、稳定性测试、抓包工具等。 一、UI自动化测试工具 1. uiautomator2 openatx开源的ui自动化工具,支持Android和iOS。主要面向的编程语言…...
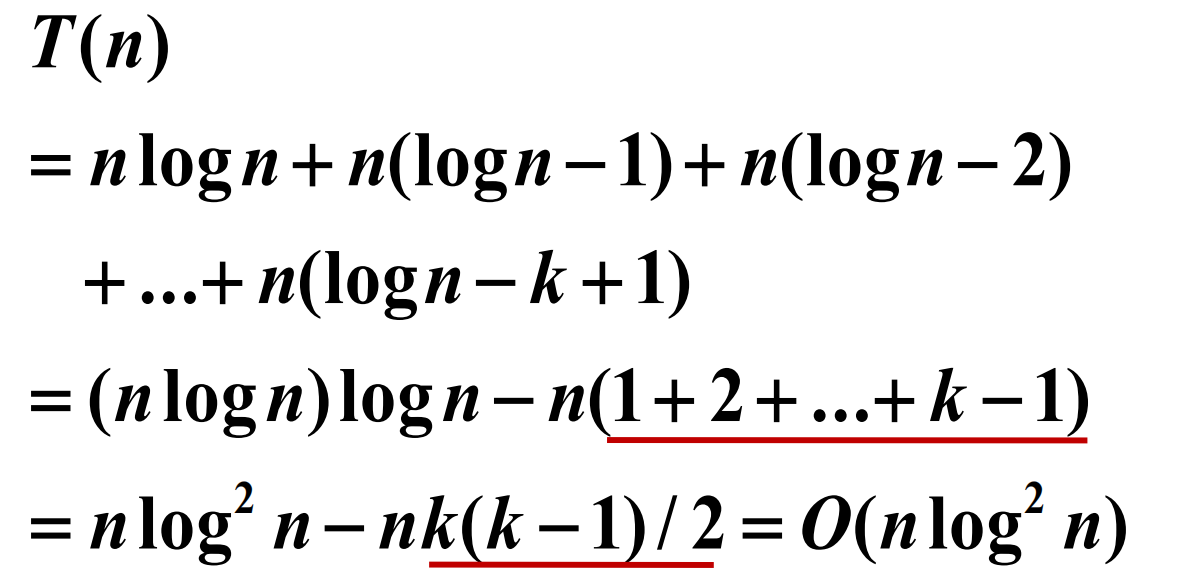
算法设计与分析(屈婉玲)视频笔记day2
序列求和的方法 数列求和公式 等差、等比数列与调和级数 求和的例子 二分检索算法 二分检索运行实例 2 n 1个输入 比较 t 次的输入个数 二分检索平均时间复杂度 估计和式上界的放大法 放大法的例子 估计和式渐近的界 估计和式渐近的界 小结 • 序列求和基本公式:…...

14-PHP使用过的函数 131-140
131、session_unset 释放当前会话注册的所有会话变量。 没有返回值。 132、session_destroy 销毁当前会话中的全部数据, 但是不会重置当前会话所关联的全局变量, 也不会重置会话 cookie。 如果需要再次使用会话变量, 必须重新调用 session_…...

【第39天】实现一个冒泡排序
本文已收录于专栏 🌸《Java入门一百例》🌸 学习指引 序、专栏前言一、冒泡排序一、【例题1】1、题目描述2、解题思路3、模板代码三、推荐专栏序、专栏前言 本专栏开启,目的在于帮助大家更好的掌握学习Java,特别是一些Java学习者难以在网上找到系统地算法学习资料帮助自身…...

「2」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 方阵的行列式 (1) |A^T||A|(2) |ǖ…...

动态规划专题——背包问题
🧑💻 文章作者:Iareges 🔗 博客主页:https://blog.csdn.net/raelum ⚠️ 转载请注明出处 目录前言一、01背包1.1 使用滚动数组优化二、完全背包2.1 使用滚动数组优化三、多重背包3.1 使用二进制优化四、分组背包总结…...

数据的分组聚合
1:分组 t.groupby #coding:utf-8 import pandas as pd import numpy as np file_path./starbucks_store_worldwide.csv dfpd.read_csv(file_path) #print(df.head(1)) #print(df.info()) groupeddf.groupby(byCountry) print(grouped) #DataFrameGroupBy #可以遍历…...
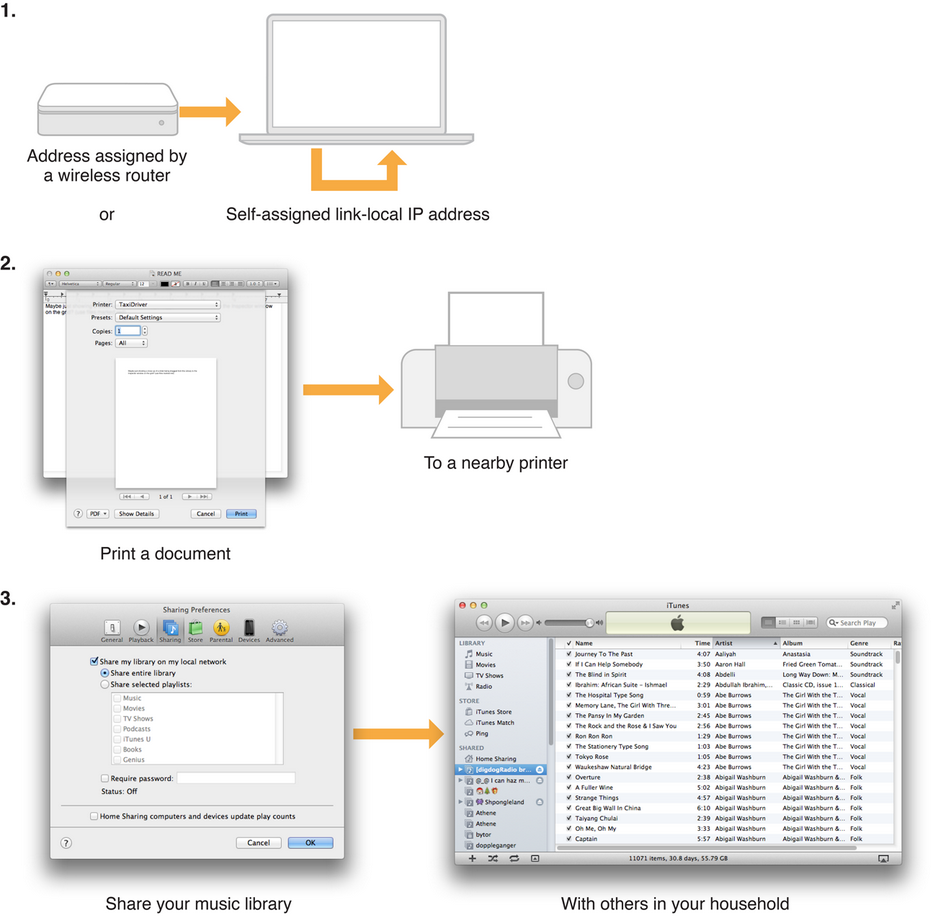
【Airplay_BCT】Bonjour conformance tests苹果IOT
从Airplay开始,接触到BCT,这是什么?被迫从安卓变成ios用户和开发。。。开始我的学习之旅,记录成长过程,不定时更新 Bonjour 下面是苹果官网关于bonjour的解释 Bonjour, also known as zero-configuration networking, …...
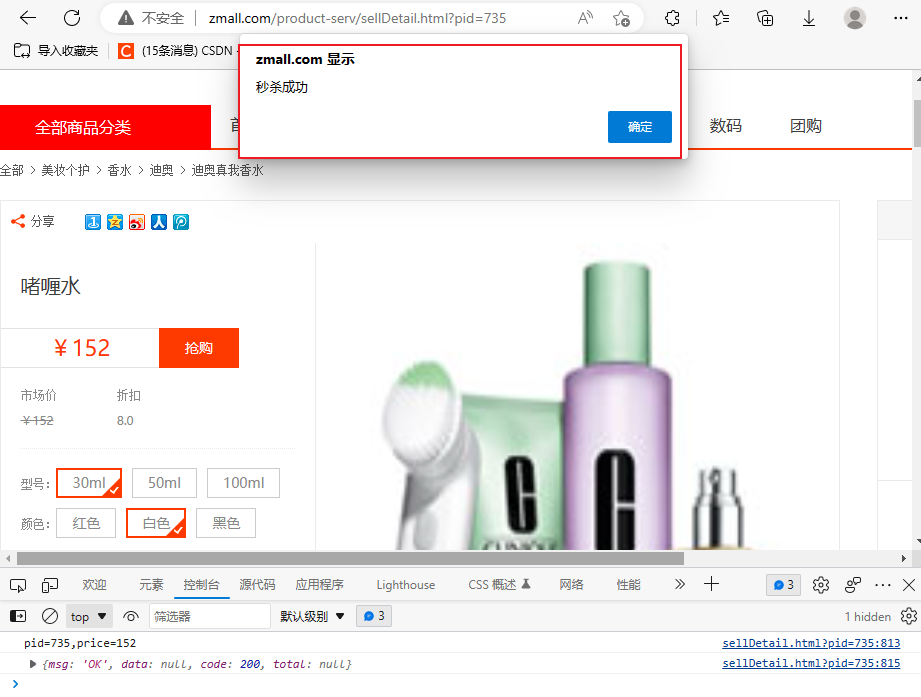
开发微服务电商项目演示(五)
登录方式调整第1步:从zmall-common的pom.xml中移除spring-session-data-redis依赖注意:本章节中不采用spring-session方式,改用redis直接存储用户登录信息,主要是为了方便之后的jmeter压测;2)这里只注释调用…...

Git删除大文件历史记录
Git删除大文件历史记录 git clone 仓库地址 查看大文件并排序 git rev-list --objects --all |grep $(git verify-pack -v .git/objects/pack/pack-*.idx | sort -k 3 -g | tail -1|awk {print $1})删除大文件 git filter-branch --force --index-filter git rm --cached --ig…...
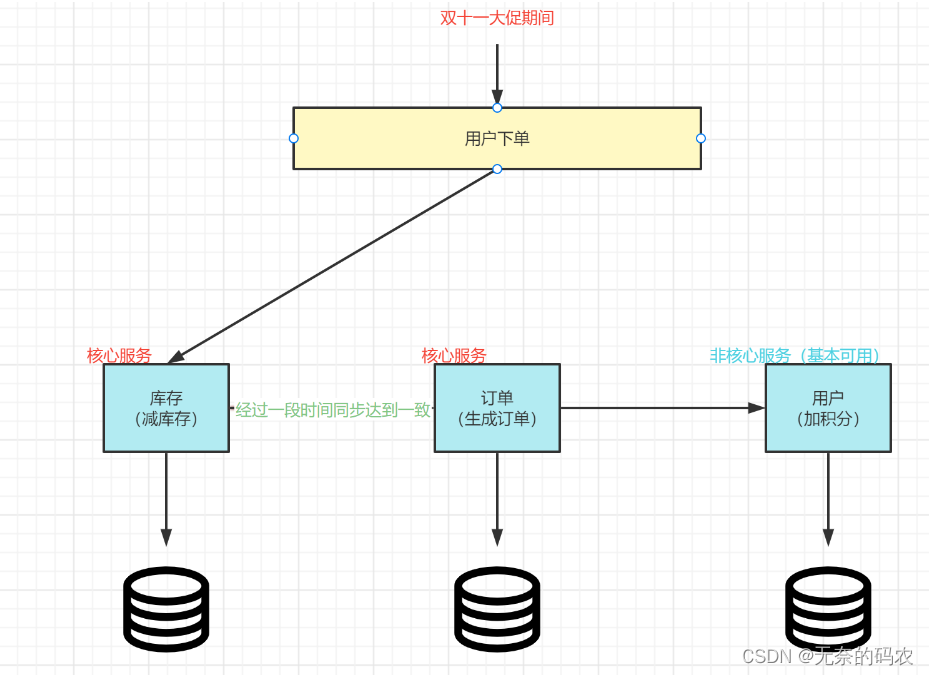
Seata-Server分布式事务原理加源码(一) - 微服务之分布式事务原理
概念 基础概念:事务ACID • A(Atomic):原子性,构成事务的所有操作,要么都执行完成,要么全部不执行,不可能出现部分成功部分失 败的情况。 • C(Consistency)…...

【ZooKeeper】zookeeper源码9-ZooKeeper读写流程源码分析
源码项目zookeeper-3.6.3:核心工作流程ZooKeeper选举和状态同步结束之后的服务启动ZooKeeper SessionTracker启动和工作机制ZooKeeper选举和状态同步结束之后的服务启动 在Leader的lead()方法的最后,即Leader完成了和集群过半Follower的同步之后&#x…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
