「3」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
矩阵的秩
第四章 向量组的线性相关性
向量组及其线性组合
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸
相关文章:
)
「3」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 矩阵的秩 定义4:在mxn矩阵A中,任取k行与k列(k<m,k<n),位…...
)
【CSDN竞赛】27期题解(Javascript)
前言 本来排名是20的,不过第一题有点输出bug,最后实际测出来又重新排名,刚好卡在第10。但是考试报告好像过了12小时就下载不到了,所以就只写题目求解的JS函数吧。 1. 幸运数字 小艺定义一个幸运数字的标准包含3条: 仅包含4或7幸…...

高压放大器在骨的逆力电研究中的应用
实验名称:高压放大器在骨的逆力电研究中的应用研究方向:生物医学测试目的:骨中的胶原和羟基磷灰石沿厚度分布不均匀,骨试样在直流电压作用下,内部出现传导电流引起试样内部温度升高,不同组分热变形不一致&a…...
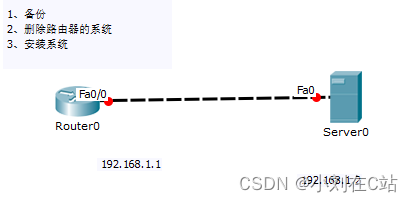
思科网络部署,(0基础)入门实验,超详细
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...
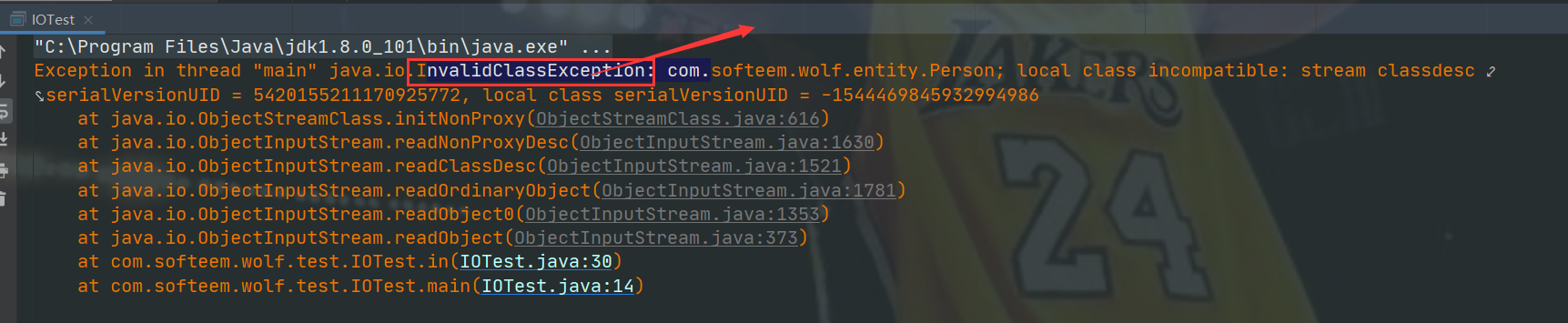
private static final Long serialVersionUID= 1L详解
我们知道在对数据进行传输时,需要将其进行序列化,在Java中实现序列化的方式也很简单,可以直接通过实现Serializable接口。但是我们经常也会看到下面接这一行代码,private static final Long serialVersionUID 1L;这段代…...
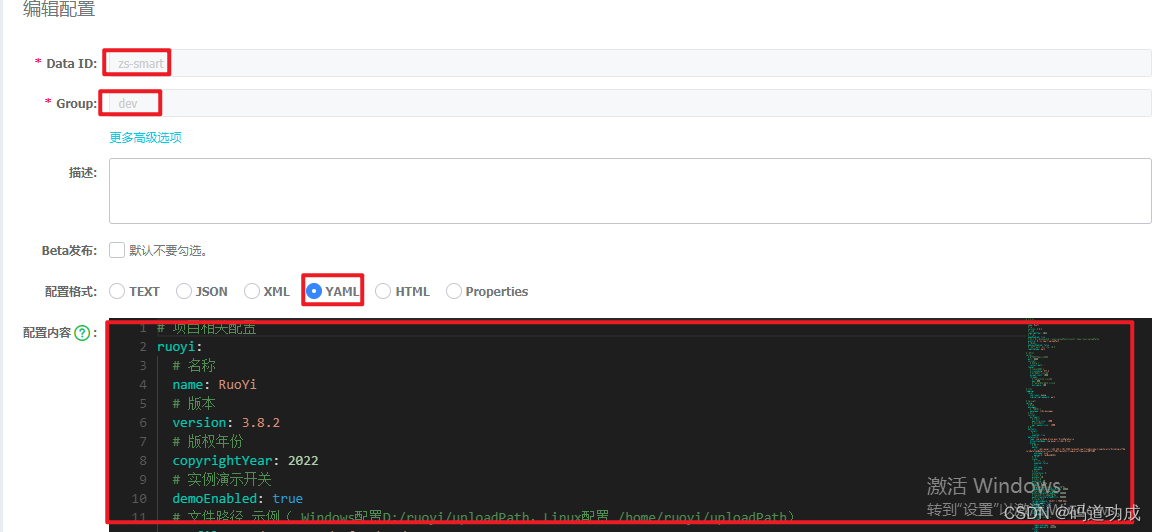
若依前后端分离版集成nacos
根据公司要求,需要将项目集成到nacos中,当前项目是基于若依前后端分离版开发的,若依的版本为3.8.3,若依框架中整合的springBoot版本为2.5.14。Nacos核心提供两个功能:服务注册与发现,动态配置管理。 一、服…...
)
JAVA面试八股文一(mysql)
B-Tree和BTree区别共同点;一个节点可以有多个元素, 排好序的不同点:BTree叶子节点之间有指针,非叶子节点之间的数据都冗余了一份在叶子节点BTree是B-Tree 的升级mysql什么情况设置了索引,但无法使用a.没符合最左原则b.…...

动静态库概念及创建
注意在库中不能写main()函数。 复习gcc指令 预处理-E-> xx.i 编译 -S-> xx.s 汇编 -c-> xx.o 汇编得到的 xx.o称为目标可重定向二进制文件,此时的文件需要把第三方库链接进来才变成可执行程序。 gcc -o mymath main.c myadd.c mysub.c得到的mymath可以执…...
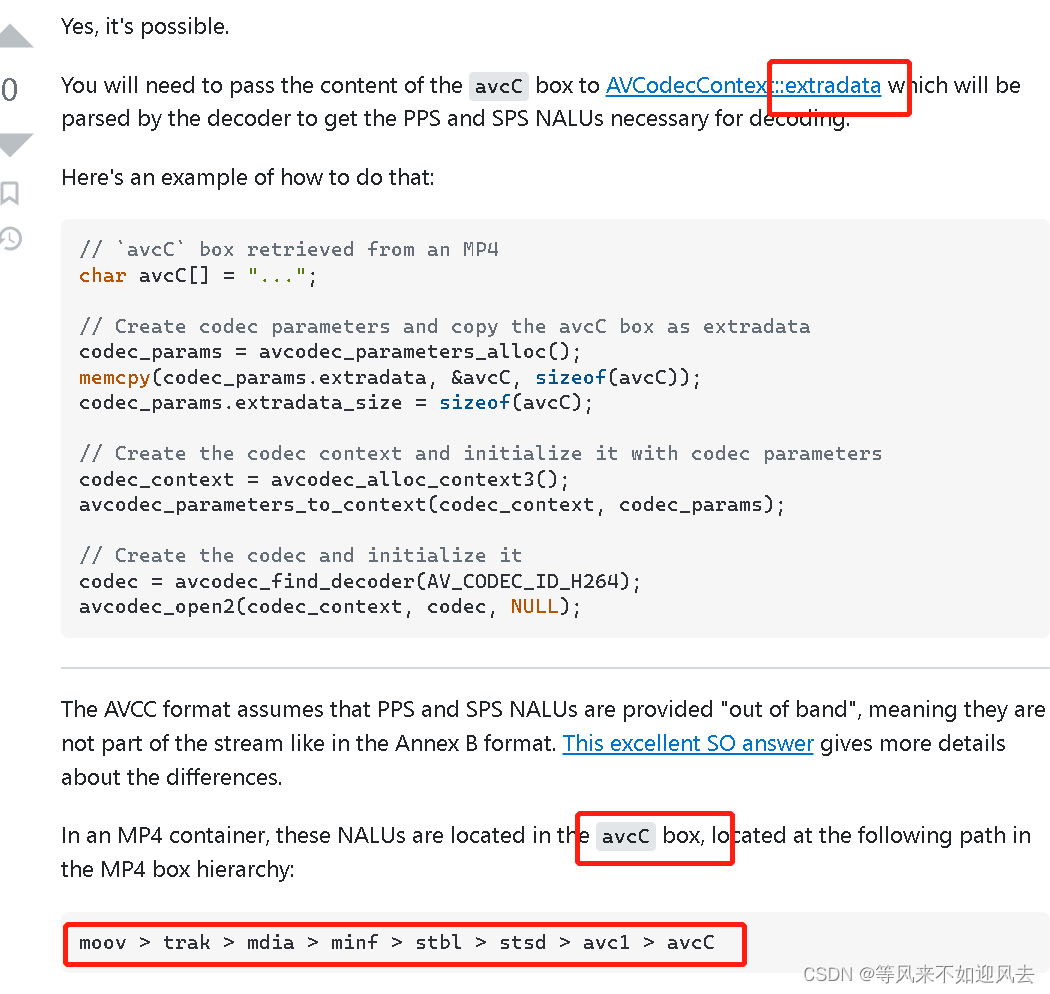
【H.264】码流解析 annexb vs avcc
H264码流解析及NALUAVCC和ANNEXB 前者是FLV容器、mp4 常用的。后者 是实时传输使用,所以是TS 一类的标准。VLC显示AVC1就是AVCC AVCC格式 也叫AVC1格式,MPEG-4格式,字节对齐,因此也叫Byte-Stream Format。用于mp4/flv/mkv, VideoToolbox。 – Annex-B格式 也叫MPEG-2 trans…...

【最优化方法】1-最优化方法介绍
文章目录1 最优化起源2 最优化发展3 运筹学在国外4 运筹学在国内5 什么是最优化?6 为什么要研究最优化问题?7 最优化问题8 最优化问题分类9 最优化研究内容理论算法应用1 最优化起源 中国古代优化思想–田忌赛马(公元前340年) 18世纪L.Euler࿰…...

数据结构 | 树 | 二叉树
🔥Go for it!🔥 📝个人主页:按键难防 📫 如果文章知识点有错误的地方,请指正!和大家一起学习,一起进步👀 📖系列专栏:数据结构与算法 ὒ…...

笔记:使用 unbuild 搭建 JavaScript 构建系统笔记
使用 unbuild 搭建 JavaScript 构建系统jcLee95:https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 邮箱 :291148484163.com 简介: 本文是笔者阅读分析 elementPlus 项目时记录的。该项目用到了一个完全没有文档和资料的工具 unbu…...
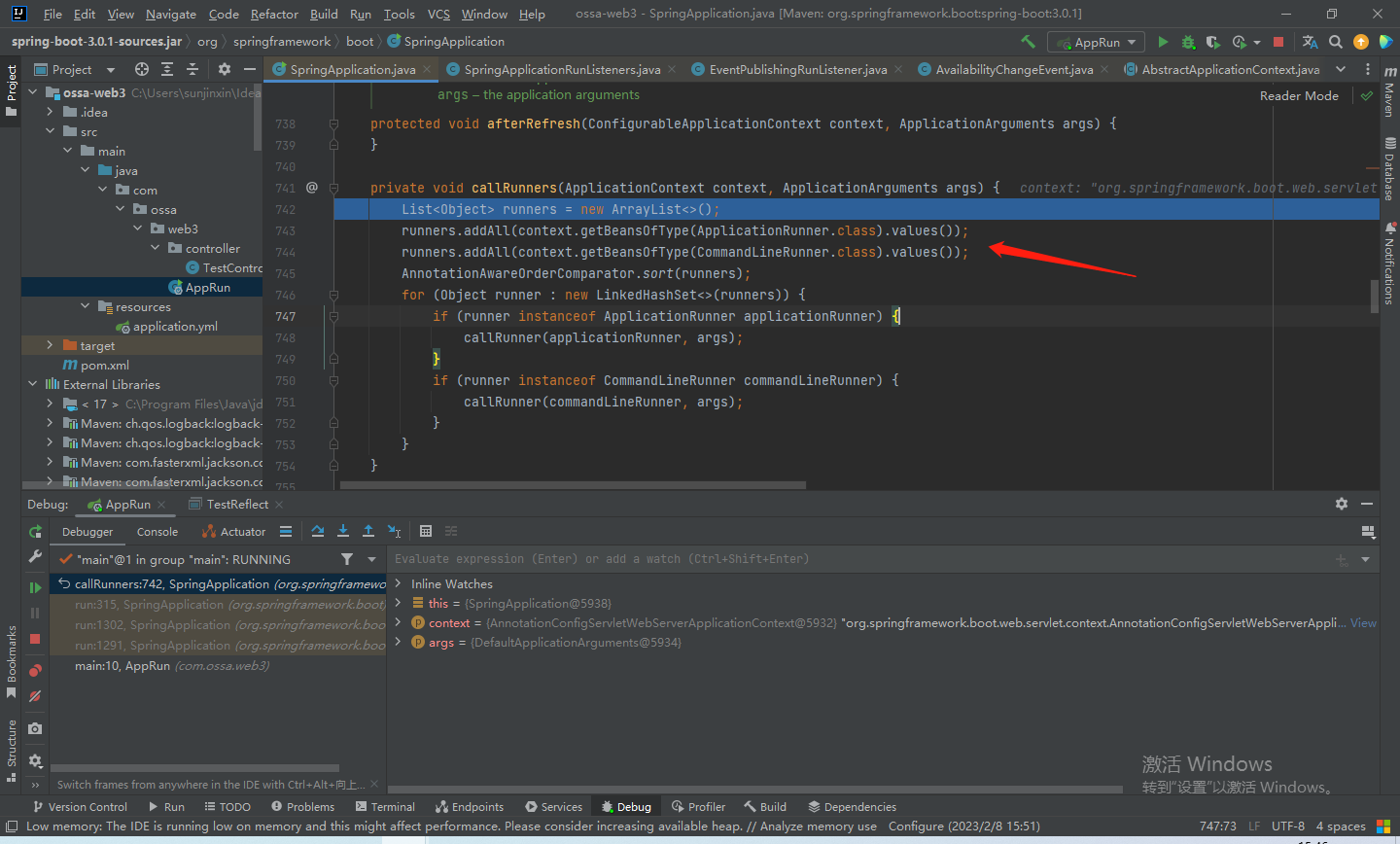
【SpringBoot3.0源码】启动流程源码解析 •下
文章目录初始化DefaultBootstrapContext开启Headless模式获取监听器并启动封装命令行参数准备环境打印Banner创建上下文容器预初始化上下文容器刷新Spring容器打印启动时间发布事件执行特定的run方法上一篇《【SpringBoot3.0源码】启动流程源码解析 • 上》,主要讲解…...
QT(56)-动态链接库-windows-导出变量-导出类
1.导出变量 1.1不使用_declspec(dllimport) _declspec(dllexport) 使用_declspec(dllimport) _declspec(dllexport) 1.2win32 mydllwin32 myexe 1.3win32 mydllqt myexe 2.导出类 使用_declspec(dllimport) _declspec(dllexport) 2.1不用关键…...
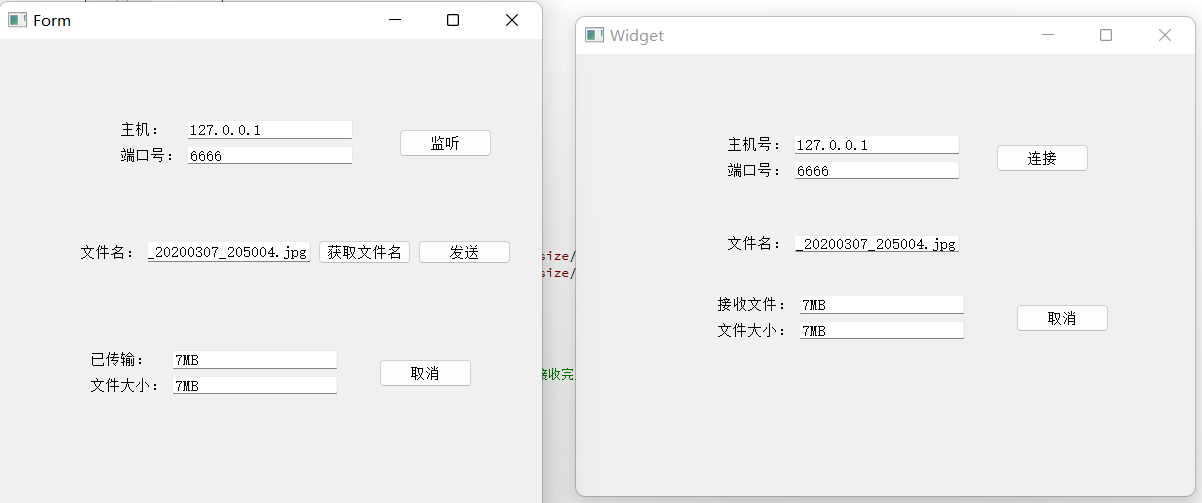
TCP传输文件
传输文件和传输信息的区别: 传输信息,只是一条数据,传输文件是多条数据传输信息传输过去一般都会显示,传输文件一般不会显示,一般只是存放在文件中传输文件需要传输,文件大小和文件名称(不然不知…...
vue3:加载本地图片等静态资源
背景 在我们用 vue2 webpack 的时候,加载图片资源是这样用的: <img :src"require(/assets/test.png)" />这样打包后就会触发 file-loader 打包图片资源,在 dist 文件夹中就可以看到这个图片(如果图片较小会打包…...

工作记录------数据库group_concat函数长度问题
工作记录------group_concat函数长度问题 背景:页面在数据展示时,报错,错误显示:String index out of range: -1 异常信息 java.lang.StringIndexOutOfBoundsException: String index out of range: -1at java.lang.String.sub…...
Python基础语法
1 编程环境 1.1 编译环境 pycharmpython/anaconda 1.2 环境设置 File -> settings -> Project interpreter -> 1.3 Hello world 2 条件判断 2.1 例题 【题1】输入一个年份,判断是否是闰年 ①能被4整除,但不能被100整除; ②能被400整…...
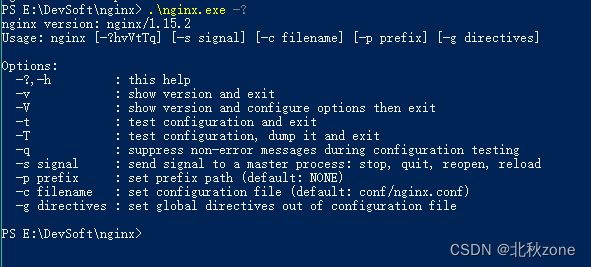
windows环境下安装Nginx及常用操作命令
windows环境下安装Nginx及常用操作命令nginx基本概述基本用途nginx安装nginx基本概述 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器。基本用途 nginx是一个轻量级高并发服务器,而tomcat并不是。nginx一般被用来做反向代理,将请求转发到应用…...

python excel数据处理?
前段时间做了个小项目,帮个海洋系的教授做了个数据处理的软件。基本的功能很简单,就是对Excel里面的一些数据进行过滤,统计,对多个表的内容进行合并等。之前没有处理Excel数据的经验,甚至于自己都很少用到Excel。记得《…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...
