一文教你快速估计个股交易成本
交易本身对市场会产生影响,尤其是短时间内大量交易,会影响金融资产的价格。一个订单到来时的市场价格和订单的执行价格通常会有差异,这个差异通常被称为交易成本。在量化交易的策略回测部分,不考虑交易成本或者交易成本估计不合理,容易导致回测和实盘结果有较大的差异。本文将介绍如何在分布式时序数据库DolphinDB中,如何使用asof join和window join快速估计每个股票的交易成本。
需要的数据包括含有逐笔交易的交易表trades和包含level 1报价的quotes表。它们分别包含以下字段:
trades
Symbol:股票代码
Time:时间
Trade_Volume:交易量
Trade_Price:交易价格
quotes
Symbol:股票代码
Time:时间
Bid_Price:买方报价
Offer_Price:卖方报价
实验中用到的数据都是从纽约证券交易所获取,大家可以从NYSE的ftp下载。参考附录1。
计算股票的交易成本,我们需要找到一个基准价格,通常会把与实际交易最近的一次报价的中间价作为基准价。这意味着要对交易记录表和买卖报价表进行连接。但是,成交和买卖报价的发生时间不可能完全一致,因此不能使用常用的等值连接(equal join)。DolphinDB提供了两种专门为时序数据设计的连接方式:asof join和window join。我们将使用这两种连接方式来计算股票的交易成本。
第一种方法:使用asof join
使用交易发生前(包括交易时刻)的最近一次报价的中间加作为基准。使用交易金额做加权平均。乘上10000是为了把结果转化成basis points。函数aj用于两个表的asof join,前两个参数分别是两个需要join的数据表,第三个参数是join的字段。join的时候首先按股票分组,每个组之内再按照时间行进asof join。右表数据(quotes表)必须保证每个股票组内的记录是按照最后一个连接字段(time)升序排列的。
TC = select sum(Trade_Volume*abs(Trade_Price-(Bid_Price+Offer_Price)/2))/sum(Trade_Volume*Trade_Price)*10000 as cost from aj(trades,quotes,`Symbol`Time) group by symbol第二种方法:使用window join
如果你觉得单次报价的偶然性比较大,我们可以取交易前一段时间的报价的均值或中值作为基准价。下面的例子取交易前10ms的报价均值作为基准。pwj是prevailing window join的缩写,该函数比起aj多了两个参数。新增的第三个参数指定相对的时间窗口。因为时间单位是纳秒,-10000000:0 表示从交易的发生时刻到前10ms的窗口。新增的第4个参数是每个窗口中需要计算的一系列聚合函数。
TC = select sum(Trade_Volume*abs(Trade_Price-(Bid_Price+Offer_Price)/2))/sum(Trade_Volume*Trade_Price)*10000 as cost from pwj(trades,quotes,-10000000:0,<[avg(Offer_Price) as Offer_Price, avg(Bid_Price) as Bid_Price]>,`Symbol`Time) group by symbolasof join和window join是DolphinDB专门为时序数据设计的连接方式,不仅简化了时序数据的操作,大大减少了代码量。以上面的交易成本计算为例,仅仅使用了1行SQL代码就完成了所有个股的交易成本计算。
DolphinDB对两种连接方式实现做了大量的优化,运行速度极快。我们以2016年10月24日纽约证券交易所的股票交易数据和买卖报价数据为例。股票交易表有8023只股票共2700万条交易记录,买卖报价表有7000万条记录。如此庞大的数据量,使用第一种方法,DolphinDB执行耗时仅470多毫秒;使用第二种方法,DolphinDB执行耗时仅825毫秒,速度极快。
最后我们看看结果是不是make sense。观察一下三个股票的交易成本:GS(高盛),TSLA(特斯拉),AAPL(苹果)。
select * from TC where symbol in `GS`TSLA`AAPL第一种方法的结果:
symbol cost
AAPL 0.5446
GS 1.2678
TSLA 16.6456第二种方法的结果:
symbol cost
AAPL 0.535
GS 1.1543
TSLA 18.1025感兴趣的朋友可以到官网下载DolphinDB database 试用版计算股票的交易成本。
附录1.生成样本数据
访问ftp://ftp.nyxdata.com/Historical%2Data%20Samples/Daily%20TAQ%20Sample/并且下载EQY_US_ALL_TRADE_20161024.gz和EQY_US_ALL_NBBO_20161024.gz两个文件,然后把它们解压,保存在/DolphinDB/Data目录下,把两个文件的最后一行删除,因为最后一行是用来标记文件结尾的。
sed -i '$ d' EQY_US_ALL_TRADE_20161024
sed -i '$ d' EQY_US_ALL_NBBO_20161024接着,执行下面的脚本。
DATA_DIR = "./DolphinDB/Data"
PTNDB_DIR = DATA_DIR+"/NYSETAQSeq"
db = database(PTNDB_DIR, SEQ, 16)Trades = loadTextEx(db, `Trades, DATA_DIR + "/EQY_US_ALL_TRADE_20161024”,'|')
Quotes = loadTextEx(db, `Quotes, DATA_DIR + "/EQY_US_ALL_NBBO_20161024",'|')表Trades包含2016年10月24日美国股市的所有交易数据。表Quotes包含同一天的全国最佳买卖报价(NBBO)。
相关文章:

一文教你快速估计个股交易成本
交易本身对市场会产生影响,尤其是短时间内大量交易,会影响金融资产的价格。一个订单到来时的市场价格和订单的执行价格通常会有差异,这个差异通常被称为交易成本。在量化交易的策略回测部分,不考虑交易成本或者交易成本估计不合理…...

Leetcode—移除元素、删除有序数组中的重复项、合并两个有序数组
移除元素 此题简单,用双指针方法即可, 如果右指针指向的元素不等于val,它一定是输出数组的一个元素,我们就将右指针指向的元素复制到左指针位置,然后将左右指针同时右移; 如果右指针指向的元素等于 val&…...
大疆 安全开发 C++1面)
面试(十)大疆 安全开发 C++1面
1. 在C++开发中定义一个变量,若不做初始化直接使用会怎样? 如果该变量是一个普通变量,则如果对其进行访问,会返回一个随机值,int类型不一定为0,bool类型也不一定为false 如果该变量为一个静态变量,则初始值都是一个0; 如果该变量是一个指针,那么在后续程序运行中很…...
短信链接跳转微信小程序
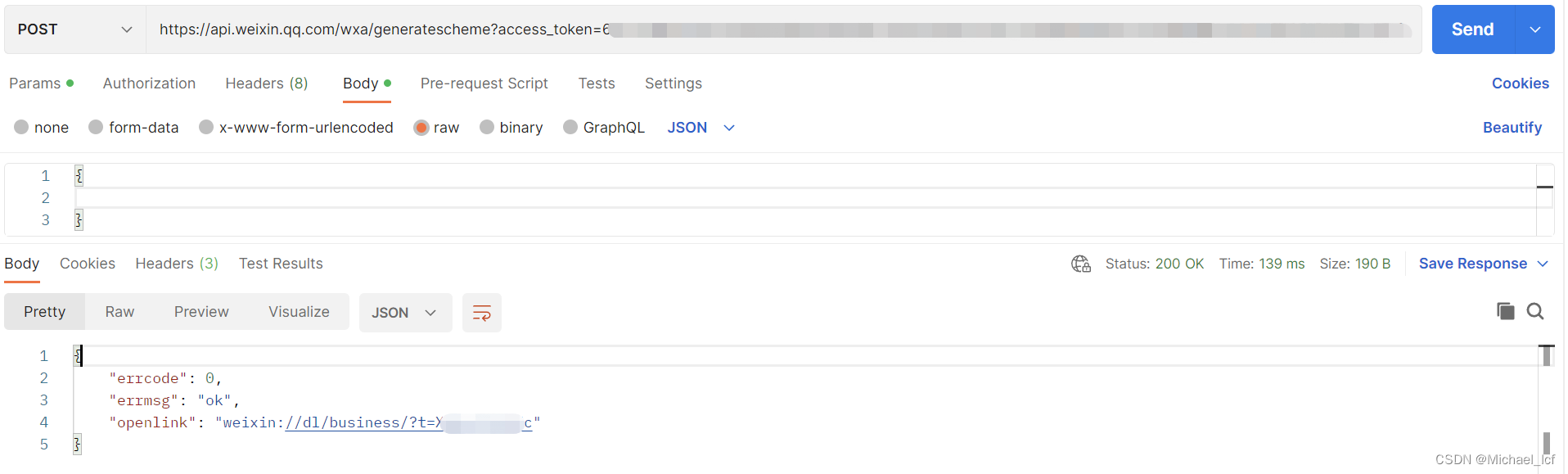
短信链接跳转微信小程序1 实现方案1.1 通过URL Scheme实现1.2 通过URL Link实现1.3 通过云开发静态网站实现2 实现方案对比3 实践 URL Schema 方案3.1 获取微信access_token3.2 获取openlink3.3 H5页面(模拟短信跳转,验证ok)4 问题小节4.1 io…...

吉林电视台启用乾元通多卡聚合系统广电视频传输解决方案
随着广播电视数字化、IP化、智能化的逐步深入,吉林电视台对技术改造、数字设备升级提出了更高要求,通过对系统性能、设计理念的综合评估,正式启用乾元通多卡聚合系统广电视频传输解决方案,将用于大型集会、大型演出、基层直播活动…...
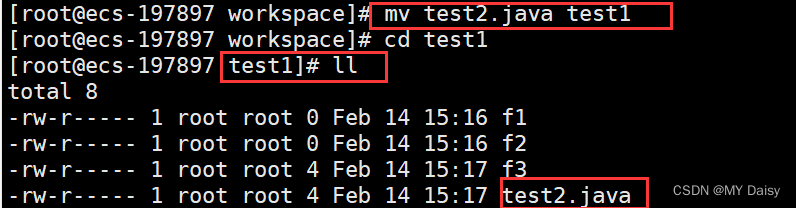
Linux常用命令1
目录1、远程登陆服务器2、文件相关(1)文件和目录属性(2)创建目录mkdir(3)删除目录rmdir(4)创建文件touch(5)删除文件或目录rm(6)ls命令…...

【C++进阶】一、继承(总)
目录 一、继承的概念及定义 1.1 继承概念 1.2 继承定义 1.3 继承基类成员访问方式的变化 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 五、继承与友元 六、继承与静态成员 七、菱形继承及菱形虚拟继承 7.1 继承的分类 7.2 菱形虚拟…...
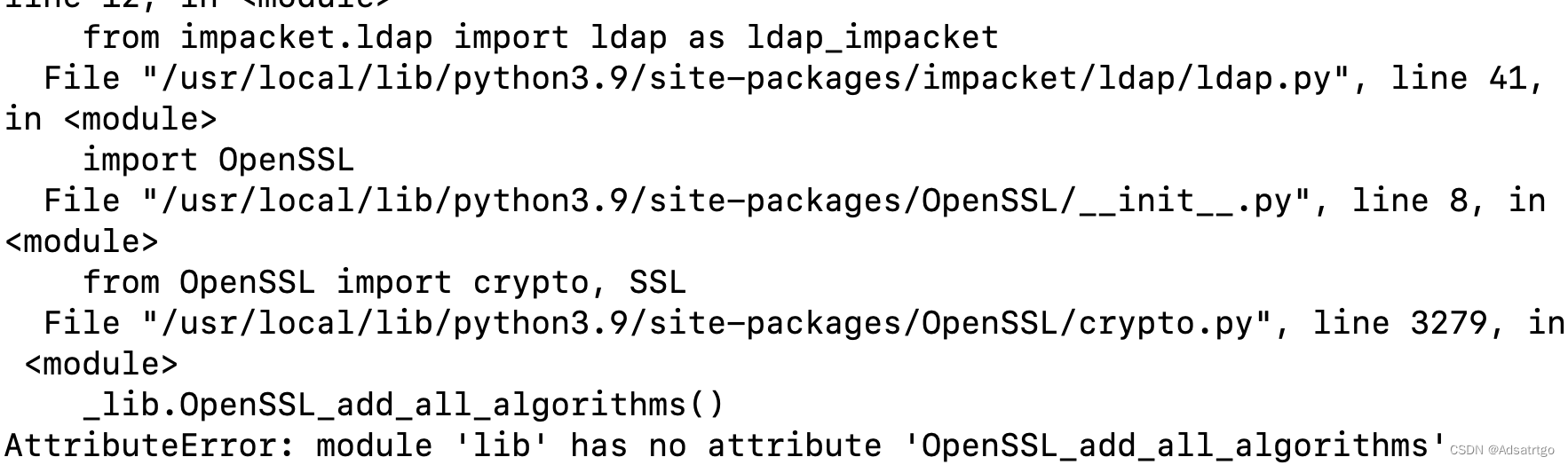
AttributeError: module ‘lib‘ has no attribute ‘OpenSSL_add_all_algorithms
pip安装crackmapexec后,运行crackmapexec 遇到报错 AttributeError: module lib has no attribute OpenSSL_add_all_algorithms 直接安装 pip3 install crackmapexec 解决 通过 python3 -m pip install --upgrade openssl 或者 python3 -m pip install openssl>22.1.…...

Python实现视频自动打码功能,避免看到羞羞的画面
前言 嗨呀嗨呀,最近重温了一档综艺节目 至于叫什么 这里就不细说了 老是看着看着就会看到一堆马赛克,由于太好奇了就找了一下原因,结果是因为某艺人塌房了…虽然但是 看综艺的时候满影响美观的 咳咳,这里我可不是来教你们如何解…...
说说Knife4j
Knife4j是一款基于Swagger2的在线API文档框架使用Knife4j, 需要 添加Knife4j的依赖当前建议使用的Knife4j版本, 只适用于Spring Boot2.6以下版本, 不含Spring Boot2.6 在主配置文件(application.yml)中开启Knife4j的增强模式必须在主配置文件中进行配置, 不要配置在个性化配置文…...
Java学习笔记-03(API阶段-2)集合
集合 我们接下来要学习的内容是Java基础中一个很重要的部分:集合 1. Collection接口 1.1 前言 Java语言的java.util包中提供了一些集合类,这些集合类又称之为容器 提到容器不难想到数组,集合类与数组最主要的不同之处是,数组的长度是固定的,集合的长度是可变的&a…...
)
「3」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 矩阵的秩 定义4:在mxn矩阵A中,任取k行与k列(k<m,k<n),位…...
)
【CSDN竞赛】27期题解(Javascript)
前言 本来排名是20的,不过第一题有点输出bug,最后实际测出来又重新排名,刚好卡在第10。但是考试报告好像过了12小时就下载不到了,所以就只写题目求解的JS函数吧。 1. 幸运数字 小艺定义一个幸运数字的标准包含3条: 仅包含4或7幸…...

高压放大器在骨的逆力电研究中的应用
实验名称:高压放大器在骨的逆力电研究中的应用研究方向:生物医学测试目的:骨中的胶原和羟基磷灰石沿厚度分布不均匀,骨试样在直流电压作用下,内部出现传导电流引起试样内部温度升高,不同组分热变形不一致&a…...
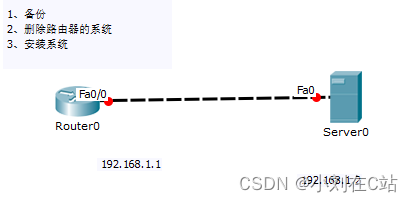
思科网络部署,(0基础)入门实验,超详细
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...
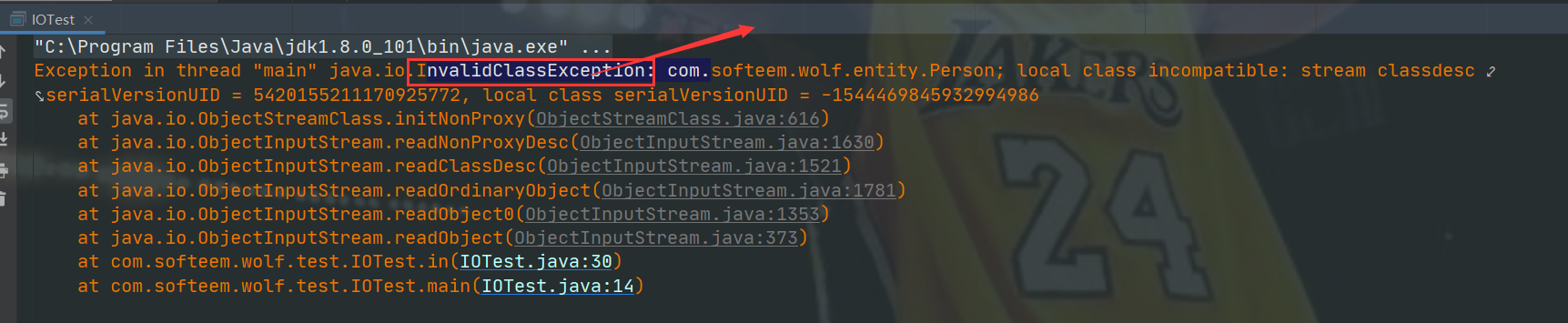
private static final Long serialVersionUID= 1L详解
我们知道在对数据进行传输时,需要将其进行序列化,在Java中实现序列化的方式也很简单,可以直接通过实现Serializable接口。但是我们经常也会看到下面接这一行代码,private static final Long serialVersionUID 1L;这段代…...
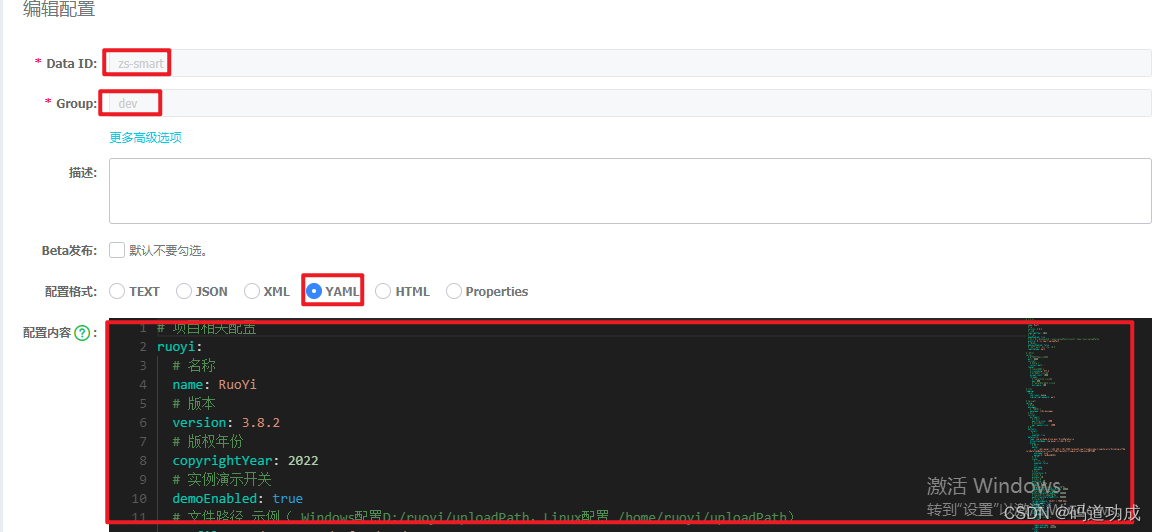
若依前后端分离版集成nacos
根据公司要求,需要将项目集成到nacos中,当前项目是基于若依前后端分离版开发的,若依的版本为3.8.3,若依框架中整合的springBoot版本为2.5.14。Nacos核心提供两个功能:服务注册与发现,动态配置管理。 一、服…...
)
JAVA面试八股文一(mysql)
B-Tree和BTree区别共同点;一个节点可以有多个元素, 排好序的不同点:BTree叶子节点之间有指针,非叶子节点之间的数据都冗余了一份在叶子节点BTree是B-Tree 的升级mysql什么情况设置了索引,但无法使用a.没符合最左原则b.…...

动静态库概念及创建
注意在库中不能写main()函数。 复习gcc指令 预处理-E-> xx.i 编译 -S-> xx.s 汇编 -c-> xx.o 汇编得到的 xx.o称为目标可重定向二进制文件,此时的文件需要把第三方库链接进来才变成可执行程序。 gcc -o mymath main.c myadd.c mysub.c得到的mymath可以执…...
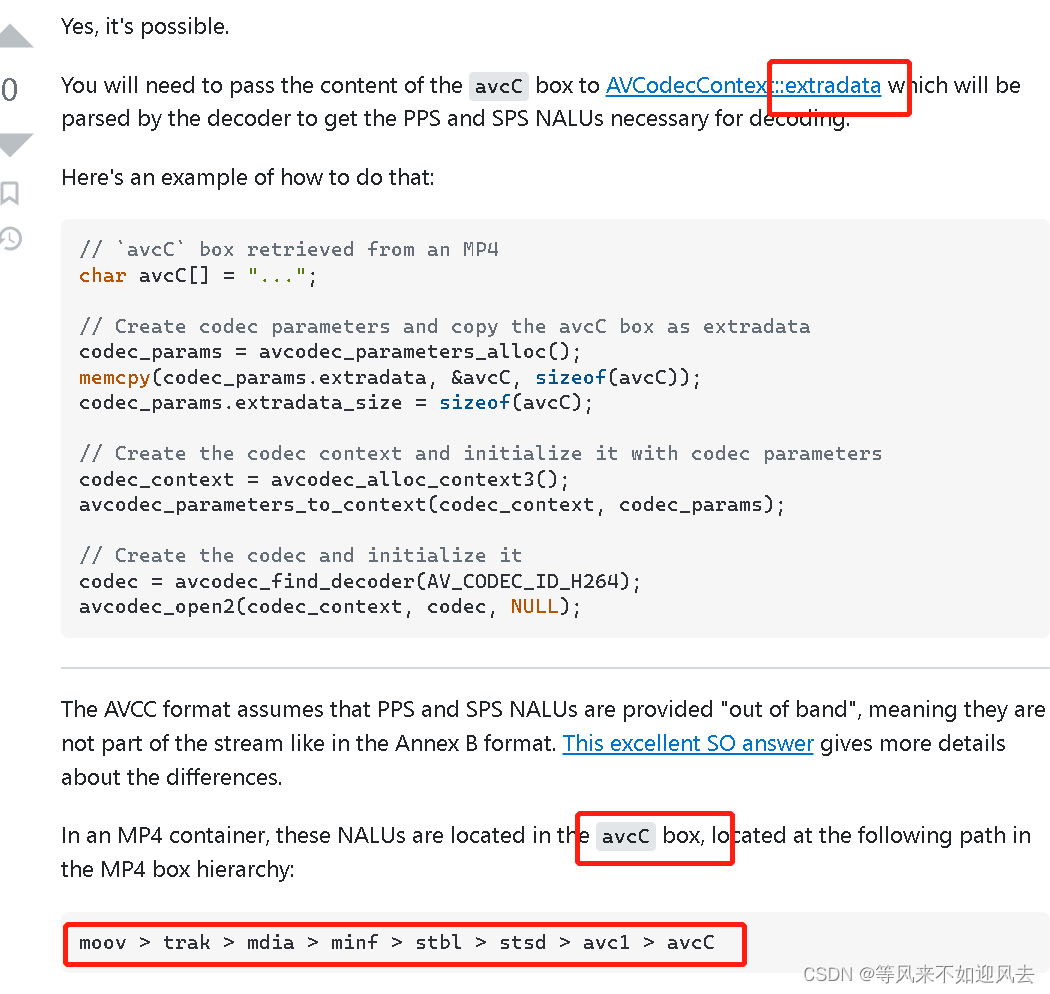
【H.264】码流解析 annexb vs avcc
H264码流解析及NALUAVCC和ANNEXB 前者是FLV容器、mp4 常用的。后者 是实时传输使用,所以是TS 一类的标准。VLC显示AVC1就是AVCC AVCC格式 也叫AVC1格式,MPEG-4格式,字节对齐,因此也叫Byte-Stream Format。用于mp4/flv/mkv, VideoToolbox。 – Annex-B格式 也叫MPEG-2 trans…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
