【学习笔记】CF607E Cross Sum
最后一道数据结构,不能再多了。
而且需要一点计算几何的知识,有点难搞。
分为两个部分求解。
首先考虑找到距离 ≤ r \le r ≤r的交点数量。发现这等价于圆上两段圆弧相交,因此将圆上的点离散化后排序,用一个主席树来求就做完了。
然后是距离求和。这看起来非常棘手。事实上,只要把所有交点都找出来就做完了。首先可以放心的将圆环从一个位置断开。其次,考虑以某种顺序将所有直线依次删掉。发现当按照长度从大到小删时,假设这条线段是 [ l i , r i ] [l_i,r_i] [li,ri],发现只要满足 l j ∈ [ l i , r i ] l_j\in [l_i,r_i] lj∈[li,ri]或者 r j ∈ [ l i , r i ] r_j\in [l_i,r_i] rj∈[li,ri],那么直线 i , j i,j i,j就一定相交。那么前面一个问题也得到了解决,只需用树状树组维护就做完了。
当然,事实上我们可以 O ( 1 ) O(1) O(1)求出一个交点。考虑倒着做,每次删除一条线段,用链表维护就做完了。事实上交点在圆上的情况并不影响答案,所以可以少一些细节。
那么问题来了,为啥我被卡常了。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f
#define db double
#define cpx complex<db>
using namespace std;
const int N=1e5+5;
struct seg{db k,b;
}seg[N];
struct point{db x,y;
}p;
int n,m,cntseg,cnt;
int bit[N],sa[N],pos[N];
int le[N],ri[N],L[N],R[N];//链表
db res;
pair<db,int>A[N];
bool cmp(int x,int y){return R[x]-L[x]<R[y]-L[y];
}
ll ask(int x){ll tot=0;for(;x;x-=x&-x)tot+=bit[x];return tot;
}
void add(int x,int y){for(;x<=cnt;x+=x&-x)bit[x]+=y;
}
db getdist(point x,point y){return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));
}
point calc(int x,int y){x=pos[x],y=pos[y];db tx=(seg[y].b-seg[x].b)/(seg[x].k-seg[y].k),ty=seg[x].k*tx+seg[x].b;return {tx,ty};
}
void del(int x){if(le[x])ri[le[x]]=ri[x];if(ri[x])le[ri[x]]=le[x];
}
ll check(db mid){ll res=0;cntseg=cnt=0;for(int i=1;i<=n;i++){db dist=abs(seg[i].k*p.x-p.y+seg[i].b)/sqrt(seg[i].k*seg[i].k+1);if(dist<=mid){db a=seg[i].k*seg[i].k+1,b=2*seg[i].k*(seg[i].b-p.y)-2*p.x,c=p.x*p.x+(seg[i].b-p.y)*(seg[i].b-p.y)-mid*mid;db delta=b*b-4*a*c;db lx=(-b-sqrt(delta))/(2*a),ly=seg[i].k*lx+seg[i].b;db rx=(-b+sqrt(delta))/(2*a),ry=seg[i].k*rx+seg[i].b;cntseg++;L[cntseg]=R[cntseg]=0;//fixedpos[cntseg]=i;A[++cnt]={atan2(ry-p.y,rx-p.x),cntseg};A[++cnt]={atan2(ly-p.y,lx-p.x),cntseg};}}sort(A+1,A+1+cnt);for(int i=1;i<=cnt;i++){if(!L[A[i].se])L[A[i].se]=i;else R[A[i].se]=i;}for(int i=1;i<=cntseg;i++){sa[i]=i;}sort(sa+1,sa+1+cntseg,cmp);for(int i=1;i<=cnt;i++)le[i]=i-1,ri[i]=i+1;ri[cnt]=0;for(int i=1;i<=cnt;i++)add(i,1);for(int i=1;i<=cntseg;i++){int x=sa[i];res+=ask(R[x]-1)-ask(L[x]);add(L[x],-1),add(R[x],-1);del(L[x]),del(R[x]);}return res;
}
db getans(db mid){ll res=0;db tot=0;cntseg=cnt=0;for(int i=1;i<=n;i++){db dist=abs(seg[i].k*p.x-p.y+seg[i].b)/sqrt(seg[i].k*seg[i].k+1);if(dist<=mid){db a=seg[i].k*seg[i].k+1,b=2*seg[i].k*(seg[i].b-p.y)-2*p.x,c=p.x*p.x+(seg[i].b-p.y)*(seg[i].b-p.y)-mid*mid;db delta=b*b-4*a*c;db lx=(-b-sqrt(delta))/(2*a),ly=seg[i].k*lx+seg[i].b;db rx=(-b+sqrt(delta))/(2*a),ry=seg[i].k*rx+seg[i].b;cntseg++;L[cntseg]=R[cntseg]=0;//fixedpos[cntseg]=i;A[++cnt]={atan2(ry-p.y,rx-p.x),cntseg};A[++cnt]={atan2(ly-p.y,lx-p.x),cntseg};}}sort(A+1,A+1+cnt);for(int i=1;i<=cnt;i++){if(!L[A[i].se])L[A[i].se]=i;else R[A[i].se]=i;}for(int i=1;i<=cntseg;i++)sa[i]=i;sort(sa+1,sa+1+cntseg,cmp);for(int i=1;i<=cnt;i++)le[i]=i-1,ri[i]=i+1;ri[cnt]=0;for(int i=1;i<=cnt;i++)add(i,1);for(int i=1;i<=cntseg;i++){int x=sa[i];for(int j=ri[L[x]];j!=R[x];j=ri[j]){point tmp=calc(x,A[j].se);res++;tot+=getdist(p,tmp);}add(L[x],-1),add(R[x],-1);del(L[x]),del(R[x]);}return tot+(m-res)*mid;
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>p.x>>p.y>>m;p.x/=1000,p.y/=1000;//fixedfor(int i=1;i<=n;i++){cin>>seg[i].k>>seg[i].b;seg[i].k/=1000,seg[i].b/=1000;}db l=0,r=4e9;for(int i=1;i<=100;i++){db mid=(l+r)/2;if(check(mid)<=m)l=mid;else r=mid;}//fixedcout.precision(20);cout<<getans(l);
}
相关文章:

【学习笔记】CF607E Cross Sum
最后一道数据结构,不能再多了。 而且需要一点计算几何的知识,有点难搞。 分为两个部分求解。 首先考虑找到距离 ≤ r \le r ≤r的交点数量。发现这等价于圆上两段圆弧相交,因此将圆上的点离散化后排序,用一个主席树来求就做完了…...

Python 一元线性回归模型预测实验完整版
一元线性回归预测模型 实验目的 通过一元线性回归预测模型,掌握预测模型的建立和应用方法,了解线性回归模型的基本原理 实验内容 一元线性回归预测模型 实验步骤和过程 (1)第一步:学习一元线性回归预测模型相关知识。 线性回归模型属于…...

GStreamer第一阶段的简单总结
这里写目录标题 前言个人的总结v4l2src插件的简单使用 前言 因为涉及很多细节的GStreamer官方论坛有详细解链接: GStreamer官网,这里不做说明,以下只是涉及到个人的理解和认知,方便后续的查阅。 个人的总结 1)了解pipeline的使用࿰…...

【网络进阶】服务器模型Reactor与Proactor
文章目录 1. Reactor模型2. Proactor模型3. 同步IO模拟Proactor模型 在高并发编程和网络连接的消息处理中,通常可分为两个阶段:等待消息就绪和消息处理。当使用默认的阻塞套接字时(例如每个线程专门处理一个连接),这两…...

使用div替代<frameset><frame>的问题以及解决办法
首先是原版三层框架的html: <html> <head> <title>THPWP</title> </head> <!-- 切记frameset不能写在body里面,以下代表首页由三层模块组成,其中第一层我是用来放菜单高度占比14%,中间的用作主…...

Verilog中的`define与`if的使用
一部分代码可能有时候用,有时候不用,为了避免全部编译占用资源,可以使用条件编译语句。 语法 // Style #1: Only single ifdef ifdef <FLAG>// Statements endif// Style #2: ifdef with else part ifdef <FLAG>// Statements …...

沃尔玛、亚马逊影响listing的转化率4大因素,测评补单自养号解析
1、listing的相关性:前期我们在找词,收集词的时候,我们通过插件来协助我们去筛选词。我们把流量高,中,低的关键词都一一收集,然后我们再进行对收集得来的关键词进行分析,再进行挑词,…...

静态分析和动态分析
在开发早期,发现并修复bug在许多方面都有好处。它可以减少开发时间,降低成本,并且防止数据泄露或其他安全漏洞。特别是对于DevOps,尽早持续地将测试纳入SDLC软件开发生命周期是非常有帮助的。 这就是动态和静态分析测试的用武之地…...

代码随想录_贪心_leetcode 1005 134
leetcode 1005. K 次取反后最大化的数组和 1005. K 次取反后最大化的数组和 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以…...

笔记:对多维torch进行任意维度的多“行”操作
如何取出多维torch指定维度的指定“行” 从二维torch开始新建torch取出某一行取出某一列一次性取出多行取出连续的多行取出不连续的多行 一次取出多列取出连续的多列取出不连续的多列 考虑三维torch取出三维torch的任意两行(means 在dim0上操作)取出连续…...
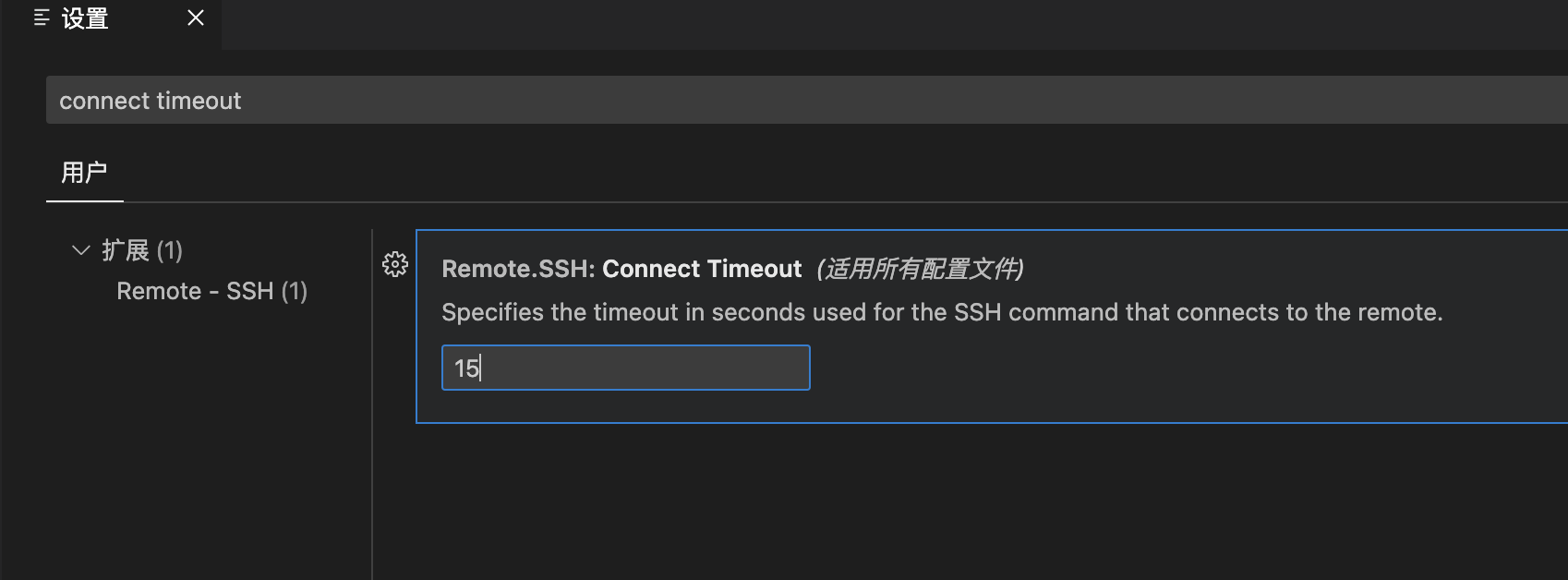
【VSCode】1、VSCode 如何连接服务器
文章目录 一、安装 remote-ssh 插件二、直接连接三、配置 SSH 公匙,免密登录 一、安装 remote-ssh 插件 点击插件搜索框,搜 remote-ssh,点击安装 安装完成后就会出现下面的图标: 二、直接连接 点击加号,输入 ssh 连接…...

AI工具:通过智能实现工作和学习效率的革命化
AI工具是指一系列人工智能技术和工具,包括机器学习、深度学习、自然语言处理、计算机视觉等。这些工具可以帮助开发人员和数据科学家通过处理和分析海量数据来自动识别和解决问题,提供智能的决策和预测模型。常见的AI工具包括TensorFlow、PyTorch、Keras…...

static 和构造方法
文章目录 static构造方法内存中数据的存储方式示例 static 具体对象的属性,称之为对象属性,成员属性,实例属性。 具体对象的方法,称之为对象方法,成员方法,实例方法。 静态:static 和具体对…...

【Linux 裸机篇(八)】I.MX6U EPIT 定时器中断、定时器按键消抖
目录 一、EPIT 定时器简介二、定时器按键消抖 一、EPIT 定时器简介 EPIT 的全称是: Enhanced Periodic Interrupt Timer,直译过来就是增强的周期中断定时器,它主要是完成周期性中断定时的。学过 STM32 的话应该知道, STM32 里面的…...

Web安全 XSS靶场搭建(玩转整个XSS环境.)
Web安全 XSS靶场搭建 XSS又叫CSS(Cross Site Script)跨站脚本攻击,指的是攻击者在Web页面,插入恶意JS代码,当用户浏览该页之时,嵌入其中JS代码就会被执行,从而达到攻击的目的.(包含…...
)
前端开发技术——DOM(上)
一.单选题(共4题,44.4分) 1 下列选项中,关于事件的描述错误的是() A、 事件指的是可以被JavaScript侦测到的行为 B、 事件驱动程序指的是事件触发后要执行的代码 C、 事件源是指触发的事件 D、 事件的种类称为事件…...

银河麒麟v10服务器版安装OpenDDS
1. OpenDDS简介 OpenDDS是OMG数据分发服务(DDS)的一种开源实现,它遵循实时系统v1.2的DDS规范(OMG Document formal/07-01-01)和实时公布/订阅互操作性通信协议v2.1的DDS-RTPS规范(OMG Document formal/2010-11-01)。OpenDDS由OCI公司设计和维护,可从http…...

curl方式调用电商API接口示例 详细介绍
cURL是一个利用URL语法在命令行下工作的文件传输工具,1997年首次发行。它支持文件上传和下载,所以是综合传输工具,但按传统,习惯称cURL为下载工具。cURL还包含了用于程序开发的libcurl。 cURL支持的通信协议有FTP、FTPS、HTTP、H…...

Duboo介绍与入门
文章目录 1、Dubbo的前世今生2、Dubbo的快速入门2.1、Dubbo的基本架构2.2、Nacos2.3、管理后台2.4、入门案例2.4.1、服务提供者搭建环境代码实现配置文件 2.4.2、服务消费者搭建环境代码实现配置文件 最后说一句 1、Dubbo的前世今生 2011年10月27日,阿里巴巴开源了…...
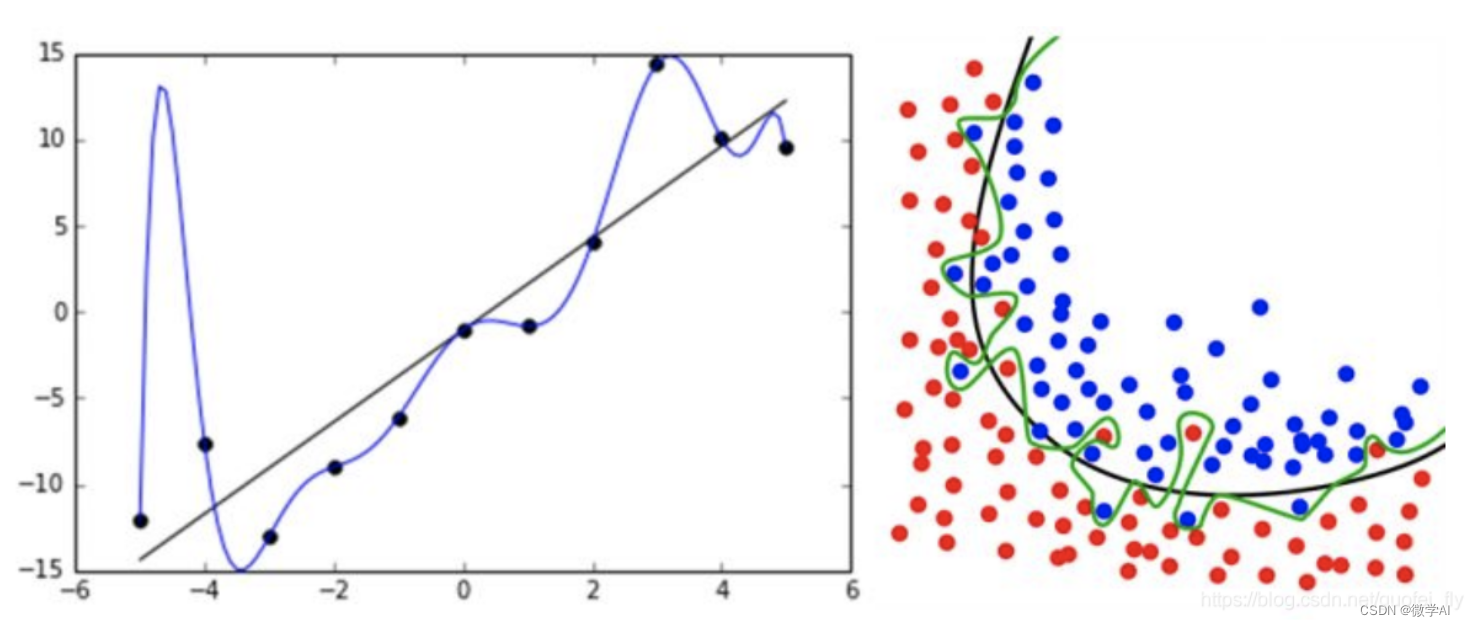
人工智能中(Pytorch)框架下模型训练效果的提升方法
大家好,我是微学AI,今天给大家介绍一下人工智能中(Pytorch)框架下模型训练效果的提升方法。随着深度学习技术的快速发展,越来越多的应用场景需要建立复杂的、高精度的深度学习模型。为了实现这些目标,必须采用一系列复杂的技术来提…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
