# 数据结构和算法面试题系列-随机算法总结
0 概述
随机算法涉及大量概率论知识,有时候难得去仔细看推导过程,当然能够完全了解推导的过程自然是有好处的,如果不了解推导过程,至少记住结论也是必要的。本文总结最常见的一些随机算法的题目,是几年前找工作的时候写的。需要说明的是,这里用到的随机函数 randInt(a, b) 假定它能随机的产生范围 [a,b] 内的整数,即产生每个整数的概率相等(虽然在实际中并不一定能实现,不过不要太在意,这个世界很多事情都很随机)。
1 随机排列数组
假设给定一个数组 A,它包含元素 1 到 N,我们的目标是构造这个数组的一个均匀随机排列。
一个常用的方法是为数组每个元素 A[i] 赋一个随机的优先级 P[i],然后依据优先级对数组进行排序。比如我们的数组为 A = {1, 2, 3, 4},如果选择的优先级数组为 P = {36, 3, 97, 19},那么就可以得到数列 B={2, 4, 1, 3},因为 3 的优先级最高(为97),而 2 的优先级最低(为3)。这个算法需要产生优先级数组,还需使用优先级数组对原数组排序,这里就不详细描述了,还有一种更好的方法可以得到随机排列数组。
产生随机排列数组的一个更好的方法是原地排列(in-place)给定数组,可以在 O(N) 的时间内完成。伪代码如下:
RANDOMIZE-IN-PLACE ( A , n ) for i ←1 to n do swap A[i] ↔ A[RANDOM(i , n )]
如代码中所示,第 i 次迭代时,元素 A[i] 是从元素 A[i...n]中随机选取的,在第 i 次迭代后,我们就再也不会改变 A[i]。
A[i] 位于任意位置j的概率为 1/n。这个是很容易推导的,比如 A[1] 位于位置 1 的概率为 1/n,这个显然,因为 A[1] 不被1到n的元素替换的概率为 1/n,而后就不会再改变 A[1] 了。而A[1] 位于位置 2 的概率也是 1/n,因为 A[1] 要想位于位置2,则必须在第一次与 A[k] (k=2…n) 交换,同时第二次 A[2] 与 A[k]替换,第一次与 A[k] 交换的概率为(n-1)/n,而第二次替换概率为 1/(n-1),所以总的概率是 (n-1)/n * 1/(n-1) = 1/n。同理可以推导其他情况。
当然这个条件只能是随机排列数组的一个必要条件,也就是说,满足元素 A[i] 位于位置 j 的概率为1/n 不一定就能说明这可以产生随机排列数组。因为它可能产生的排列数目少于 n!,尽管概率相等,但是排列数目没有达到要求,算法导论上面有一个这样的反例。
算法 RANDOMIZE-IN-PLACE可以产生均匀随机排列,它的证明过程如下:
首先给出k排列的概念,所谓 k 排列就是从n个元素中选取k个元素的排列,那么它一共有 n!/(n-k)! 个 k 排列。
循环不变式:for循环第i次迭代前,对于每个可能的i-1排列,子数组A[1…i-1]包含该i-1排列的概率为 (n-i+1)! / n!。
-
初始化:在第一次迭代前,i=1,则循环不变式指的是对于每个0排列,子数组A[1…i-1]包含该0排列的概率为
(n-1+1)! / n! = 1。A[1…0]为空的数组,0排列则没有任何元素,因此A包含所有可能的0排列的概率为1。不变式成立。 -
维持:假设在第i次迭代前,数组的i-1排列出现在
A[1...i-1]的概率为(n-i+1) !/ n!,那么在第i次迭代后,数组的所有i排列出现在A[1...i]的概率为(n-i)! / n!。下面来推导这个结论:- 考虑一个特殊的 i 排列 p = {x1, x2, … xi},它由一个 i-1 排列 p’ ={x1, x2,…, xi−1} 后面跟一个 xi 构成。设定两个事件变量E1和E2:
-
E1为该算法将排列
p'放置到A[1...i-1]的事件,概率由归纳假设得知为Pr(E1) = (n-i+1)! / n!。 -
E2为在第 i 次迭代时将 xi 放入到
A[i]的事件。
因此我们得到 i 排列出现在A[1...i]的概率为Pr {E2 ∩ E1} = Pr {E2 | E1} Pr {E1}。而Pr {E2 | E1} = 1/(n − i + 1),所以
Pr {E2 ∩ E1} = Pr {E2 | E1} Pr {E1}= 1 /(n − i + 1) * (n − i + 1)! / n! = (n − i )! / n!。 -
结束:结束的时候
i=n+1,因此可以得到A[1...n]是一个给定 n 排列的概率为1/n!。
C实现代码如下:
void randomInPlace(int a[], int n)
{int i;for (i = 0; i < n; i++) {int rand = randInt(i, n-1);swapInt(a, i, rand);}
}
扩展
如果上面的随机排列算法写成下面这样,是否也能产生均匀随机排列?
PERMUTE-WITH-ALL( A , n ) for i ←1 to n do swap A[i] ↔A[RANDOM(1 , n )]
注意,该算法不能产生均匀随机排列。假定 n=3,则该算法可以产生3*3*3=27个输出,而3个元素只有3!=6个不同的排列,要使得这些排列出现概率等于 1/6,则必须使得每个排列出现次数 m 满足m/27=1/6,显然,没有这样的整数符合条件。而实际上各个排列出现的概率如下,如 {1,2,3} 出现的概率为4/27,不等于 1/6。
| 排 列 | 概 率 |
|---|---|
| <1, 2, 3> | 4/27 |
| <1, 3, 2> | 5/27 |
| <2, 1, 3> | 5/27 |
| <2, 3, 1> | 5/27 |
| ❤️, 1, 2> | 4/27 |
| ❤️, 2, 1> | 4/27 |
2 随机选取一个数字
题: 给定一个未知长度的整数流,如何随机选取一个数?(所谓随机就是保证每个数被选取的概率相等)
解1: 如果数据流不是很长,可以存在数组中,然后再从数组中随机选取。当然题目说的是未知长度,所以如果长度很大不足以保存在内存中的话,这种解法有其局限性。
解2: 如果数据流很长的话,可以这样:
- 如果数据流在第1个数字后结束,那么必选第1个数字。
- 如果数据流在第2个数字后结束,那么我们选第2个数字的概率为1/2,我们以1/2的概率用第2个数字替换前面选的随机数,得到新的随机数。
- …
- 如果数据流在第n个数字后结束,那么我们选择第n个数字的概率为1/n,即我们以1/n的概率用第n个数字替换前面选的随机数,得到新的随机数。
一个简单的方法就是使用随机函数 f(n)=bigrand()%n,其中 bigrand() 返回很大的随机整数,当数据流到第 n 个数时,如果 f(n)==0,则替换前面的已经选的随机数,这样可以保证每个数字被选中的概率都是 1/n。如当 n=1 时,则f(1)=0,则选择第 1 个数,当 n=2 时,则第 2 个数被选中的概率都为 1/2,以此类推,当数字长度为 n 时,第 n 个数字被选中的概率为 1/n。代码如下(注:在 Linux/MacOS 下,rand() 函数已经可以返回一个很大的随机数了,就当做bigrand()用了):
void randomOne(int n)
{int i, select = 0;for (i = 1; i < n; i++) {int rd = rand() % n;if (rd == 0) {select = i;}}printf("%d\n", select);
}
3 随机选取M个数字
题: 程序输入包含两个整数 m 和 n ,其中 m<n,输出是 0~n-1 范围内的 m 个随机整数的有序列表,不允许重复。从概率角度来说,我们希望得到没有重复的有序选择,其中每个选择出现的概率相等。
解1: 先考虑个简单的例子,当 m=2,n=5 时,我们需要从 0~4 这 5 个整数中等概率的选取 2 个有序的整数,且不能重复。如果采用如下条件选取:bigrand() % 5 < 2,则我们选取 0 的概率为2/5。但是我们不能采取同样的概率来选取 1,因为选取了 0 后,我们应该以 1/4 的概率来选取1,而在没有选取0的情况下,我们应该以 2/4 的概率选取1。选取的伪代码如下:
select = m
remaining = n
for i = [0, n)if (bigrand() % remaining < select)print iselect--remaining--
只要满足条件 m<=n,则程序输出 m 个有序整数,不多不少。不会多选,因为每选择一个数,select--,这样当 select 减到 0 后就不会再选了。同时,也不会少选,因为每次都会remaining--,当 select/remaining=1 时,一定会选取一个数。每个子集被选择的概率是相等的,比如这里5选2则共有 C(5,2)=10 个子集,如 {0,1},{0,2}...等,每个子集被选中的概率都是 1/10。
更一般的推导,n选m的子集数目一共有 C(n,m) 个,考虑一个特定的 m 序列,如0...m-1,则选取它的概率为m/n * (m-1)/(n-1)*....1/(n-m+1)=1/C(n,m),可以看到概率是相等的。
Knuth 老爷爷很早就提出了这个算法,他的实现如下:
void randomMKnuth(int n, int m)
{int i;for (i = 0; i < n; i++) {if ((rand() % (n-i)) < m) {printf("%d ", i);m--;}}
}
解2: 还可以采用前面随机排列数组的思想,先对前 m 个数字进行随机排列,然后排序这 m 个数字并输出即可。代码如下:
void randomMArray(int n, int m)
{int i, j;int *x = (int *)malloc(sizeof(int) * n);for (i = 0; i < n; i++)x[i] = i;// 随机数组for (i = 0; i < m; i++) {j = randInt(i, n-1);swapInt(x, i, j);}// 对数组前 m 个元素排序for (i = 0; i < m; i++) {for (j = i+1; j>0 && x[j-1]>x[j]; j--) {swapInt(x, j, j-1);}}for (i = 0; i < m; i++) {printf("%d ", x[i]);}printf("\n");
}
4 rand7 生成 rand10 问题
题: 已知一个函数rand7()能够生成1-7的随机数,每个数概率相等,请给出一个函数rand10(),该函数能够生成 1-10 的随机数,每个数概率相等。
解1: 要产生 1-10 的随机数,我们要么执行 rand7() 两次,要么直接乘以一个数字来得到我们想要的范围值。如下面公式(1)和(2)。
idx = 7 * (rand7()-1) + rand7() ---(1) 正确
idx = 8 * rand7() - 7 ---(2) 错误
上面公式 (1) 能够产生 1-49 的随机数,为什么呢?因为 rand7() 的可能的值为 1-7,两个 rand7() 则可能产生 49 种组合,且正好是 1-49 这 49 个数,每个数出现的概率为 1/49,于是我们可以将大于 40 的丢弃,然后取 (idx-1) % 10 + 1 即可。公式(2)是错误的,因为它生成的数的概率不均等,而且也无法生成49个数字。
1 2 3 4 5 6 7
1 1 2 3 4 5 6 7
2 8 9 10 1 2 3 4
3 5 6 7 8 9 10 1
4 2 3 4 5 6 7 8
5 9 10 1 2 3 4 5
6 6 7 8 9 10 * *
7 * * * * * * *
该解法基于一种叫做拒绝采样的方法。主要思想是只要产生一个目标范围内的随机数,则直接返回。如果产生的随机数不在目标范围内,则丢弃该值,重新取样。由于目标范围内的数字被选中的概率相等,这样一个均匀的分布生成了。代码如下:
int rand7ToRand10Sample() {int row, col, idx;do {row = rand7();col = rand7();idx = col + (row-1)*7;} while (idx > 40);return 1 + (idx-1) % 10;
}
由于row范围为1-7,col范围为1-7,这样idx值范围为1-49。大于40的值被丢弃,这样剩下1-40范围内的数字,通过取模返回。下面计算一下得到一个满足1-40范围的数需要进行取样的次数的期望值:
E(# calls to rand7) = 2 * (40/49) +4 * (9/49) * (40/49) +6 * (9/49)2 * (40/49) +...∞= ∑ 2k * (9/49)k-1 * (40/49)k=1= (80/49) / (1 - 9/49)2= 2.45
解2: 上面的方法大概需要2.45次调用 rand7 函数才能得到 1 个 1-10 范围的数,下面可以进行再度优化。对于大于40的数,我们不必马上丢弃,可以对 41-49 的数减去 40 可得到 1-9 的随机数,而rand7可生成 1-7 的随机数,这样可以生成 1-63 的随机数。对于 1-60 我们可以直接返回,而 61-63 则丢弃,这样需要丢弃的数只有3个,相比前面的9个,效率有所提高。而对于61-63的数,减去60后为 1-3,rand7 产生 1-7,这样可以再度利用产生 1-21 的数,对于 1-20 我们则直接返回,对于 21 则丢弃。这时,丢弃的数就只有1个了,优化又进一步。当然这里面对rand7的调用次数也是增加了的。代码如下,优化后的期望大概是 2.2123。
int rand7ToRand10UtilizeSample() {int a, b, idx;while (1) {a = randInt(1, 7);b = randInt(1, 7);idx = b + (a-1)*7;if (idx <= 40)return 1 + (idx-1)%10;a = idx-40;b = randInt(1, 7);// get uniform dist from 1 - 63idx = b + (a-1)*7;if (idx <= 60)return 1 + (idx-1)%10;a = idx-60;b = randInt(1, 7);// get uniform dist from 1-21idx = b + (a-1)*7;if (idx <= 20)return 1 + (idx-1)%10;}
}
5 趣味概率题
1)称球问题
题: 有12个小球,其中一个是坏球。给你一架天平,需要你用最少的称次数来确定哪个小球是坏的,并且它到底是轻了还是重了。
解: 之前有总结过二分查找算法,我们知道二分法可以加快有序数组的查找。相似的,比如在数字游戏中,如果要你猜一个介于 1-64 之间的数字,用二分法在6次内肯定能猜出来。但是称球问题却不同。称球问题这里 12 个小球,坏球可能是其中任意一个,这就有 12 种可能性。而坏球可能是重了或者轻了这2种情况,于是这个问题一共有 12*2 = 24 种可能性。每次用天平称,天平可以输出的是 平衡、左重、右重 3 种可能性,即称一次可以将问题可能性缩小到原来的 1/3,则一共 24 种可能性可以在 3 次内称出来(3^3 = 27)。
为什么最直观的称法 6-6 不是最优的?在 6-6 称的时候,天平平衡的可能性是0,而最优策略应该是让天平每次称量时的概率均等,这样才能三等分答案的所有可能性。
具体怎么实施呢? 将球编号为1-12,采用 4, 4 称的方法。
- 我们先将
1 2 3 4和5 6 7 8进行第1次称重。 - 如果第1次平衡,则坏球肯定在
9-12号中。则此时只剩下9-124个球,可能性为9- 10- 11- 12- 9+ 10+ 11+ 12+这8种可能。接下来将9 10 11和1 2 3称第2次:如果平衡,则12号小球为坏球,将12号小球与1号小球称第3次即可确认轻还是重。如果不平衡,则如果重了说明坏球重了,继续将9和10号球称量,重的为坏球,平衡的话则11为坏球。 - 如果第1次不平衡,则坏球肯定在
1-8号中。则还剩下的可能性是1+ 2+ 3+ 4+ 5- 6- 7- 8-或者1- 2- 3- 4- 5+ 6+ 7+ 8+,如果是1 2 3 4这边重,则可以将1 2 6和3 4 5称,如果平衡,则必然是7 8轻了,再称一次7和1,便可以判断7和8哪个是坏球了。如果不平衡,假定是1 2 6这边重,则可以判断出1 2重了或者5轻了,为什么呢?因为如果是3+ 4+ 6-,则1 2 3 4比5 6 7 8重,但是1 2 6应该比3 4 5轻。其他情况同理,最多3次即可找出坏球。
下面这个图更加清晰说明了这个原理。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NecW12n8-1682522423467)(null)]
2)生男生女问题
题: 在重男轻女的国家里,男女的比例是多少?在一个重男轻女的国家里,每个家庭都想生男孩,如果他们生的孩子是女孩,就再生一个,直到生下的是男孩为止。这样的国家,男女比例会是多少?
解: 还是1:1。在所有出生的第一个小孩中,男女比例是1:1;在所有出生的第二个小孩中,男女比例是1:1;… 在所有出生的第n个小孩中,男女比例还是1:1。所以总的男女比例是1:1。
3)约会问题
题: 两人相约5点到6点在某地会面,先到者等20分钟后离去,求这两人能够会面的概率。
解: 设两人分别在5点X分和5点Y分到达目的地,则他们能够会面的条件是 |X-Y| <= 20,而整个范围为 S={(x, y): 0 =< x <= 60, 0=< y <= 60},如果画出坐标轴的话,会面的情况为坐标轴中表示的面积,概率为 (60^2 - 40^2) / 60^2 = 5/9。
4)帽子问题
题: 有n位顾客,他们每个人给餐厅的服务生一顶帽子,服务生以随机的顺序归还给顾客,请问拿到自己帽子的顾客的期望数是多少?
解: 使用指示随机变量来求解这个问题会简单些。定义一个随机变量X等于能够拿到自己帽子的顾客数目,我们要计算的是 E[X]。对于 i=1, 2 ... n,定义 Xi =I {顾客i拿到自己的帽子},则 X=X1+X2+…Xn。由于归还帽子的顺序是随机的,所以每个顾客拿到自己帽子的概率为1/n,即 Pr(Xi=1)=1/n,从而 E(Xi)=1/n,所以E(X)=E(X1 + X2 + …Xn)= E(X1)+E(X2)+…E(Xn)=n*1/n = 1,即大约有1个顾客可以拿到自己的帽子。
5)生日悖论
题: 一个房间至少要有多少人,才能使得有两个人的生日在同一天?
解: 对房间k个人中的每一对(i, j)定义指示器变量 Xij = {i与j生日在同一天} ,则i与j生日相同时,Xij=1,否则 Xij=0。两个人在同一天生日的概率 Pr(Xij=1)=1/n 。则用X表示同一天生日的两人对的数目,则 E(X)=E(∑ki=1∑kj=i+1Xij) = C(k,2)*1/n = k(k-1)/2n,令 k(k-1)/2n >=1,可得到 k>=28,即至少要有 28 个人,才能期望两个人的生日在同一天。
6)概率逆推问题
题: 如果在高速公路上30分钟内看到一辆车开过的几率是0.95,那么在10分钟内看到一辆车开过的几率是多少?(假设常概率条件下)
解: 假设10分钟内看到一辆车开过的概率是x,那么没有看到车开过的概率就是1-x,30分钟没有看到车开过的概率是 (1-x)^3,也就是 0.05。所以得到方程 (1-x)^3 = 0.05 ,解方程得到 x 大约是 0.63。
相关文章:

# 数据结构和算法面试题系列-随机算法总结
0 概述 随机算法涉及大量概率论知识,有时候难得去仔细看推导过程,当然能够完全了解推导的过程自然是有好处的,如果不了解推导过程,至少记住结论也是必要的。本文总结最常见的一些随机算法的题目,是几年前找工作的时候…...

windows中vscode配置C/C++环境
首先要把MinGW的环境安装完,我一般是下载带有MinGW的codeblocks,这样省去自己安装MinGW。因为安装MinGW还挺麻烦的。 安装完codeblocks,找到其安装目录,把bin文件配置到环境变量去: 将bin添加到环境变量 然后打开vsco…...
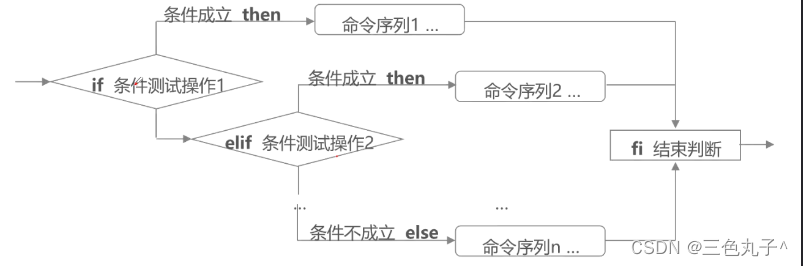
shell编程之条件语句
shell编程之条件语句 一、条件测试操作1.test命令2.文件测试3.利用条件判断,创建文件4.整数值比较4.1 常用的测试操作符 5.字符串比较5.1 常用的测试操作符 6.逻辑测试6.1 常用的测试操作符 二、if语句的结构1.单分支结构2.双分支结构3.多分支结构4.if嵌套 三、case…...

【Python每日十题菜鸟版--第二天】
菜鸟实例 🍉前言1.判断奇偶性2.判断闰年3. 获取最大值最小值4. 质数(素数)的判断5.阶乘方法一方法二 6.九九乘法表7.斐波那契数列方法一 :循环计算法(一般方法)方法二: 递归 8.阿姆斯特朗数9. 十…...
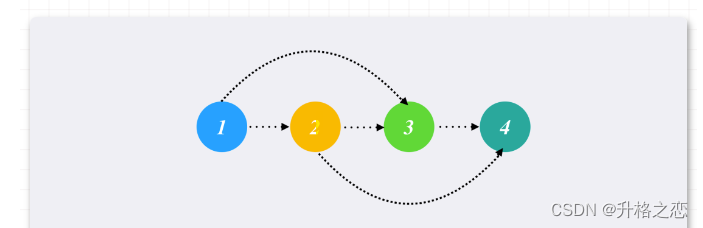
拓扑排序模板及例题
概念 一个有向无环图必然存在一个拓扑序列与之对应。 流程: 先将所有入度为0的节点入队将队列中的节点出队,出队序列就是对应拓扑序。对于弹出的节点x,遍历x所有出度y,对y进行入读减一操作检查入度减一之后的节点y,…...

linux查看nginx安装路径
linux查看nginx安装路径 有几种方法可以查看nginx的安装路径: 使用which命令: which nginx这个命令会返回nginx的二进制文件路径,一般也是安装路径。 查看nginx的进程,得到安装路径: ps aux | grep nginx输出结果中有nginx的进程路径,这个也是安装路径。 在nginx的配置文…...

【生态环境保护】绿水青山就是金山银山——生态环保篇
环保是一个持续性的话题,不仅仅是在国内,整个世界都是一个命运共同体从城市垃圾分类,到农村/村镇污水治理,城乡一体化和因地制宜的实施方式,是我们一直在探索的。 从余村到全国,从中国到世界,“…...
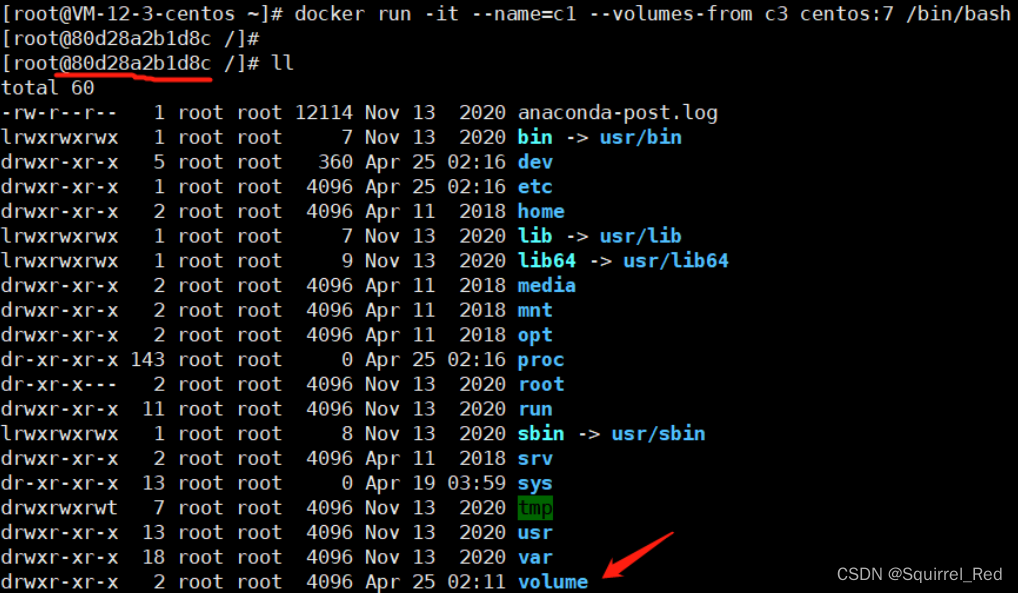
配置Docker镜像加速器-Docker命令-Docker 容器的数据卷
Docker架构 docker进程(daemon) 镜像(Image):Docker 镜像(Image),就相当于是一个 root 文件系统。比如官方镜像 ubuntu:16.04 就包含了完整的一套 Ubuntu16.04 最小系统的 root 文件…...

ARM开发调试方法
用户选用ARM处理器开发嵌入式系统时,选择合适的开发工具可以加快开发进度,节省开发成本。因此一套含有编辑软件、编译软件、汇编软件、链接软件、调试软件、工程管理及函数库的集成开发环境(IDE)一般来说是必不可少的,…...
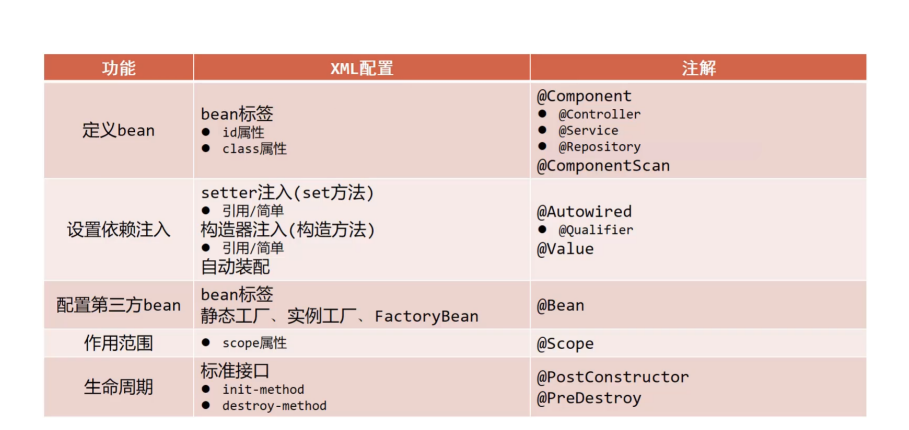
【Spring篇】IOC/DI注解开发
🍓系列专栏:Spring系列专栏 🍉个人主页:个人主页 目录 一、IOC/DI注解开发 1.注解开发定义bean 2.纯注解开发模式 1.思路分析 2.实现步骤 3.注解开发bean作用范围与生命周期管理 1.环境准备 2.Bean的作用范围 3.Bean的生命周期 4.注解开发依赖…...

1 Unix基础知识
1.1 登录 1.1 登录名 登录Unix系统时,要先输入登录名,然后再输入口令。系统再其口令文件(/etc/password文件)查看登录名。口令文件中的登录项由7个以冒号分隔的字段组成:登录名,加密口令,数字用…...

【翻译一下官方文档】认识uniCloud云数据库(基础篇)
我将用图文的形式,把市面上优质的课程加以自己的理解,详细的把:创建一个uniCloud的应用,其中的每一步记录出来,方便大家写项目中,做到哪一步不会了,可以轻松翻看文章进行查阅。(此文…...

全局解释器锁 GIL
问题 你已经听说过全局解释器锁 GIL,担心它会影响到多线程程序的执行性能。 解决方案 尽管 Python 完全支持多线程编程,但是解释器的 C 语言实现部分在完全并行执行时并不是线程安全的。 实际上,解释器被一个全局解释器锁保护着ÿ…...

github 下载文件加速 https://moeyy.cn/gh-proxy/
GitHub文件链接带不带协议头都可以,支持release、archive以及文件,右键复制出来的链接都是符合标准的。 注意,不支持项目文件夹,请使用Git。 分支源码:https://github.moeyy.xyz/https://github.com/moeyy/project/arc…...
第五章 资源包使用
游戏开发中会大量使用模型文件,图片文件,这些资源都需要事先导入到项目中去。导入的方式非常简单,将这些文件直接复制到项目中的Assets目录下即可。Unity 会在文件添加到 Assets 文件夹时自动检测到这些文件并同步显示在Project视图中。 Uni…...

Linux od命令
Linux od命令用于输出文件内容。 od指令会读取所给予的文件的内容,并将其内容以八进制字码呈现出来。 语法 od [-abcdfhilovx][-A <字码基数>][-j <字符数目>][-N <字符数目>][-s <字符串字符数>][-t <输出格式>][-w <每列字符…...

【15】SCI易中期刊推荐——电子电气 | 仪器仪表(中科院4区)
💖💖>>>加勒比海带<<<💖💖 🍀🍀>>>【YOLO魔法搭配&论文投稿咨询】<<<🍀🍀 ✨✨>>>学习交流 | 温澜潮生 | 合作共赢 | 共同进步<<<✨✨ 📚📚>>>人工智能 | 计算机视觉 | 深度学习Tr…...

基于PaddleServing的串联部署 ocr 识别模型
要点: 使用paddleserving服务 1 首先需要安装PaddleServing部署相关的环境 PaddleServing是PaddlePaddle推出的一种高性能、易扩展、高可用的机器学习服务框架。PaddleOCR中使用PaddleServing主要是为了将训练好的OCR模型部署到线上环境,提供API服务&a…...

java OutputStream学习
1.概要 OutputStream位于java.io,它在Java 实现的IO类库中是一个很基础的抽象类。在层级上,是所有字节输出流类的父类,在功能上,表示接受字节并把它们输出。 2.实现类及子类简介 OutputStream有诸多子类: ByteAr…...

java 上传文件生成二进制流文件
最近在项目中遇到一个问题:需要将上传的文件生成输出流,然后将输出流转换为输入流上传到oss。 -------------------------------------------导出代码实现---------------------------------------------------------- ByteArrayOutputStream baos nu…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
